Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Validation des principes de la relativité restreinte - Relativité restreinte (3/3)
03/07/2012
Article produit lors d'une conférence sur la « Relativité restreinte » dans le cadre d'une formation organisée par la section locale de l'Udppc de Lyon .
Cette formation était adressée aux professeurs de Sciences physiques et chimiques pour approfondir les notions du nouveau programme de terminale, 13 juin 2012
Résumé
Cet article présente les expériences qui ont permis de valider les principes de la relativité restreinte décrit par Einstein précédemment.
Table des matières
- I. Validations expérimentales
- a. Expérience de Frisch et Smith 1963 : désintégration des muons atmosphériques
- b. Expérience des horloges embarquées de Hafele et Keating en 1971
- c. Effet Doppler relativiste : « redshift » en astrophysique
- d. Expérience interférentielle de Fizeau en 1851 : la lumière n'obéit pas à la règle habituelle de la mécanique newtonienne de composition des vitesses
- e. Aberration des étoiles
- II. Prolongements : la recherche des invariants
- Conclusion générale
I. Validations expérimentales
L'effet relativiste de variations des durées est d'autant plus important que la vitesse V des référentiels est grande. C'est dans le domaine des particules qui approchent la vitesse de la lumière que les effets relativistes seront les plus spectaculaires.
En physique des particules, les grandeurs sont toujours décrites dans le référentiel de repos des particules massives, notamment la durée de vie dite propre. Ces particules instables peuvent être considérées comme des horloges naturelles, et donc être utilisées pour tester la dilatation des durées.
Le seul référentiel privilégié à introduire est le référentiel propre noté (R0) d'une particule, qui par définition est au repos dans ce référentiel.
Dans le cas d'une expérience relevant de la cinématique, on considère classiquement deux événements E1 et E2 :
- événement E1 : émission ou création de la particule P
- événement E2 : disparition ou désintégration de cette particule.
a. Expérience de Frisch et Smith 1963 : désintégration des muons atmosphériques
Une horloge « parfaite » est une horloge dont le fonctionnement est très peu (à la limite nullement) affecté par les forces de gravitation et d'inertie. La meilleure approximation de l'horloge parfaite réalisée à ce jour est l'horloge atomique ou plutôt nucléaire. Dans les conditions ordinaires les forces d'inertie sont négligeables devant les forces électriques et à fortiori devant les forces nucléaires qui déterminent, les unes, les processus dans les couches électroniques, les autres, les processus dans les noyaux des atomes.
L'effet de « dilatation des durées » a aussi été mis en évidence en recueillant au niveau du sol des particules appelées muons (aussi appelées « électrons lourds » ; 207 fois la masse de l'électron), d'énergie 100 Gev, qui sont produits dans la haute atmosphère par la désintégration de « mésons π » issus de l'interaction de protons de très haute énergie (rayons cosmiques) avec les particules atmosphérique, ce qui constitue l'événement (A).
Voir l'animation sur l'expérience des muons
Ils se désintègrent en donnant un électron, un neutrino muonique et un antineutrino électronique) :
Cette désintégration des muons (qui constitue l'événement (B)) s'effectue selon une loi exponentielle (réaction du premier ordre : la diminution par désintégration du nombre de particules d'une quantité dn durant la durée dt, entre t et t + dt est directement proportionnelle au nombre n(t) de particules présentes à l'instant t) :
où n(t) est le nombre de muons à l'instant t, τ une constante appelée durée de vie des muons.
La mesure au laboratoire du nombre de désintégrations des muons au repos permet de tracer n(t). Puisque dans cette expérience les particules qui se désintègrent sont au repos, on note τ0 leur durée de vie moyenne mesurée dans le référentiel du laboratoire. On trouve aisément τ0 = 2,2.10-6s (à partir de la pente à l'origine du graphe de n(t)). La vitesse des muons est de l'ordre de la vitesse de la lumière (99,52% soit 298 000 km.s-1), leur libre parcours moyen devrait alors être de cτ0, soit 660 m.
En physique classique cela signifierait que le nombre de muons détectés par heure est divisé par e = 2,71 tous les 660 m.
Des compteurs à scintillations, placés sur une montagne à différentes altitudes, permettent de dénombrer les muons cosmiques qui proviennent de la haute atmosphère.
Dans l'expérience réelle de mesure, ce ne sont pas les mêmes muons qui sont détectés entre deux altitudes différentes, les emplacements des détecteurs n'étant pas situés sur une même verticale. Cependant, les mesures montrent que l'intensité des rayons cosmiques ne varie pas d'un instant à l'autre ni d'un endroit à l'autre, tout au moins pour les distances considérées. Les mesures sont donc identiques à celles qu'on effectuerait sur un même groupe de muons.
Le scintillateur est traversé sans difficulté par la plupart des muons ; certains (moins de 1%), freinés par le bloc de métal placé au-dessus (75 cm d'épaisseur de fer), sont stoppés au niveau du scintillateur. Le passage ou l'arrivée d'un muon dure un temps très court (moins de 1.10-9s) et se traduit par un éclair lumineux, qui est enregistré sous forme d'une impulsion sur un écran d'oscilloscope, via un photomultiplicateur. Un muon arrêté dans le scintillateur a toutes les chances de se désintégrer dans les quelques microsecondes suivant son arrivée ; l'électron énergique qui en résulte donne une seconde impulsion séparées de Δt. En faisant la statistique de ces durées Δt, on peut vérifier la loi de décroissance exponentielle.
L'expérience a été réalisée par B. Rossi et D.B. Hall en 1941 sur un dénivellé de 1624 m entre Echo Lake (3240 m) et Denver (1616 m), puis par D.H. Frisch et J.H. Smith en 1963 entre le sommet du Mont Washington (1907 m) et le niveau de la mer.
Ces derniers ont dénombré 568 ± 10 muons par heure à une altitude de 2000 m, alors qu'au niveau de la mer on n'en dénombre plus que 412 ± 9 par heure. - En raisonnant en mécanique galiléenne, il faut une durée de : soit Le résultat s'écarte d'un facteur 15 de la valeur expérimentale. - Les muons sont en translation par rapport au référentiel terrestre, Leur durée de vie moyenne au repos doit être remplacée par celle perçue par l'observateur en mouvement par rapport aux muons soit en utilisant la Relativité Restreinte : On obtient donc : |
La valeur obtenue par la théorie relativiste est proche des données expérimentales. On obtient ainsi une vérification par l'expérience de la relativité du temps. Les muons se déplaçant tellement vite, la montagne leur paraît 15 fois moins haute qu'à un observateur placé sur la Terre.
Cette expérience sur les muons est très instructive. Elle confirme trois prédictions relativistes : le ralentissement des horloges, la contraction des longueurs et le comportement relativiste identique de tous les types d'horloges. De plus, la relativité s'applique ici à un phénomène – la désintégration des muons - qui n'est ni mécanique ni électromagnétique.
b. Expérience des horloges embarquées de Hafele et Keating en 1971
Une vérification expérimentale de la dilatation des durées fut effectuée en 1971. Deux avions à bord desquels une horloge atomique au césium avait été placée effectuèrent leurs vols commerciaux régulier à la même vitesse et dans des directions différentes, l'un vers l'est et l'autre vers l'ouest. Puis ils comparèrent leur horloge atomique à une troisième horloge atomique au sol.
L'avion volant vers l'est perdit δtE = - 59 ns alors que l'avion volant vers l'ouest gagna δtO = + 273 ns. Deux effets sont présents :
- les horloges mobiles « ralentissent »,
- mais un effet de Relativité Générale les « accélère » plutôt ; cependant la différence des durées de parcours est moins sensible à l'effet de Relativité Générale (qui se compensent).
Soit cet écart : Δ = δtE - δt0 = - 59 - (+273) = - 332 ± 17 ns
Analysons l'expérience, en supposant que tous les référentiels sont galiléens. On considère trois référentiels galiléens, un situé au Pôle Nord, un sur Terre et un dans l'avion. Les intervalles de temps δtN, δtT et δtA par rapport à chaque référentiel respectivement, sont reliés entre eux par les lois : On suppose que les deux avions ont des vitesses de croisière constante par rapport au sol VC (le référentiel terrestre). La vitesse de chaque avion (non relativiste) est donc : Comme les vitesses sont petites par rapport à celle de la lumière, on peut linéariser les lois précédentes, on obtient : ce qui est cohérent avec le signe trouvé expérimentalement. On peut estimer la vitesse de croisière, en connaissant R le rayon de l'orbite de l'avion par rapport à la Terre, c'est-à-dire le parcours relativement au référentiel géocentrique soit : De même la vitesse du référentiel lié à la Terre est de : D'où : avec Vc = 220 m.s-1 et la durée du voyage δtT = 45 h. |
Résultat tout à fait cohérent. Les écarts s'expliquent assez bien par des durées de vol différentes, des altitudes variables, des trajectoires approximatives, ou par l'imprécision des horloges à l'époque.
c. Effet Doppler relativiste : « redshift » en astrophysique
Au phénomène de Doppler classique, étudié en optique par Fizeau, se superpose le phénomène de relativité du temps quand la source est en mouvement à très grande vitesse : c'est l'effet Doppler-Fizeau relativiste (combinaison d'un effet Doppler classique avec une vitesse radiale et un « ralentissement » des horloges mobiles).
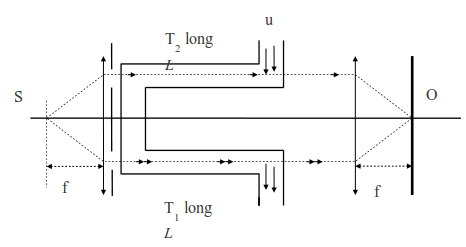
L'atome est considéré comme une source de lumière monochromatique de période propre T0, assimilé à un oscillateur harmonique qui, dans son référentiel propre (R0), possède une fréquence υ0, correspondant à une transition radiative. Dans le référentiel du laboratoire (R), cette fréquence vaut υ.
Les deux événements entre lesquels on mesure la distance spatio-temporelle, seront respectivement le début E1 et la fin E2 de N oscillations (éclairs) exactement (on peut bien sûr faire le raisonnement pour N = 1) dans un point-de vue ondulatoire. C'est une simple commodité de langage de parler de l'atome comme d'un observateur galiléen muni d'une horloge.
D'un point de vue corpusculaire, on pourrait aussi considérer les deux événements comme la création puis disparition d'un photon (particule de masse nulle et vitesse c dans tous les référentiels !).
Dans la théorie classique de l'effet Doppler l'écart de fréquence ne dépend, au premier ordre, que de la vitesse relative de la source émettrice par rapport au récepteur. En Relativité la propagation de la lumière est isotrope dans tous les référentiels galiléens ; nous pouvons faire les calculs dans n'importe lequel d'entre eux, le plus simple, par exemple, est de se placer dans le référentiel associée à la source S, prise comme origine du repère (R). Soit un observateur O' animé d'un mouvement rectiligne uniforme selon Sx, avec une vitesse V > 0 (s'éloigne de la source).
A l'instant t (heure de S dans (R)), il y a émission d'un premier éclair (top). A t + T0 il y a émission d'un second éclair (période d'émission), tandis que le premier top a parcouru vers O' la distance d1 = cT0 = λ0 qu'on peut appeler sans ambiguïté la longueur d'onde propre de la source. Les deux fronts d'onde, séparés de λ0, se propagent à la vitesse c vers O', qui reçoit le premier éclair à t1 (heure de (R)). O' reçoit le second éclair à t1 + Δt tel que :
soit Nous sommes prévenus que t, t1 et Δt sont des temps mesurés dans (R) avec des horloges synchronisées mobiles par rapport à l'observateur. La Relativité intervient quand on demande quel est pour l'observateur O' l'intervalle de temps T' entre les deux événements : réception du premier éclair et du second éclair. T' est une durée propre (mesurée par une même horloge). Nous savons qu'il y a la relation de dilatation : ou ou Pour V << c, un développement au second ordre donne : qui diffère du développement classique. L'exactitude du terme du second ordre de la loi relativiste a été vérifiée par Ives et Stillwell, en 1938, avec un faisceau de rayons composés d'atomes d'hydrogène ionisés H2+ à grande vitesse (V = 0,005 c). |
La lumière émise par le faisceau dans la direction de la vitesse, en avant (λ'1) et en arrière (λ'2), après réflexion sur un miroir, était analysée par un spectrographe. Ils ont observé un déplacement spectral de la raie Hβ :
qu'on peut estimer au second ordre ,
λ0 = 486,0 nm, mesure en Angstrom.
0,067 | 0,0670 |
0,090 | 0,0869 |
0,0995 | 0,1049 |
0,1098 | 0,1098 |
On parle d'effet Doppler longitudinal.
Quand la source s'éloigne de l'observateur, le décalage du spectre a lieu vers les grandes longueurs d'onde. On dit qu'on observe un « déplacement vers le rouge » ou « redshift » en anglais (λ' > λ).
Les astronomes ont découvert depuis 1960, des sources baptisées quasars (quasi-stellar) dont la particularité est d‘avoir de très forts déplacements vers le rouge (de l'ordre de 2 !). Ainsi la raie Lyman alpha de l'hydrogène (λ0 = 121,6 nm) qui se trouve « normalement » dans l'ultraviolet lointain, se retrouve dans le spectre visible (λ' = 364,8 nm). On conçoit que l'identification de telles raies est très difficile (V = 0,8 c).
Les mesures effectuées par les astrophysiciens montrent que le rayonnement émis par chaque amas de galaxies subit un tel déplacement, justifiant ainsi que tous ces amas s'éloignent de notre référentiel terrestre. C'est une preuve indirecte de l'expansion de l'Univers et par suite du Big-Bang.
Remarque
Il existe aussi un effet Doppler transversal purement relativiste associé au ralentissement de la marche d'une horloge en mouvement quand l'observation se fait perpendiculairement à la direction de l'onde qui se propage, on a la relation :
effet du second ordre en V/c (plus difficile à observer).
Il a été observé pour la première fois en 1938-41 par Ives et Stillwell avec un faisceau de rayons composés d'atomes d'hydrogène à grande vitesse. La lumière émise perpendiculairement au faisceau était analysée par un spectrographe.
Ils ont observé un déplacement spectral de la raie Hβ de 2 pm pour les ions H2+ de longueur d'onde 486,0 nm.
d. Expérience interférentielle de Fizeau en 1851 : la lumière n'obéit pas à la règle habituelle de la mécanique newtonienne de composition des vitesses
On considère le dispositif expérimental de Fizeau schématisé ci-contre.
On place une source ponctuelle en S. Les fentes F1 et F2 sont très fines. Les tubes ont même longueur L. Les axes parallèles, contiennent un même liquide d'indice n.
Quand le liquide est au repos dans T1 et T2, on observe une frange centrale brillante au foyer O de la lentille L2. Le liquide est mis en mouvement aux vitesses + u et – u respectivement.
On observe une modification de la figure d'interférence.
Soient V1 et V2 la vitesse de la lumière dans les tubes T1 et T2 respectivement. L'allure de la figure d'interférence en O peut se déduire des deux quantités que sont la différence des durées des parcours des deux ondes qui interfèrent en O, ΔT, et de la différence de chemin optique entre les deux ondes en O, δ : , Le calcul des vitesses est différent en physique classique et en physique relativiste ; - classique : , - relativiste (obtenu à partir des transformations de Poincaré-Lorentz) : , Le nombre de franges brillantes qui défilent est donné par : et . Les résultats expérimentaux avec n = 4/3, u = 7 m.s-1, λ = 540 nm, L = 1,5 m confirment l'expression relativiste. |
e. Aberration des étoiles
L'astronome anglais J.Bradley (1693-1762) cherchait à mesurer la distance des étoiles au Soleil ou plus précisément leurs « parallaxes ». La parallaxe d'une étoile est l'angle A sous lequel on verrait le rayon de l'orbite terrestre à partir de l'étoile. Pour mesurer cet angle il « suffit » d'observer l'étoile tout au long de l'année et de remarquer que la direction d'observation va varier. | 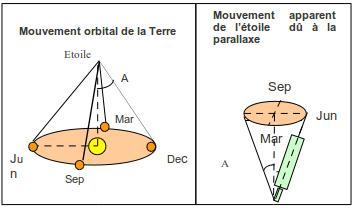 |
En considérant, pour simplifier, une étoile dans une direction perpendiculaire au plan de la trajectoire de la Terre autour du Soleil, on remarque que la direction de la lunette d'observation décrit un cône dont le demi-angle au sommet est égal à la parallaxe A. A priori la parallaxe d'une telle étoile dépend de sa distance au soleil et elle est d'autant plus faible que l'étoile est plus éloignée. | 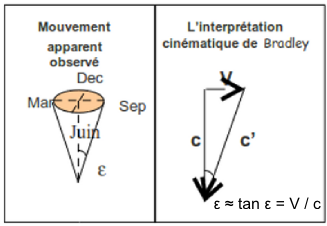 |
Les observations de Bradley sont différentes. D'une part la direction apparente d'observation varie d'une manière différente au cours de l'année et d'autre part, le mouvement apparent de l'étoile est un mouvement circulaire dont le rayon angulaire ε est égal à 20'' d'angle (diamètre apparent d'un cheveu tenu à bout de bras) et ceci quelle que soit l'étoile observée !
L'interprétation donnée par Bradley est de nature « cinématique » et résulte de la composition des vitesses de la lumière et de la Terre par rapport au référentiel « héliocentrique » lié au Soleil : l'observateur « voit » l'étoile dans la direction de la vitesse relative c' = c – V. | 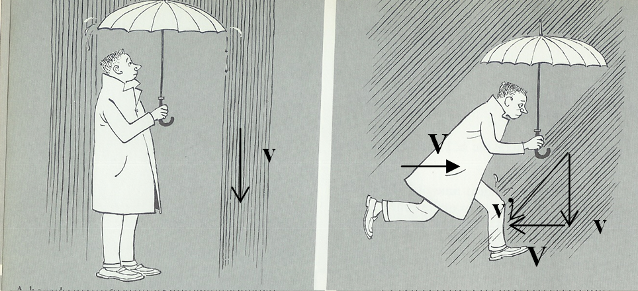 |
Connaissant l'angle d'aberration ε, Bradley a ainsi estimé la vitesse de la lumière à environ 10 000 fois la vitesse orbitale de la Terre, soit environ 300 000 km.s-1.
Dans le cas de l'observation de Bradley l'une des vitesses à composer est celle de la lumière et l'addition classique n'est plus a priori applicable ! Néanmoins comme V << c la cinématique relativiste conduit à un résultat identique si on limite la précision des calculs au premier ordre en V/c.
Notons que l'effet d'aberration de la lumière n'a aucun rapport avec la vitesse de déplacement des étoiles par rapport à la Terre, et ne fait que refléter la variation de la vitesse de ce mouvement relatif, déterminée par le mouvement de la Terre. C'est pour cela que l'aberration est la même pour toutes les étoiles, bien que leurs vitesses par rapport à la Terre soient très différentes.
II. Prolongements : la recherche des invariants
a. L'invariant cinématique
Pour la mécanique newtonienne, l'intervalle de temps entre deux événements observés dans deux référentiels (R) et (R') est un invariant vis à vis d'un changement de référentiel :
(i)
Il en découle une chronologie universelle et les lois de transformation des vitesses et des accélérations, en particulier dans le cas présent où les référentiels sont en translation rectiligne uniforme l'un par rapport à l'autre (vitesse u d'un point lié à (R') par rapport à (R)). On a :
(ii)
L'expérience est en accord avec l'invariant (i) et la loi de composition des vitesses (ii) tant que toutes les vitesses en question sont petites devant la vitesse de la lumière dans le vide. Par contre l'expérience est en désaccord dans le cas contraire.
D'après le second postulat d'Einstein on doit poser que la vitesse du photon a la même valeur, soit c, par rapport à tous les référentiels.
On peut écrire cela : quel que soit le référentiel, pour un photon.
On peut généraliser ce résultat à une particule P quelconque.
La Relativité Restreinte pose comme nouvel invariant :
avec (R0) le référentiel propre de la particule.
b. Conséquences
Durée de vie d'une particule qui se désintègre, ou la dilatation des durées propres :
Dans le référentiel propre (R0), est sa durée de vie moyenne propre.
Dans le référentiel (R) où elle possède la vitesse V, elle parcourt pendant sa durée de vie « de vol » τ.
On a donc : soit
Transformations de Poincaré-Lorentz
On déduit de cet invariant cinématique, sans calculs laborieux, les relations de transformation de Lorentz-Poincaré , avec (R') en translation rectiligne uniforme par rapport à (R) avec la vitesse V selon 0x.
Considérons deux événements E1 et E2 situés selon l'axe Ox.
L'événement E1 est repéré dans (R), par x1 = 0, t1 = 0 ; dans (R'), x'1 = 0, t'1 = 0.
L'événement E2 est repéré dans (R), par x2, t2 ; dans (R'), x'2, t'2.
On note les distances et durées ; x = x2 – x1, x' = x'2 – x'1, t = t2 - t1, t' = t'2 - t'1.
L'invariant cinématique permet d'écrire : avec y' = y, z' = z. On doit traiter x (ou x') et ct (ou ct') symétriquement ; x' et t' doivent avoir une relation linéaire en x et t. Posons en reportant dans l'invariant, par identification des termes en ct et x2 on trouve les coefficients : D'où la transformation de FitzGerald-Poincaré-Lorentz : |
On voit que la relation de composition des vitesses galiléennes est modifiée quand la vitesse des objets matériels est très grande.
Notons que les transformations de Lorentz peuvent être retrouvées à partir du principe de relativité et de considérations d'isotropie (ne dépendant pas de la direction de l'espace) et d'homogénéité (ne dépendant pas de la position dans l'espace) de l'espace et du temps. (cf J.-M. Levy-Leblond).
La théorie de la Relativité Restreinte peut ainsi être formulée de façons différentes selon le choix des axiomes de départ.
La simultanéité en Relativité
Soient deux événements simultanés dans (R), par définition : t1 = t2.
On peut calculer la durée qui sépare les évènements dans le référentiel (R'), en nous servant de la transformation de Poincaré - Lorentz :
Ainsi deux événements simultanés dans (R) ne le sont pas nécessairement dans (R').
Il est intéressant de remarquer que l'on retrouve la conception classique dans le cas limite où c est infiniment grand.
La contraction des longueurs (propres)
Soient A' et B' deux points rigidement liés au référentiel (R'), il s'agit d'une règle par exemple posée selon l'axe 0x. La règle se déplace selon l‘axe Ox à une vitesse constante V. Les observateurs de (R') ont tout le temps de constater la coïncidence (prolongée) entre les points A' et B' ; la longueur L0 = A'B' de la règle mesurée dans son référentiel (R') est ce qu'on appelle la longueur propre.
Notre problème est de savoir comment les observateurs de (R) peuvent mesurer la longueur L de la règle mobile A'B'.
Une méthode toute naturelle est de constater, à un même instant t, la coïncidence (momentanée) de A' et B' avec les traits M et N d'une règle de (R) ; la longueur L de la règle dans (R), à l'instant t, est la distance MN entre les positions instantanées (à cet instant t) des deux extrémités A', B' de la règle.
Dans (R'), on note : A'(x'1), et B'(x'2), les extrémités de la règle de longueur propre L0 = x'2 – x'1.
Dans (R), les horloges distribuées selon l'axe Ox ont été synchronisées avant le passage de la règle. L'observateur M(x1) a noté le passage de l'extrémité A' à t = 3 (événement E1) et c'est l'observateur N(x2) qui avait l'autre extrémité B' devant lui quand son horloge indiquait t = ... (événement E2).
On mesure ensuite la distance L = x2 – x1. La transformation de Lorentz-Poincaré, nous donne le résultat qui est le même à tout instant t : soit | 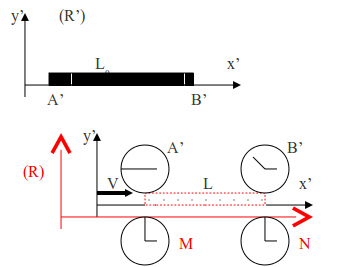 |
La longueur n'est plus une grandeur absolue. Le segment MN est une reconstitution, après la mesure, de la position à l'instant t de la règle A'B', mais la figure instantanée proposée, n'est pas une photographie !
Conclusion générale
La relativité change en profondeur notre perception intuitive de l'espace et du temps qui correspond au schéma classique galiléen et kantien.
La théorie d'Einstein, parue en 1905, applique le principe de relativité au cas particulier, « restreint » des référentiels galiléens en ignorant les effets de la gravitation. En effet, un objet soumis à la force de gravitation accélère et le référentiel associé n'est donc pas galiléen. Dix ans plus tard, Einstein généralisera le principe de relativité au cas des référentiels quelconques, ce qui lui permettra de décrire l'interaction gravitationnelle comme une modification de la géométrie de l'espace-temps. Cette seconde théorie sera appelée théorie de la Relativité Générale.
Vidéos :
Vidéos réalisées par Marc Albrecht, disponibles dans un DVD « Expériences fondamentales : vitesse de la lumière et des ondes électromagnétiques Physique 1 » édité par le SCEREN, CNDP-CRDP, Directeur de collection : Jean-Pierre Lièvre.
Téléchargez les animations proposées dans l'article (format swf lisible avec RealPlayer) : animations-relativite.zip
Animations Flash :
http://spiral.univ-lyon1.fr/rich-media/ipn_rtc/ipn_wmv-0_800x600.htm
Bibliographie :
Documents historiques et épistémologiques :
- Albert EINSTEIN, Œuvres choisies, Vol.2 : « Relativité I. Relativités restreinte et générale », Editions du Seuil, Editions du CNRS, 1989.
- Jean-Claude BOUDENOT, « Comment Einstein a changé le monde », EDP Sciences, 2005.
- Emilio SEGRE, « Les physiciens modernes et leurs découvertes. Des rayons X aux quarks », Fayard 1987.
- Abraham PAIS, « Albert Einstein. La vie et l'œuvre », Dunod, juin 2005.
Ouvrages de vulgarisation :
- Albert EINSTEIN et Léopold INFELD, « L'évolution des idées en physique », Champ Flammarion, 1982.
- Jean-Marie VIGOUREUX, « L'univers en perspective. Relativité restreinte », Ellipses, 2006.
- Banesh HOFFMANN, « La Relativité, histoire d'une grande idée », Belin Pour la Science, 1999.
Ouvrages d'approfondissement :
- Yvan SIMON, « Relativité restreinte », Editions Armand Colin, 1971.
- Jean HLADIK, Michel CHRYSOS, « Introduction à la Relativité restreinte », Edition Dunod, 2001.
- D. Sivoukhine, « Cours de physique générale, tome IV optique », Editions Mir, Moscou
L'ensemble des articles de ce dossier a été présenté lors d'une conférence : pour écouter en ligne la conférence, synchronisée avec les diapositives et le plan de la conférence : « La relativité restreinte » (durée : 1 h 10 min).
Article précédent : « Les principes de la relativité restreinte - Relativité restreinte (2/3) »
Dossier "La relativité"
Pour citer cet article :
Validation des principes de la relativité restreinte - Relativité restreinte (3/3), Marc Vincent, juillet 2012. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/validation-relativite-restreinte-3.xml