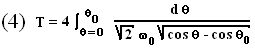Les horloges

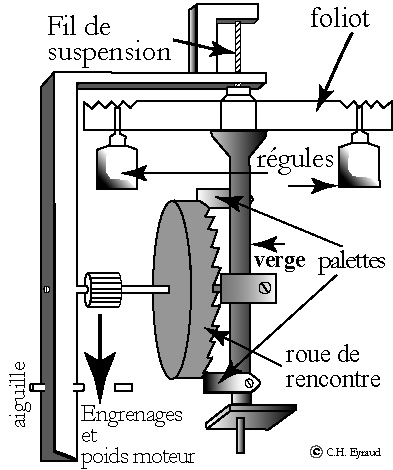
Figure 1. Une horloge à foliot

Inventée vers le XIII^ième ou XIV^ième siècle, cette horloge est constituée d'un balancier oscillant, le foliot, dont l'oscillation est entretenue par une roue qui tourne sous l'effet d'un poids. Le foliot est relié à une verge munie de palettes qui tour à tour stoppent ou permettent le mouvement de la roue de rencontre.

Les horlodes à foliot étaient très imprécises et devaient être remises à l'heure tous les midis à l'aide d'un cadran solaire.

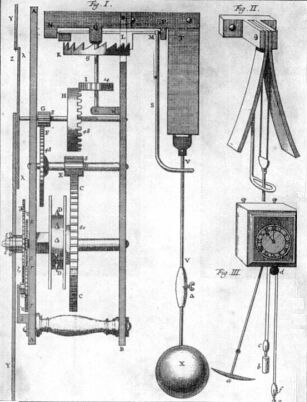
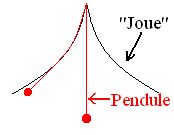
Galilée, le premier, remarque l'intérêt du mouvement régulier du pendule pour la construction d'horloges. Mais c'est Christian Huygens (1629-1695) qui réussira à résoudre les problèmes liés à l'utilisation du pendule (non isochronisme des grandes oscillations) et à inventer une horloge basée sur le pendule pesant, mais dotée d'un système de joues de forme cycloïdale racourcissant la longueur libre du fil à mesure que l'angle du pendule avec la verticale augmente (voir figure). Cette horloge à pendule est bien plus précise que les horloges antérieures.

"Horloguum Oscillatorium", 1673

Figure 2. Le pendule cycloïdal de Huygens (extrait de "Horloguum Oscillatorium", 1673)

D'autres horloges suivront, et l'idée d'utiliser un pendule cycloïdal sera abandonnée par la suite au profit des horloges à ancre plus simples.

Le principe de l'échappement à ancre, inventé en 1660 par William Clément, permet d'obtenir un angle d'oscillation plus faible du balancier, donc une plus grande précision (plus l'angle est faible, meilleur est l'isochronisme des oscillations).

Cathédrale Saint-Jean de Lyon

Guy Bussery

Figure 3. Une horloge à échappement à ancre : l'horloge astronomique de la Cathédrale Saint Jean de Lyon, France

La marine a besoin d'horloges précises pour mesurer les longitudes. Celles-ci peuvent se déterminer en comparant l'heure indiquée par l'horloge à l'heure solaire du lieu. Une erreur de 4 minutes correspond à une erreur d'un degré de longitude. Il est donc impossible d'utiliser une horloge qui peut retarder d'une heure en un jour, ou même de 15 minutes par jour pour les meilleures, comme les premières horloges à foliot! Le problème est essentiel pour éviter des catastrophes dans la marine à tel point qu'un concours est lancé avec un prix pour celui qui construira le premier une horloge permettant de déterminer la longitude en mer avec une erreur inférieure à un degré.

Il y a donc de fortes incitations à cette époque pour améliorer encore la précision des horloges.

George Graham, en 1715, invente l'échappement "à repos sans recul" qui permet de donner une impulsion quasi-instantanée au pendule lorsqu'il passe par sa position d'équilibre.

Le principe de l'échappement à ancre, amélioré au fil du temps, sera très largement utilisé dans les horloges mécaniques.

Utiliser un ressort moteur plutôt qu'un poids permet de miniaturiser le mécanisme et de l'utiliser dans un plan différent du plan vertical. Ainsi, c'est le remplacement du poids par un ressort comprimé (que l'on remonte régulièrement) vers le 14^ième ou 15^ième siècle qui a permis l'apparition des premières "montres".

En fait, on utilisera aussi par la suite un deuxième ressort, le ressort réglant (Huygens, 1675) qui, lui, remplace le balancier traditionnel : ce ressort est aussi appelé "balancier spiral" (voir photo ci-dessous).

On voit ici le balancier spiral et le mécanisme d'échappement à ancre

Figure 4. Vue de près d'un mécanisme d'horloge à ressort

La montre à quartz signe un changement important dans l'histoire de la mesure du temps. Basée sur les propriétés piézoélectriques du quartz, elle supplante très vite la montre mécanique.

Qu'est-ce que la piézoélectricité?

Une lamelle de quartz soumise à une compression mécanique voit apparaître une tension à ses bornes et vice-versa.

A quoi sert le quartz dans les montres à quartz?

Le quartz est l'oscillateur de la montre à quartz, tout comme le foliot, le balancier ou le balancier spiral étaient les oscillateurs des horloges précédentes.

La pile sert à entretenir les oscillations électriques (sa consommation est de l'ordre de 5 μW). Un diviseur de fréquences permet de passer de la fréquence élevée du quartz à la fréquence utile dans les montres. Ce n'est qu'après avoir réussi à miniaturiser les systèmes diviseurs de fréquence, avec l'apparition des transistors puis des circuits intégrés que le principe de l'horloge à quartz, connu depuis 1920, a pu vraiment être mis en pratique sous une forme intéressante.

Enfin, un micromoteur permet de transformer ces oscillations électriques en mouvement des aiguilles (voir schéma).

Gabrielle Bonnet

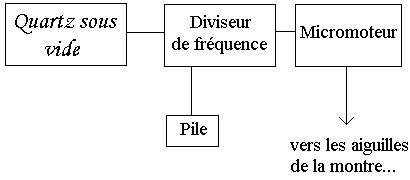
Figure 5. 

Si les horloges à quartz ont envahi notre vie quotidienne, ce ne sont cependant pas elles que l'on utilise aujourd'hui lorsqu'on veut mesurer le temps de façon très précise. L'horloge atomique (la première date de 1954) est la plus précise des horloges et est à la base de notre définition actuelle de la seconde. Ainsi, cette-dernière n'est plus définie à partir de mouvements astronomiques, mais à partir des fréquences de transition atomiques : par définition, la fréquence de transition entre les niveaux hyperfins de l'état fondamental de Césium 133 est 9 192 631 770 Hz.

Dans le cas de l'horloge à foliot, le foliot peut bouger quasi-librement autour de son axe (le couple de rappel du cordon de suspension est très faible). Ce sont les palettes qui, en butant contre la roue de rencontre, limitent son amplitude de rotation.

Ainsi, la vitesse angulaire de rotation θ' du foliot est à peu près constante et la période T est déterminée par le rapport entre l'amplitude maximale permise A et la vitesse angulaire : T = A/θ'.

Le défaut majeur de cette horloge est que le système n'a pas de période propre. Une quelconque perturbation de θ' ou de A se traduit par une variation en conséquence de la période.

Ceci explique l'imprécision de ces horloges, si grande qu'elles devaient être remises à l'heure tous les jours!

Nous allons maintenant étudier les horloges mécaniques et les horloges à quartz en parallèle, en commençant par le principe de l'oscillateur idéal, puis en étudiant les différents écarts entre cette version simplifiée et les horloges réelles, pour arriver enfin à une compréhension minimale de la complexité d'une véritable horloge.

Mécanique	Electrique
Considérons un pendule constitué d'un balancier pouvant osciller librement autour d'un axe horizontal Δ 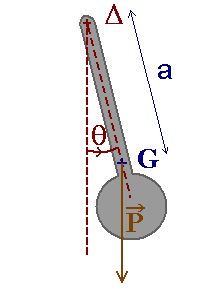Gabrielle Bonnet Figure 6.  Dans le cas de l'oscillateur idéal, il n'y a pas de frottement.	Pour comprendre le principe d'une horloge à quartz, il faut étudier son composant essentiel : une lamelle de quartz placée entre deux électrodes, symbolisée par le schéma : 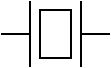Gabrielle Bonnet Figure 7.
Pour éviter d'avoir à introduire le moment d'inertie du balancier, on peut modéliser, au niveau Terminale, le pendule par une masse "ponctuelle" suspendue au bout d'un fil inextensible (pendule simple). Les équations auxquelles on aboutit sont identiques dans leur forme mathématique et ce modèle est suffisant pour comprendre le principe d'une horloge à balancier. 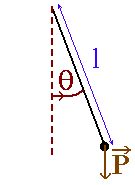Gabrielle Bonnet Figure 8.  Dans le "cas idéal", il n'y a pas de frottement.	On peut modéliser, au niveau Terminale, le quartz placé entre deux électrodes par le schéma équivalent suivant : 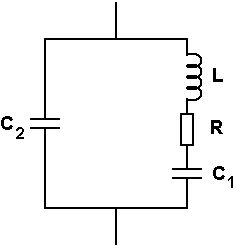Gabrielle Bonnet Figure 9.  le quartz est équivalent à un circuit L, R, C1 série (L, R et C1 ne dépendent que des caractéristiques physiques du quartz) placé en parallèle avec une capacité C2 qui correspond à la capacité créée par les deux électrodes qui enserrent le morceau de quartz.
Si l'on étudie le mouvement du balancier dans le cas du pendule réel, le théorème du moment cinétique donne : dL/dt = M/Δ L : moment cinétique du balancier M : moment des forces par rapport à l'axe Δ avec L = ∑ ri ^ pi = I ω uΔ I ( = ∑ miri2) est le moment d'inertie du solide par rapport à l'axe Δ, ω, sa vitesse angulaire de rotation et uΔ le vecteur unitaire colinéaire à Δ. Le moment des forces par rapport à l'axe Δ, en l'absence de frottements, se ramène au moment du poids du balancier, on a : M = rG ^ P = - a m g sin θ uΔ on obtient alors l'équation : I θ" + m a g sin θ = 0 θ" + ω02 sin θ = 0 ω02 = m g a / I L'étude d'un poids ponctuel suspendu au bout d'un fil de longueur l donnant : θ" + ω02 sin θ = 0 avec ω02 = g / l on obtient une équation qui est mathématiquement identique à celle que l'on obtient dans le cas du mouvement du balancier, justifiant ainsi de se ramener au cas d'une masse ponctuelle suspendue au bout d'un fil pour comprendre le principe des horloges à balancier. Dans le cas idéal, on se limite aux petites oscillations du pendule au voisinage de sa position d'équilibre, soit sin θ ≃ θ ce qui donne θ" + ω02 θ = 0	Dans le cas idéal, on suppose qu'il n'y a pas de perte d'énergie, c'est-à-dire que R ≃ 0 il n'y a donc pas besoin de pile pour entretenir les oscillations. Le circuit "idéal" est alors un simple circuit L, C où la capacité C équivalente à C1 et C2 en série vérifie : 1/C = 1/C1 + 1/C2 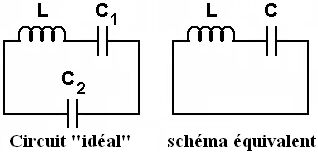Gabrielle Bonnet Figure 10.  L'équation correspondant à cette situation s'écrit : I" + ω02 I = 0 pour l'intensité et U" + ω02 U = 0 pour la tension aux bornes de L, C ou, de façon équivalente, aux bornes de L, C1avec ω02 = (L C)-1/2

Les solutions des équations pour l'horloge à balancier aussi bien que pour l'horloge à quartz sont de la même forme :

pour le pendule mécanique "idéal" et

pour un circuit L, C sans perte énergétique.

La période T = 2 π /ω₀ des oscillations ne dépend pas de leur amplitude mais uniquement des caractéristiques de l'oscillateur (et de g dans le cas du pendule).

On va étudier ces problèmes successivement.

Cas des "grandes" oscillations

Lorsqu'on étudie un pendule mécanique, l'équation différentielle à laquelle obéit le pendule, même en négligeant les frottements, est en fait une équation passablement complexe faisant intervenir une dépendance en sin θ :

(1) θ" + ω02 sin θ = 0

et ce n'est qu'au premier ordre en θ (pour θ ≪ 1) que l'on a l'équation linéaire :

θ" + ω₀² θ = 0

Evidemment, l'équation (1) est plus difficile à résoudre.

On se propose dans ce qui suit de montrer comment on obtient la période de l'oscillation dans le cas non-linéaire.

En termes énergétiques on peut écrire :

(2) θ'2/2 + ω02 (1 - cos θ) = constante

Si θ₀ est l'amplitude maximale des oscillations, ceci donne :

θ'²/2 + ω₀² (1 - cos θ) = ω₀² (1 - cos θ₀)

soit

(3) θ'2/2 = ω02 (cos θ - cos θ0)

Représentation dans l'espace des phases (cette partie est inutile si on veut seulement déterminer la période, mais extrêment importante en physique)

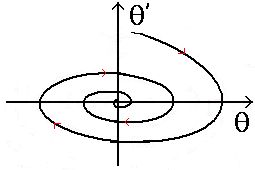
On traduit généralement l'équation (3) par un diagramme dans l'espace des phases (θ, θ') du pendule :

Gabrielle Bonnet

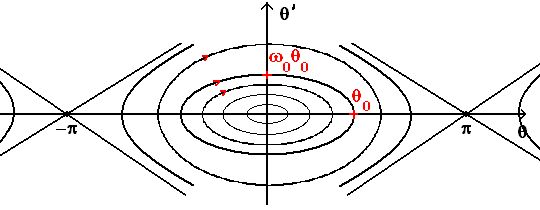
Figure 11. 

• Les courbes θ'²/2 + ω₀² (1 - cos θ) = constante se traduisent, dans le cas des petites oscillations (θ et θ' ≪ 1), par des ellipses centrées sur le point d'équilibre (θ = 0, θ' = 0), que le pendule parcourt dans le sens indiqué par les flèches sur le schéma.

  En effet, l'expression ci-dessus devient θ'²/2 + ω₀² θ²/2 = constante

• Pour θ plus grand, on obtient des ellipses déformées

• (θ = π, θ' = 0) correspond à un équilibre instable.

  Intéressons-nous au comportement du pendule au voisinage de ce point :

  θ = π + ε

  l'équation (2) devient alors :

  ε'²/2 + ω₀² (1- cos(π + ε)) = ε'²/2 + ω₀² (1 + 1 - ε²/2) = ε'²/2 - ω₀² ε²/2 = constante

  • θ₀ = π entraîne ε = 0 quand ε' = 0 donc ε' = ± ω₀ ε : les courbes passant par le point (π , 0) sont des droites au voisinage de ce point
  • Si θ₀ ≠ π, on a l'équation : ε'²/2 - ω₀² ε²/2 = constante ≠ 0 : les courbes au voisinage du point (π , 0) sont des hyperboles

  le point (π , 0) (ou (-π , 0) vu qu'il y a périodicité en θ) est le seul par lequel passent deux courbes différentes. La moindre perturbation dans un sens ou dans un autre de cet équilibre instable peut donner naissance à des comportements ultérieurs très éloignés.

Calcul de la période du pendule

On considère des oscillations d'amplitude maximale θ₀. On peut écrire que la période T du pendule vérifie :

T = ∫_{toute la période}dt = ∫_périodedθ/θ' = 4 ∫_{1/4 de période}dθ/θ' donc

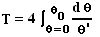
on a (équation (3) précédente, valable quel que soit θ₀) : θ'²/2 = ω₀² (cos θ - cos θ₀) donc

Ce qui nous intéresse, c'est d'estimer l'erreur que l'on fait en supposant que T ne dépend pas de θ₀. Pour cela, il suffit de calculer le développement de T au premier ordre non nul dépendant explicitement de θ₀.

On obtient, après quelques calculs que vous pouvez lire ici, si vous le souhaitez :

(5) T = T0 (1 + θ02/16)

T₀ = 2π/ω₀ est la période propre du mouvement dans l'approximation des petites oscillations.

Interprétation

Alors qu'il y a isochrononisme des petites oscillations, la période dépend de l'amplitude des oscillations dès que celle-ci est assez grande.

Peut-on estimer l'erreur que cela entraîne pour une horloge?

Supposons que, du fait de perturbations extérieures (par exemple le roulis sur un bâteau!), l'amplitude θ₀ des oscillations du balancier varie de dθ₀ au cours du temps. La variation subséquente de la période est :

d T = T₀/8 θ₀ dθ₀ en première approximation.

Application numérique : si T = 1 s et que, suite à des perturbations extérieures, θ₀ varie d'un degré, ainsi dθ₀=1°, pour θ₀ = 20°, la période varie de 7,6 × 10^-4 s par seconde;

On a T=1±7,6.10^-4s. Soit un retard de 66 s par jour ou encore 6,7 heures par an.

La période varie de 1,9 × 10^-4 s par seconde si θ₀ = 5° soit un retard de 16 s par jour et 1,7 heures par an.

Par suite, pour d'assez petites oscillations (5°), une perturbation de l'amplitude du pendule suffit à engendrer un retard (ou une avance) relativement importante de l'horloge.

Une horloge simplement constituée d'un pendule pouvant osciller autour d'un axe horizontal, même dans le cas "idéal" sans frottement (on va se préoccuper du problème des frottements dans le paragraphe suivant), transportée sur un bâteau, par exemple, étant donné les mouvements de roulis et de tangage de ce-dernier, ne serait donc plus assez fiable pour servir au calcul des longitudes.

On verra au paragraphe 3 les solutions apportées à ce problème.

Amortissement des oscillations

Un autre problème majeur est celui de l'amortissement des oscillations, et son corollaire : le problème du choix de la méthode d'entretien des oscillations.

Si on modélise l'amortissement des oscillations par un frottement linéaire en θ', on a l'équation :

m l θ" = - m g sin θ - k θ'

soit

θ" + 2/τ θ' + ω₀² θ = 0

pour l'oscillateur mécanique dans l'approximation des petites oscillations.

Cette équation est la même mathématiquement que celle que l'on obtient pour le schéma équivalent à l'oscillateur à quartz non entretenu :

Gabrielle Bonnet

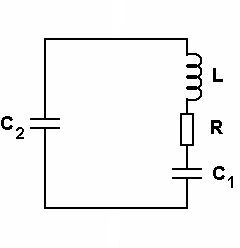
Figure 12. 

L I" + R I' + I/C = 0 (avec C = (1/C₁ + 1/C₂)^-1) soit I" + 2/τ I' + ω₀² I = 0, ω₀² = (LC)^-1 et τ = 2 L/R ne dépendant que des caractéristiques du quartz et des électrodes entre lesquelles il est placé.

La solution d'une telle équation est :

θ = θ₀ e^{- t/τ} sin (ω t + φ)

ou

I = I₀ e^{- t/τ} sin (ω t + φ)

avec ω = (ω₀² - 1/τ²)^1/2 (on suppose l'amortissement suffisamment faible pour que ω₀ > 1/τ)

Le temps séparant deux passages en θ = 0 (ou I = 0) ne dépend pas de l'amplitude des oscillations et est, dans tous les cas, T = 2 π/ω

La durée des oscillations (dans l'approximation des petits angles pour le pendule), reste constante au cours du temps, en dépit de la non-périodicité du mouvement due à l'amortissement des oscillations.

Problème : il faut entretenir ces oscillations pour qu'elles ne cessent pas... le système d'entretien des oscillations va-t'il perturber la période de l'oscillateur? Réponse au paragraphe 3...

dans le cas où le pendule amorti effectue de grandes oscillations (on a donc une équation non linéaire, en sin θ, incluant en outre un terme d'amortissement) l'amortissement des oscillations, de façon prévisible (cf formule (5)) entraîne une diminution de la durée des oscillations au cours du temps. Si on représente le problème dans l'espace des phases (θ , θ'), les trajectoires qui étaient précédemment des ellipses d'autant plus déformées que θ0 était grand deviennent des spirales (déformées pour les grandes valeurs de θ) tendant vers le point d'équilibre (θ = 0 , θ' = 0).

Gabrielle Bonnet

Figure. Une trajectoire possible pour le pendule représenté dans l'espace des phases (θ , θ')

la force de frottement que nous avons introduite dans nos équations est un modèle destiné à nous aider à comprendre la situation réelle. Cependant, cette-dernière peut être passablement plus complexe : le frottement peut avoir une expression différente, plus difficile à traîter mathématiquement, évoluer dans le temps... Autant de problèmes à prendre en compte dans les horloges réelles.

Huygens a cherché à construire un pendule rigoureusement isochrone, quelle que soit l'amplitude des oscillations. La période du pendule, malheureusement, augmente avec l'amplitude maximale θ₀ de ce-dernier (cf équation (5)). Cependant, on sait aussi que T₀ = 2 π (l/g)^1/2 diminue si on diminue la longueur l du pendule. L'idée de Huygens est donc de faire un pendule tel que la longueur de fil diminue lorsque l'amplitude augmente pour "compenser" l'augmentation de la période avec l'amplitude. On peut réaliser un tel pendule en dessinant des "joues", comme sur la figure ci-dessous, sur lesquelles s'enroule le fil du pendule.

Gabrielle Bonnet

Figure 13. L'idée de Huygens : racourcir la longueur de fil du pendule lorsque l'amplitude augmente

Huygens a cherché à trouver la courbe exacte qui permettrait un parfait isochronisme des oscillations, quelle que soit leur amplitude. Alors que Galilée, antérieurement, pensait que le cercle répondait à ces critères, on peut montrer que ce n'est pas la cas. Le problème n'était donc pas encore résolu lorsque Huygens s'y est attaqué. Il a réussi à prouver, au terme d'une longue démonstration (32 pages) que la courbe recherchée est une cycloïde.

Figure 14. Le pendule cycloïdal

La démonstration (enfin, la version analytique que nous proposons et qui fait tout de même moins de 32 pages...) étant assez calculatoire, elle ne convient qu'au lecteur très intéressé... Pour la voir, cliquer ici.

La méthode historique de Huygens, fort différente de la démonstration que nous avons proposée, a consisté à se ramener tout d'abord au problème équivalent consistant à trouver le profil tel qu'une masse glissant sans frottement le long de ce profil mette le même temps à atteindre son point le plus bas, quel que soit le point d'où elle a été lâché. Il a démontré que ce profil est une cycloïde.

Par la suite, par un raisonnement géométrique, il a montré que la joue permettant à la masse du pendule de décrire une cycloïde est elle-même une cycloïde.

Tout oscillateur réel (mécanique ou électrique) est amorti, il est donc nécessaire d'entretenir les oscillations.

Problème :

ce système d'entretien perturbera-t'il la période des oscillations?

On montre que le système idéal d'entretien des oscillations perturbant le moins la période de ces-dernières donne une impulsion quasi-instantanée au voisinage de la position d'équilibre du pendule.

Explication qualitative :

Soit un pendule amorti dans le domaine des "petites oscillations" (domaine linéaire).

Pour mémoire, on rappelle que l'amplitude θ des oscillations est de la forme :

θ = A e^{- t/τ} cos(ω t + φ)

ω et τ ne dépendent que des caractéristiques de l'oscillateur (longueur du pendule, intensité des frottements) et de la valeur de g et sont donc indépendants des conditions initiales.

Si on donne une impulsion "instantanée" au pendule à l'instant t = t₀, on ne change pas θ(t₀) mais, par contre, on augmente θ'(t₀) (on fournit de l'énergie cinétique au pendule).

Si l'impulsion est donnée à θ = 0,

avant impulsion, on a l'équation :

θ_-(t) = A e^-t/τ sin(ω t + φ)

l'impulsion est donnée à t₀ tel que ω t₀ + φ = 2 k π/ω (k entier)

Après impulsion, on a :

θ₊(t) = A' e^-t/τ sin(ω t + φ)

car θ_-(t₀) = θ₊(t₀) = 0 impose φ' = φ

Après impulsion, φ n'a donc pas changé, et seule l'amplitude des oscillations (via la valeur de A) a été modifiée. L'intervalle de temps séparant deux passages à θ = 0 avec une vitesse orientée dans le même sens (c'est-à-dire la période du pendule entretenu) est alors 2π/ω indépendante de la valeur de l'impulsion donnée.

Si, par contre, on donne une impulsion lorsque θ est proche du maximum

(c'est-à-dire lorsque la vitesse du pendule est quasiment nulle donc lorsque θ' ≃ 0) , comme tout à l'heure, on ne modifie pas θ mais on modifie la vitesse θ' qui, après impulsion, n'est plus quasiment nulle.

Cette nouvelle vitesse non nulle du pendule correspond à une phase φ' ≠ φ. Par conséquent, le temps mis par le balancier pour revenir en position haute ne correspond pas à 2π/ω mais à une durée d'oscillation "tronquée" du temps correspondant à la différence de phase φ' - φ.

On peut peut-être comprendre cela de façon plus intuitive en se disant que, si l'on donne une impulsion par exemple exactement au sommet de la trajectoire du pendule (vitesse rigoureusement nulle), après impulsion, le pendule a une vitesse non nulle et ceci ne peut plus correspondre au sommet de sa nouvelle trajectoire. Le sommet de la nouvelle trajectoire après impulsion correspondrait, si on extrapolait cette-dernière avant l'instant t0 où le pendule reçoit l'impulsion d'entretien à une valeur de l'amplitude supérieure, associée à la nouvelle énergie du pendule : la période du pendule est donc tronquée et non plus entière comme dans le cas où l'impulsion a lieu au point le plus bas de sa trajectoire (cf schéma ci-dessous).

Gabrielle Bonnet

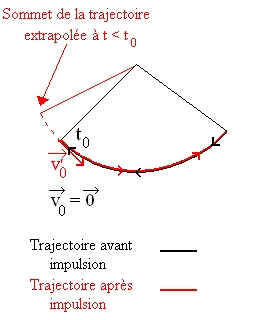
Figure 15. 

Les systèmes réels d'entretien des oscillations fournissent une impulsion la plus constante possible, mais il y a toujours une petite incertitude sur cette impulsion.

Ce que nous venons d'expliquer pour une impulsion à θ = 0 montre que cette incertitude sur l'impulsion n'entraîne aucune incertitude sur la période *. Par contre, au voisinage de θ = θ_max, une incertitude sur l'impulsion donnée se traduit par une forte incertitude sur la période.

Les premières horloges à ancre permettaient de diminuer fortement l'amplitude des oscillations. Ainsi, un meilleur isochronisme des oscillations était-il assuré. Cependant, dans les premiers échappement à ancre, l'impulsion donnée par l'ancre n'était ni instantanée ni donnée au voisinage de la position d'équilibre du pendule.

C'est pour cela que l'invention de l'ancre de Graham, qui utilise un échappement à ancre sans recul (ainsi, la durée de l'impulsion est minimisée), pour lequel l'impulsion est donnée lorsque le pendule est dans sa position d'équilibre, constitue une forte amélioration sur le système d'ancre précédent.

nous avons souligné précédemment l'importance de bien choisir l'endroit où l'impulsion d'entretien des oscillations est donnée de façon à limiter l'influence sur la période des variations de l'impulsion. Bien évidemment, ceci suppose que l'on a tout de même trouvé un système permettant d'avoir une impulsion un minimum constante.

Dans les horloges à poids, c'est en stoppant la chute du poids à intervalles réguliers que l'on empêche ce-dernier d'accélérer et que l'on obtient ainsi une impulsion suffisamment invariante dans le temps.

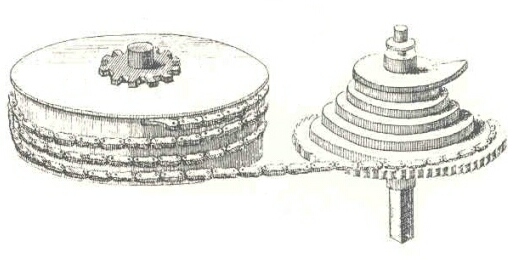
Le problème est plus délicat lorsque l'élément qui remplace le poids est un ressort comprimé. En effet, le couple que ce-dernier exerce sur le balancier diminue avec le temps, au fur et à mesure qu'il se détend. Une innovation technique : la "fusée" a permis de compenser cette variation, en faisant en sorte que le ressort soit lié par une chaîne à une roue de diamètre qui décroît au fur et à mesure qu'il se détend (voir schéma ci-dessous).

Encyclopédie de Diderot et D'Alembert

Figure 16. Image de "fusée" tirée de l'Encyclopédie de Diderot et D'Alembert

Si le profil de la "fusée" est correctement calculé, il permet de compenser la variation du couple moteur et ainsi d'obtenir une impulsion fournie par le ressort suffisamment constante au cours du temps.