Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
La découverte historique de la variation de la pesanteur avec la latitude
10/04/2013
Résumé
Variation de la pesanteur avec la latitude, forme de la Terre, force centrifuge et développement théoriques pour expliquer les observations.
Table des matières
Introduction
Les premières expériences de Galilée, les découvertes de Huygens sur le pendule et les développements théoriques de Newton permettent de quantifier un nouveau paramètre physique pour la Terre : la pesanteur. Dans cet article, nous regardons la découverte puis l'explication des variations de la pesanteur avec la latitude. Nous montrons que l'établissement d'une théorie complète de la pesanteur terrestre a été un processus long et complexe. En particulier, les influences de la force centrifuge due à la rotation de la Terre et de la forme de la planète sur la variation de l'intensité et de la direction de la pesanteur n'ont été comprises que très progressivement. Ce sont ces difficultés pour intégrer l'ensemble des phénomènes dans un système cohérent qui dévoilent les obstacles rencontrés et les avancées graduelles de la pensée. Nous regardons également comment les mesures pendulaires et la forme de la Terre ont permis de départager les deux théories de la gravité de Newton et de Huygens. En annexe, nous proposons une transcription des calculs de Huygens en notation moderne.
Le pendule : instrument de mesure du temps et de la pesanteur
Galilée est l'un des premiers à s'intéresser au mouvement des pendules simples. Il découvre en 1632 que la période du pendule ne dépend ni de sa masse, ni de l'amplitude des oscillations (si celles-ci restent faibles) mais uniquement de sa longueur. Il est donc facile de déplacer un pendule et de reproduire partout les mêmes oscillations. L'un des buts est alors de trouver par essais la longueur du pendule battant la seconde. Le pendule devient un instrument de mesure du temps.
En 1659, Huygens trouve l'expression exacte de la période d'un pendule : T=2π.√(l/g), où g est la pesanteur. La période dépend de la longueur l du pendule mais aussi d'un paramètre terrestre fondamental : g. Pour un pendule battant la seconde (équivalent à une période de 2 s), on a : g = π2l. En 1690, dans son Discours de la cause de la pesanteur, Huygens indique que la longueur du pendule battant la seconde à Paris est de 3 pieds 8,66 lignes soit 0,9941 m. Cette valeur correspond à une pesanteur à Paris de 9,812 m.s-2 (avec nos unités). Le pendule devient l'instrument de mesure de la pesanteur.
Peut-on se servir du pendule pour établir un étalon de longueur ?
Une des difficultés récurrentes de la physique est de trouver des définitions des unités fondamentales : unités de temps, de masse, de longueur, etc. Ces définitions doivent être précises et universelles pour que tout le monde puisse s'en servir pour faire les mêmes calculs et les mêmes mesures. L'unité de temps (la seconde) est bien définie (à l'époque, la seconde est déterminée par l'observation du mouvement des astres dans le Ciel : il s'agissait de la 86.400ème partie du jour solaire moyen). Si l'on pouvait relier l'unité de longueur à celle du temps, l'unité de longueur deviendrait elle aussi précise. D'où l'idée de Picard, en 1670, de définir l'étalon de longueur, qu'il appelle rayon astronomique, comme étant la longueur du pendule battant la seconde de temps moyen.
Cependant, Richer est envoyé à Cayenne en 1672 pour y mesurer la parallaxe de Mars (afin, par application des lois de Kepler, de connaître enfin la distance Terre- Soleil et ainsi toutes les distances dans le système solaire), et il fait une découverte essentielle. Huygens rapporte en 1690 : « L'on assure d'avoir trouvé dans la Cayenne, qui est un pays dans l'Amérique, éloigné seulement de 4 à 5 degrés de l'équateur, qu'un pendule qui bat les secondes, y est plus court qu'à Paris d'une ligne et un quart. D'où s'en suit que, si on prend des pendules d'égale longueur, celui de la Cayenne fait des allées un peu plus lentes que celui de Paris. La vérité du fait étant posée, on ne peut douter que ce ne soit une marque assurée de ce que les corps pesants descendent plus lentement en ce pays là qu'en France. Et comme cette diversité ne saurait être attribuée à la ténuité de l'air, qui est plus grande dans la zone torride (parce qu'elle devrait causer un effet tout contraire) je ne vois pas qu'il puisse y avoir d'autre raison, sinon qu'un même corps pèse moins sous la ligne [l'équateur] que sous des climats qui s'en éloignent » ([1], p. 176).
Si la pesanteur varie en fonction de la latitude, l'étalon de longueur définit par Picard ne peut pas être universel et perd tout son intérêt. L'observation de Richer incite à effectuer d'autres mesures pendulaires pour préciser la loi de la variation de la pesanteur avec la latitude.
Cette découverte a également d’autres applications. En effet, pour connaître précisément la longitude d’un lieu, il faut mesurer très précisément le décalage horaire entre l’heure sur un méridien de référence (Paris par exemple) et l’heure locale (une île perdue au milieu du Pacifique, par exemple), et ce sans radio, ni GPS… Les navires devaient donc avoir des horloges qui ne dérivaient pas, appelées « garde-temps ». Il a donc fallu trouver des horloges plus précises que les classiques « pendules » à balancier dont la période variait au cours du voyage. C'est dans ce but, et sous l'impulsion du gouvernement anglais dès 1707, que John Harrison, en 1759, inventa le premier chronomètre précis à la demi-minute par jour (cf., par exemple, Histoire de carte... à la recherche du temps précis).
Comment expliquer les variations de la pesanteur avec la latitude ?
L'effet de la rotation terrestre
La diminution de la pesanteur avec la latitude est aussitôt interprétée comme un effet de la rotation terrestre. L'observation de Richer est donc, si l'on excepte le mouvement diurne des astres, la première manifestation de la rotation de la Terre. Huygens explique en 1690 : « Je reconnus, aussitôt qu'on nous eut communiqué le nouveau phénomène, que la cause en pouvait être rapportée au mouvement journalier de la Terre qui étant plus grand en chaque pays, selon qu'il approche plus de la ligne équinoxiale [l'équateur], doit produire un effort proportionné à rejeter les corps du centre, et leur ôter par là une certaine partie de leur pesanteur » ([1], p. 176).
Huygens a déterminé l'expression de la force centrifuge dès 1659. Après la mesure de Richer, il montre que la force centrifuge, due à la rotation de la Terre, est maximale à l'équateur, nulle aux pôles et que sa projection sur la verticale varie comme le sinus carré de la colatitude. Grâce à la valeur connue de la pesanteur à Paris, il calcule d'abord que le rapport de la force centrifuge (par unité de masse) à l'équateur sur la gravité est de m = 1/289 = 1/(17)2. Dans ce calcul, Huygens considère que g est constant selon la latitude mais l'erreur qui provient de cette approximation est très faible. En considérant une Terre sphérique, il détermine ensuite ce que serait la gravité sur une Terre immobile, puis ce que vaut la pesanteur à l'équateur. Il peut ainsi déterminer la diminution de la pesanteur entre Paris et l'équateur. Il trouve cependant une valeur trop faible par rapport à l'observation de Richer (cf. la retranscription des calculs dans l'annexe Variation de la pesanteur à la surface d'une Terre sphérique (calcul de Huygens) ). D'où provient l'écart ? La première explication est de remettre en cause la précision des observations : « mais on ne peut pas se fier entièrement à ces premières observations. (…) Il faut espérer qu'avec le temps nous serons informés au juste de ces différentes longueurs, tant sur la ligne qu'en d'autres climats » ([1], p.179). Avant la publication des Principia de Newton en 1687, Huygens ne soupçonne pas d'autres causes.
En 1672, l'influence des forces centrifuges sur l'intensité de la pesanteur a donc été observée pour la première fois. Quelques années plus tard, un nouveau problème est soulevé, concernant cette fois la direction de la pesanteur et la déviation de la chute libre des corps par rapport à une direction de référence. La Terre étant considérée sphérique, cette direction de référence est la perpendiculaire à la surface passant par le centre de la Terre (appelée direction géocentrique). On suppose que la pesanteur est confondue avec cette direction et ainsi qu'elle est dirigée pour tous les points de la surface vers le centre de la planète. Hooke est le premier en 1679, lors d'une correspondance avec Newton, à affirmer qu'un corps en chute libre ne tombe pas directement selon la direction géocentrique mais selon une direction déviée vers le Sud. Il affirme ensuite clairement que la pesanteur, composée de l'attraction et de la force centrifuge, n'agit pas selon la direction géocentrique, qu'elle n'est pas dirigée vers le centre de la Terre mais qu'elle s'écarte vers l'équateur : “The Perpendiculars or Lines of Gravity or Descent do no where, except under the Poles and Equinoctial, respect the Center of the Earth; but other Centers in the Axis of its Rotation” ([2], p.356).
En 1690, Huygens reprend ces considérations avec une parfaite acuité. Il affirme qu'une corde qui soutient un plomb s'écarte de la direction géocentrique parce qu'elle est rejetée par le mouvement de rotation de la Terre. Il précise : « Cette déclinaison est bien contraire à ce qu'on a supposé, de tout temps, comme une vérité très certaine, à savoir que la corde, qui tient un plomb suspendu, tend directement au centre de la Terre. Et cet angle, d'un dixième de degré, est assez considérable, pour faire croire qu'on devrait s'en être aperçu, soit dans les observations Astronomiques, soit dans celles qu'on fait avec le Niveau »([1], p.181). Ces réflexions posent le problème de la signification de la verticale qui est la direction donnée par le fil à plomb. Cette direction sert de référence pour les observations astronomiques. On a supposé jusqu'à présent qu'elle passe par le centre de la Terre, et ainsi que la position des étoiles est définie de façon unique quelque soit le lieu d'observation. Ce n'est plus vrai si la pesanteur ne tend pas vers un seul centre. Toutes les observations des positions d'étoiles doivent ainsi être revues ! Huygens se trompe cependant lorsqu'il affirme que cette déviation de la verticale peut être observée aisément. Car il n'y a pas de terme de comparaison. La direction géocentrique, qui serait la verticale d'une Terre au repos, ne peut être observée par aucun moyen sur une Terre en mouvement et n'a aucune signification physique.
L'aplatissement de la Terre
L'effet de la force centrifuge étant significatif dans la valeur et la direction de la pesanteur, son influence sur la figure de la Terre et des planètes se pose également. En 1666, Jean-Dominique Cassini observe que Jupiter a une figure aplatie (rayons équatorial et polaires sont de l'ordre de 71492 et 66854 km, soit un aplatissement important de 0,06488, pour cette planète gazeuse qui tourne très vite sur elle-même en seulement 10h). En 1671, Picard est, semble-t-il, le premier à avancer que la Terre n'a pas une forme parfaitement sphérique. Vers 1675, Hooke suppose que les planètes sont des ellipsoïdes aplatis. En 1677, Gallet pense mettre en évidence l'aplatissement de Mercure lors de son passage devant le Soleil (ce qui s'avérera faux par la suite pour cette planète tellurique à très longue période de rotation de 58,6 jours). En 1681, Burnet affirme lui-aussi que la Terre est un ellipsoïde aplati. En 1683, Hooke discute les différentes possibilités pour la forme de la Terre, allongée ou aplatie, sans prendre réellement parti faute d'observation déterminante. En 1683, les astronomes J.-D. Cassini et La Hire commencent à prolonger la méridienne de Picard vers le Sud et le Nord pour tester la forme de la Terre. En 1686-1687, Hooke réémet clairement l'idée que les mers ont une forme ellipsoïdale, du fait de la rotation terrestre ([2], p.346) et il propose de prouver l'aplatissement terrestre par des mesures pendulaires et des mesures géodésiques à différentes latitudes.
Dans ses Principia de 1687, Newton affirme lui aussi que la Terre est aplatie aux pôles. Il expose : « Si les planètes n'avaient point le mouvement journalier de rotation autour de leur axe, elles devraient être sphériques à cause de l'égale gravité de leurs parties. Le mouvement de rotation fait que les parties qui s'éloignent de l'axe font effort pour monter vers l'équateur. Et par conséquent, si la matière dont elles sont composées était fluide, son élévation vers l'équateur augmenterait le diamètre de ce cercle, et son abaissement vers les pôles diminuerait l'axe. Aussi les observations astronomiques nous apprennent-elles que dans Jupiter le diamètre qui va d'un pôle à l'autre est plus court qui celui qui va de l'Orient à l'Occident. Par le même raisonnement, on verra que si notre terre n'était pas un peu plus haute à l'équateur qu'aux pôles, les mers s'affaissant vers les pôles, et s'élevant vers l'équateur inonderaient toutes ces régions » ([3], p.34). Newton postule, sans démonstration, que la figure d'équilibre de la Terre fluide en rotation n'est donc pas une sphère mais un ellipsoïde de révolution. Comme à son habitude, il propose un calcul là où ses prédécesseurs se sont contentés d'affirmations qualitatives. Il détermine l'aplatissement α de l'ellipsoïde (α = (a-b)/a, avec a le rayon équatorial et b le rayon polaire) en appliquant sa théorie de l'attraction générale en 1/r2, en supposant que la Terre est homogène et en utilisant la condition suivante (cf. figure ci-dessous) : deux colonnes fluides communiquant au centre de la Terre et rejoignant l'une le pôle et l'autre l'équateur doivent se faire équilibre1. Pour faire ce calcul, il doit déterminer l'attraction au pôle et à l'équateur d'un ellipsoïde de révolution, et c'est la première fois que l'attraction d'un corps non-sphérique est calculée. L'égalité du poids des deux canaux implique que la colonne rejoignant l'équateur, dont la pesanteur est diminuée par la force centrifuge et par l'attraction d'un corps non sphérique, soit plus longue que celle rejoignant le pôle. Il trouve un aplatissement de α = 5/4 m = 1/230.
En 1690, Huygens propose une autre condition d'équilibre pour la Terre. Celle-ci repose sur la direction de la pesanteur (cf. figure ci-dessous). La Terre garde une forme constante si sa surface est, pour chacun de ses points, perpendiculaire à la verticale : « Cela procède du mouvement journalier de la Terre, et c'est une suite nécessaire de la déclinaison susdite du plomb. Parce que la descente des corps pesants étant parallèle à la ligne de cette suspension, il faut que la surface de tout liquide se dispose en sorte, que cette ligne lui soit perpendiculaire, parce qu'autrement il pourrait descendre d'avantage. Partant la surface de la mer est telle, qu'en tout lieu le fil suspendu lui est perpendiculaire » ([1], p.181). En utilisant cette condition d'équilibre, Huygens cherche l'équation de la courbe méridienne représentant la surface terrestre et il montre que cette courbe se confond avec une ellipse, ce que Newton n'a pas démontré. Puis, en réutilisant la condition d'équilibre de Newton (équilibre des deux canaux partant du pôle et de l'équateur) et en supposant que la gravité est constante à l'intérieur de la Terre, Huygens trouve un aplatissement de α = m/2 = 1/578, plus faible que celui de Newton. La différence des résultats met en évidence leurs conceptions différentes de la gravité.
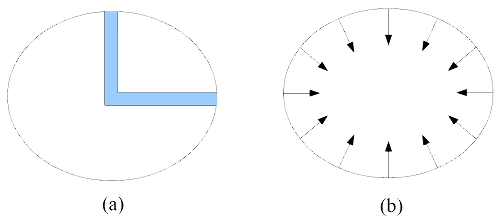
Figure 1. Conditions d'équilibre selon (a) Newton et (b) Huygens
Newton considère que deux canaux partant l'un du pôle et l'autre de l'équateur et se rejoignant au centre de la Terre se font équilibre (a), et Huygens que la surface est en tout point perpendiculaire à la pesanteur (b). Pour calculer la valeur de l'aplatissement, les deux savants utilisent la condition d'équilibre de Newton.
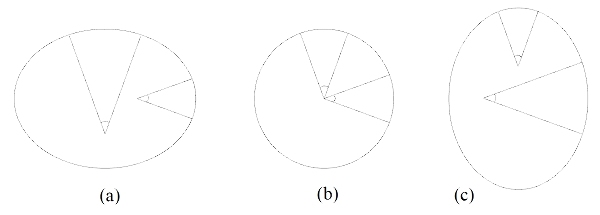
Les verticales qui coupent les méridiens sont des normales à l'ellipse et ne se rencontrent au centre de la Terre que dans le cas de la figure sphérique. L'arc de méridien mesuré près d'un pôle est, selon le modèle, plus long((a) Terre aplatie aux pôles), de même longueur ((b) Terre sphérique), ou plus court ((c) Terre allongée aux pôles), que l'arc de méridien mesuré près de l'équateur.
À la fin du siècle, il existe deux modèles de gravité qui impliquent deux valeurs de l'aplatissement différentes. La figure de la Terre permet donc un premier test entre les deux théories de Newton et de Huygens. La détermination expérimentale de la figure de la Terre n'est cependant pas évidente car il faut pour cela comparer des longueurs d'arcs de méridiens mesurées à des latitudes différentes (cf. figure ci-dessus). Les premières mesures, réalisées en France aux alentours de 1700, semblent donner tort à Newton comme à Huygens puisqu'elles impliquent une Terre allongée selon son axe de rotation ! Pour trancher la question, l'Académie des Sciences de Paris décide, sur ordre du roi, d'envoyer deux expéditions françaises, l'une au "Pérou"* en 1735 (composée de Bouguer, Godin, La Condamine, Jussieu) et l'autre en Laponie en 1736 (composée de Maupertuis, Celsius, Clairaut). La mesure de longueurs d'arcs de méridien à des latitudes très différentes doit permettre de déterminer plus facilement et plus précisément la forme de la Terre. Les mesures réalisées permettent de calculer un aplatissement de 1/178 : les théoriciens l'emportent ! Et puisque cette valeur est beaucoup plus proche de celle donnée par Newton que celle avancée par Huygens, le système newtonien de l'attraction universelle de la matière se trouve renforcé. Cette première preuve de la supériorité de la conception de Newton arrive près de 50 ans après que Newton ait formulé sa loi de la gravitation !
Figure 3. Maupertuis en tenue lapone Gravure avec épigramme par M. de Voltaire : « Le globe mal connu qu'il a su mesurer, / Devient un monument où sa gloire se fonde ; / Son sort est de fixer la figure du monde, / De lui plaire, et de l'éclairer ». In Œuvres de Maupertuis - Nouvelle édition corrigée et augmentée, 1768. | Figure 4. Carte de l'arc méridien de Quito |
Figure 5. Carte de l'arc méridien mesuré au cercle polaire Carte et fin du récit de la mission de Maupertuis au cercle polaire. In Œuvres de Maupertuis - Nouvelle édition corrigée et augmentée, 1768. |
L'expédition de 1735 au "Pérou" permit de mesurer l'arc méridien de Quito, capitale de l'actuel Équateur, alors cité de la vice-royauté du Pérou puis de la vice-royauté de Grenade à partir de 1739.
Pour une formulation moderne des calculs de Newton et de Huygens sur l'aplatissement terrestre, on se reportera à l'article de F. Mignard, 1988. La théorie des figures, in LACOMBE H. et COSTABEL P., La figure de la Terre du XVIIIe siècle à l'ère spatiale. Paris, Gauthier-Villars, p.281-320.
Effet de l'aplatissement de la Terre sur la diminution de la pesanteur avec la latitude
Si la Terre est aplatie, un point de l'équateur n'est pas situé à la même distance du centre de la Terre qu'un point du pôle. Après la lecture des Principia, Huygens reprend donc son calcul de la variation de la pesanteur, en ne considérant plus une Terre sphérique comme il l'a fait la première fois mais une Terre aplatie (cf. figure ci-dessous). Il calcule que la variation de pesanteur provenant de l'aplatissement de la Terre est égale à celle qui provenait de la rotation. En prenant en compte les deux effets (aplatissement et rotation), la variation est donc le double de ce qu'il a trouvé la première fois (Voir l'annexe). La variation calculée est maintenant trop forte par rapport aux observations. Huygens en conclut que seule la rotation agit et il remet en cause la pertinence de la loi de la gravité en 1/r2 dans la proximité des planètes. Il argumente : « Et pour rendre raison pourquoi la seconde variation [la différence d'éloignement] n'aurait pas lieu, je dis qu'il ne serait pas étrange si la pesanteur, près de la surface de la Terre, ne suivait pas précisément, ainsi que dans les régions plus élevées, la diminution que font les différentes distances du centre ; parce qu'il se peut que le mouvement de la matière qui cause la pesanteur, soit aucunement altéré dans la proximité de la Terre, comme il l'est apparemment au dedans » ([1], p.194).
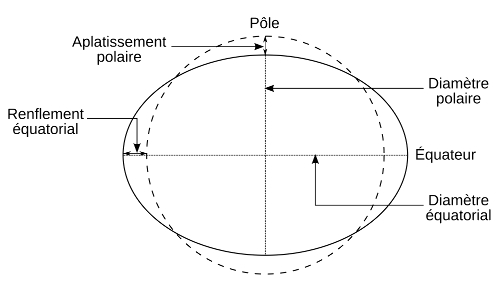
Figure 6. Aplatissement de la Terre en raison de sa rotation journalière
Ellipsoïde aplati aux pôles comparé à une sphère de même volume (cercle en tiretés).
Le rayon terrestre équatorial est de 6378 km et le rayon polaire de 6356 km, soit un aplatissement de 0,00345. La sphère de même volume aurait un rayon de 6367 km (r= (réq x rpol)1/2).
Pour Newton, les choses sont plus complexes. Puisque pour lui, la gravité d'une planète provient de l'attraction gravitationnelle de toutes les particules de matière qui la constituent, elle dépend de la forme de la planète. La gravité à la surface d'une sphère n'est pas équivalente à la gravité à la surface d'un ellipsoïde puisque la répartition de la matière n'est pas identique. Newton invoque trois raisons pour expliquer la diminution de la pesanteur à l'équateur, et seules les deux premières sont acceptées par Huygens : 1) l'effet de la rotation, 2) le plus grand éloignement dû à l'aplatissement de la Terre, et 3) l'attraction d'un corps non sphérique. Un point de l'équateur est certes plus éloigné du centre de la Terre que le pôle mais la diminution de la pesanteur qui en résulte est amoindrie car un point de l'équateur a plus de matière directement sous les pieds que le pôle. Le renflement équatorial compense en partie le plus grand éloignement. Newton ne fait pas une démonstration générale du problème posé, mais il a l'intuition du résultat, qui est juste pour un corps homogène. Il montre que la variation de gravité entre le pôle et l'équateur est égale au quart de la variation provenant de la rotation : la variation de la pesanteur qu'il calcule est trop faible par rapport aux observations ! Il justifie : « Ces différences [dans l'observation de la longueur du pendule dans différentes régions du monde] doivent être attribuées, partie aux erreurs commises dans les observations, partie à la dissemblance des parties internes de la terre, & à la différente hauteur des montagnes, & partie à la différente température de l'air » ([3], p.45). Il envisage donc différentes influences sur les mesures pendulaires, et en particulier l'effet des irrégularités de la surface et de l'hétérogénéité du globe.
Avec les expéditions géodésiques en Laponie et au Pérou, entre 1735 et 1744, de nouvelles mesures pendulaires sont réalisées à différentes latitudes. Celles-ci confirment les résultats précédents (cf. figure ci-après).
Tableau 1. Compilation de mesures pendulaires réalisées lors des expéditions géodésiques en Laponie (1736-1737) [4] et au Pérou (1735-1744) [5]
Lieux | Latitude | Longueur du pendule l (en pouce et ligne) | Longueur du pendule l (en ligne) | Δg/g | g (m.s-2) |
|---|---|---|---|---|---|
Équateur | 0° | 36 pou 7,21 lig | 439,21 | 0 | 9,779 |
Portobello | 9°34' | 36 pou 7,30 lig | 439,3 | 1/4880 | 9,781 |
Petit Goave | 18°27' | 36 pou 7,47 lig | 439,47 | 1/1689,3 | 9,785 |
Paris (Bouguer) | 48°50' | 36 pou 8,67 lig | 440,67 | 1/300,8 | 9,812 |
Paris (de Mairan) | 48°50' | 36 pou 8,57 lig | 440,57 | 1/322,9 | 9,810 |
Pello | 66°48' | 36 pou 9,17 lig | 441,17 | 1/224,1 | 9,823 |
Les longueurs l sont les longueurs d'un pendule de période 2 s. Les variations relatives de pesanteur sont calculées par Δg/g = Δl/l: en prenant comme référence la longueur du pendule à l'équateur. La pesanteur g est calculée avec nos unités en utilisant g = π2l et avec les conversions de longueur suivantes : 1 pouce = 12 lignes et 1 ligne = 0,002256 m.
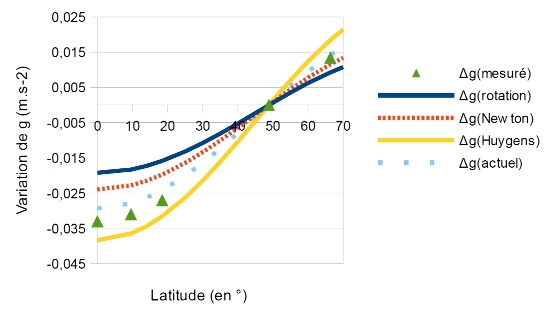
Figure 7. Variation de la pesanteur par rapport à celle de Paris en fonction de la latitude
Pour calculer les variations de pesanteur entre Paris et l'équateur, nous avons utilisé les formules données en annexe. Les triangles verts correspondent aux mesures de Laponie et du Pérou.
La prise en compte de l'hétérogénéité du globe par Clairaut
Les deux conceptions de la gravité de Newton et de Huygens impliquent donc des variations de la pesanteur selon la latitude différentes, ce qui peut donner un nouveau test pour les départager. Malheureusement, aucun des deux modèles ne s'accorde avec les observations : Newton calcule une variation de pesanteur trop faible et Huygens une variation trop forte. Les observations pendulaires ne peuvent donc pas a priori conforter une conception au détriment de l'autre. Cependant le modèle de Huygens ne comporte aucune variable d'ajustement : les observations ne concordent pas et ce résultat est définitif, sans possibilité d'explication future. Au contraire, la non concordance avec les observations ouvre de nouvelles possibilités pour le modèle de Newton. En 1743, Clairaut applique la toute récente méthode de calcul différentiel et intégral au problème de la figure de la Terre. En supposant la loi de la gravitation universelle et en considérant non plus une Terre homogène mais une Terre hétérogène avec une densité qui va en augmentant vers le centre, il montre que les mesures de pesanteur peuvent être parfaitement interprétées. La diminution de la pesanteur du pôle vers l'équateur conforte donc non seulement le modèle de Newton mais en plus elle fournit une des premières contraintes sur la constitution physique de la planète et prouve que la densité augmente avec la profondeur.
Parmi d'autres calculs tous aussi remarquables, Clairaut détermine une relation fondamentale entre l'aplatissement de l'ellipsoïde et les valeurs de la pesanteur au pôle et à l'équateur [6]. Avec nos notations : (gp−ge)/ge=2αh−α, avec gp la pesanteur au pôle, ge la pesanteur à l'équateur, α l'aplatissement de la surface externe et αh l'aplatissement dans le cas homogène (αh=1/230). Cette relation est valable pour tous corps en équilibre hydrostatique. Elle donne un nouveau but aux mesures de pesanteur à différentes latitudes : déterminer la valeur de l'aplatissement terrestre pour pouvoir ensuite la comparer à celle trouvée par les mesures géodésiques. Le grand embarras de Clairaut est que les deux valeurs ne correspondent pas, suggérant que la Terre n'est pas à l'équilibre hydrostatique, ce qui remet en cause la pertinence de sa théorie. Ce n'est qu'au début du XIXème siècle, à la suite de la révision de plusieurs arcs géodésiques, qu'on comprend que le désaccord entre l'aplatissement trouvé par les mesures géodésiques et celui déterminé par les mesures de pesanteur provenait en fait d'une erreur dans la mesure géodésique en Laponie, à laquelle Clairaut avait lui-même participé ! Les deux méthodes donnent enfin des valeurs concordantes, prouvant que la Terre a bien la même figure que celle que prend une masse fluide.
Aujourd'hui, on peut signaler deux avancées majeures du problème.
- La Terre a bien la même figure que celle que prend une masse fluide en rotation. Mais si on s'écarte de cette forme, le retour à l'équilibre prend quelques dizaines de milliers d'années (cf. fonte de la calotte glaciaire scandinave). La viscosité du "fluide" Terre est donc extrême, bien plus visqueux que la glace ou la plupart des métaux dans les conditions ambiantes.
- Des écarts hectométriques existent entre la forme réelle de la Terre (le géoïde) et la forme d'une masse fluide en rotation. Ces (faibles) écarts sont dus, entre autres, à une répartition non exactement concentrique des masses et densités en profondeur.
Conclusion
La gravimétrie est née de l'invention d'un nouvel instrument de mesure (le pendule) qui permit de quantifier une première « constante » universelle physique de la Terre : la pesanteur. De Galilée à Clairaut, en un peu plus d'un siècle d'investigations, la découverte fut que cette « constante » ne l'était pas mais qu'elle variait suivant les latitudes et les lieux ! Les mesures pendulaires eurent pour but initial de mettre en évidence la force centrifuge et ainsi de distinguer la valeur attractive de la masse de la Terre et la valeur répulsive de la rotation. Une fois la force centrifuge reconnue et identifiée, les mesures pendulaires s'intéressèrent directement aux variations de la gravité suivant les lieux. Leur but devint de donner des informations sur la forme de la Terre et, par ce biais, de tester et de départager le système de Newton et celui de Huygens. Avec Clairaut, les mesures pendulaires donnèrent directement accès à la valeur de l'aplatissement, et purent ainsi être confrontées aux mesures géodésiques. Elles posèrent ainsi la question de l'équilibre hydrostatique de la Terre. Elles purent également être reliées à différentes hypothèses sur la constitution de la Terre, montrant ainsi la fécondité du système newtonien pour appréhender les profondeurs du globe.
Bibliographie
CH. Huygens, 1690. Discours de la cause de la pesanteur. Réédition inTraité de la lumière, Paris, Dunod, 1992
R. Hooke, 1687. A Discourse of Earthquakes. Réédition inThe Posthumous Works of Robert Hooke, The source of Science, 73, New York et Londres, Johnson reprint corporation, 1969
I. Newton, 1756. Principes Mathématiques de la Philosophie Naturelle, traduction de la Marquise du Chastelet augmentée des Commentaires de Clairaut. Réédition, Paris, A. Blanchard, 1966
Maupertuis, 1738. La Figure de la Terre, déterminée par les observations…, Paris, Imprimerie Royale, p.180
P. Bouguer, 1749. La Figure de la Terre, Paris, Charles-Antoine Jombert, p.342.
A.C. Clairaut, 1743. Théorie de la figure de la Terre, tirée des principes de l'hydrostatique. Seconde édition, Paris, Courcier, 1808, p.249
C. Larroque, J. Virieux, 2001. Physique de la Terre solide. Observations et Théories, Paris, Contemporary Publishing International, p.20-21.
A. Les calculs de Huygens et de Newton en formulation moderne
Variation de la pesanteur à la surface d'une Terre sphérique (calcul de Huygens)
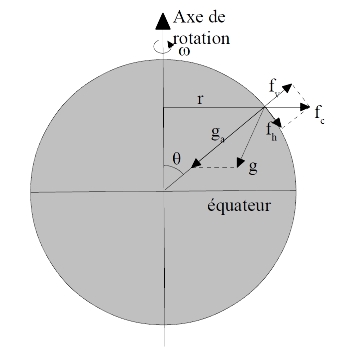
Avec ω la vitesse angulaire de la Terre, RT le rayon de la Terre et θ la colatitude du lieu (cf. figure ci-dessous), la force centrifuge par unité de masse, perpendiculaire à l'axe de rotation, est égale à :
- .
La composante verticale, , a une influence sur la valeur de la pesanteur.
La composante horizontale, , a une influence sur la direction de la pesanteur.
Figure A.1. Pesanteur, gravité de la Terre et force centrifuge
La pesanteur g est la somme vectorielle de la gravité ga de la Terre et de la force centrifuge fc : .
Les valeurs numériques suivantes sont celles de l'époque, mais exprimées avec les unités actuelles :
- vitesse angulaire de la Terre : ω=7,29×10−5 rad.s−1
- rayon de la Terre (détermination de Picard) : RT=6372 km ;
- pesanteur à Paris : gParis=9,812 m.s−2, avec un pendule de période 2s et de longueur l = 3 pieds et 8,66 lignes = 440,66 lignes = 0,9941 m ;
- colatitude de Paris : θ=41,17°.
Le rapport de la composante verticale de la force centrifuge, fv, sur la gravité, ga, est :
- à l'équateur, (dans ce calcul ga est pris égal à gParis) ;
- à Paris, .
La pesanteur d'un lieu de colatitude θ est : .
À paris, on a alors : . Ceci permet de calculer ga, qui est la pesanteur sur une Terre immobile : (ga est également la pesanteur au pôle d'un eTerre sphérique en rotation).
À l'équateur, on a : .
La variation de pesanteur entre Paris et l'équateur est donc égale à 9,812−9,793 = 0,019 m.s−2 , ce qui correspond à une différence dans la longueur du pendule de 1,925 mm, soit 0,853 ligne, valeur qu'il faut comparer à celle trouvée par Richer, à savoir 1,25 ligne.
Aujourd'hui, l'habitude est d'exprimer la pesanteur g d'un lieu quelconque en fonction de la pesanteur ge à l'équateur. Et, puisque cette pesanteur est calculée en tenant compte de la rotation, nous la nommons grotation. On obtient : , et donc .
Les observations actuelles donnent pour le pôle gp = 9,8324 m.s-2 , pour l'équateur ge = 9,7803 m.s-2 et donc Δgobservée=0,0521 m.s−2. La rotation explique 65% de la variation de pesanteur observée.
La variation de la pesanteur à la surface d'une Terre aplatie
Modèle de Huygens
Si la Terre a la forme d'un ellipsoïde de révolution, l'équation de sa surface méridienne est : , avec a le rayon à l'équateur et α l'aplatissement.
La variation de gravité entre un lieu de colatitude θ et l'équateur causée uniquement par l'aplatissement de la Terre (on ne tient pas compte de la rotation) s'écrit :
- , car .
Pour Huygens, l'aplatissement est égal à α=m/2, on obtient donc : . La variation de gravité due à l'aplatissement est égale à la variation de gravité due à la rotation. Lorsqu'on ajoute les deux effets (rotation et aplatissement), on obtient : .
La variation de pesanteur entre le pôle et l'équateur est donc : . Le modèle de Huygens expliquent 130% de la variation de la gravité observée actuellement.
Modèle de Newton
Newton montre que la variation de gravité entre le pôle et l'équateur d'un ellipsoïde homogène est égale au quart de la variation provenant de la rotation. Selon le modèle de Newton, la pesanteur en un lieu de colatitude θ s'exprime par : .
La variation relative de pesanteur entre le pôle et l'équateur est : . Le modèle de Newton expliquent 81% de la variation observée.
Modèle actuel
Les observations actuelles de pesanteur, effectuées à la surface du globe dans un réseau de points de mesure appelée IGSN (International Gravity Standardization Net), permettent de déterminer le champ de pesanteur sur une surface de référence du géoïde (cette surface GRS –Geoid Reference Surface– a reçu une définition stabilisée dans les années 1980, d'où son appellation GRS 80).
Le champ de pesanteur de référence est le suivant [7] :
- g=9,7803185 x [1 + 0,005302357.cos2θ − 0,000005865.cos2(2θ)].
Pour citer cet article :
La découverte historique de la variation de la pesanteur avec la latitude, Vincent Deparis, avril 2013. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/pendule-pesanteur-latitude.xml