Activer le mode zen
Ressource au format PDF
Classification
Onde sonore sur film de savon
16/09/2019
Travail réalisé dans le cadre des XXVIe Olympiades de Physique sous la tutelle de Nora Alleg et Denis Mathiotte, professeurs de Physique-Chimie.
Résumé
Écouter de la musique nous semble naturel mais voir de la musique est beaucoup moins évident. Un simple film de savon nous permet de visualiser les sons. En effet, des figures spectaculaires se forment sur une bulle de savon lorsqu’elle est soumise à une onde sonore.
À partir de différents articles et de thèses, nous avons réalisé un dispositif composé d’un haut-parleur et d’un tube au bout duquel est déposé un film de savon. Pour certaines fréquences, il se forme de magnifiques structures dynamiques comme des vortex avec des irisations. Ces phénomènes sont expliqués par la résonance du tube choisi mais aussi grâce aux interférences lumineuses.
Table des matières
1. Introduction
Baudelaire, dans son poème « Correspondances » tiré des Fleurs du Mal écrivait “Les couleurs et les sons se répondent”. Or, bien que ces synesthésies puissent paraître de prime abord absurdes ou poétiques, elles sont pourtant véridiques. C’est ce que nous allons tâcher de démontrer grâce à un film savonneux qui réagit à la musique. Tout cela est uniquement dû à des phénomènes physiques comme la propagation acoustique, les interférences lumineuses et les propriétés statiques et dynamiques d'un film de savon, qui ne sont, en aucun cas aléatoires.
Nous allons donc tenter de révéler comment une onde sonore invisible à l’oeil nu peut se matérialiser quand elle vient frapper un film savonneux.
Tout d’abord, nous allons observer comment les couleurs apparaissent et comment des vortex se forment sur le film savonneux. Ensuite, nous étudierons les qualités physiques des ondes de surface, en réalisant les calculs nécessaires. Finalement, en guise d'illustration, nous utiliserons notre dispositif pour accorder un instrument, non plus à l’oreille, mais à l’oeil grâce aux ondes capillaires.
2. La musique tout en couleur
2.1 Qu'est-ce qu'une onde sonore ?
Une onde sonore est une onde mécanique progressive. Une onde mécanique progressive est la propagation d’une perturbation de proche en proche avec transport d’énergie mais sans transport de matière. Elle a besoin nécessairement d’un milieu matériel pour se propager.
Les ondes sonores se propagent dans toutes les directions de l’espace, on parle ainsi d’ondes à trois dimensions.
Dans les conditions normales de température (20°C) et de pression (1 atm) la vitesse du son dans l’air est d’environ 340 m.s-1.
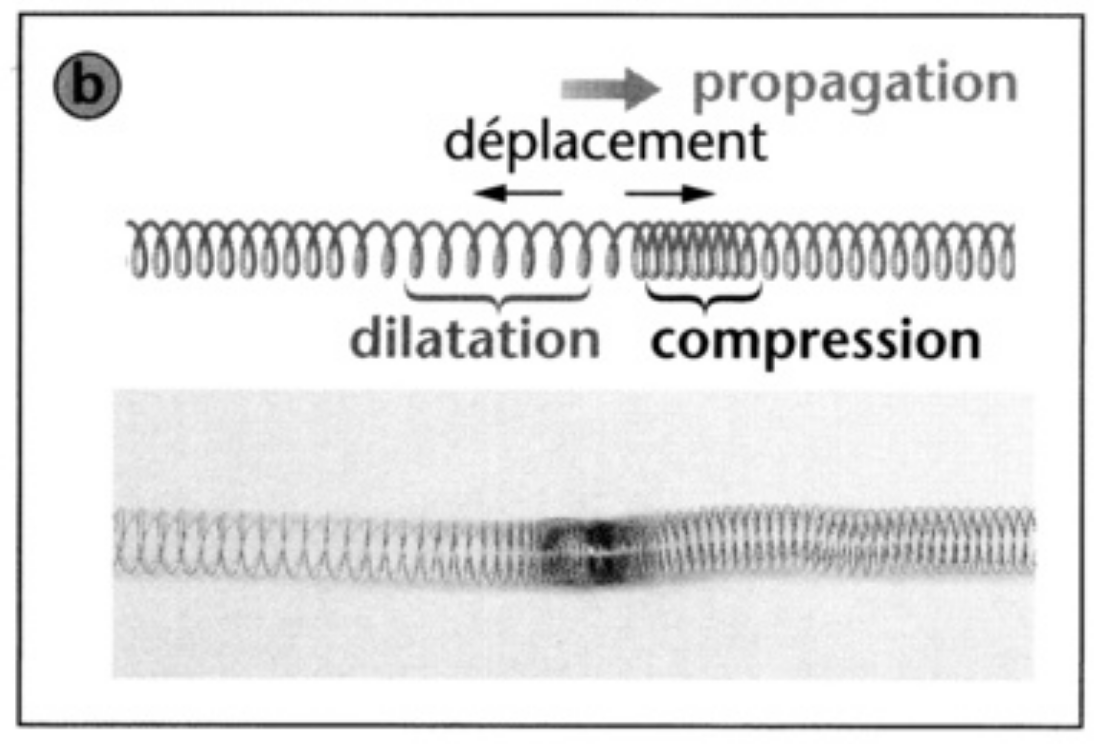
L’onde sonore est caractérisée par une onde longitudinale, figure 1. En effet, la direction du mouvement des éléments du milieu (air…) est parallèle à la direction de propagation de l’onde.
Figure 1. Schématisation de la formation d’une onde longitudinale le long d’un ressort
Source : manuel de Terminale S, Nathan.
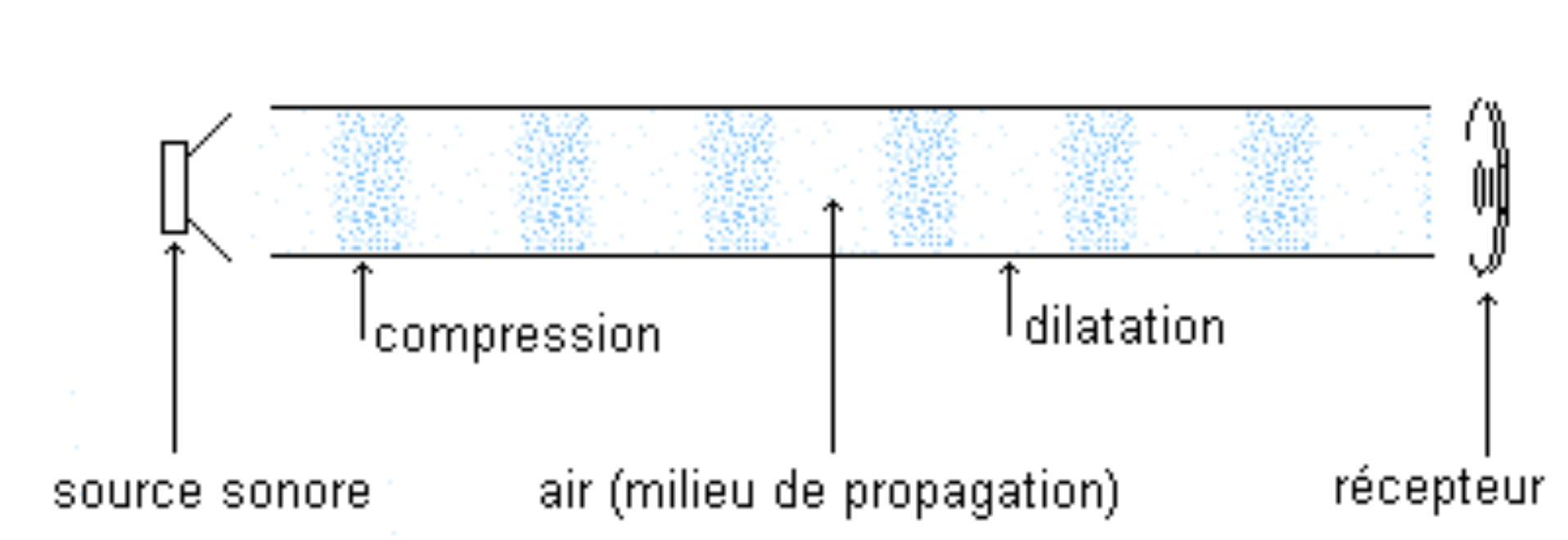
Les ondes sonores se propagent par suite de compressions et de dilatations du milieu de propagation (air…), figure 2.
2.2 Qu'est-ce qu'un son musical ?
En physique, on dit que l’oreille humaine distingue soit le son (caractérisé par une courbe périodique), soit le bruit (matérialisé par une courbe non périodique), figure 3. Ainsi, un son musical est une sensation auditive due aux vibrations du milieu de propagation de l’onde acoustique par une suite de compressions et de dilatations.
Figure 3. Caractérisation d'un son et d'un bruit
Source : http://slideplayer.fr/slide/521107/
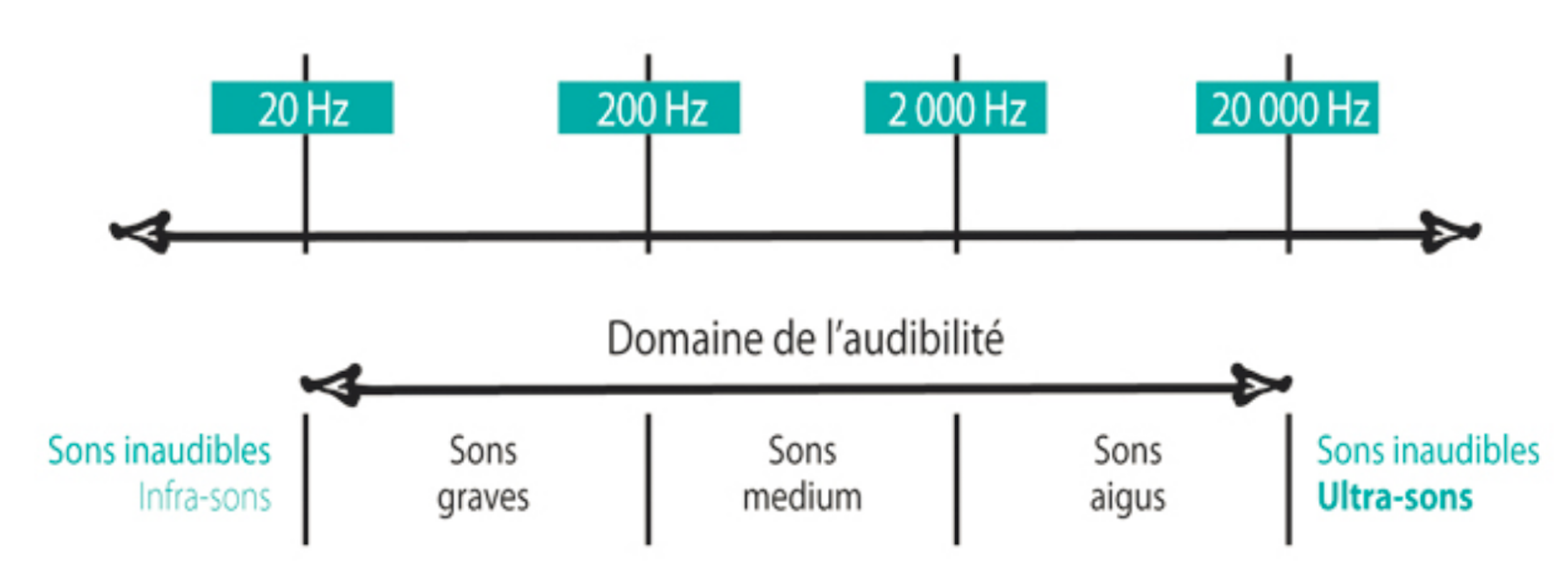
Le domaine de fréquences des ondes sonores perceptibles par l’être humain est compris entre 20 et 20 000 Hertz. Les sons de petites fréquences sont graves, ceux de fréquences élevées sont aigüs, figure 4.
Figure 4. Échelle des fréquences
Un son est caractérisé par sa hauteur, c’est-à-dire la fréquence de l’onde sonore et donc de son fondamental.
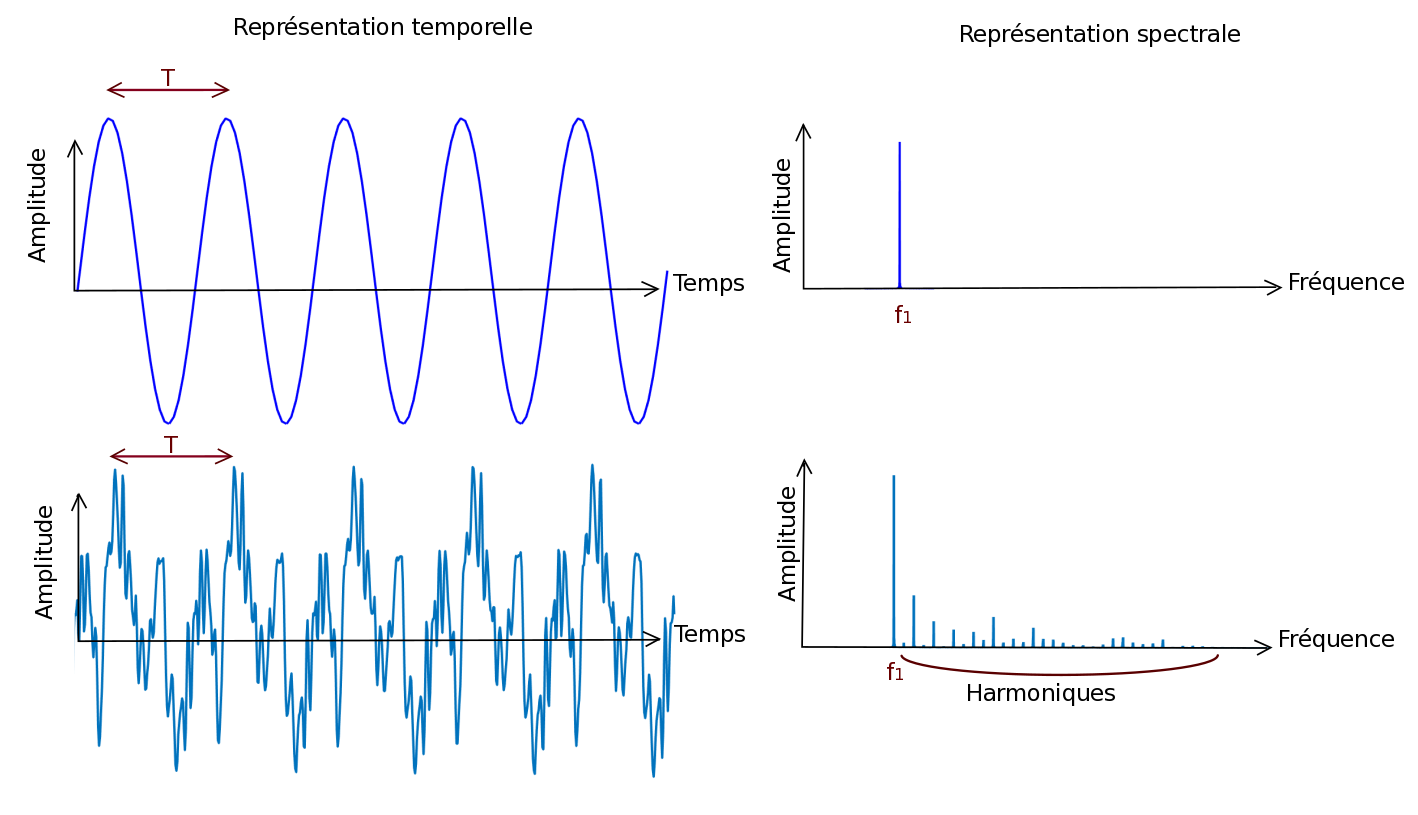
Le son est dit pur quand il a une courbe représentative qui est sinusoïdale, c’est à dire qu’il n’a pas d’harmoniques mais seulement un fondamental. À l’inverse, la voix et les instruments de musique, produisent des ondes également périodiques mais non sinusoïdales. Le son est alors dit complexe, il correspond à la superposition de plusieurs ondes sinusoïdales, figure 5.
Le spectre fait apparaître les fréquences des harmoniques avec leur amplitude relative ce qui constitue le timbre d'un son.
2.3 Comment peut-on voir la musique ?
2.3.1 Montage expérimental
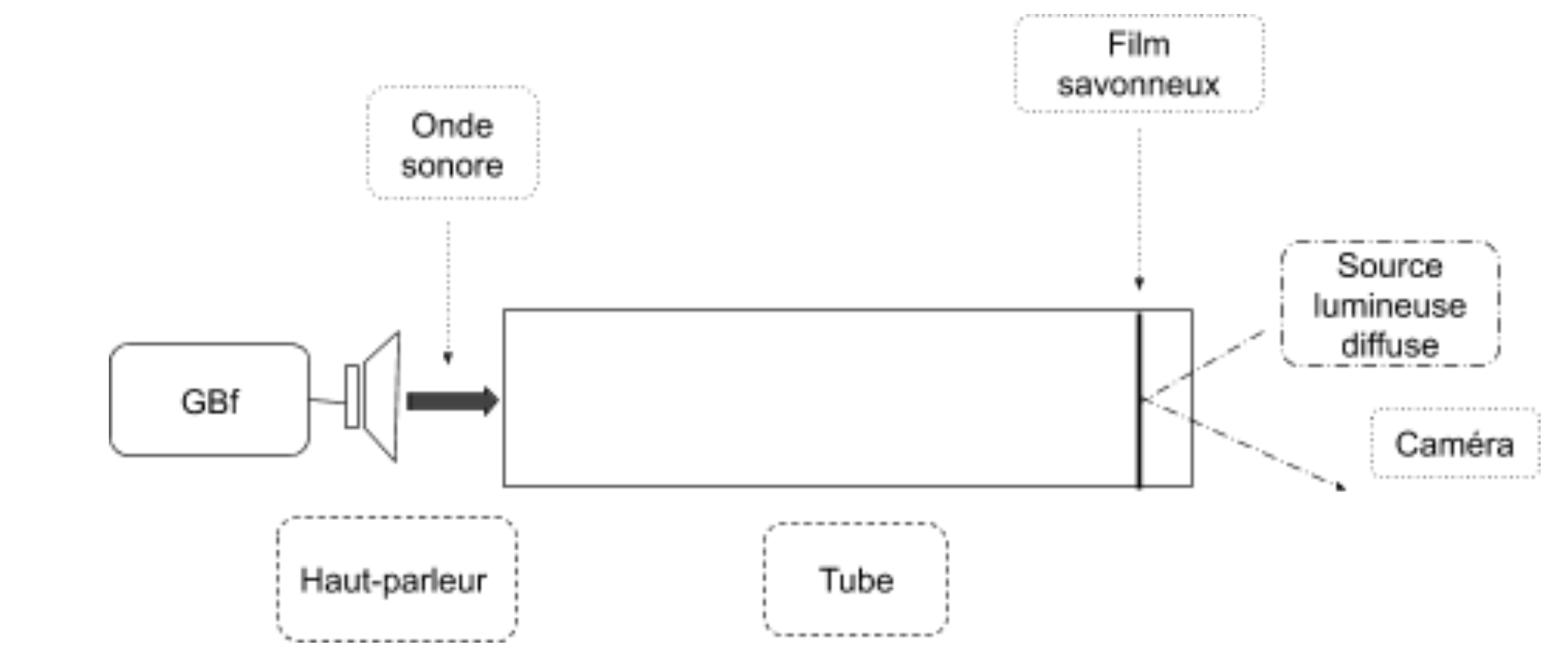
Notre expérience consiste à « voir la musique », c’est-à-dire à distinguer un changement de disposition des figures colorées sur le film savonneux en réaction aux différentes ondes sonores créées par le GBF à la sortie d’un tuyau sonore, figure 6.
Figure 6. Schéma du dispositif expérimental
Le montage expérimental est composé d’un GBF alimentant un haut-parleur. On impose une tension sinusoïdale dont l’amplitude et la fréquence sont réglables ce qui permet de moduler les caractéristiques du son. On dispose, au bout d’un tube en PVC opaque d’une longueur de 1,05 m et d’un diamètre de 50 mm, un film savonneux, figure 7. La longueur que nous avons choisie pour le tube nous permet de travailler avec des fréquences audibles sans être trop désagréables à entendre. L’extrémité du tuyau sera fermée par un film savonneux permettant l’apparition de couleurs interférentielles. Le film savonneux doit être à la fois assez solide pour pouvoir tenir au moins 5 minutes sans éclater et assez fin pour pouvoir distinguer les différentes nuances de couleurs.
Figure 7. Montage expérimental
2.3.2 Formation de la bulle
Après plusieurs tentatives, nous avons finalement trouvé la recette adéquate, à laisser reposer 3 à 4 heures avant l’utilisation, composée de :
- 10 mL d’eau distillée : représentant le solvant ;
- 10 g de sucre ;
- 20 mL de liquide vaisselle professionnel (GEM) : le tensioactif ;
- 60 mL de glycérine.
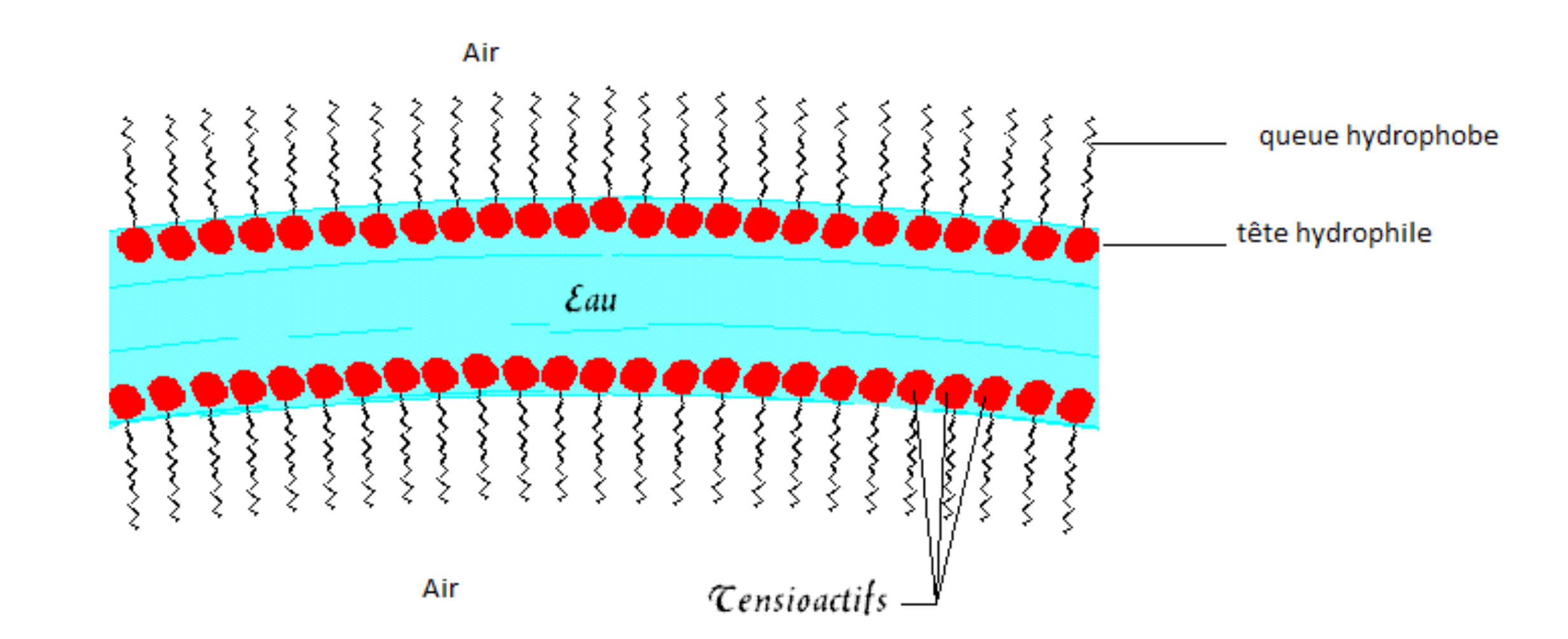
Un savon est constitué d’espèces chimiques ayant un double comportement hydrophile et hydrophobe, figure 8. On parle d’espèces amphiphiles. Les molécules de savon sont de la forme R-COO-Na sous leur forme solide, où R désigne une chaîne carbonée linéaire comportant habituellement un grand nombre d’atomes de carbone (queue hydrophobe) et une partie polaire COO-Na (tête hydrophile).
La présence d’un tensioactif permet de baisser la tension superficielle de l’eau, ce qui permet au film d’étendre sa surface. Cela explique la formation de bulles avec de l’eau savonneuse. La paroi de la bulle est constituée d’une double couche de tensioactifs, emprisonnant un mince filet d’eau. Les liaisons basses-énergies intermoléculaires (hydrogène et Van der Waals) assurent à la structure une certaine cohésion, au moins pendant un temps.
Dans la recette, la présence de glycérine et de sucre permet d’optimiser la stabilité du film grâce aux multiples interactions électrostatiques et à une viscosité plus importante.
2.3.3 Les caractéristiques du film de savon
- La tension superficielle
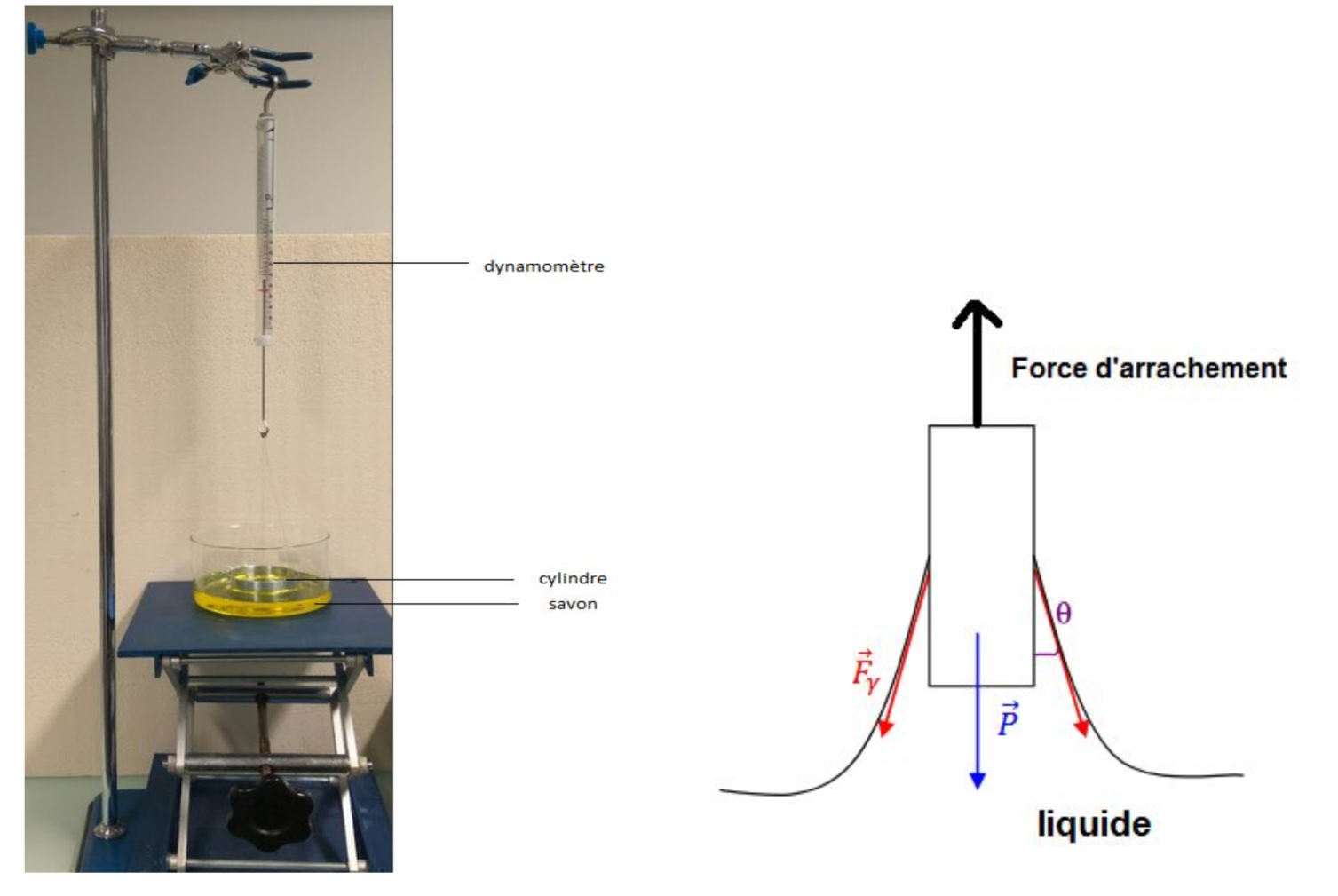
Nous avons mesuré la tension superficielle de notre liquide avec une balance d’arrachement, figure 9.
On cherche la valeur de la force d’arrachement F d’un anneau initialement immergé dans le liquide. Cet anneau est, dans l’air, soumis à son poids P. La valeur de la tension de surface est alors donnée par la formule :
Le rayon de l’anneau est r = 30 mm, les forces F et P sont mesurées plusieurs fois de suite. Suite à ces différents essais, nous avons déterminé une tension superficielle de = (35 ± 4) mN/m
- Explication physique de l'apparition des couleurs sur le film de savon
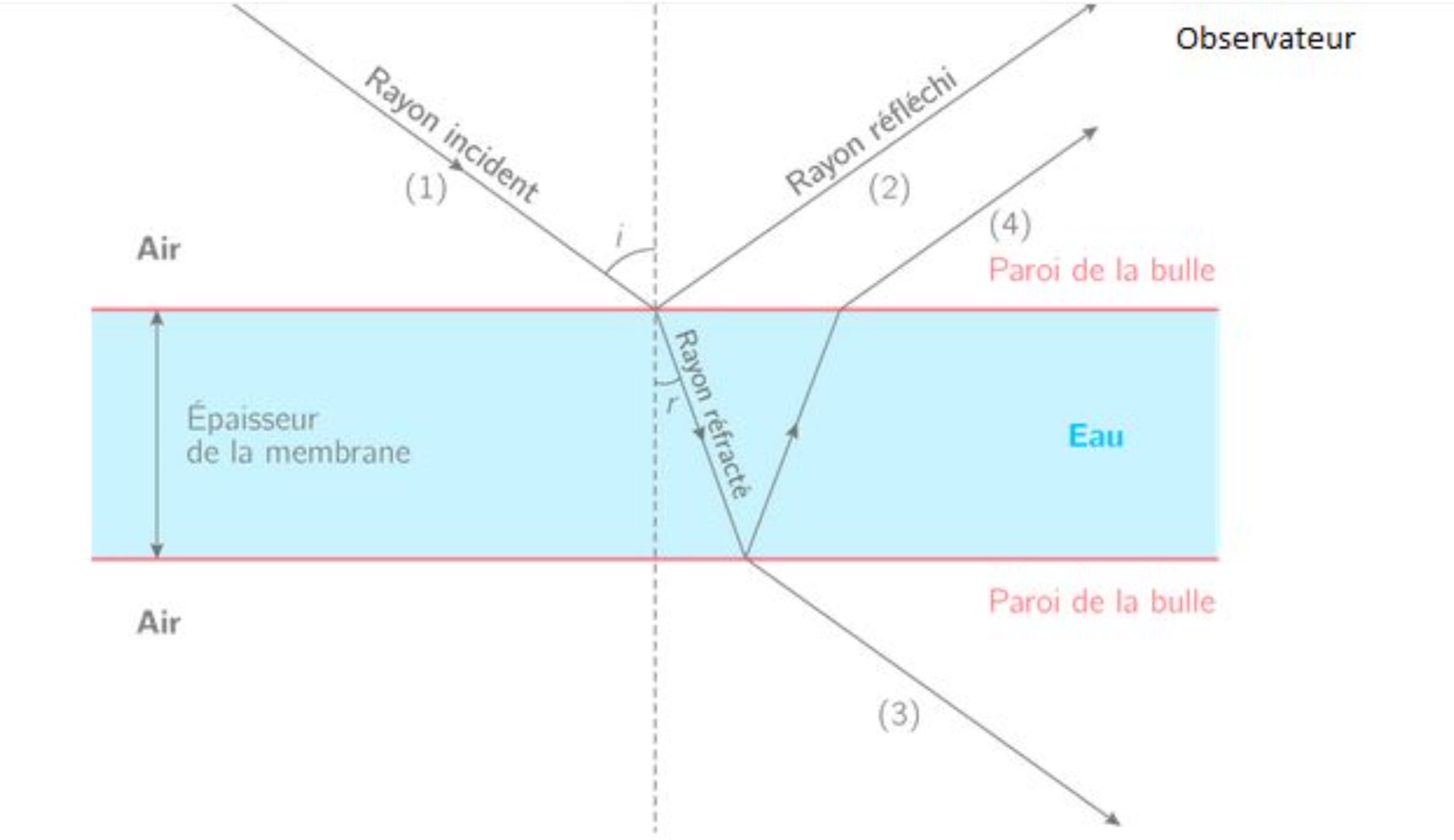
Une partie de la lumière incidente sur la bulle est réfractée dans l’épaisseur e du film et une autre partie est réfléchie à sa surface, figure 10. Les deux rayons sortants (2 et 4), vont entraîner une irisation car ils n’ont pas parcouru la même distance (notion de différence de marche δ).
Cette différence de marche δ correspond à un aller-retour dans l’épaisseur e de la membrane (le rayon 4 a parcouru une plus grande distance que le rayon 2).
Ainsi, δ = d4 − d2 = 2ne, avec n l’indice de réfraction du milieu.
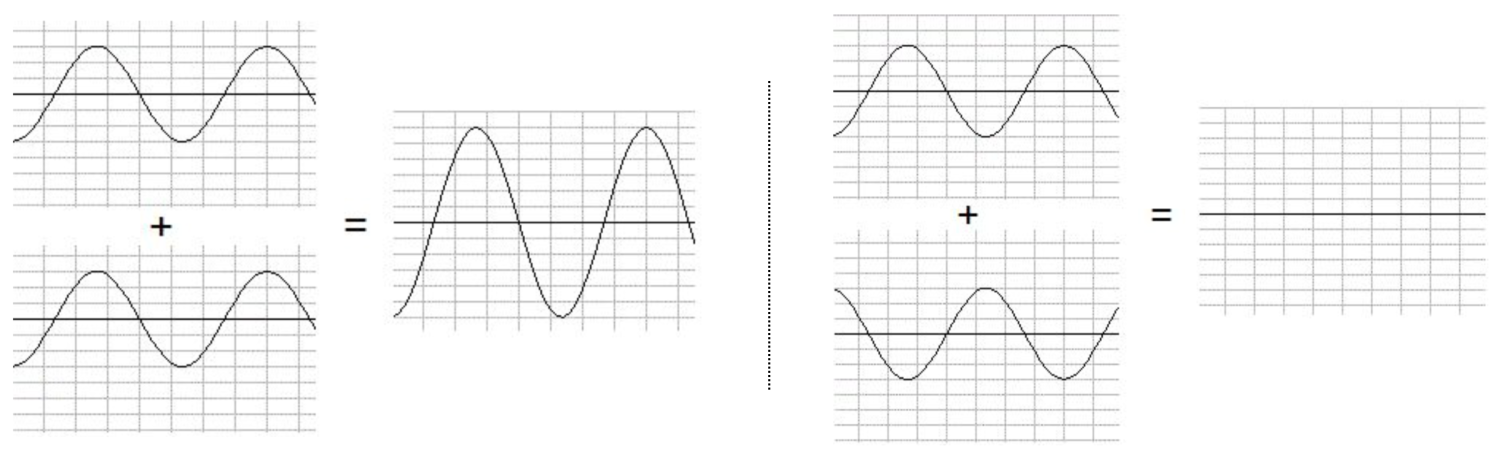
Deux ondes (rayons 2 et 4) provenant d’une même source et ayant la même fréquence (ondes cohérentes) interfèrent ; c’est-à-dire que l’observateur perçoit la superposition de ces deux ondes. Deux cas extrêmes sont possibles (figure 11) :
Les interférences sont constructives si les ondes sont en phases. L'amplitude de la résultante est alors maximale.
Les interférences sont constructives si δ = k × λ (avec k appartient à ℤ) : la différence de marche correspond à un nombre entier de longueur d’onde.
Les interférences sont destructives si les ondes sont en opposition de phase. L'amplitude de la résultante est alors minimale.
Les interférences sont destructives si δ = (2k+1) × λ/2 : la différence de marche correspond à un multiple impair d’une demi longueur d’onde.
Figure 11. Interférences constructives et destructives
Pour que des interférences aient lieu dans le domaine du visible (400 nm à 800 nm) et que des couleurs apparaissent, il faut que la différence de marche soit de l’ordre de grandeur de la longueur d’onde. Par conséquent, l’épaisseur du film de savon (e = δ / 2n) doit aussi être de l’ordre de l’ordre de grandeur de la longueur d’onde.
- L'épaisseur de la bulle
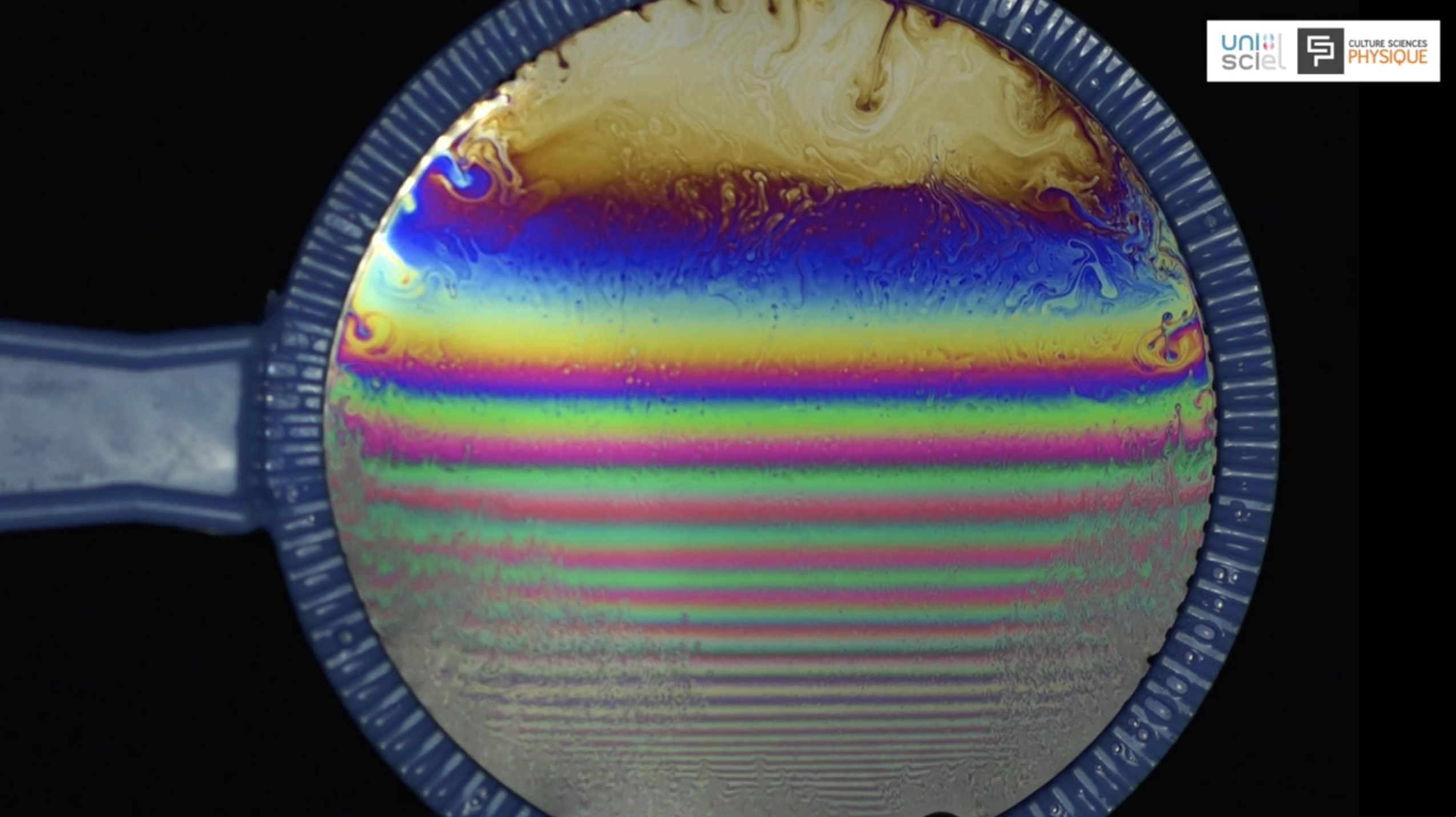
L’écoulement dans le film savonneux (phénomène de drainage) fait que l’épaisseur n’est pas la même sur toute la surface du film. Les franges colorées n’auront donc pas la même largeur sur toute la figure d’interférence.
Chaque radiation crée une figure d’interférence. La superposition des différentes figures d’interférences correspond à l’irisation.
Pour déterminer une estimation de l’épaisseur du film savonneux, nous avons utilisé l'échelle de couleur de Newton-Levy, figure 12.
Le haut de la bulle commence à noircir, juste avant son éclatement ce qui correspond à une épaisseur quasi-nulle. À partir de là, la succession des couleurs permet de déterminer la différence de marche δ = 2ne par lecture sur l’échelle.
L’indice de réfraction du milieu n est estimé à environ 1,3 (celui de l’eau) ce qui permet de déduire le profil d’épaisseur du film savonneux.
Nous utiliserons, dans la suite des calculs, une épaisseur de film correspondant au milieu de la bulle de e = 0,8 µm
Figure 12. Échelle de Newton-Levy
On pourra consulter la vidéo de La physique animée sur l'irisation d'une bulle de savon, pour retrouver plus en détail ces phénomènes d'interférences.
- Dynamique de la bulle
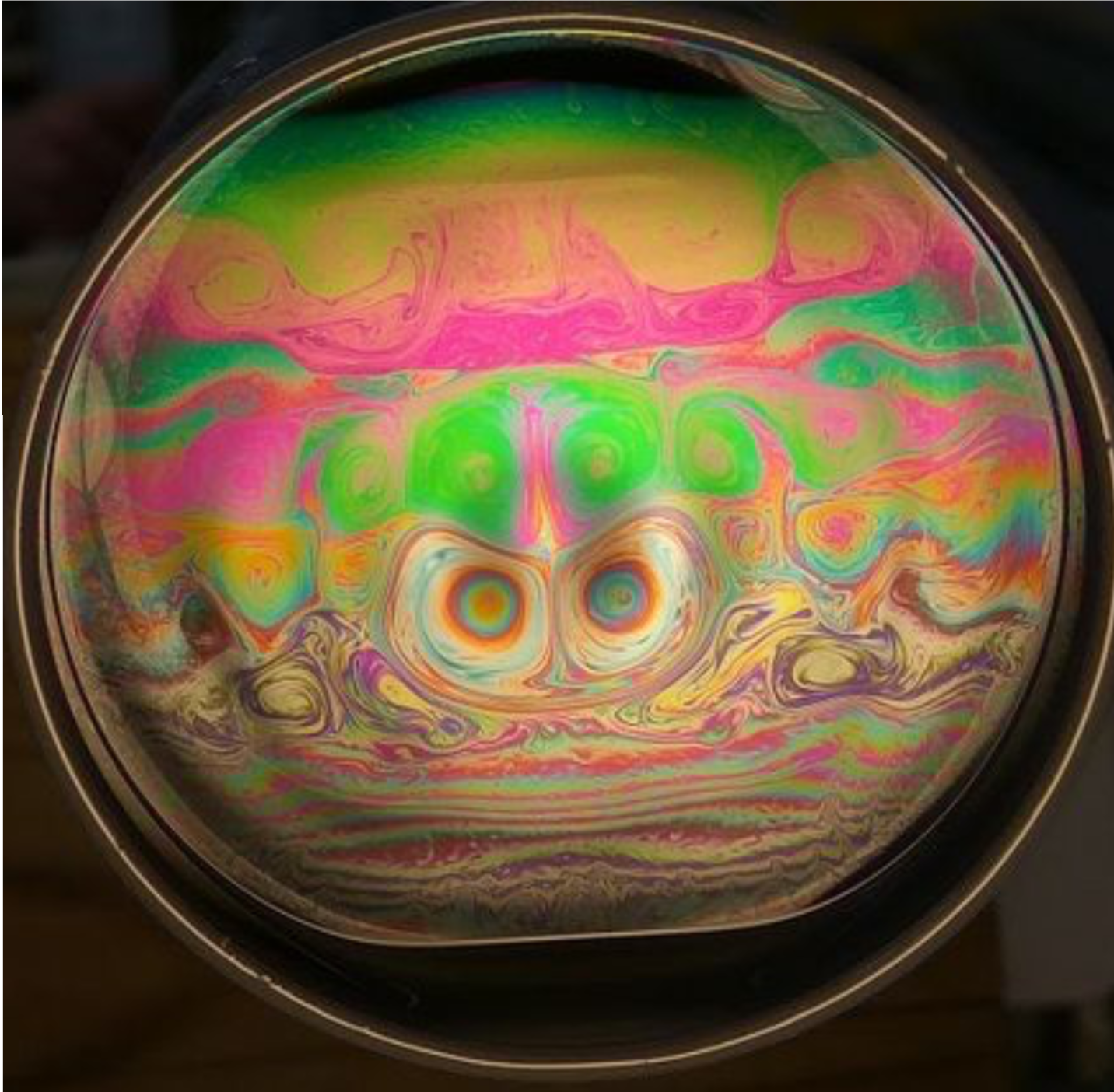
Au cours de notre expérimentation, nous avons alors remarqué que les couleurs présentes sur la bulle de savon formaient des vortex pour certaines fréquences uniquement. Par exemple la musique du groupe ACDC Back in black permet de faire apparaître des vortex.
Lorsque certaines conditions sont respectées, on remarque la création de tourbillons visibles grâce aux couleurs sur le plan du film de savon, figure 14. Ils résultent de l’impact d’un jet d’air sur le film savonneux. Ce jet d’air est en incidence normale par rapport au plan du film. L’écoulement de l’air se fait par la tangente au film et entraîne du liquide présent vers l’interface liquide-gaz qui se trouve loin du point d’impact du jet d’air. Cet écoulement est donc différent au niveau du point d’impact. Les tensioactifs constituant l’interface sont entraînés et ils créent un gradient de tension de surface. Par la suite un contre-écoulement du liquide arrive au niveau du point d’impact du jet d’air peu de temps après la mise en place du gradient de tension de surface. Les vortex observés naissent de ces écoulements de directions opposées.
3. Les ondes de surface
Lorsqu’on modifie la fréquence du GBF, on remarque que certaines fréquences sont amplifiées et qu’il apparaît sur la bulle de savon des ondes de surface concentriques.
3.1 Qu'est-ce qu'une onde capillaire ?
Une onde capillaire est une onde élastique qui se propage uniquement à la surface d’un matériau élastique, le film savonneux.
La propagation des ondes de surface, que ce soit pour des courtes ou des grandes longueurs d’ondes, est soumise à la tension superficielle. Cette tension superficielle est négligeable pour les grandes longueurs d’ondes. En revanche, pour les courtes longueurs d’ondes (de l’ordre du centimètre et une amplitude de l’ordre du millimètre), la tension superficielle domine la propagation des ondes de surface et engendre la création d’ondes appelées rides capillaires.
Générée sous la force acoustique et par les vibrations de l’air dans le tube qui imposent un mouvement transversal, l’onde capillaire est une onde vibratoire transversale qui se propage le long de la membrane liquide du film savonneux.
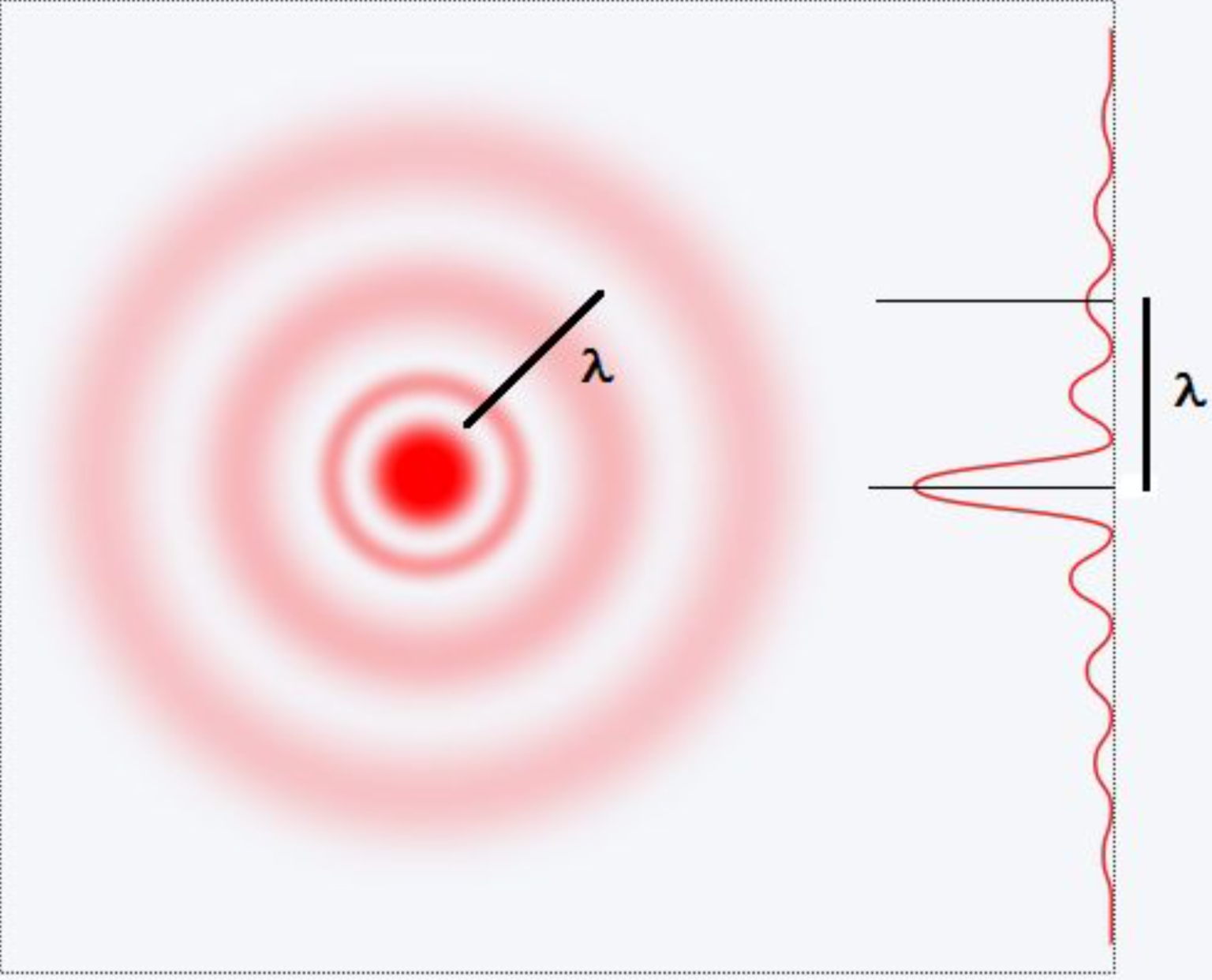
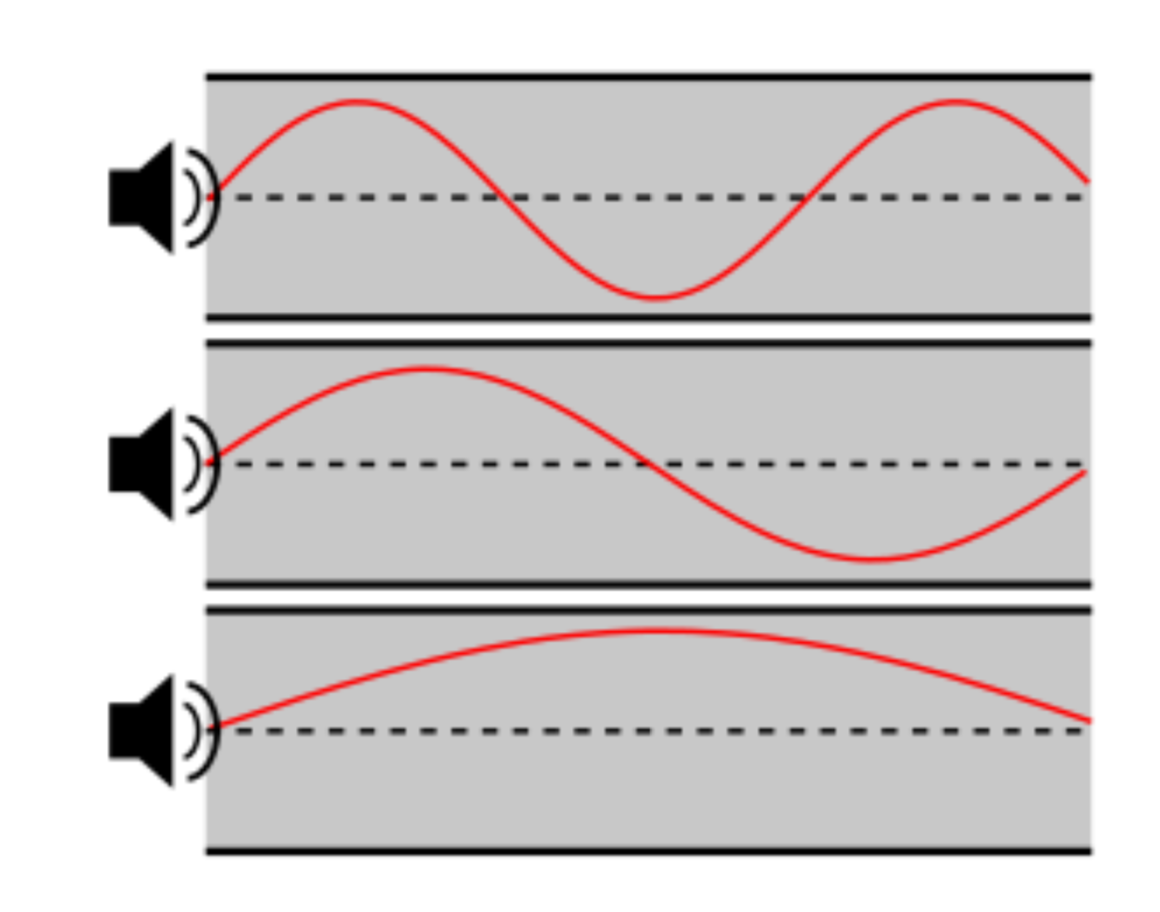
Les ondes se reflètent aux limites du film et en son centre. En raison de la symétrie axiale du tube, ceci conduit à l’apparition de cercles concentriques correspondants à une onde stationnaire. La fonction mathématique de cette onde correspond au profil de Bessel, figure 15.
Ces ondes capillaires apparaissent de manière amplifiée pour certaines fréquences, appelées fréquences de résonance du tuyau, que nous allons mettre en évidence à l’aide du dispositif de Kundt, figure 16.
Le tube de Kundt, du nom de son inventeur August Kundt, est également appelé appareil à ondes stationnaires. C’est un simple tube en plexiglas qui peut être ouvert (comme dans nos expériences) ou fermé, long ou court. Ce dispositif permet de mettre en évidence les ondes stationnaires sonores dans un tube rempli d’air.
Figure 16. Schéma du tube de Kundt
3.2 L'onde stationnaire
L’onde issue du haut-parleur et celle réfléchie à l’extrémité se superposent et forment une onde stationnaire.
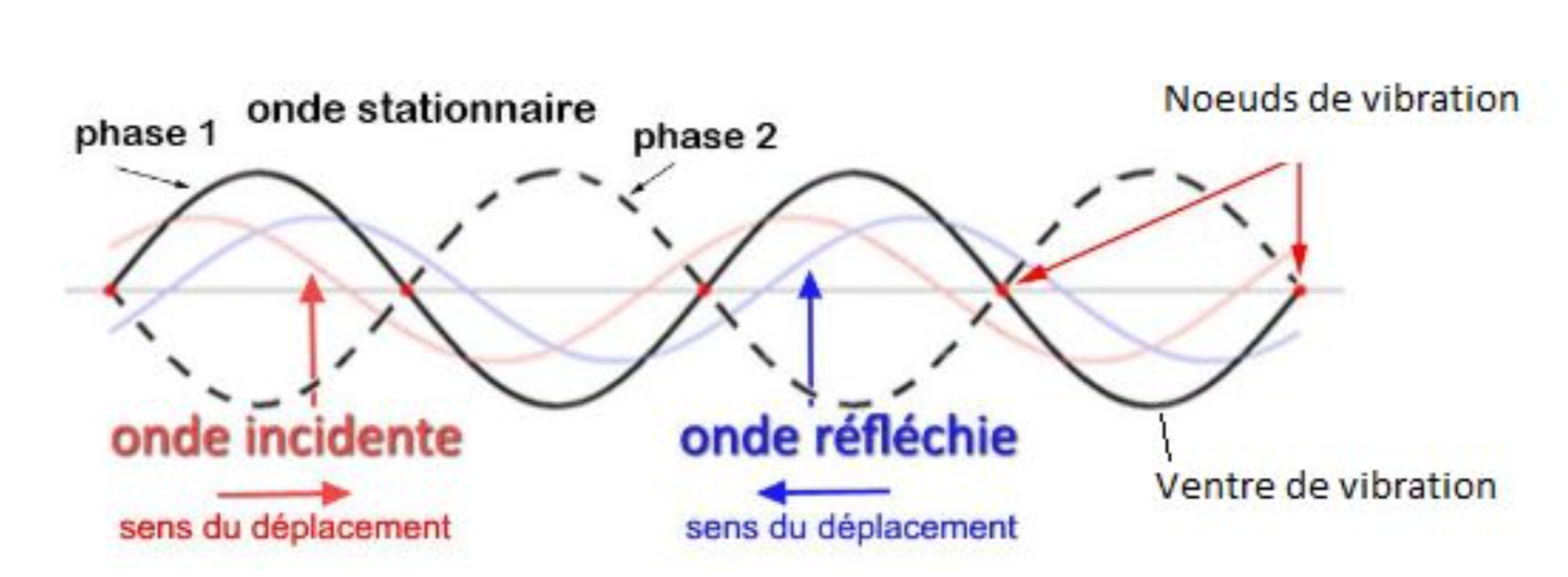
L'onde stationnaire est la superposition de deux ondes progressives de même fréquence mais de sens de propagation opposé dans le même milieu physique : l’air. La propagation simultanée de plusieurs ondes forme alors une figure dont certains éléments sont fixes dans le temps. Ainsi, au lieu de voir une onde qui se propage, on constate une vibration stationnaire mais d'intensité différente, en chaque point observé. Les points d’amplitude maximale sont les ventres de vibration et les points fixes sont les noeuds de vibration, figure 17.
Figure 17. Représentation d'une onde stationnaire
On pourra consulter la vidéo de La physique animée sur la mise en évidence expérimentale d'ondes stationnaire , à l'aide du tube de Rubens.
3.3 Les fréquences de résonance
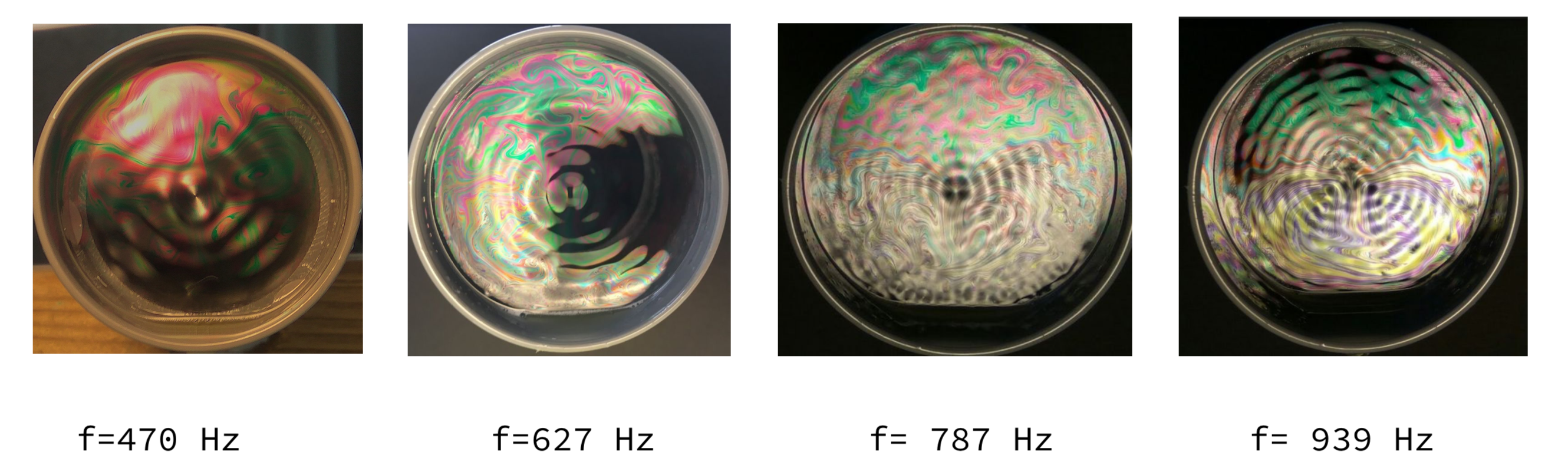
Seules certaines fréquences permettent d’observer le phénomène de résonance. Nous avons déterminé ces fréquences en recherchant l’apparition d'ondes capillaires sur la bulle. Nous avons obtenu les valeurs suivantes :
Valeurs expérimentales des fréquences (lues sur le GBF) | 470 Hz | 627 Hz | 787 Hz | 939 Hz |
La première fréquence de résonance mesurable dans de bonnes conditions correspond à la 3ème harmonique.
Ainsi, les fréquence de résonance correspondent à où n est un nombre entier naturel, ν est la vitesse de propagation de l’onde mécanique, L la longueur. Dans les conditions de température (23°C) et de pression, on a ν = 343 m/s
Valeur théorique de résonance | = 163 Hz | 327 Hz | 490 Hz | 653 Hz | 816 Hz | 980 Hz |
Nous remarquons que les valeurs théoriques ne correspondent pas totalement à nos mesures. Nous avons essayé d’identifier la cause ci-dessous.
3.4 Calculs expérimentaux
À l’aide d’un logiciel appelé SalsaJ (qui permet des mesures sur photos à l’échelle), nous avons pu déterminer la longueur d’onde associée à une fréquence de résonance : en effet il existe un lien entre la longueur d'onde des ondes capillaires et la fréquence de résonance. Pour se faire nous avons suivi le protocole suivant :
- Nous avons d’abord pris plusieurs photographies des ondes capillaires à la surface de la bulle.
- Nous avons tracé à l’aide du logiciel un repère pour représenter le diamètre du tube d’une longueur de 50 mm. Il donnera l'échelle.
- Nous mesurons une longueur d’onde ou plus.
D’après la thèse « Sound and vision : visualization of music with a soap film » de Camille Gaulon (doctorante en acoustique physique), la célérité ν a pour formule l’équation suivante :
Soit :
Donc :
Avec, dans les conditions de température et de pression, la tension superficielle γ = 35 mN/m ; la densité de l’eau ρeau = 997 kg/m3 ; la densité de l’air ρair = 1,204 kg/m3 ; l’épaisseur du film e = 0,8 µm.
Figure 18, dans le premier cas, nous avons mesuré une longueur d’onde de λ = 0,90 cm = 0,90.10-2 m pour 470 Hz imposés avec le GBF.
= 451 Hz
Nous avons répété ce calcul pour les autres photos.
λ = 0,90 cm | λ = 0,70 cm | λ = 0,62 cm | λ = 0,52 cm | |
Valeurs théoriques de f (d'après le calcul) | 451 Hz | 641 Hz | 757 Hz | 963 Hz |
Valeurs expérimentales de f (d'après la lecture sur le GBF) | 470 Hz | 627 Hz | 787 Hz | 939 Hz |
Écart relatif | 4% | 2% | 4% | 3% |
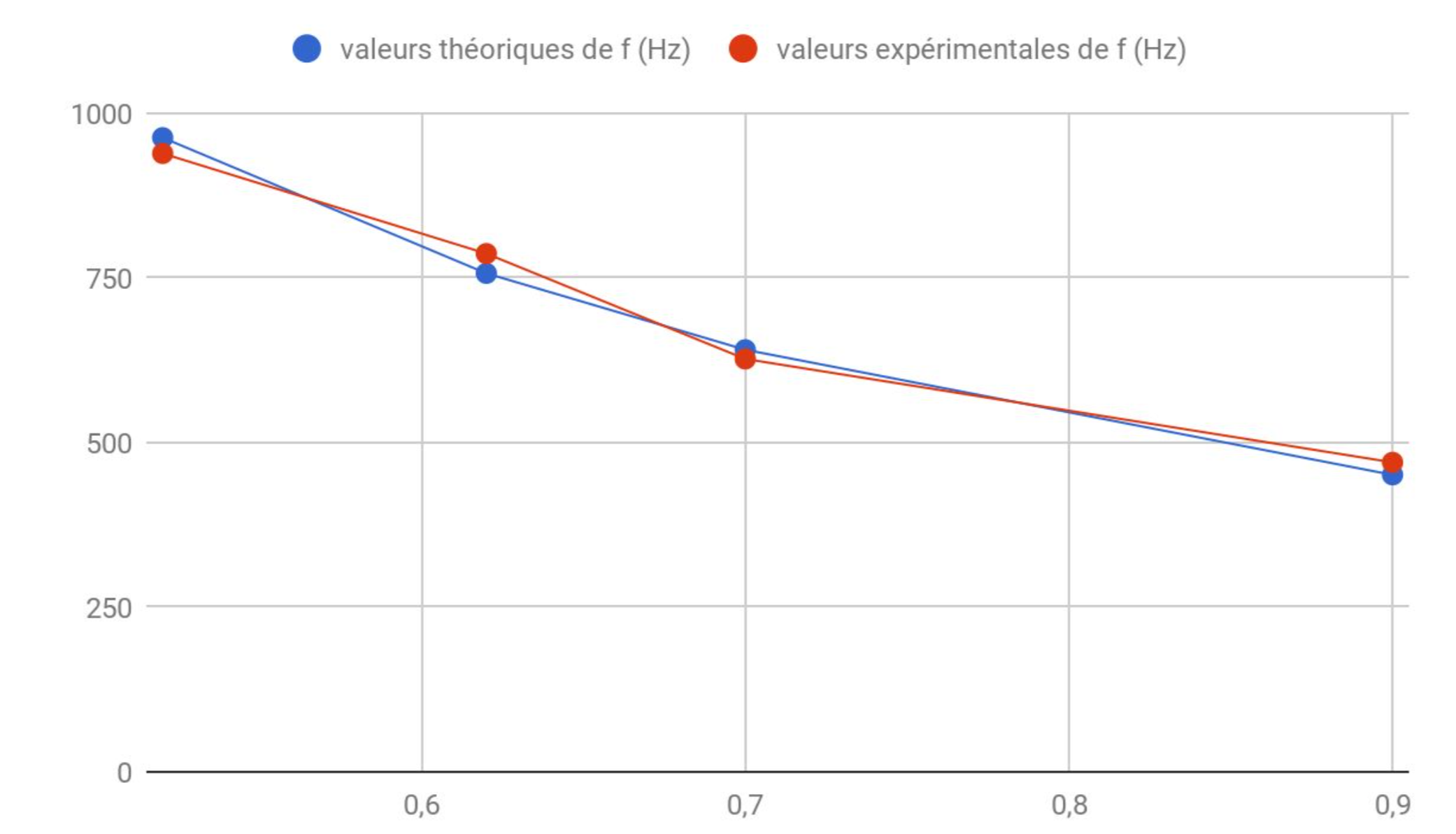
On observe une bonne concordance entre les valeurs expérimentales et théoriques, figure 19.
Nous avons échangé avec Camille Gaulon qui nous a orienté sur une amélioration de la formule des fréquences de résonance. En effet, il existe un facteur de correction C comme indiqué ci-dessous :
Ici, n est un nombre entier naturel représentant l’harmonique de rang n, ν = 343 m/s la célérité du son dans l’air, L la longueur du tube égale à 1,05 m.
Cette relation permet de calculer la fréquence de résonance en prenant compte du facteur de correction C, en mètre, permettant de faire le lien entre les valeurs théoriques et les valeurs trouvées. Ce facteur de correction prend en compte, entre autres, le diamètre D du tuyau. La relation trouvée dans la littérature[1] est C = 0,4×D.
Ainsi, dans notre expérience C = 0,4 × 50 mm = 0,2 cm.
Valeurs expérimentales des fréquences de résonance (d'après la lecture sur le GBF) | 470 Hz | 627 Hz | 787 Hz | 939 Hz |
Fréquences de résonance calculées sans correction : | 490 Hz | 653 Hz | 816 Hz | 980 Hz |
Fréquences de résonance calculées avec correction : | 472 Hz | 629 Hz | 785 Hz | 942 Hz |
Nous remarquons que, grâce à ce facteur de correction, nous nous approchons des valeurs expérimentales trouvées.
Par la suite, nous pourrions réaliser la même expérience mais avec un tuyau de même diamètre mais de longueur différente pour vérifier que l’introduction de ce facteur de correction entraîne une meilleure prévision des valeurs des fréquences de résonance.
Cette démarche expérimentale nous a permis de montrer le lien entre la longueur d’onde d’une onde de surface et la fréquence d’un son dans le tuyau. Nous nous sommes demandées si l’on pouvait utiliser ce phénomène dans un cas pratique : accorder un instrument de musique avec les yeux.
4. Vérifier l’accord d’un instrument visuellement
Mode opératoire :
Nous avons relié une guitare électrique au haut-parleur fixé au tube. La note émise par la corde doit correspondre à une fréquence de résonance du tuyau pour utiliser notre étude.
Dans notre cas, nous avons joué la note mi2 bémol, soit une fréquence de 156 Hz.
La fréquence théorique de l’harmonique de rang 1 pour notre tube est de 163 Hz qui correspond à une fréquence corrigée de 157 Hz soit très proche de la valeur du mi2 bémol.
Il apparaît alors sur le film de savon une onde capillaire, figure 20.
A l’aide du logiciel SalsaJ, nous avons déterminé la longueur d’onde de cette onde de surface, figure 21.
On trouve λ = 18,8 mm, donc par calcul de la fréquence :
= 157 Hz, comme attendu.
6. Conclusion
Pour conclure, nous avons réussi à visualiser le son en observant la danse des vortex, des ondes capillaires mais aussi des figures d’interférences hautes en couleurs.
Nous avons remarqué que pour une fréquence appelée fréquence de résonance, il se forme une onde de surface d’où nous pouvons extraire une longueur d’onde nous permettant de remonter jusqu’à la fréquence du son.
Ces différents phénomènes physiques nous ont donné la possibilité d’utiliser ce dispositif pour accorder une corde de guitare.
Pour aller plus loin, notre ensemble expérimental peut être également utilisé pour les malentendants. En effet, pour eux, le simple fait d’écouter de la musique leur est difficile d’accès. Cependant, à l’aide de notre dispositif, ils peuvent découvrir la musique d’une toute autre manière… à travers leurs yeux ! Ainsi, grâce aux propriétés d’iridescence de la bulle avec la danse des vortex et des ondes capillaires, ils éprouvent les sentiments et les émotions qui nous animent lors de l’écoute d’un morceau de musique.
7. Remerciements
- Nous tenons tout particulièrement à remercier Camille Gaulon, doctorante en acoustique physique, qui a répondu à nos multiples mails avec patience et gentillesse pour nous guider dans la réalisation de notre expérience.
- Merci également à Madame Touron, professeur d’anglais qui nous a éclairé sur les passages ardus de la thèse de Camille Gaulon rédigée en anglais.
- Nous remercions le personnel du laboratoire du Lycée Germaine Tillion et surtout Christine qui nous a apporté d'excellents conseils pour l’élaboration de cette expérience demandant une certaine préparation.
- Nous adressons nos remerciements à l’ensemble du Comité d'organisation des sciences à l’école qui nous a donné l’opportunité de nous intéresser de manière différente à un phénomène physique.
- Pour terminer, le plus important pour nous est d’exprimer notre gratitude la plus sincère à nos professeurs de Physique-Chimie du lycée Germaine Tillion, Madame Alleg et Monsieur Mathiotte pour tout le temps qu’ils nous ont accordé et l’aide précieuse qu’ils nous ont apportée en nous accompagnant dans la réalisation de notre projet.
Toutes ces personnes ont contribué à faire de ce projet une expérience enrichissante et agréable.
Pour citer cet article :
Onde sonore sur film de savon , Anna Brossier Ropital, Manon Pouilly et Léa Viallon, septembre 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/ondes-capillaires.xml
Pour citer cet article :
Onde sonore sur film de savon, Brossier Ropital, Pouilly, Viallon, septembre 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/ondes-capillaires.xml