Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
La structure du Monde - La nouvelle astronomie (3/3)
19/06/2017
Résumé
Développements en mathématiques et en physique aboutissant à une description physique du monde et à la mise en évidence, sur Terre, des mouvements orbitaux et de leurs effets.
Table des matières
Articles de la série « La structure du Monde » :
Le système géocentrique développé par Eudoxe et Aristote au IVe siècle av. J.-C. et parachevé par Ptolémée au IIe siècle ap. J.-C. est un système extrêmement cohérent, qui mêle d'une manière inextricable la physique et la structure du Monde (cf. Du cosmos des mythologies au géocentrisme). Il repose sur quatre idées fortes : 1) la théorie des lieux et des mouvements naturels entérine un clivage essentiel entre la Terre et le Ciel ; 2) la Terre est sphérique et immobile, elle coïncide avec le centre du Monde ; 3) le Monde est sphérique et clos ; 4) les astres sont portés par des sphères matérielles, qui ont naturellement un mouvement de rotation uniforme. En 1543, Nicolas Copernic (1473-1543) renverse les hiérarchies en mettant la Terre en mouvement et en plaçant le Soleil au centre (cf. Du géocentrisme à l'héliocentrisme). Un pas essentiel est effectué mais il est encore limité puisque Copernic ne fait tomber que la deuxième des idées d'Aristote en conservant toutes les autres. D'autres viennent après lui qui complètent ses travaux. À la fin du XVIe siècle, Tycho Brahé (1546-1601) réfute l'existence des sphères matérielles et contredit ainsi une autre idée fondamentale d'Aristote. Dans cet article[1], nous allons voir qu'au cours du XVIIe siècle tous les autres principes cosmologiques d'Aristote sont attaqués et abandonnés grâce aux travaux de Thomas Digges (v. 1546-1595), Giordano Bruno (1548-1600), Johannes Kepler (1571-1630), Galileo Galilei (1564-1642), René Descartes (1596-1650) et Isaac Newton (1642-1727). Il y a passage d'un univers conceptuel à un autre univers conceptuel, où tout est repris avec un point de vue différent. Un monde entièrement nouveau émerge.
Un Monde infini, rempli de soleils
Les étoiles circumpolaires décrivent chaque nuit autour du pôle céleste immobile des arcs de cercle d'autant plus grands qu'elles sont plus éloignées du pôle céleste. Cette observation suggère très fortement l'idée que toutes les étoiles sont situées à la même distance et réparties à la surface d'une sphère enveloppant la Terre et tournant en bloc. Si ce mouvement d'ensemble n'est pas un mouvement réel mais un mouvement apparent résultant de la rotation propre de la Terre sur elle-même dans le sens inverse alors la disposition sphérique des étoiles ne s'impose plus. En 1543, Copernic conserve l'idée de la sphère stellaire en la supposant fixe et c'est l'Anglais Thomas Digges qui saute le pas en 1576 : il affirme que les étoiles sont disséminées dans tout l'espace et que l'univers est infini. Le Monde clos et sphérique d'Aristote est abandonné. L'idée est reprise en 1584 par l'"Italien" Giordano Bruno, qui affirme également que toutes les étoiles sont des soleils, chacun entouré de planètes [réf1, p.54] : « Il [Dieu] ne se glorifie pas dans un seul, mais dans d'innombrables soleils, non pas en une seule terre, et un monde, mais en mille mille, que dis-je ? une infinité [de mondes] ».
Figure 1. Les étoiles ne sont plus réparties à la surface d'une sphère mais disséminées dans l'espace
Illustration de A Perfit Description of the Caelestial Orbes (Thomas Digges, 1576).
Les mouvements elliptiques de Kepler
Le principal artisan de la nouvelle astronomie, celui qui rejette au prix d'un travail acharné le principe deux fois millénaire du mouvement circulaire uniforme est l'"Allemand" Johannes Kepler. Personnalité singulière, doué de qualités hors du commun, son approche de l'astronomie est originale : il cherche non plus seulement à décrire géométriquement le système solaire et les mouvements planétaires mais il veut comprendre leurs structures internes, leurs causes profondes. Convaincu par les thèses coperniciennes grâce à l'enseignement de son maitre "allemand" Michael Mästlin (1550-1631), il veut faire le lien entre la géométrie et la physique et trouver les trajectoires des corps célestes en analysant les forces qui les meuvent sur leurs orbites, persuadé que celles-ci sont d'origine magnétique et qu'elles émanent du Soleil. Il est ainsi le premier à passer de la cinématique à la dynamique. Cette nouvelle approche est présente dès son premier ouvrage, Le Secret du monde, paru en 1596, ouvrage dans lequel il croit percer les secrets du système solaire en intercalant des polygones puis des polyèdres réguliers entre les orbes planétaires.
Figure 2. Johannes Kepler (1571-1630)
Copie d'un tableau original. Artiste inconnu.
La reprise puis l'abandon de l'équant et la découverte de la loi des aires
C'est une fois qu'il rencontre Tycho Brahé au début de l'année 1600 (année où l'Église brulait Giordano Bruno en place publique pour hérésie) et qu'il accède à ses formidables données d'observation de la planète Mars, que Kepler peut donner sa pleine mesure. Il reconnait le principe copernicien selon lequel les planètes se déplacent d'autant plus lentement qu'elles sont loin du Soleil mais il l'étend au déplacement des planètes individuelles sur leur orbite : puisque la distance d'une planète au Soleil varie alors, nécessairement, sa vitesse orbitale varie également. La conception dynamique des mouvements planétaires fait sauter un premier verrou de la tradition astronomique, celui de la nécessité des mouvements uniformes. Ce qui permet à Kepler de réintroduire l'équant que les astronomes arabes et Copernic s'étaient donnés tant de mal à faire disparaitre (l'équant est un point décalé du centre du cercle décrit par la planète et autour duquel la planète tourne uniformément, voir Figure 11 de Du cosmos des mythologies au géocentrisme) ! Pour Kepler, l'équant est la représentation mathématique de l'action physique de la force émanant du Soleil.
À ce stade, Kepler est encore persuadé que les orbites sont circulaires. Il élabore un premier modèle pour la planète Mars en supposant qu'elle décrit un cercle excentrique au Soleil et que son mouvement est réglé par un équant. Après des calculs bien fastidieux qu'il doit sans cesse reprendre, son modèle reste insatisfaisant : pour certaines positions de Mars sur son orbite, le désaccord entre le modèle et les données d'observation atteint 8' (' = minute d'arc) ce qui, compte tenu de la précision des mesures de Tycho Brahé, n'est pas acceptable. Ce sont ces 8' d'écart, parce qu'elles ne peuvent pas être négligées et qu'elles obligent Kepler à reprendre encore une fois ses recherches, qui vont ouvrir la voie à la réforme complète de l'astronomie. Cette opiniâtreté exceptionnelle de Kepler met en évidence une autre de ses convictions profondes : il ne peut se contenter d'un "à peu près" parce qu'il est persuadé que la construction divine du cosmos, qui est transposable mathématiquement, est parfaite. Le plan Divin ne sera saisi que lorsque l'accord entre la théorie et l'observation sera absolument rigoureux.
Kepler pressent que la distance de la planète au Soleil joue un rôle dynamique de toute première importance. Il abandonne l'équant et postule que la vitesse d'une planète est inversement proportionnelle à sa distance au Soleil (cette loi est juste à l'aphélie et au périhélie mais fausse dans le cas général). Ce qu'il s'efforce de trouver, c'est la loi donnant le temps que met une planète à parcourir l'arc AB de son orbite. Gapaillard explique (Figure 3) [réf3, p.151] : « Comme la distance de la planète P au Soleil S est variable, Kepler partage l'arc AB en une somme de n petits arcs P0P1, P1P2, …, Pn-1Pn, de longueurs égales, P0 et Pn, étant confondus avec les extrémités A et B [Figure 3]. Si l'on néglige la différence des longueurs SP0 et SP1, la vitesse de la planète le long de l'arc P0P1 est pratiquement constante et inversement proportionnelle à SP0, de sorte que le temps de parcours de P0P1 est proportionnel à SP0. De même, le temps de parcours de P1P2 est proportionnel à SP1 (avec la même constante de proportionnalité), etc. Finalement, le temps de parcours de l'arc AB est proportionnel à la somme SP0 + SP1 + … + SPn-1. Kepler sait bien que ce raisonnement est d'autant valable que les arcs P0P1, P1P2, …, Pn-1Pn sont plus petits, donc que leur nombre n est plus élevé. Malheureusement, quand n croît, la somme ci-dessus tend vers l'infini ! Kepler écarte alors cette grave difficulté par un artifice qu'il ne peut justifier mathématiquement et dont l'audace ne lui échappe pas : quand n devient très grand, il remplace la somme SP0 + SP1 + … SPn-1 par l'aire du secteur SAB (raisonnement qui n'est pas sans rappeler, avant l'heure, le calcul intégral d'une surface). La loi du mouvement devient : pour une planète donnée, le temps de parcours de l'arc AB de son orbite est proportionnel à l'aire du secteur SAB. C'est la célèbre loi des aires ou deuxième loi de Kepler – bien qu'elle fût découverte la première ».
Source - © 2017 D'après J. Gapaillard [réf3, p. 150]
Figure 3. L'idée de la loi des aires
L'abandon du cercle et la découverte des orbites elliptiques
En supposant toujours des orbites circulaires (le Soleil est bien sûr excentré), Kepler applique sa nouvelle loi des aires d'abord à la Terre, avec un très bon accord avec les observations, puis à Mars, où malheureusement les résultats sont moins bons. La loi des aires, qui remplace le mécanisme de l'équant, n'est qu'une première étape. Kepler en vient à douter des orbites circulaires et à supposer que la trajectoire de la planète est un ovale. Mais renoncer au cercle et trouver la forme exacte de l'ovale n'est pas chose facile. De son aveu même, c'est par l'épuisement des erreurs et des possibilités qu'il atteint la vérité. Il découvre qu'une trajectoire elliptique dont un foyer (le terme est de lui) coïncide avec le Soleil s'accorde parfaitement avec la trajectoire de Mars. C'est la première loi de Kepler. Mars est enfin capturé.
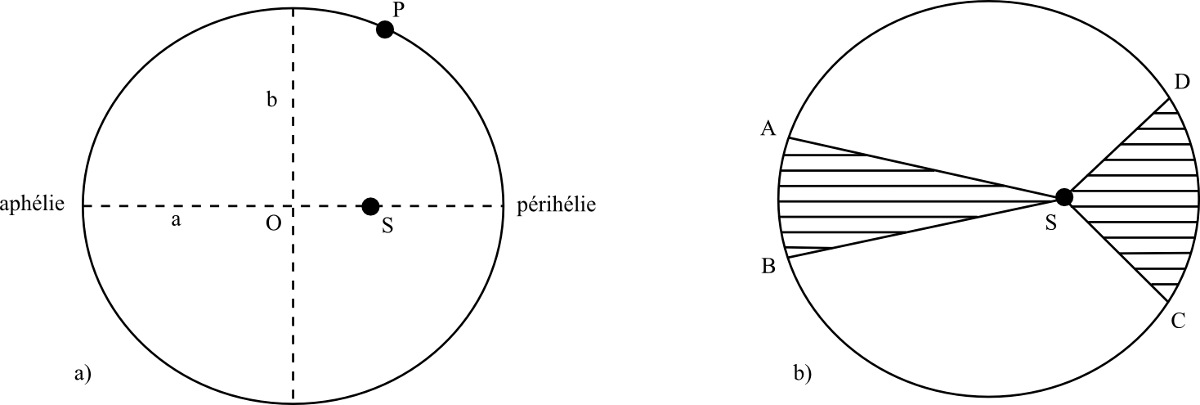
Les deux premières lois (Figure 4) sont publiées en 1609 dans son Astronomie nouvelle. Elles réforment l'ensemble de l'astronomie en rejetant les idées anciennes : les trajectoires ne sont pas circulaires mais elliptiques ; les mouvements ne sont pas uniformes et réglés par l'équant mais obéissent à la loi des aires, qui constitue un nouveau moyen de calculer les équations des mouvements planétaires. Les hypothèses sur lesquelles l'astronomie s'est construite depuis l'Antiquité sont complètement renversées.
Figure 4. Les deux premières lois de Kepler
a) La planète P décrit une orbite elliptique (de demi-grand axe a et de demi-petit axe b) dont le Soleil S occupe l'un des foyers.
b) La loi des aires : le rayon vecteur liant la planète au Soleil balaie des aires égales en des temps égaux.
L'unité du système solaire
Dans L'Harmonie du monde, paru en 1618, Kepler formule sa troisième loi : le carré de la période de révolution d'une planète est proportionnel au cube du demi grand axe de son orbite. Cette loi met en évidence le lien entre la vitesse de révolution d'une planète et sa distance au Soleil. Elle dévoile l'unité des mouvements planétaires au sein du système solaire.
La nouvelle science du mouvement de Galilée
La réfutation des idées aristotéliciennes est parachevée par l'"Italien" Galilée. Son propos est d'envergure : dans ses deux principaux ouvrages, Dialogue sur les deux principaux systèmes du Monde (1632) et Discours et démonstrations mathématiques concernant deux sciences nouvelles (1638), il entreprend à la fois une réfutation complète et systématique de tous les principes scientifiques et philosophiques d'Aristote, une justification de la thèse copernicienne en montrant que les mouvements de rotation et de révolution de la Terre ne sont pas incompatibles avec les expériences mécaniques de la vie quotidienne et la mise au point d'une nouvelle science mathématisée du mouvement.
Figure 5. Galileo Galilei, dit Galilée (1564-1642)
Extrait d'un portrait peint par Justus Sustermans, 1636.
Réfutation des idées aristotéliciennes
Le système aristotélicien est un système qui possède un haut degré de cohérence, où cosmologie et conception du mouvement sont parties liées. Mais s'il forme un ensemble où tout se tient, il suffit qu'une des pièces de l'édifice soit réfutée pour que la construction toute entière soit ébranlée. C'est sur la dichotomie entre la Terre et le Ciel que Galilée dirige ses premières attaques grâce à l'utilisation de la lunette astronomique. Les longues-vues constituées des deux lentilles apparaissent à la toute fin du XVIe siècle. Peut-être sont-elles inventées par un artisan opticien hollandais, Hans Lippershey (1570-1619) ou par un physicien italien, Giambattista Della Porta (1535-1615) (voir à ce sujet, La révolution scientifique n’est pas sortie de la lunette de Galilée). Elles se répandent rapidement en Europe au début du XVIIe siècle et lorsque leur propriété étonnante est confirmée, Galilée entrevoit immédiatement le parti qu'il peut en tirer. Il en construit lui-même pour essayer d'en améliorer la performance (Figure 6).
Figure 6. Les lunettes de Galilée
En novembre 1609, Galilée pointe sa lunette vers le ciel et, en l'espace de deux mois, il va aller de découverte en découverte. Il observe tout d'abord les montagnes lunaires : la surface de la Lune n'est ni lisse ni polie comme l'affirmait Aristote mais accidentée et inégale, comme la Terre. Des observations semblables, même si moins précises, étaient accessibles à Aristote et à tous les aristotéliciens qui lui ont succédé, mais ils privilégiaient la théorie et le modèle à l'observation et à l'expérience. En effet, chacun peut voir les taches claires et sombres sur la Lune (on y "reconnait" un visage en Europe, un lapin en Chine...), taches qui "prouvent" que la Lune ne pouvait être considérée comme un astre parfait, puisque l'interprétation de ces taches comme des reflets sur un astre parfait ne pouvait convenir du fait de la position relative variable entre Soleil, Terre et Lune, les taches ne pouvaient alors pas être immobiles. Quelques semaines plus tard, Galilée remarque les taches solaires, puis, à la suite d'observations minutieuses et poursuivies, il note leur mouvement sur la surface du Soleil, leurs variations et leurs altérations. Là encore, l'observation des taches solaires est possible à l'œil nu, et a même été reportée dès 164 av. J.C (Wittman, 1987 [réf7]) dans des textes chinois, même s'il faut la conjonction de deux événements particuliers : la présence de taches solaires "visibles" et d'un filtre naturel, comme une brume bien épaisse ou un voile nuageux adéquat, permettant l'observation du Soleil sans éblouissement. Ces premières observations instrumentées de Galilée confirment ce que Tycho Brahé avait déjà soupçonné : le monde céleste n'est pas aussi parfait et éternel que le supposait Aristote, mais il est sujet comme la Terre aux changements et aux variations. Galilée découvre également les phases de Vénus et la lumière cendrée de la Lune, ce qui dévoile l'identité entre la Terre et les planètes : comme la Terre, les planètes n'ont pas de luminosité propre mais elles ne brillent qu'éclairées par le Soleil ; comme les planètes, la Terre est apte à réfléchir la lumière solaire puisqu'elle éclaire la Lune (ce qu'on appelle la lumière cendrée, voir, par exemple, La Lune a rendez-vous avec Vénus ou La triple conjonction Lune-Jupiter-Vénus, 25-26 mars 2012). Galilée observe encore les satellites de Jupiter, montrant que tout ne tourne pas autour de la Terre et qu'un satellite peut être en mouvement autour d'une planète elle-même en révolution autour du Soleil. Toutes ces découvertes indiquent que le clivage entre la Terre et le Ciel, pierre angulaire du système aristotélicien, ne tient plus et qu'il y a unité entre les domaines céleste et terrestre. La conséquence est grande car l'unification physique du Monde fait perdre son fondement et sa justification à la théorie des lieux et des mouvements naturels d'Aristote. Ce sont alors tous les arguments philosophiques qui s'opposaient à l'héliocentrisme qui deviennent caducs.
Justification de l'héliocentrisme
Si l'héliocentrisme n'est plus interdit par les principes philosophiques, il reste à montrer que les mouvements de la Terre ne sont pas incompatibles avec les données d'observations. La situation est fort différente selon qu'il s'agit du mouvement annuel ou du mouvement diurne. Pour le mouvement annuel, le problème est celui de la détection d'une parallaxe annuelle. Galilée suppose que les étoiles sont disséminées dans tout l'espace. La parallaxe devrait se manifester par un déplacement périodique des étoiles proches relativement aux étoiles lointaines (Figure 7). Tycho Brahé se laissait abuser par la diffusion des images stellaires sur la rétine et pensait pouvoir attribuer une taille angulaire aux étoiles. Pour qu'aucune parallaxe ne puisse être mise en évidence, il fallait que les étoiles soient très éloignées du Soleil mais plus leur éloignement augmentait, plus il fallait leur conférer des dimensions qui défiaient l'imagination. Galilée invalide le raisonnement de Tycho Brahé en remarquant que les étoiles observées à travers la lunette astronomique sont perçues comme ponctuelles. Elles peuvent donc avoir des tailles modestes tout en étant suffisamment éloignées du Soleil pour que la parallaxe soit insensible.
Figure 7. La parallaxe annuelle des étoiles
Une étoile proche semble se déplacer sur le fond des étoiles lointaines en raison d'un effet de perspective dû à la révolution de la Terre autour du Soleil.
Pour lever les objections au mouvement journalier, Galilée se place résolument sur le terrain de la mécanique. Le problème principal est celui du lâcher d'une pierre depuis le sommet d'une tour. Si la Terre tournait, disent les partisans d'Aristote, la pierre ne pourrait jamais tomber au pied de la tour : le sol entrainé vers l'Est par la rotation de la Terre devrait se déplacer rapidement sous elle et la pierre devrait retomber bien à l'Ouest de son point de départ. Il n'en est rien, affirme Galilée, et pour le prouver il propose l'expérience suivante : si un homme est au sommet du mât d'un bateau qui se déplace en ligne droite et à vitesse constante sur une mer calme et sans vent et qu'il laisse tomber une pierre, où celle-ci va-t-elle arriver ? Au pied du mât ou alors bien à l'arrière du bateau, dans la mer ? Galilée explique que si l'on néglige le frottement de l'air, la pierre atterrit au pied du mât. En effet, lorsque la pierre est tenue dans la main de l'homme en haut du mât, elle a la même vitesse horizontale que le navire. La pierre, tout au long de sa chute, garde « imprimée en elle » cette vitesse horizontale et peut ainsi glisser le long du mât. Le même raisonnement peut être repris pour la pierre lâchée du haut de la tour. Que la Terre soit immobile ou en mouvement ne change rien à l'expérience : dans les deux cas, la pierre retombe au pied de la tour. L'erreur des partisans d'Aristote était de supposer que l'objet lâché partait du repos absolu et de ne pas considérer la vitesse horizontale communiquée par le navire ou la Terre en mouvement. Pour les phénomènes mécaniques se déroulant à la surface de la Terre, le mouvement diurne est donc comme s'il n'était pas, il reste insensible, imperceptible et ne semble avoir aucune action.
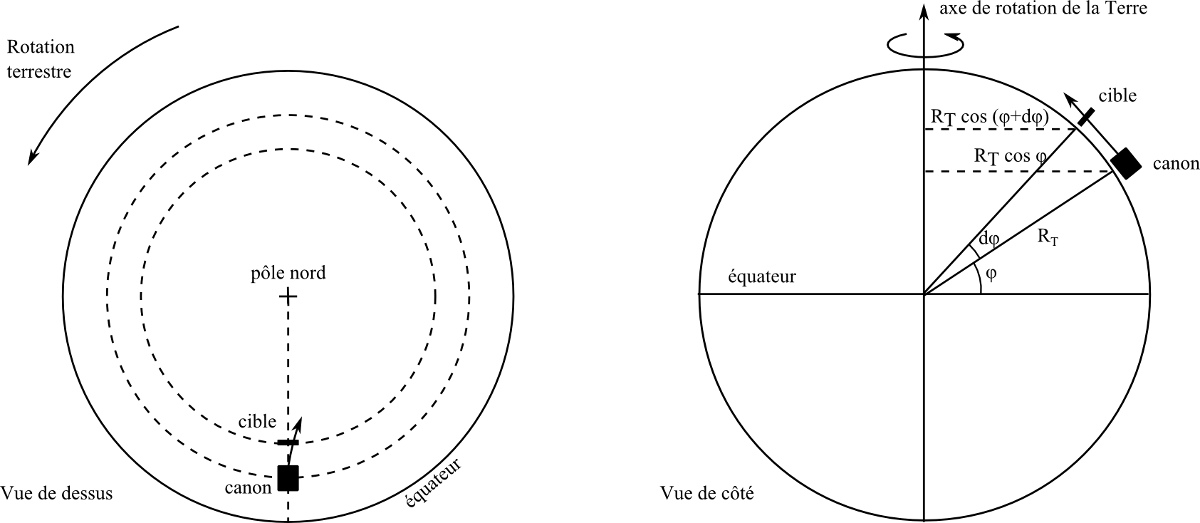
Mais, si plus rien ne s'oppose à la rotation de la Terre, dispose-t-on d'une preuve positive de son mouvement ? Galilée pense-t-il vraiment que les phénomènes mécaniques sont exactement les mêmes sur une Terre en rotation et sur une Terre immobile ? Quelques réflexions plus subtiles au sujet des mouvements à la surface du globe laissent penser le contraire. En analysant le tir du boulet de canon selon le méridien (Figure 8) ou selon la direction Est-Ouest (Figure 9), il s'aperçoit que la rotation de la Terre doit induire une faible déviation, malheureusement trop petite pour être confirmée par l'expérience. Il s'agit de la première prise en compte intuitive de ce qu'on appellera plus tard la force inertielle de Coriolis.
Figure 8. Le tir d'un boulet de canon vers le Nord est légèrement dévié vers l'Est
Le canon, situé au Sud de la cible, se trouve sur un parallèle de rayon un peu supérieur à celui du parallèle passant par la cible et se déplace vers l'Est légèrement plus vite. Pendant son vol, le boulet conserve la vitesse de translation vers l'Est du canon et progresse donc dans cette direction un peu plus vite que la cible.
On suppose que l'expérience a lieu à la latitude de φ = 45° et que le boulet met t = 2 s à atteindre la cible distante de l = 600 m. Le rayon de la Terre est RT, les vitesses vers l'Est du canon et de la cible sont vcanon et vcible, la vitesse angulaire de la Terre est et l'angle dφ est égal à l/RT.
Une estimation de la déviation est donnée par : . Comme dφ est un petit angle, . Il vient : .
Remarque : Les calculs proposés dans l'article ne servent qu'à donner une estimation des déviations rencontrées dans la chute des corps à la surface de la Terre. Ils supposent en effet que le sol est animé d'un mouvement de translation rectiligne, ce qui n'est pas juste. Pour obtenir les déviations exactes, il faut travailler dans un repère tournant avec la force inertielle de Coriolis.
Source - © 2017 D'après J. Gapaillard [réf3, p. 201]
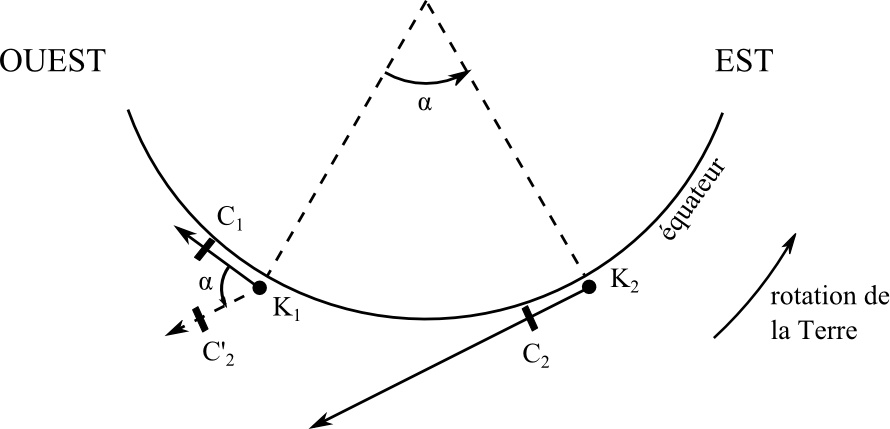
Figure 9. Le tir d'un boulet de canon vers l'Ouest est légèrement dévié vers le bas
L'expérience a lieu à l'équateur sur une cible distante de 300 m que le boulet met 1s à atteindre. En appliquant le principe de relativité, on peut faire abstraction de la translation vers l'Est du système canon-cible : tout se passe comme si ce système pivotait sur place autour du canon, à la vitesse et dans le sens de la rotation terrestre. Si le tir est déclenché quand la cible est en C1 et le canon en K1, la trajectoire du boulet est pratiquement la droite K1C1. Quand le boulet arrive au niveau de la cible, celle-ci se trouve en C2 et le canon en K2. Mais, comme rappelé ci-dessus, tout se passe comme si le canon était resté en K1 et que la cible avait pivoté autour de K1 pour se retrouvé en C'2. L'angle de rotation est l'angle dont la Terre a tourné pendant 1s, soit 15'' ('' = seconde d'arc). L'écart à la cible est de : .
La nouvelle science mathématisée du mouvement
En rejetant l'idée selon laquelle tout corps possède un lieu naturel qu'il revient occuper s'il s'en trouve éloigné, Galilée sépare nettement le mouvement de la constitution physique des corps. Il peut donc nier tous les fondements de la mécanique qualitative d'Aristote pour construire une nouvelle mécanique, basée sur l'imbrication étroite entre l'expérience et l'analyse mathématique. Le mouvement peut être étudié pour lui-même, non en référence à son rôle cosmologique. Dans son Dialogue en 1632 et ses Discours en 1638, il donne les premières lois mathématisées de la chute des corps et de l'oscillation des pendules.
S'il n'y a pas encore de mécanique céleste chez Galilée, s'il ne réussit pas réellement à trouver des preuves positives de la rotation et de la révolution de la Terre, si enfin son système, malgré toutes les avancées fécondes et les premières lois mathématisées du mouvement, contient encore bien des contradictions, la voie est néanmoins ouverte pour que la mécanique classique prenne la place de l'ancienne physique aristotélicienne.
La mécanique cartésienne
Descartes est le premier à tirer toutes les conséquences du rejet des doctrines antiques et à fonder une science universelle. La mécanique cartésienne est présentée dans Le Monde écrit en 1633 mais publié en 1644, après sa mort, pour ne pas risquer une condamnation religieuse. Son l'influence s'étendra sur l'Europe pendant plus d'un siècle. Même si elle pose sans doute plus de problèmes qu'elle n'en résout de manière satisfaisante, elle n'en possède pas moins plusieurs mérites. Elle représente une vaste synthèse, rationnelle, moderne dans le sens où elle intègre les aspects nouveaux de la révolution copernicienne. Elle est universellement applicable, c'est-à-dire qu'elle gouverne à la fois la Terre et les Cieux. Elle repose sur des principes simples et mathématiquement vérifiables : la loi de la conservation de la quantité de mouvement et la loi de l'inertie, que Descartes est le premier à énoncer clairement.
Le monde imaginé par Descartes est infini, sans vide et en constant mouvement. Une matière subtile remplit entièrement l'espace entre le Soleil et les planètes. Elle est organisée en d'énormes tourbillons imbriqués les uns dans les autres. Le tourbillon principal est mis en mouvement par la rotation propre du Soleil, qui en occupe le centre. Il emporte les différentes planètes sur leurs orbites. Comme la vitesse angulaire du tourbillon décroit au fur et à mesure de l'éloignement au Soleil en raison d'une sorte de friction, les planètes effectuent leur révolution autour du Soleil d'autant plus lentement qu'elles sont distantes du centre. La rotation propre des planètes génère des tourbillons secondaires qui entrainent les satellites. Dans le monde de Descartes, rien ne peut se déplacer sans être poussé ou tiré, chaque manifestation a une raison palpable. Pour connaitre la loi d'un phénomène, il faut d'abord en comprendre la cause. C'est une vision mécaniste de l'univers, où toute chose est régie par les seules lois du mouvement.
Figure 10. Les tourbillons de Descartes
Le cosmos est organisé en tourbillons ou cieux. L'espace FGGF est un ciel qui tourne autour du Soleil S, l'espace HGGH en est un autre qui tourne autour de l'étoile marquée "e".
Dans : René Descartes, Le Monde ou Traité de la Lumière, réimpression Paris, Vrin-CNRS, 1974.
La mécanique newtonienne
La mécanique développée par Newton est toute autre, elle poursuit les investigations de Galilée en évitant la mécanique cartésienne. Pour échafauder sa nouvelle mécanique, Newton s'appuie sur les travaux de ses contemporains : l'idée de l'attraction universelle est dans l'air (cf. encart ci-après), la loi de l'inertie a été donnée par Descartes, l'analyse correcte du mouvement circulaire a été faite par Robert Hooke (1635-1703) et l'expression de la force centrifuge a été donnée par Christiaan Huygens (1629-1695), même si Newton en fait une démonstration indépendante. Son immense mérite n'est pas d'avoir tout inventé mais d'avoir démontré quantitativement ses affirmations et d'en avoir tiré toutes les conséquences. Il publie ses découverte en 1687, dans ses fameux Principes Mathématiques de la Philosophie Naturelle. Sa mécanique repose à la fois sur des principes mathématiques simples, qui sont les trois lois du mouvement (la loi de l'inertie, la loi de l'impulsion et la loi de l'égalité de l'action et de la réaction), et sur l'attribution de certaines qualités aux corps : chaque corps est caractérisé par sa masse, ce qui précise un paramètre physique fondamental, la quantité de matière, et chaque corps possède une capacité d'attraction gravitationnelle sur les autres corps. Il explique que sa grande découverte n'est pas l'invention de la loi d'attraction en 1/r2 (r étant la distance entre les deux masses qui s'attirent) mais la démonstration des deux premières lois de Kepler (la troisième en étant une conséquence).
Figure 11. Isaac Newton (1642-1727)
La mécanique newtonienne permet une explication unifiée des mouvements dans le système solaire : les mouvements elliptiques des planètes autour du Soleil et des satellites autour des planètes sont la conséquence de la gravitation universelle. Elle parachève ainsi la révolution copernicienne en justifiant mécaniquement la thèse héliocentrique et en lui donnant la cohérence théorique qui lui faisait défaut. Outre les lois de Kepler, Newton explique les mouvements complexes de la Lune et donne des explications lumineuses à des phénomènes qui restaient sans explication satisfaisante, comme les marées ou la précession des équinoxes. Il prédit également que la forme de la planète n'est pas parfaitement sphérique mais ellipsoïdale, ce qui sera vérifié 50 ans plus tard (cf. La forme de la Terre : plate, oblongue ou aplatie aux pôles ?). La mécanique newtonienne amène donc un renouveau complet mais aussi un changement de nature dans la compréhension du Monde. D'un côté, il semble qu'elle fasse perdre une certaine forme d'explication par rapport aux thèses cartésiennes : des qualités « incompréhensibles » sont introduites là où chaque phénomène avait une cause précise et palpable. Le monde de contact de Descartes, où rien ne pouvait se mouvoir sans être entrainé par un tourbillon de matière est remplacé par quelque chose de « mystérieux », par des propriétés de la matière qui ne peuvent pas être expliquées : quelle est la nature de la force de gravitation, comment peut-elle agir à distance ? Mais d'un autre côté, la mécanique newtonienne permet de disposer d'un ensemble de lois mathématiques pouvant prédire et retrouver par le calcul un certain nombre de phénomènes. Elle rend possible une compréhension quantitative du Monde, là où la mécanique cartésienne n'offrait qu'une compréhension qualitative.
La réception des idées newtoniennes est très contrastée, entre la ferveur des Anglais et la grande hostilité des savants du continent européen. Le plus grand obstacle à la diffusion de ses idées est sa conception de la gravitation universelle, comprise comme une action à distance. Mais peu à peu, les problèmes métaphysiques sur le bien fondé de l'attraction newtonienne sont mis de côté (même s'ils demeurent irrésolus) pour admettre la prééminence des calculs. Grâce à la mise au point du calcul différentiel et intégral, de nouvelles études d'envergure reprennent les théories newtoniennes à partir des années 1740. Elles portent sur les marées océaniques, la précession des équinoxes, la théorie de la Lune (orbite, inclinaison du plan de révolution...) et la forme de la Terre, et sont dues à Pierre Louis Moreau de Maupertuis (1698-1759), Daniel Bernoulli (1700-1782), Leonhard Euler (1707-1783), Jean le Rond D'Alembert (1717-1783), Alexis Clairaut (1713-1765) et Pierre Bouguer (1698-1758). Alors les idées newtoniennes peuvent triompher sans retenue.
Des preuves de la rotation et de la révolution de la Terre
Si la mécanique newtonienne corrobore le système héliocentrique et si ce dernier n'est plus mis en doute, existe-t-il des preuves directes de la rotation et de la révolution de la Terre ? Encore une fois, il faut distinguer le mouvement diurne et le mouvement annuel.
Les effets de la rotation journalière de la Terre
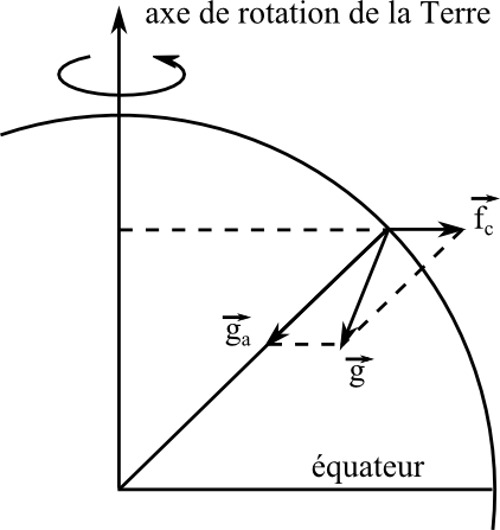
La rotation axiale de la Terre se manifeste d'un point de vue mécanique par l'intermédiaire de deux forces inertielles : la force centrifuge et la force de Coriolis. La force centrifuge agit perpendiculairement à l'axe de rotation. Elle est quantifiée par Huygens vers 1659 puis par Newton en 1665-1666. Elle est proportionnelle à la distance à l'axe et au carré de la vitesse angulaire. Elle s'ajoute vectoriellement à la gravité pour constituer la pesanteur (Figure 12). Son premier effet est de provoquer une diminution de l'intensité de la pesanteur avec la latitude : les corps ont un poids un peu moins grand sous l'équateur que sous les cercles polaires (cf. La découverte historique de la variation de la pesanteur avec la latitude). À l'époque, le moyen le plus sûr d'apprécier les variations de l'intensité de la pesanteur est fourni par le pendule, dont les oscillations sont d'autant plus lentes que l'attraction terrestre est faible. Jean Richer (1630-1698), envoyé à Cayenne en 1672 pour y observer la planète Mars, remarque qu'un pendule réglé à Paris y retarde de deux minutes et demie par jour. Le résultat est aussitôt interprété comme une marque assurée de la diminution de la pesanteur avec la latitude. Il constitue la première manifestation mécanique de la rotation terrestre.
Figure 12. Pesanteur, gravité et force centrifuge
La pesanteur est la somme vectorielle de la gravité et de la force centrifuge .
Aux pôles, la force centrifuge est nulle. À l'équateur, elle est maximale et elle s'oppose à la gravité.
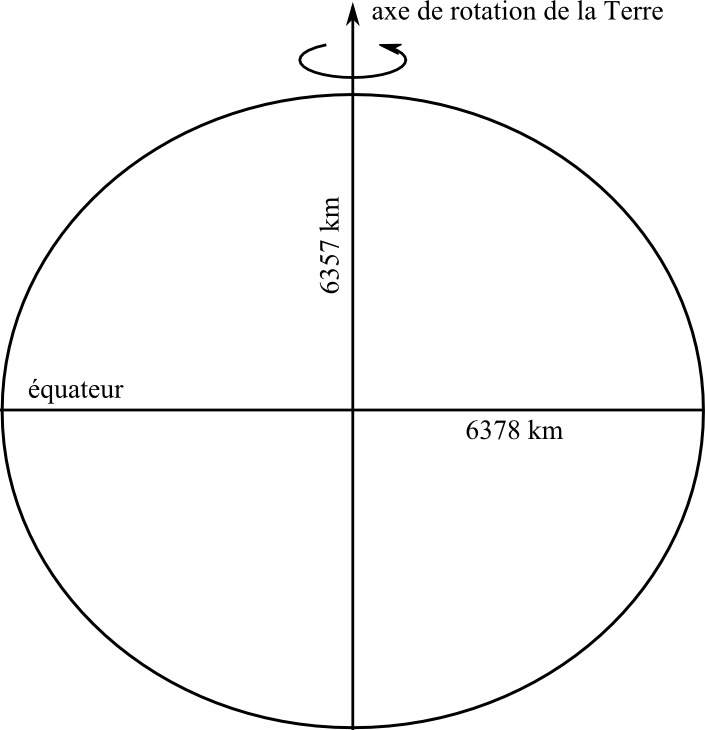
Le deuxième effet de la force centrifuge est de dévier la direction de la pesanteur. Cette dernière n'est pas dirigée exactement vers le centre de la Terre mais s'écarte légèrement vers l'équateur. Newton en déduit que si la Terre se comporte comme une masse fluide alors elle ne peut pas avoir une forme parfaitement sphérique mais elle doit avoir une forme ellipsoïdale, le rayon équatorial devant être légèrement plus grand que le rayon polaire. La Terre doit être aplatie aux pôles ! La vérification de cette prédiction soulève une fameuse controverse. Les premières mesures de la longueur d'un arc de 1° réalisées en France entre 1683 et 1718 semblent montrer une Terre allongée suivant son axe de rotation. Pour trancher la question, deux expéditions françaises sont envoyées au Pérou et en Laponie entre 1735 et 1744 pour y mesurer la longueur d'un arc de 1° à des latitudes très différentes. La thèse de Newton est validée : la Terre est bien aplatie !
Figure 13. Aplatissement de la Terre
La Terre n'a pas une forme exactement sphérique mais est aplatie aux pôles.
Le rayon équatorial est plus long que le rayon polaire d'une vingtaine de kilomètres.
La force de Coriolis agit sur les corps en mouvement et dévie leur trajectoire. Ses effets sont d'abord compris d'une manière intuitive avant d'être quantifiés correctement par Pierre Simon de Laplace (1748-1827) et Carl Friedrich Gauss (1777-1855) à la fin du XVIIIe siècle puis par Gustave Coriolis (1792-1843) au début du XIXe siècle. On a vu les réflexions pertinentes de Galilée sur le tir d'un boulet de canon vers le Nord ou vers l'Ouest. En 1679 Newton expose une nouvelle idée permettant de mettre en évidence le mouvement journalier de la Terre. Il explique qu'un objet lâché du haut d'une tour ne doit pas tomber à l'Ouest de la verticale passant par son point de lâcher comme le proclamaient les partisans d'Aristote, ni même exactement selon la verticale mais légèrement à l'Est ! En effet, avant sa chute, l'objet est plus éloigné de l'axe de rotation que la surface de la Terre qu'il surplombe et possède de ce fait une vitesse horizontale vers l'Est légèrement plus grande. Pendant sa chute, il garde son surplus de vitesse et atterrit un peu à l'Est de la verticale. Les premières vérifications expérimentales sont effectuées par Hooke en 1679 mais elles ne mettent en évidence aucune déviation probante. D'autres expériences sont réalisées au début du XIXe siècle, mais la dispersion des résultats est trop grande pour que ceux-ci soient pleinement concluants.
Figure 14. Déviation de la chute libre
On suppose que l'expérience a lieu à la latitude . Le rayon de la Terre est , la hauteur de la tour est , le temps de chute est , les vitesses vers l'Est du haut et de la base de la tour sont et , la vitesse angulaire de la Terre est . Une estimation de la déviation est donnée par :
.
Comme la hauteur et le temps de chute sont liés par (avec la pesanteur égale à 9,81 m.s-2), la déviation est :
.
Pour une hauteur de chute de 30 m, la déviation est de l'ordre de 5 mm.
En 1735, George Hadley (1685-1768) effectue un raisonnement similaire pour expliquer la direction des vents alizés. Avant lui, on rendait compte de l'orientation des alizés vers l'Ouest en supposant que l'air près de l'équateur ne pouvait pas suivre la grande vitesse de rotation de la Terre. Hadley explique que les particules d'air se dirigeant vers l'équateur subissent une déviation vers l'Ouest car elles survolent des terres situées plus loin de l'axe de rotation et ayant une vitesse vers l'Est plus grande. La rotation de la Terre ne crée pas les alizés, elle ne fait que dévier un vent déjà existant.
La plus belle manifestation de la force de Coriolis est assez tardive. Elle a lieu en 1851 lorsque Léon Foucault (1819-1868) met en oscillation sous la Coupole du Panthéon un pendule long de 67 mètres. Un phénomène déconcertant est observé : alors que rien ne perturbe le pendule, son plan d'oscillation pivote lentement autour de la verticale de son point d'attache. Au bout de 10 minutes, le plan a déjà tourné de deux degrés environ et il effectue un tour complet en un peu moins de 32 heures ! L'expérience est interprétée comme une nouvelle preuve de la rotation terrestre, la force de Coriolis perturbant l'oscillation du pendule. Si l'expérience avait lieu aux pôles, on verrait le plan d'oscillation du pendule parfaitement fixe par rapport aux étoiles et son pivotement en 23h56min ne serait que le reflet de la rotation de la Terre sous lui.
Aberration stellaire et parallaxe
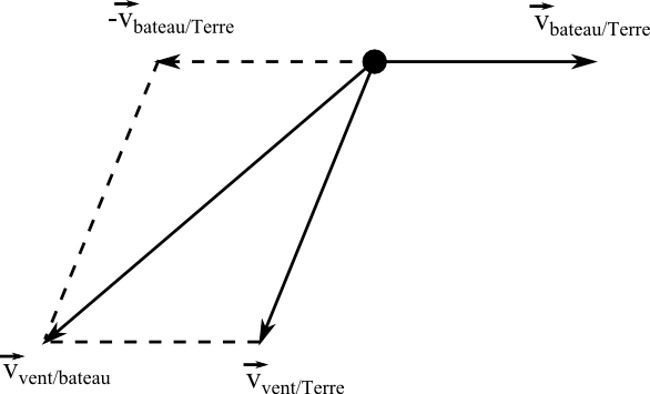
Pour apporter une preuve observationnelle à la révolution annuelle de la Terre autour du Soleil, les astronomes de la fin du XVIIe et du début du XVIIIe siècle sont toujours à la recherche d'une parallaxe stellaire. L'application des lunettes aux instruments astronomiques améliore considérablement la précision des mesures et laisse enfin espérer un résultat positif. Et pourtant, le mouvement parallactique des étoiles continue de se dérober aux astronomes mais, en le cherchant, ils mettent en évidence un autre phénomène inattendu : l'aberration des étoiles. En 1728, James Bradley (1693-1762) annonce qu'il a découvert une variation périodique annuelle dans la position des étoiles. Pour en comprendre l'origine, une analogie est utile. Supposons un voilier poussé par un vent uniforme. Bien que la direction du vent soit constante, la girouette du voilier s'oriente différemment en fonction du mouvement propre du bateau. Ainsi, le marin qui indiquerait la direction du vent à partir de l'orientation de la girouette sans tenir compte de son mouvement propre se tromperait, il serait victime d'une « aberration ». De la même manière, si la vitesse de la lumière est finie (à l'époque, il s'agit encore une hypothèse, malgré le travail remarquable d'Olaüs Roemer (1644-1710) en 1676 sur le retard des éclipses des satellites de Jupiter), alors la direction apparente d'une étoile résulte de la combinaison de deux vitesses, celle de la lumière provenant de l'étoile et celle de la Terre sur son orbite : il s'agit de l'aberration annuelle des étoiles. Puisque la vitesse orbitale de la Terre change au cours de l'année, la direction de l'étoile n'est jamais la même et varie annuellement. Les étoiles, observées depuis la Terre en mouvement, ne sont donc jamais vues dans leur position véritable, la déviation maximale étant de 20,5'' ! L'aberration est indépendante de la distance de l'astre et concerne l'ensemble des étoiles mais ces dernières ne sont pas affectées de la même manière en fonction de leur position par rapport à l'orbite de la Terre. L'aberration est la première manifestation observationnelle du mouvement de la Terre autour du Soleil.
Figure 16. Le principe de l'aberration
La direction du vent, observée depuis le bateau, est perturbée par le mouvement propre du bateau.
On a : .
Il faut attendre 1838 pour que la première parallaxe stellaire soit observée par Freidrich Wilhelm Bessel (1784-1846). Il observe qu'une étoile de la constellation du Cygne a une parallaxe de 0,314'' (la valeur moderne est de 0,292'') ! L'objection au mouvement de la Terre formulée dès qu'Aristarque avait proposé son hypothèse héliocentrique est enfin levée. La valeur trouvée indique que la distance de l'étoile est égale à 700 000 fois la distance moyenne du Soleil à la Terre, soit environ 1014 km. Copernic avait bien raison de vouloir reculer la sphère des étoiles mais il était loin de soupçonner que de telles distances seraient un jour découvertes.
Conclusion
Pendant la période qui s'étend de la publication Des révolutions des Orbes Célestes de Copernic en 1543 à la publication des Principes Mathématiques de la Philosophie Naturelle de Newton en 1687, la représentation du Monde a été entièrement bouleversée. Le Monde tel que le concevaient Aristote et ses partisans n'existe plus, un autre a pris la place ! Le bouleversement est multiple. Il concerne en premier lieu la place de la Terre dans l'espace avec le passage du géocentrisme à l'héliocentrisme : le Monde ne s'organise plus autour de la Terre mais autour du Soleil ; la Terre n'a pas une position privilégiée et ce sont ses mouvements qui expliquent le déplacement apparent des astres ! Il porte également sur la science du mouvement : les corps ne se mettent pas en mouvement pour être en accord avec leur nature profonde selon la théorie des lieux naturels mais parce qu'ils sont attirés par un autre corps selon la loi de la gravitation universelle ; leur mouvement est régi par la loi de l'impulsion qui postule que l'accélération est proportionnelle à la force agissante. Il concerne encore les méthodes scientifiques. Il y a, d'une part, une nouvelle manière de faire des sciences en manipulant, en opérant sur la nature. C'est l'expérience et non plus seulement la réflexion, qui ouvre à la compréhension du Monde. Il y a, d'autre part, un changement dans l'apport des mathématiques. La physique d'Aristote était une physique qualitative qui ne donnait pas prise aux mathématiques car les phénomènes qu'elle abordait étaient trop complexes et trop fugaces. Les mouvements célestes étaient bien analysés d'un point de vue mathématique mais dès que l'on s'intéressait au Monde réel, le modèle mathématique était transposé en un modèle physique avec des sphères matérielles qui tournaient uniformément en emportant les planètes. La situation change au XVIIe siècle : Galilée introduit les mathématiques dans la physique et donne les premières lois mathématiques de la chute des corps, Képler trouve empiriquement les lois mathématiques des mouvements célestes, et Newton découvre la loi mathématique de la gravitation qui se passe d'un intermédiaire physique. Il apparait l'idée étonnante que les mathématiques révèlent directement la structure du Monde. Cette nouvelle approche s'épanouit au XVIIIe siècle grâce au développement de l'outil mathématique et la mise au point du calcul différentiel et intégral. Le passage du géocentrisme à l'héliocentrisme est donc bien plus qu'un simple changement de point de vue. On peut remarquer que cette "marginalisation" de la Terre s'est poursuivie. Après que la Terre a été remplacée par le Soleil comme centre de l'Univers, le Soleil a lui-même été relégué au rang de banale étoile bien loin du centre de notre galaxie, elle-même dans une position quelconque de l'univers observable. Après Newton, le Monde n'est pas seulement regardé depuis le Soleil plutôt que depuis la Terre mais ce sont la conception globale que l'homme se fait du Monde et la manière de se faire cette conception qui sont complètement chamboulées.
Articles de la série « La structure du Monde » :
Bibliographie citée et complémentaire
G. Bruno, 1987. L'infini, l'univers et les mondes, trad. B. Levergeois, Paris, Berg International, 176p.
M. Clavelin, 1996. La philosophie naturelle de Galilée, Paris, Albin Michel, 512p.
J. Gapaillard, 1993. Et pourtant, elle tourne !, Paris, Seuil, 347p.
A. Koyré, 1961. La révolution astronomique, Paris, Hermann, 525p.
A. Koyré, 1968. Études Newtoniennes, Paris, Gallimard, 353p.
J.-P. Verdet, 1993. Astronomie et Astrophysique, Paris, Larousse, 830p.
A.D. Wittman, Z.T. Xu, 1987. A catalog of sunspot observations from 165 BC to AD 1684, Astron. Astrophys. Suppl. Ser, 70, 83-94 [pdf]
Pour citer cet article :
La structure du Monde - La nouvelle astronomie (3/3), Deparis, juin 2017. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/nouvelle-astronomie.xml