Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Les marées depuis Newton
17/09/2018
Résumé
Remonter dans le temps, le long des lignes cotidales, et parler de quelques hommes à qui sont attribués des résultats importants concernant l'aspect dynamique des marées.
Table des matières
Transcription par Yves Gomas de la présentation de Frédéric Chambat du 04 janvier 2016 à l'ENS de Lyon, donnée dans le cadre du cours pluridisciplinaire des écoles doctorales EPIC, PHAST et INFOMATH intitulé La Terre, sa forme, sa rotation, ses marées - Morceaux choisis mathématiques, géophysiques et historiques.
1. L'histoire comme continuum
L'attention se focalise facilement sur quelques personnages clés comme Harris, Whewell, Laplace, Lagrange, d'Alembert. L'histoire retient certaines choses et attribue des résultats marquants à quelques hommes. Mais ceux-ci se sont appuyés sur d'autres, et il est souvent possible de trouver des traces de leurs idées novatrices dans des travaux antérieurs.
Sous certains aspects, l'évolution des connaissances peut être considérée comme un continuum. D'autre part, les études d'histoire des sciences sont elles-mêmes « en mouvement » et de nouvelles études font souvent apparaitre des éléments négligés auparavant.
2. Quelques « grands noms »
2.1 Rollin Arthur Harris (1863-1918)
Ce mathématicien et océanographe américain semble être le premier à avoir représenté les points amphidromiques[1] et l'importance des résonances dans les bassins fermés. Il a fait des expériences sur des modèles réduits.
Certes, les résultats obtenus par Laplace contiennent implicitement la possibilité de résonances, par la présence de termes en (ω2 - Ω2). Mais il y a une différence importante entre la possibilité implicite d'obtenir un résultat, et le fait d'énoncer celui-ci de façon explicite !
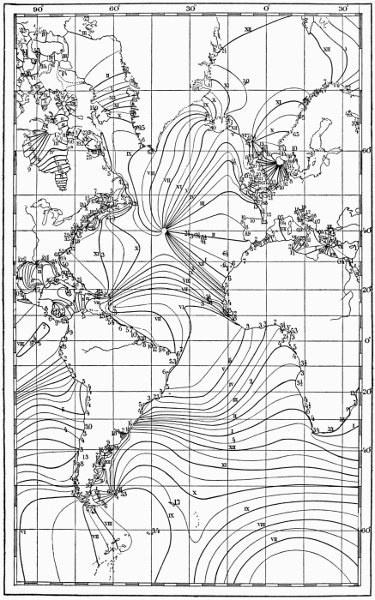
Source - © 1909 in R.A. Harris, The tides: Their causes an representation (Popular Science Monthly, Vol. 74)
Figure 1. Carte de R.A. Harris avec points amphidromiques
Les lignes sont des lignes cotidales (points de même phase de marée, voir ci-dessous). Les chiffres romains sont placés du côté des lignes cotidales vers lequel l'onde de marée semble progresser. Les chiffres arabes sur les côtes donne l'amplitude de marée moyenne observée (en pieds).
Un point d'amplitude de marée nulle en mer est mis en évidence dans l'Atlantique vers 40° de latitude Nord et 40° de longitude Ouest. Un autre est visible dans le bassin de Foxe (au Nord de la baie d'Hudson) ainsi qu'un autre près de la côte Sud de l'Argentine. Les autres cartes de la publication montrent un point amphidromique dans l'Océan indien (à mi-chemin entre Madagascar et la péninsule indienne), un entre Malaisie et Indonésie, un entre actuelle Corée du Sud et Japon et quatre dans le Pacifique.
2.2 William Whewell (1794-1866)
Whewell était un polymathe, c'est-à-dire qu'il possédait des connaissances approfondies dans de nombreux domaines. Il a publié des travaux en physique, en astronomie, en économie, en histoire des sciences ; il a été professeur de minéralogie et de philosophie, et directeur du Trinity College à Cambridge ; il s'est intéressé à la théologie morale ; il a écrit des poèmes, traduit Goethe, suggéré de nouveaux mots à Faraday au sujet de ses découvertes en électricité… Bref, un personnage étonnant !
C'est à lui que l'on doit les premières cartes des lignes cotidales[2], et l'invention du mot lui-même. Ses cartes de 1833 ne montrent pas de points amphidromiques[1]. Il ne disposait que des données relevées sur les côtes, et ne pouvait pas tracer complètement les lignes qui sont seulement amorcées. Sa carte de l'Atlantique est nettement différente de celles dont nous disposons actuellement, mais fait bien apparaitre qualitativement le décalage progressif en fonction de la latitude.
Source - © 1833 in W. Whewell, Essay towards a first approximation to a map of cotidal lines (Philosophical Transactions of the Royal Society of London, 123, 147-236)
Figure 2. Lignes cotidales sur une carte W. Whewell
Carte reprise dans un article récent de Steffen Ducheyne (2010), Whewell’s tidal researches: scientific practice and philosophical methodology (Studies in History and Philosophy of Science ,Part A, Vol. 41, 1, 26-40)
2.3 Joseph-Louis Lagrange (1736-1813) et Pierre-Simon Laplace (1749-1827)
Ces deux noms sont liés à la théorie des marées. Lagrange a établi les principes de la propagation des ondes en eaux peu profondes.
Laplace a publié une longue série de travaux sur les marées : expression du mouvement en coordonnées sphériques, tenant compte de la rotation de la Terre bien avant Coriolis, expression du potentiel de marée, invention des harmoniques sphériques, solution générale pour une planète sans continents, étude de la réponse dynamique des océans… Il a aussi organisé les observations et mis au point les méthodes pour les analyser. Pour cela, il effectue une décomposition en 9 ondes dont il ajuste l'amplitude et la phase.
Dans son ouvrage Mécanique Céleste (1825), Laplace affirme : « Le mouvement des fluides qui recouvrent les planètes était donc un sujet presque entièrement neuf, lorsque j'entrepris, en 1774, de le traiter ».
Lagrange, dans son Mémoire sur la théorie du mouvement des fluides (1781), montre l'analogie entre les ondes à la surface de l'eau et celles formées « par les condensations et raréfactions successives de l'air », ce qui permet de les traiter par les mêmes méthodes. Et il écrit qu'il s'agit d'une « analogie que plusieurs auteurs avaient déjà supposée, mais que personne jusqu'ici n'avait encore rigoureusement démontrée ».
Ces affirmations de Laplace et de Lagrange peuvent nous surprendre, puisque d'Alembert avait déjà travaillé sur ces questions bien avant eux.
Jean Le Rond d'Alembert (1717-1783)
Dans ses Réflexions sur la cause générale des vents de 1747, d'Alembert traite en grande partie des marées, puisqu'il étudie de façon générale la réponse d'un fluide à une attraction. Il montre que cette réponse ne dépend pas seulement de l'attraction, et, sans utiliser le mot, il envisage une sorte de bassin, formé de montagnes très hautes encadrant une portion d'atmosphère. Il montre aussi pourquoi, lorsque la vitesse de l'onde est inférieure à la vitesse apparente de l'astre attracteur pour un observateur au sol, « le fluide doit s'abbaisser au-dessous de l'astre, lorsqu'au contraire il sembleroit devoir s'élever ».
Source - © 1747 d'Alembert
Bon nombre d'autres notions semblent déjà présentes dans cet ouvrage, en particulier l'aspect dynamique des marées et le fait que l'onde se propage en (g.h)1/2. D'autre part, d'Alembert a étudié l'écoulement d'un fluide dans un canal de largeur variable. À partir de la question « le niveau de l'eau va-t-il s'élever ou s'abaisser en cas de rétrécissement », il obtient des solutions qui correspondent à ce que nous appelons maintenant le régime fluvial et le régime torrentiel.
D'Alembert a très probablement réagi aux affirmations de Laplace et Lagrange, qui ont été obligés de lui rendre hommage pour ses idées au sujet des marées. Précisons que Laplace était un protégé de d'Alembert, à qui il devait son premier poste de professeur. Quant à Lagrange, d'Alembert l'avait recommandé pour un poste à l'académie de Berlin. Les trois hommes échangeaient de nombreuses lettres, voici quelques passages de cette correspondance pour éclairer les questions de priorité.
Sur le point de remettre un mémoire sur les marées à l'Académie, Laplace écrit à d'Alembert le 15 novembre 1777. Il lui assure qu'il a bien inclus un additif précisant que « c'est donc à proprement parler à M. Dalembert qu'il faut rapporter les 1ères recherches exactes qui ayent paru sur cet important objet. Cet illustre autheur s'étant proposé dans son excellent ouvrage qui a pour titre : Réflexions sur la cause des vents, de calculer les effets de l'action du soleil et de la lune sur notre atmosphère […] parvient par une analyse aussi sçavante qu'ingénieuse aux véritables équations de ce problème […] ».
Quelques mois plus tard, le 10 juillet 1778, Lagrange écrit à son tour à d'Alembert : « J'ai relu, ces jours passés, à l'occasion du mémoire de M. de la Place sur le flux et le reflux de la mer, votre Ouvrage sur la cause des vents […] que j'avais toujours regardé comme le premier de tous vos Ouvrages, par la beauté, la nouveauté et la multiplicité des méthodes qu'il renferme. […] Les nouveaux pas que M. de la Place a faits dans la théorie du flux et du reflux sont dignes de lui et du rang qu'il tient du premier de vos élèves en France ».
Isaac Newton (1643-1727)
À la source de l'étude mathématique des marées, nous trouvons évidemment les Principia de Newton. La proposition 65 du Livre I concerne le problème du mouvement à n corps. La proposition 66 et les 22 corollaires généraux qui suivent restreignent le problème à 3 corps. Newton prévoit, dans ce cas, des trajectoires qui sont des ellipses perturbées et il en évalue les perturbations.
Source - © 1759 Trad. de Newton par Mme la Marquise du Châtelet
Figure 4. Les "Principes mathématiques de la philosophie naturelle" de Newton (1759, traduction française)
Lien vers la ressource Gallica des Principes mathématiques de la philosophie naturelle..., par Isaac Newton 1759
Dans le Livre III, une série de propositions reprend ces corollaires en les appliquant au mouvement de la Lune et aux marées. Pour évaluer les perturbations de la trajectoire lunaire, il utilise une méthode géométrique en décomposant la force exercée par le Soleil en trois autres forces. Pour les marées, il applique une méthode comparable en imaginant un canal entourant la Terre, et il tient compte de l'aplatissement tel qu'il l'a évalué.
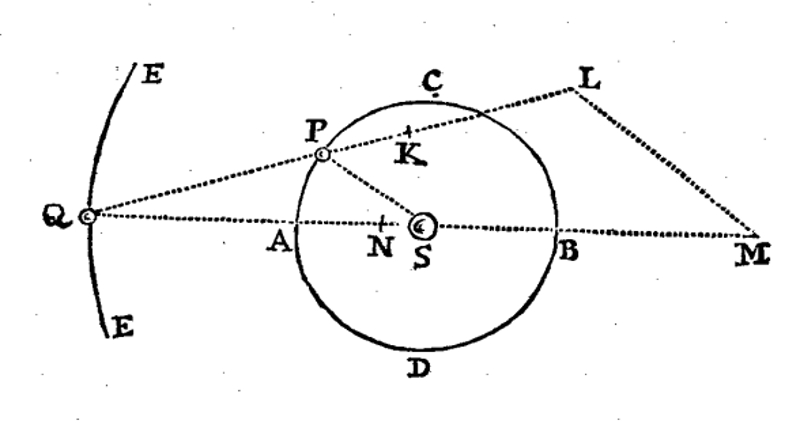
Source - © 1687 I. Newton, in Philosophiae naturalis principia mathematica, édition originale en latin
Figure 5. Illustration d'un problème à trois corps, dont deux (Q et P) tournent autour du troisième (S)
Cette figure sert à illustrer, entre autres, les questions de quadrature, conjonction et opposition des planètes autour du Soleil.
En plus des considérations théoriques, les propositions du Livre III utilisent les observations faites dans les ports et sur les côtes pour en déduire des paramètres astronomiques. Les résultats de Newton sont nettement différents de ceux déterminés par la suite, mais l'ordre de grandeur est à peu près correct. Par exemple, les marées mesurées dans le canal de Bristol le conduisent à un rapport des effets de la Lune et du Soleil L/S = 4,48, alors que la valeur exacte est proche de 2,2. Pour le rapport des masses de la Terre et de la Lune, il trouve 39,8 alors que Bernouilli trouve 70 et d'Alembert 78, la valeur exacte étant proche de 81.
3. Pistes d'exploitation
4. Les autres articles du dossier La Terre, sa forme, sa taille, sa rotation :
- La Terre est ronde ! Ératosthène et la mesure du rayon terrestre
- Les mesures de méridien vont-elles confirmer la théorie de Newton ?
- La Terre ellipsoïde ? Les mesures de la gravité au XVIIIe siècle
- Clairaut et sa bande, l'expédition de Clairaut et Maupertuis en Laponie
- La Terre tourne... Le gyroscope de Foucault
- Les machines de lord Kelvin
Bibliographie
R.A. Harris, 1909. The Tides: Their Causes And Representation, The Popular Science Monthly
William Whewell, 1833. Essay toward a first approximation to a map of cotidal lines, Philosophical Transactions, 147-236
William Whewell, 1834. On the empirica1 1aws of the tides in the Port of London, with some reflections on the theory, Philosophical Transactions, 15-45
Pierre-Simon Laplace. 1778-1820. Quatre mémoires de l'Académie royale des sciences : deux Recherches sur plusieurs points du système du Monde 1775 (1778), 1776 (1779) et deux autres Sur le flux et le reflux de la mer 1790 (1797), 1818 (1820). Rééd. Traité de mécanique céleste, livre IV, tome II (1799) et livre XIII, tome V (1825)
Joseph-Louis Lagrange, 1781. Mémoire sur la Théorie du Mouvement des Fluides, Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Berlin. Rééd. Œuvres de Lagrange, Gauthier-Villars, Paris, France, 1867, J.A. Serret Ed., T. 4, 695-748
Pour citer cet article :
Les marées depuis Newton, Chambat, Gomas, septembre 2018. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/marees-depuis-Newton.xml