Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Les bulles s'attirent-elles ?
10/10/2005
Résumé
Pourquoi les bulles tendent-elles à se regrouper au bord d'un récipient ? Pourquoi les corps flottant dans un récipient ont tendance à se rapprocher et à se coller ensemble et aux bords du récipient qui les contient ?
Table des matières
Pourquoi les bulles tendent-elles à se regrouper au bord d'un récipient ? Pourquoi les corps flottant dans un récipient ont tendance à se rapprocher et à se coller ensemble et aux bords du récipient qui les contient ?
Vous savez certainement que les bulles dans un récipient ont tendance à se regrouper ensemble, et à se rapprocher des bords.

Les bulles sont toutes réunies ensemble sur les bords du récipient... Pourquoi ?
Figure 1.
Il en est de même avec de nombreux objets : par exemple, les céréales soufflées dans le lait semblent s'attirer elles aussi...
Ici, on a filmé l'évolution de petites billes de polystyrène dans un récipient rempli d'eau :

En cliquant ici, vous pouvez voir les petites billes de polystyrène se rapprocher les unes des autres ainsi que du bord du récipient
Figure 2.
D'où vient donc ce phénomène ?
La réponse :
Pour répondre à ces questions, observons de plus près l'image précédente...

Vue de près du récipient dans lequel on a fait l'expérience
Figure 3.
On remarque, en regardant l'image de près, la présence d'un ménisque au bord du récipient. Ce ménisque est un effet bien connu des forces de tension superficielle.
En fait, on va voir que les effets de tension superficielle peuvent aussi exercer une force sur les objets flottants dans un récipient... et causer le déplacement que nous avons constaté.
Rappels sur la tension superficielle (aussi appelée "tension de surface")
L'énergie associée à la surface libre S d'un matériau (solide, liquide ou gazeux) est :
E = γ S
où γ est la tension superficielle de ce matérieu. γ s'exprime en J.s-2 ou en N.m-1 Pour un liquide, à volume constant, la minimum de l'énergie s'obtient pour une surface sphérique. Ceci explique la forme sphérique des gouttes de pluie, celle que prennent spontanément les liquides en apesanteur, dans une navette spatiale par exemple, ainsi que cette des bulles de savon*.
Dans le cas des bulles de savon, cependant, on ne raisonne pas vraiment "à volume constant", puisque le gaz emprisonné dans la bulle est compressible -alors que les liquides ne le sont quasiment pas- : on montre que l'équilibre est atteint pour des pressions intérieures et extérieures à la bulle différentes : l'intérieur de la bulle est alors en légère surpression par rapport à l'extérieur.

La forme sphérique des gouttes d'eau permet de minimiser l'énergie de surface
Figure 4.
Energie et tension interfaciales
Dans la vie courante, cependant, on a, pour l'essentiel, des interfaces entre deux milieux plutôt que des surfaces libres (en toute rigueur, dans les cas précédents, on parlait déjà d'interface entre un liquide et l'air). Ces milieux peuvent être solides, liquides ou gazeux, et de natures variées.
L'énergie associée à une interface entre deux milieux 1 et 2, de surface S, vaut :
E = γ12 S
où γ12 est la tension interfaciale, exprimée, comme tout à l'heure, en J.s-2 ou N.m-1.
Mouillage d'une surface, capillarité...
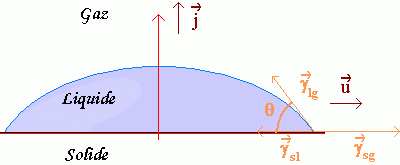
Goutte de liquide déposée à la surface d'un solide
Figure 5.
De la valeur de l'énergie de surface, on peut déduire la force par unité de longueur s'exerçant à l'interface entre les trois milieux : solide, liquide et gazeux. Cette force est la somme de trois forces, une pour chaque interface. À l'interface liquide-solide est associée la force par unité de longueur γsl, à l'interface solide-gaz on associe γsg et à l'interface liquide gaz γlg.
La norme de ces forces par unité de surface est égale à la tension interfaciale correspondant à chacun des interfaces, la force est dans le plan de l'interface, perpendiculaire à la ligne de contact entre les trois phases, et elle est dirigée vers l'intérieur de l'interface, come indiqué sur le schéma.
On a donc :
Ftotale par unité de longueur = γsl + γsg + γlg
Soit, projeté sur le vecteur i,
Force suivant i = - γsl + γsg - γlg cos θ
Lorsque l'équilibre est atteint, la force interfaciale suivant i est nulle.
On en déduit l'équation (équation dite "de Young") suivante :
cos θ = (γsg - γsl)/γlg
en fait, on ne s'est pas intéressé à la force suivant j. On voit bien qu'elle n'est pas nulle, sauf pour θ = 0 ou π. Cette question est traitée de façon plus détaillée ici.
On peut appliquer cette équation au cas d'une goutte d'eau posée sur du Téflon, par exemple, connaissant
- γeau-air = 0,072 J.m-2
- γeau-téflon = 0,050 J.m-2
- γair-téflon = 0,019 J.m-2
On trouve θ = 115,5°. On voit donc que θ > 90°, ce qui se traduit par un schéma différent de celui représenté plus haut :

Une goutte d'eau posée sur du téflon
Figure 6.
Dans le plus grand nombre de cas : cas d'une goutte d'eau posée sur du verre, par exemple, cependant, on a γsg > γsl et θ < 90°.
Le point de vue énergétique et le point de vue en terme de forces sont, bien entendu, équivalents. On peut démontrer d'autres relations sur le mouillage des surfaces, en utilisant le point de vue énergétique. Citons-en quelques-uns pour mémoire :
- Par exemple, en minimisant l'énergie totale d'une goutte (énergie de surface et énergie potentielle de pesanteur) supposée presque plane à son sommet, on montre que la hauteur de la goutte est : z = (2 γliquide-air (1 - cos θ)/(ς g))1/2 où θ est l'angle au bord de la goutte, calculé précédemment, et ς est la masse volumique du liquide.
- On montre aussi que la surpression existant au point M à l'intérieur d'un liquide en contact avec l'air est γliquide-air C où C est la courbure totale de l'interface en M (C = 1/R + 1/R' si R et R' sont les deux rayons de courbure principaux de la surface au point M : R = R' = rayon de la sphère dans le cas d'une sphère, R et R' sont infinis dans le cas d'un plan, et, dans le cas d'un cylindre de rayon r, R est infini et R' = r).
- On peut montrer enfin que le liquide a tendance à monter dans un tube de rayon r d'une altitude z = 2 γliquide-air cos θ /(ς g r). Il convient ici de bien noter que θ est, là encore, l'angle calculé dans la démonstration que l'on a détaillée plus haut. Pour le calcul, on cherche à minimiser la somme de l'énergie de surface et de l'énergie potentielle de pesanteur : il y a compétition entre la montée du liquide dans le tube, favorisée par les effets de tension superficielle, et sa redescente favorisée par la pensateur.
Application au cas de corps flottant dans un liquide
Le cas d'un corps flottant dans un liquide est similaire aux précédents : la différence principale est que, cette fois, le corps flottant peut se déplacer afin de minimiser l'énergie du liquide.
Se rapprocher du bord, à hauteur de liquide le long des parois solides égale, permet de "réunir" les deux ménisques et ainsi de minimiser la superficie de l'interface liquide-air.
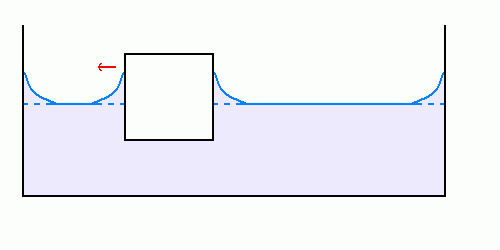
Le corps flottant est loin du bord, il se déplace à très faible vitesse en direction du bord le plus proche, de façon quasi-imperceptible
Figure 7.
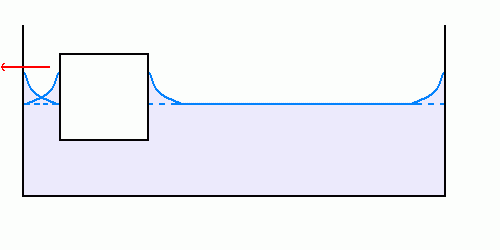
Dès que le corps flottant est plus proche du bord, sa vitesse s'accroît fortement
Figure 8.
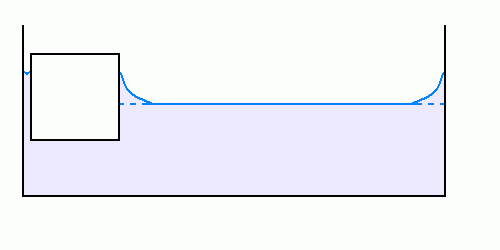
Finalement, le corps flottant vient se coller contre le bord, ne laissant qu'une très fine couche de liquide entre lui et le bord
Figure 9.
Via un comportement semblable, on voit peu à peu tous les corps flottants se rapprocher les uns des autres et venir se coller aux bords les plus proches.

Un bouchon flottant dans du lait est venu se coller à la paroi du récipient
Figure 10.
Sur les trois schémas ci-dessus, on voit que le mouvement du corps flottant vers le bord permet de diminuer la superficie de l'interface eau-air, les surfaces des autres interfaces restant constantes : ceci est donc énergétiquement favorable.
La variation de surface de l'interface lorsque le corps flottant se déplace est faible tant que ce-dernier est loin du bord du récipient, elle devient beaucoup plus importante dès qu'il se rapproche du bord : ceci explique la vitesse de mouvement du corps flottant, d'abord très faible, mais qui s'accélère dès qu'il se rapproche des parois.
En fait, comme on peut le constater sur la photo du bouchon flottant dans du lait, la hauteur de la fine couche de liquide entre le bouchon et la paroi du récipient est supérieure à celle du ménisque de départ : ce phénomène est normal et analogue au phénomène bien connu de montée du liquide par capillarité entre des parois solides très proches.
Attention !
Le comportement décrit ici peut être inversé : nous avons vu que, dans le cas d'une goutte d'eau posée sur du téflon, par exemple, l'angle θ est supérieur à 90°. De fait, la plupart des comportements que nous avons décrits dans le cas le plus général (eau sur verre, etc.) sont "inversés" : un capillaire de téflon plongé dans de l'eau verra le niveau de l'eau dans le capillaire être inférieur à celui de l'eau dans le récipient... Le ménisque au bord d'un récipient en téflon contenant de l'eau est lui aussi incurvé vers le bas...
D'une façon générale, si joindre deux ménisques incurvés vers le haut est énergétiquement favorable, joindre un ménisque incurvé vers le bas avec un ménisque incurvé vers le haut, au contraire, coûte de l'énergie...
Pour citer cet article :
Les bulles s'attirent-elles ?, Gabrielle Bonnet, octobre 2005. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/QSattirance.xml




