Activer le mode zen
Ressource au format PDF
Classification
Entraînez votre première IA en python - Tuto interactif de reconnaissance de chiffres manuscrits avec la librairie scikit-learn, aucune installation nécessaire
L'intelligence artificielle : introduction et applications en physique (2/3)
28/06/2021
Résumé
Vous êtes-vous déjà demandé s'il était possible de créer sa propre IA ? Et de l'utiliser dans ses recherches en physique ou dans l'industrie ? C'est ce que nous allons voir dans cette série de 3 articles : L'intelligence artificielle : introduction et applications en physique.
Dans ce deuxième article nous proposons un tutoriel pour prendre en main l'intelligence artificielle et l'entraîner à reconnaître des chiffres manuscrits.
Colin Bernet est chargé de recherche au CNRS, créateur du blog https://thedatafrog.com, et cofondateur de https://cynapps.ai.
Série de 3 articles : L'intelligence artificielle : introduction et applications en physique
Article précédent 1/3 : « L'intelligence artificielle, c'est quoi ? - Une explication pour les physiciens ».
1. Un exemple simple de classification d’images en python
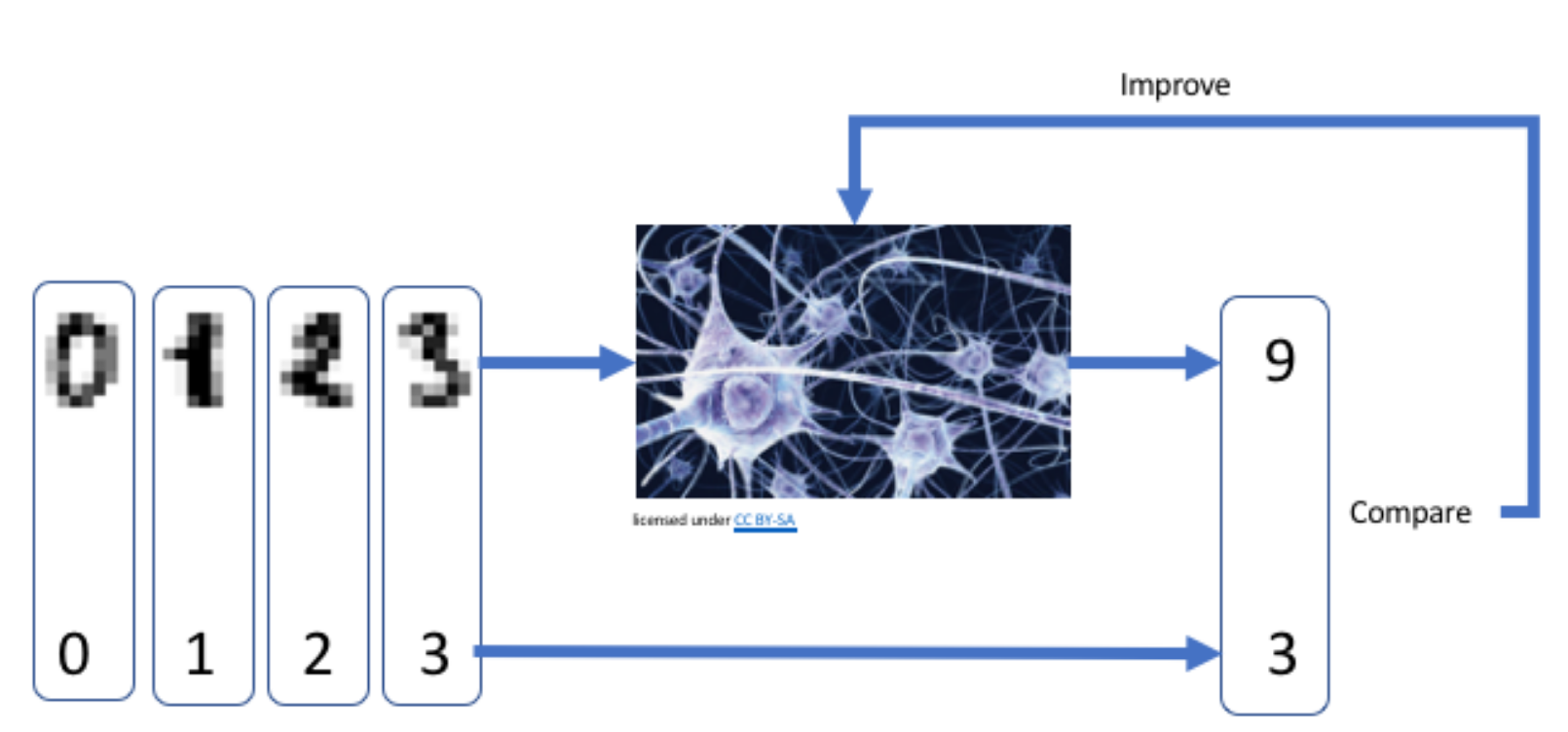
De manière générale, un modèle de classification d’images fonctionne comme présenté sur la figure 1 :
L'utilisateur fournit au modèle un échantillon d’images étiquetées par un humain, ici des chiffres manuscrits.
Chaque image est constituée de pixels, avec dans chaque pixel un niveau de gris, ou trois niveaux de couleurs. Ci-dessus, nos images sont en noir et blanc, et font 8x8 pixels. Chaque image est donc représentée par 64 valeurs. Ces images sont des points dans un espace à 64 dimensions.
Le modèle est une fonction de ces 64 valeurs, qui fournit une unique valeur en sortie, sa prédiction pour le chiffre représenté par l’image.
Ici, on fournit d’abord une image du chiffre 3 au modèle. Le modèle prédit que cette image correspond au chiffre 9, et donc se trompe. Le programme compare cette prédiction à l’étiquette correspondante (3), et quantifie l’erreur commise par le modèle. À partir de cette erreur, le programme adapte l’ensemble des paramètres du modèle pour se rapprocher de la prédiction désirée. Puis il passe aux images suivantes. À la longue, le modèle devient capable de reconnaître de nouveaux chiffres avec précision.
2. Tutoriel en python
Nous proposons un petit tutoriel dans lequel vous pourrez entraîner vous-même un réseau de neurones à reconnaître des chiffres manuscrits. Le tutoriel est sous Jupiter :
https://colab.research.google.com/drive/111UBhv3yeeCp2QUO5Hln4O4y6AygRQrK?usp=sharing
Sur cette page, exécutez les cellules de code dans l’ordre en pressant shift+entrée.
Les programmes sont aussi disponible en téléchargement en fin d'article (format .py et .ipynb).
Dans un premier temps afin de se familiariser avec la procédure, nous proposons ici d'en décrire les différentes étapes.
- Tout d'abord on importe le set d'images de chiffres que l'on stocke dans digits.
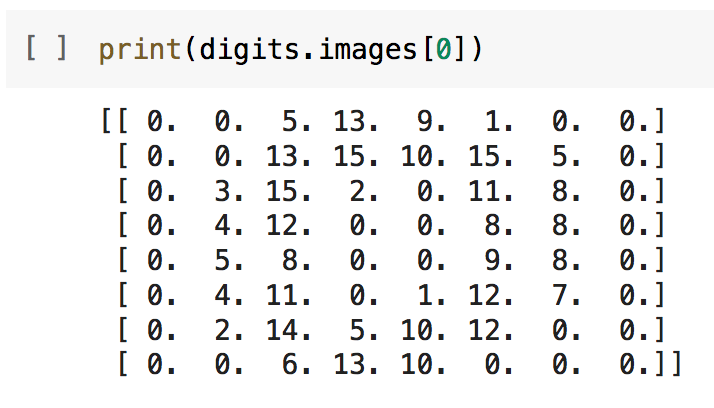
- On affiche la première image. Attention ici digits.images[0] indique que l'on prend le premier élément de la matrice digits.images, il se trouve qu'ici le premier élément est un '0'.
À l'aide de la fonction print, on affiche une matrice donnant les valeurs de niveaux de l'image du chiffre en 8x8 pixels (à gauche). À l'aide de matplotlib, on affiche sa représentation graphique (à droite).
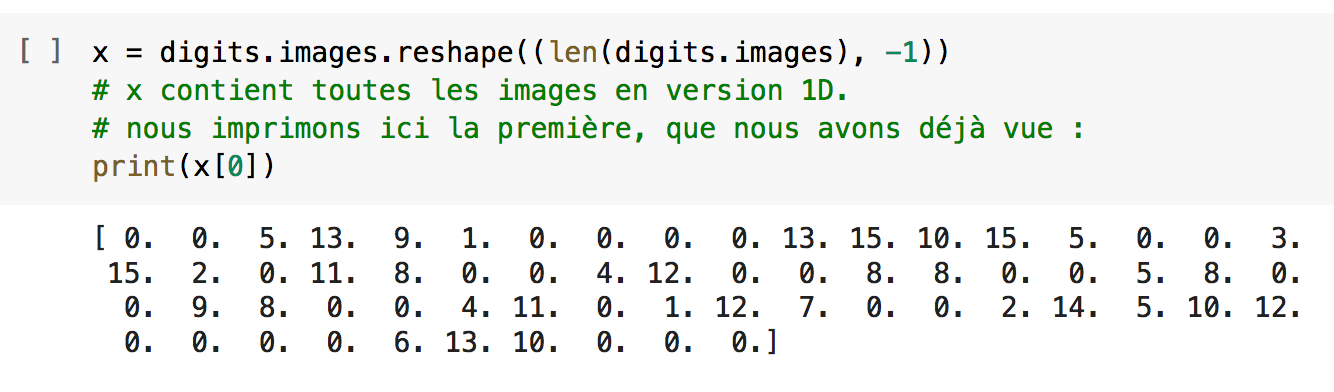
- Nous souhaitons entraîner un réseau de neurones simple à reconnaître les chiffres dans ces images. Ce réseau va prendre en entrée des tableaux 1D de 8x8=64 valeurs. Nous devons donc convertir nos images 2D en tableaux 1D.
La matrice x comprend maintenant les échantillons des chiffres sous forme de vecteurs de 64 valeurs. Ici, on affiche le vecteur correspondant au premier chiffre du set d'échantillon, le '0'.
Le réseau va agir comme une fonction permettant de passer d'un tableau de 64 valeurs en entrée à une valeur en sortie qui est son estimation du chiffre. Les valeurs de sortie sont sockées dans la variable y, cela correspond à "la cible".
- Nous décidons de créer un réseau de neurones relativement simple utilisant 15 neurones. Avec le langage python et ses librairies de machine learning, il est aujourd'hui simple et rapide d'entraîner ses propres réseaux de neurones. Par exemple, scikit-learn[1] fournit des outils de machine learning de haut niveau avec simplement deux lignes de code :
Nous allons entraîner ce réseau sur les 1000 premières images de notre set d'échantillons, et réserver les images suivantes pour tester les performances du réseau.
On définit x_train comme les 1000 premiers vecteurs de x (donc correspondant aux 1000 premières images), et x_test comme les vecteurs de x mais à partir du millième élément, pour réaliser les tests.
De la même manière y_train et y_test comme les vecteurs de x mais à partir du millième élément, pour réaliser les tests.
L'entraînement se fait en une ligne de code : mlp.fit(x_train, y_train)
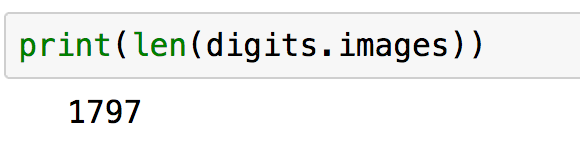
Il est possible de connaître le nombre total d'échantillon de la banque de données à l'aide de la fonction len (pour lenght). ici 1780 images sont disponibles.
- Nous pouvons maintenant regarder ce que donne le réseau pour les images suivantes, qui n'ont pas été vues par le réseau lors de l'entraînement. Nous réalisons le test pour les 10 premières images de test (x_test [:10]) et nous comparons les résultats avec la cible (y_test [:10]).
Pour les 10 premières images de test, les estimations sont excellentes !
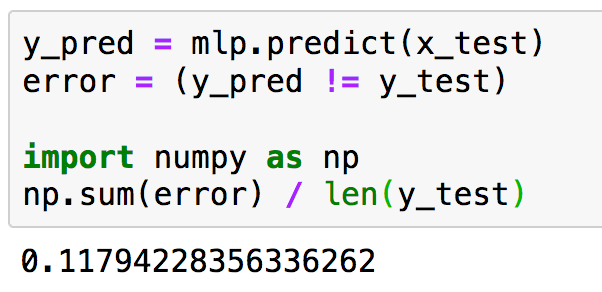
- Nous pouvons maintenant évaluer le réseau pour toutes les images de test.
Le vecteur y_pred contient l'ensemble des prédictions sur les images de test. On clacul le nombre d'images avec erreur en comparant les valeurs estimées (y_pred) avec les cibles (y_test). L'opérateur qui permet de comparer deux éléments différents s'ecrit '!=' en python.
Le taux d'erreur s'écrit comme la somme du nombre d'images pour lesquelles il y a une erreur de prédiction, divisée par le nombre total d'images testées.
Dans l'exemple présenté ici, on a un taux d'erreur d'environ 11,8%, ce qui signifie que 88,2% des prédictions sont correctes.
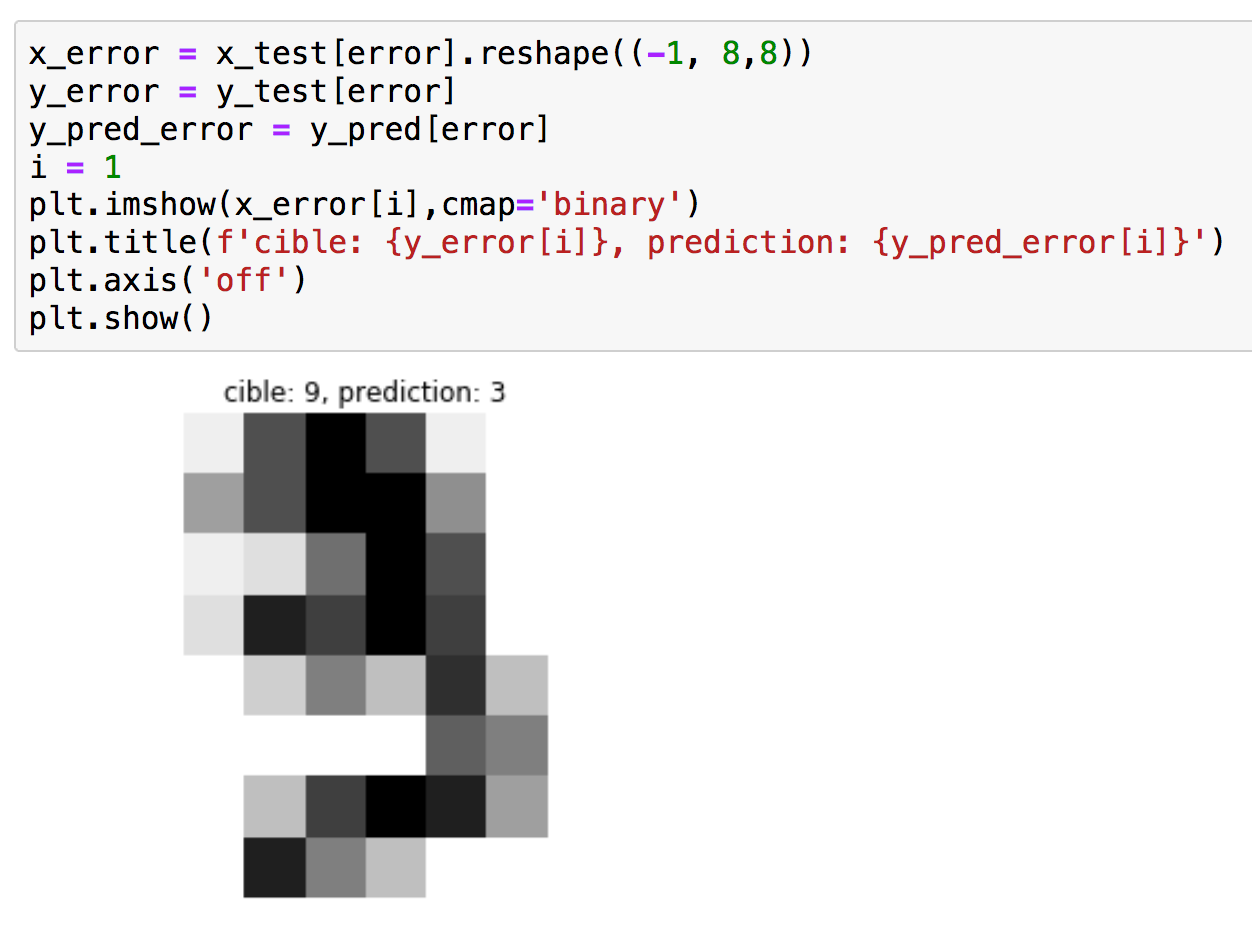
Nous pouvons enfin sélectionner les mauvaises prédictions pour les afficher. Ici nous choisissons le 2ème élément dont la prédiction est érronée (i=1, attention on commence à compter à partir de 0).
Il est aussi possible d'utiliser notre réseau pour reconnaître de nouveaux chiffres manuscrits.
Dans cet exercice, nous avons utilisé un réseau de neurones extrêmement simple et classifié des images de basse résolution.
Programmes python :
Télécharger le programme python au format Jupyter Notebook : Reconnaissance-chiffres-IA-Colin-Bernet.ipynb
Télécharger le programme python : Reconnaissance-chiffres-IA-Colin-Bernet.py
Nous allons maintenant voir dans l'article suivant comment le deep learning a permis de révolutionner la classification d’images.
Série de 3 articles : L'intelligence artificielle : introduction et applications en physique
Article 1/3 :« L'intelligence artificielle, c'est quoi ? - Une explication pour les physiciens ».
Pour citer cet article :
Entraînez votre première IA en python - Tuto interactif de reconnaissance de chiffres manuscrits avec la librairie scikit-learn, aucune installation nécessaire., Colin Bernet, juin 2021. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/IA-Bernet-2.xml