Activer le mode zen
Ressource au format PDF
Classification
Mesure de la vitesse de la lumière par l'expérience historique de Foucault
30/04/2019
Travail réalisé dans le cadre des XXVIe Olympiades de Physique sous la tutelle de Jean-Pierre Pichoud, professeur de Physique-Chimie.
Résumé
Plus connu pour ses travaux sur la mise en évidence de la rotation de la terre avec la célèbre expérience du pendule de Foucault, ce physicien de génie fût le premier à mesurer la vitesse de la lumière dans un laboratoire. Il n’en fallu pas moins pour éveiller notre curiosité et nous lancer dans cette grande aventure de la mesure de la vitesse de la lumière dans notre laboratoire du club de sciences.
Table des matières
introduction
Nous sommes quatre élèves du club de sciences du lycée Yves Leborgne en Guadeloupe. Nous avons souhaité, sur la proposition de notre camarade Luciani Mery, reproduire l'expérience historique de la mesure de la vitesse de la lumière mise au point par Léon Foucault en 1850. Nous nous sommes imposés comme contraintes de reconstituer au plus près le montage expérimental historique à l'aide du matériel optique du lycée et de réaliser la mesure dans la salle mise à notre disposition pour le club science.
1. Principe de la méthode du miroir tournant
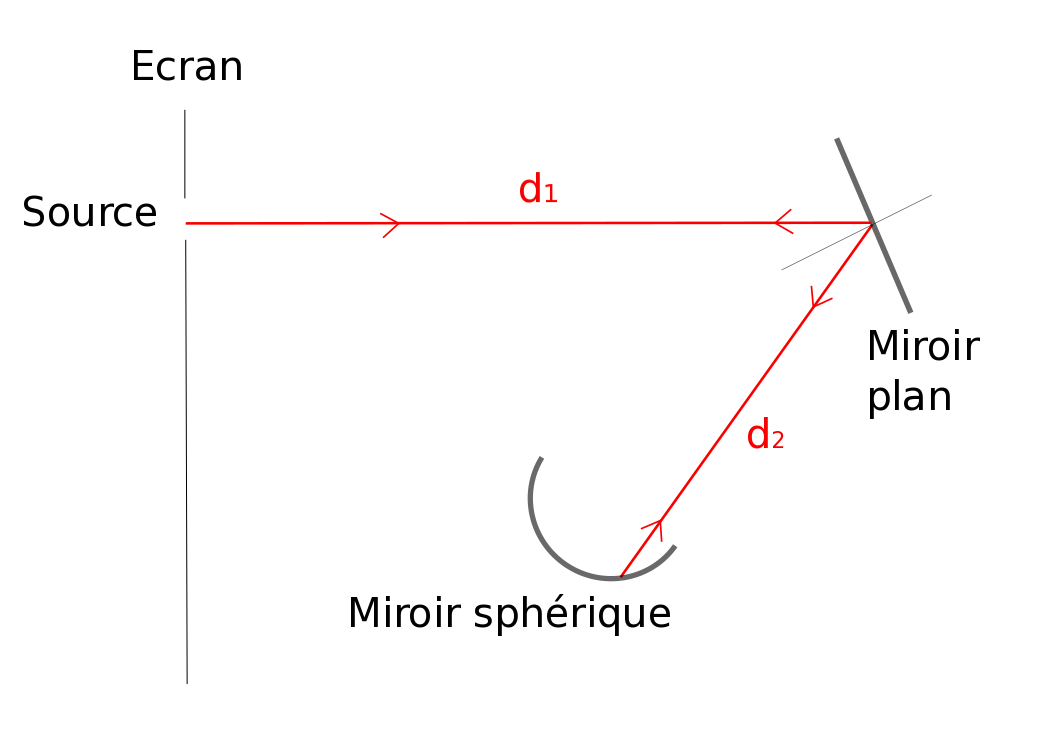
Léon Foucault détermina la vitesse de la lumière à Paris en 1862[1]. L’idée de Léon Foucault consistait à éclairer avec une source lumineuse un miroir plan placé au centre de courbure d’un miroir sphérique, figure 1. Le miroir plan est orienté de manière à ce que la lumière se réfléchisse sur le miroir sphérique. Les rayons qui se réfléchissent sur le miroir sphérique vont revenir suivant la même direction puisqu’ils se confondent avec la normale au point d’incidence.
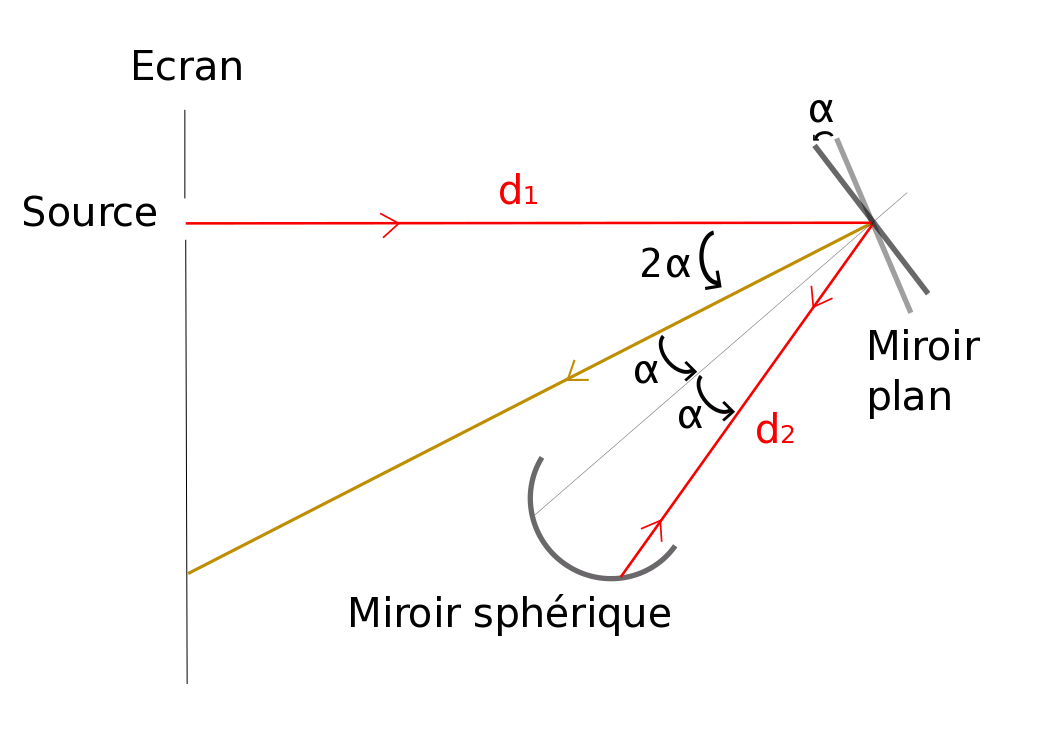
Maintenant le miroir plan est mis en rotation rapide, figure 2. Il a tourné d’un angle α pendant la durée d’aller-retour de la lumière entre le miroir plan et le miroir sphérique. Le rayon lumineux revenant sur le miroir plan est alors dévié d'un angle 2α, selon les lois de Descartes relatives à la réflexion.
Le faisceau retour (en jaune foncé) sera donc légèrement décalé par rapport à la source.
La mesure de ce décalage permet de remonter à la célérité c de la lumière dans l’air en connaissant la vitesse de rotation du miroir et le rayon de courbure du miroir sphérique. Cette mesure sera d’autant meilleure que l’angle α sera grand et donc que la distance entre le miroir plan et le miroir sphérique sera importante.
Lorsque le miroir plan a tourné d’un angle α, la lumière a parcouru la distance 2d2 pendant une durée Δt. Soit c = 2d2 / Δt
Par définition, la fréquence de rotation du miroir plan est N = ω / (2π)
Où ω est la vitesse angulaire du miroir, ω = α / Δt
D'où Δt = α / (2πN)
Finalement, on peut retrouver la vitesse de la lumière :
2. Montage optique
2.1 Choix de la source lumineuse
À son époque, Foucault utilisait un héliostat pour éclairer le miroir tournant, figure 3 à gauche. C’est un dispositif à miroirs qui renvoie la lumière du Soleil, quelle que soit sa position dans une direction donnée. Nous décidons de le remplacer par un laser pour sa grande directivité.
Foucault utilisait une mire transparente (figure 3 à droite) éclairée par l’héliostat dont il projetait l’image grâce à une lentille convergente sur le miroir sphérique. L’image retour de cette image était observée à travers un microscope. La position de la mire lorsque le miroir est au repos était repérée au préalable par une croix.
Nous proposons de remplacer la mire par un spot laser projetée sur papier millimétré dont l'image sera enregistrée par une caméra. Pour effectuer nos mesures avec un bon contraste, nous devons protéger l'écran de la lumière extérieure. Nous utilisons un cercle de papier millimétré collé sur un bout de tuyau de PVC. Nous glissons la webcam dans un autre bout de tuyau pvc et nous raccordons les deux avec un manchon.
2.2 Choix du miroir fixe
L’image de la source S se forme sur le miroir sphérique grâce à une lentille convergente de focale 300 mm, figure 4. Tout comme le montage de l'expérience historique, nous utilisons une lame semi-réfléchissante pour projeter l'image de la source. Il s’agit d’une lame transparente traitée pour laisser passer 50% de la lumière incidente et réfléchir les 50% autres.
Nous souhaitons retrouver la vitesse de la lumière à partir de la relation :
La plus grande dimension de la salle que nous occupons au club de sciences est d'environ 5 m. Nous pouvons raisonner sans tenir compte de la lame semi-réfléchissante car celle-ci a seulement pour effet de modifier la direction d’observation du point S’. En première approximation, nous considérons que le miroir sphérique est suffisamment éloigné (à l'infini) de la lentille convergente donc que le point S’ se trouve au foyer de la lentille convergente.
Nous pouvons écrire, dans l'hypothèse des petits angles : tan(2α) ≈ 2α ≈ ΔS’ / f
D'où, c = 8d2πNf / ΔS'
Et : ΔS' = 8d2πNf / c
Dans l'expérience historique de Foucault, le miroir tournait à 400 tours/seconde. Dans notre salle d'environ 5 m, avec une lentille convergente de focale 300 mm, le décalage ΔS’ est d'environ 5x10-5m soit 50 μm. À moins de travailler dans une salle plus grande, il nous paraît difficile de mesurer un tel décalage. Nous nous sommes alors tournés vers une autre solution.
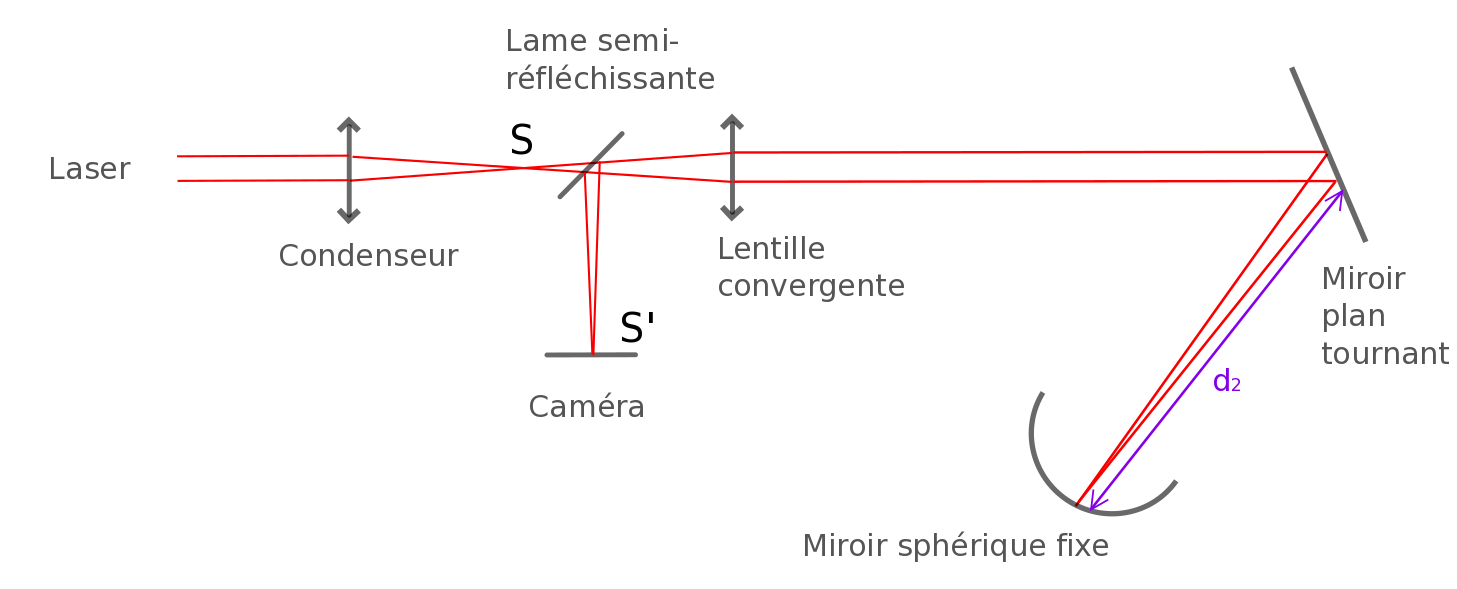
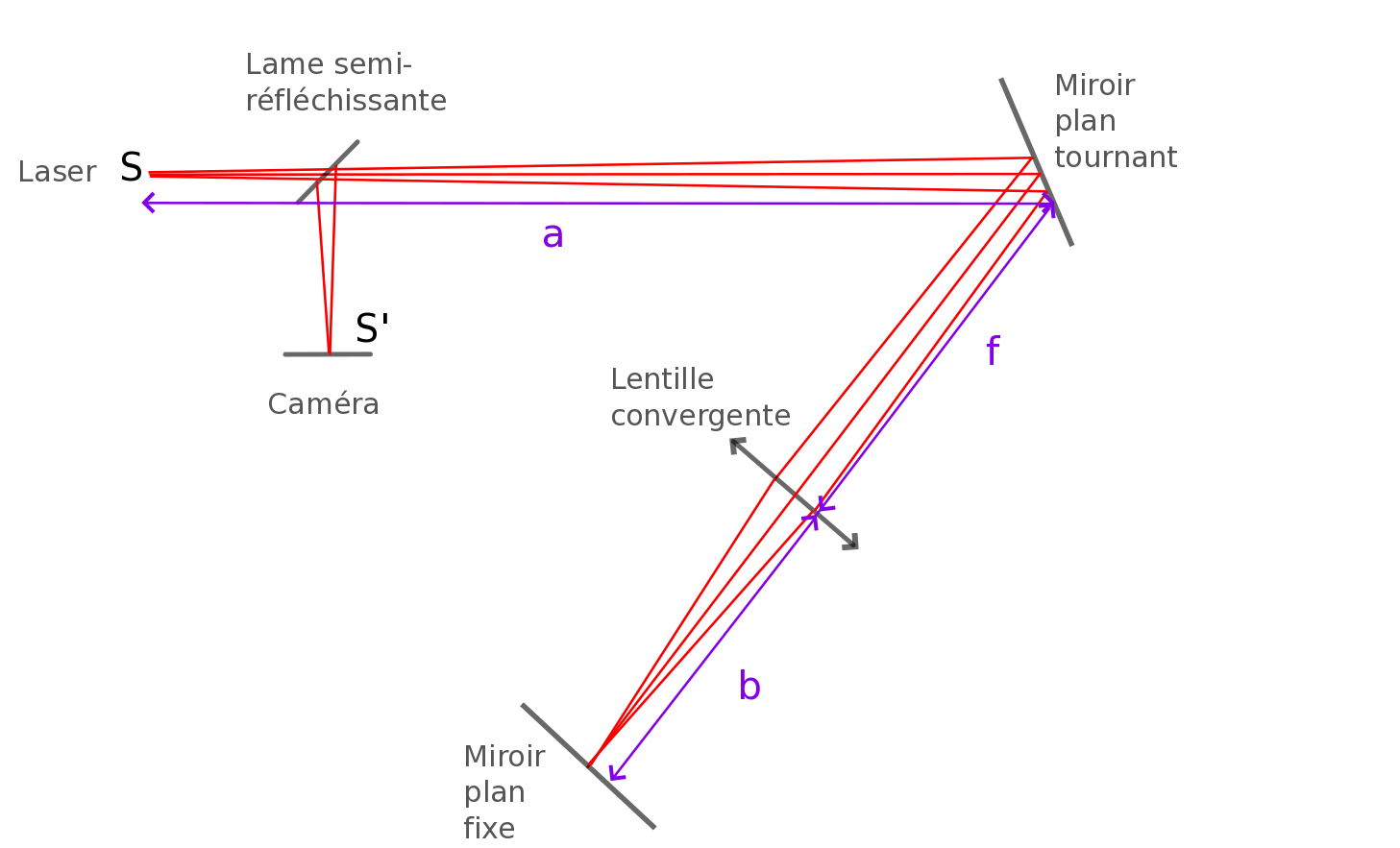
En 1878, le physicien Albert Abraham Michelson a eu l’idée de remplacer le miroir sphérique par un miroir plan fixe, figure 6. Pour que la lumière réfléchie par ce miroir fixe revienne toujours dans la même direction quelle que soit l’orientation du miroir tournant, il plaça le centre du miroir tournant au foyer d’une lentille convergente de façon à ce que l’image de la source se forme sur le miroir fixe.
Le faisceau principal évolue entre la lentille et le miroir fixe parallèlement à l’axe optique de la lentille étant donné que le miroir tournant est dans le foyer de la lentille. Sur le miroir fixe, perpendiculaire à l’axe optique, le faisceau principal se réfléchit sur lui-même et revient par le même chemin au miroir tournant, indépendamment de sa position. Remarque : compte tenu des dimensions du montage, nous n’utiliserons pas de condenseur dans cette partie car une trop grande partie de la lumière issue de S ne serait pas réfléchie par le miroir tournant à cause de la divergence du faisceau.
Avec ce montage, figure 6, la lumière parcourt la distance 2(f+b) pendant que le miroir tournant effectue une rotation d’un angle α pendant la durée Δt d’aller-retour de la lumière entre le miroir tournant et le miroir fixe.
Donc, c = 2(f+b) / Δt
Alors c = 4(f+b)πN / α
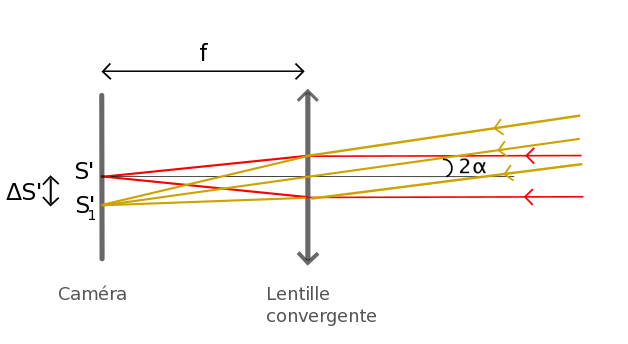
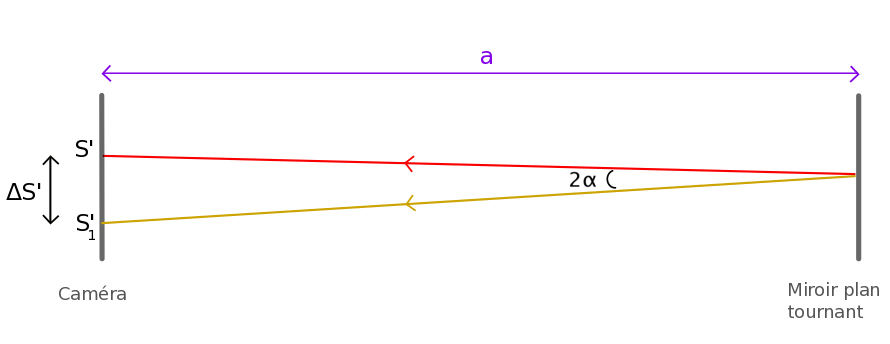
On a maintenant, figure 7, tan2α ≈ 2α (angle petit) ≈ ΔS’ / a
Un déplacement ΔS’ le plus grand possible exige donc une vitesse de rotation N la plus grande possible et une distance a la plus grande possible.
Donc :
Les distances a, b et f sont reliées par la formule de conjugaison des lentilles, figure 6 :
On trouve alors :
Par conséquent, la vitesse de la lumière est donnée par :
On souhaite travailler sur de grandes distances, mais il faut s’accommoder de pertes d’intensité issues de la divergence du faisceau laser. Finalement, on choisit d'utliser la taille de la salle et d'installer le laser et le miroir plan fixe sont côte à côte, donc a = f + b
À l'aide de la formule de conjugaison des lentilles, on a : a = (1 + √2) f et b = √2 f
2.3 Choix de la lentille
Lentille seule
Nous devons choisir une lentille de grande distance focale. De plus, l’image de S étant générée tant que le faisceau venant du miroir tournant est situé dans l’angle d’ouverture de la lentille, lorsque le miroir entre en rotation, la luminosité de l’image de S sera par conséquent d’autant plus forte que la largeur utilisable de la lentille est grande. Il faut donc choisir une lentille de grand diamètre. Au lycée, nous ne disposons que de lentilles de diamètre 40 mm.
La lentille de plus grande focale dont nous disposons au lycée est de 333 mm, ce qui fixe la distance a = (1 + √2) × 0,333 = 80,4 cm.
Pour une vitesse de rotation de 400 tours/s, on a : ≈ 0,02 mm
Une fois encore, la mesure de ce décalage nous semble délicate. À moins d’augmenter la distance focale de la lentille…
Association de lentilles
Notre idée est d’utiliser une combinaison de deux lentilles afin d’augmenter la distance focale et obtenir ainsi un déplacement ΔS’ plus grand. En effet, lorsque l’on accole deux lentilles minces de vergences V1 et V2, la vergence V de l’ensemble est de : V = V1 + V2, si on considère confondus leurs centres optiques.
Rappel : Vergence d'une lentille
Dans le cas d'une lentille dans l'air, la vergence est simplement définie comme l'inverse de la distance focale image.
Nous allons donc utiliser la relation d’addition des vergences en combinant une lentille convergente avec une lentille divergente afin d’obtenir un système optique convergent de plus petite vergence possible. Nous constatons qu’il est théoriquement possible d’obtenir un système de vergence 0,33 δ soit une focale de 3 m environ, en associant une lentille convergente de 300 mm avec une lentille divergente de -333 mm. Avec cette association, le déplacement théorique devient : ΔS’ = 1,76 mm pour une vitesse de rotation du miroir de 400 Hz.
En plaçant notre combinaison de lentilles face au soleil, nous constatons que la distance focale de l’ensemble est bien inférieure à 3 m. Nous l’estimons très grossièrement à 2 m. En effet, les lentilles que nous utilisons possèdent une épaisseur et la distance e entre leur centre n’est donc pas nulle.
Dans ce cas, il faut utiliser la relation de Gullstrand pour calculer la vergence de l’ensemble : V = V1 + V2 – eV1V2
A cause des incertitudes sur les valeurs des vergences des lentilles fournies par le fabriquant et surtout l’incertitude sur la valeur de e, nous choisissons de mesurer la vergence de l’ensemble.
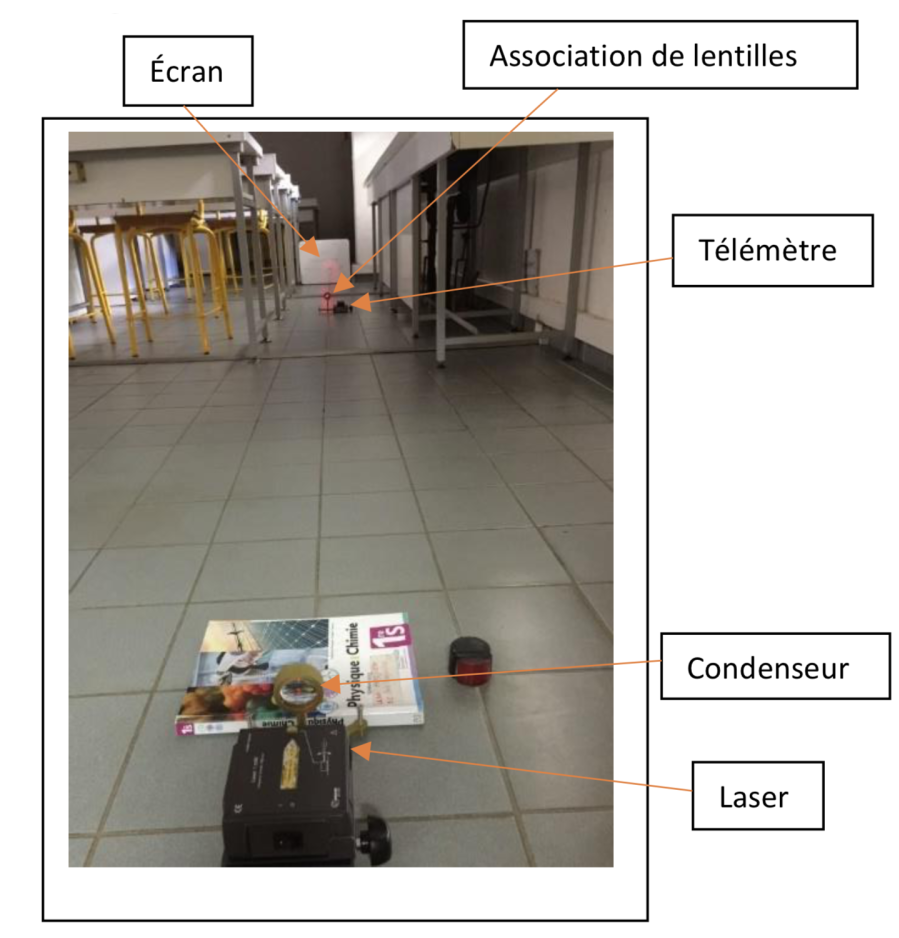
Pour cela, nous plaçons un condenseur (lentille de focale courte de 50 mm) devant un laser afin d’obtenir une source S la plus ponctuelle possible. Nous plaçons notre combinaison de lentilles à une distance x connue de S mesurée au télémètre laser de l’ordre du double de la distance focale de la combinaison. Nous cherchons la position x’ de l’image S’ de S sur un écran. Nous en déduisons f d’après la relation de conjugaison des lentilles.
Nous trouvons f = 1,90 ± 0,01 m à 95%. Ce qui conduit à un déplacement ΔS’ = 0,70 mm pour une vitesse de rotation du miroir de 400 Hz et à un montage dont les dimensions sont : a = (1 + √2) × 1,90 = 4,59 m
3. Conception des supports
Nous avons choisi de recréer les supports d'instruments optique à l'image de ceux utilisés dans l'expérience historique, figure 9a. À l'aide des photos de l'expérience située au Conservatoire National du musée des Arts et Métiers à Paris (CNAM), nous avons fabriqué les pièces, en les modélisant avec le logiciel SOLIDWORKS (figure 9b) puis en utilisant l'imprimante 3D du lycée (figure 9c).
La pièce la plus délicate à réaliser est le support de miroir car l’ensemble « miroir-support-fermoir » doit être parfaitement équilibré pour éviter les vibrations (figure 9d).
Nous avons opté pour un support de miroir tournant dont les axes sont guidés par deux roulements à bille. Le support sera porté par les guides des roulements. Le moteur sera relié au support du miroir par un accouplement flexible pour éviter que les vibrations endommagent les roulements.
Le prototype du miroir tournant imprimé répond aux attentes, mais il ne serait pas prudent de l’utiliser de manière intensive pour des vitesses de rotation élevées, les vibrations risquent de devenir destructrice pour le plastique utilisé (ABS). Le risque de projection de matière n’étant pas nulle, nous nous sommes rapprochés d’un atelier afin de faire usiner la pièce en métal à l'aide des côtes fournies (notre professeur de physique nous a mis en relation avec un ancien professeur de productique enthousiasmé par le projet).
4. Motorisation et pilotage du miroir tournant
4.1 Méthode utilisée historiquement
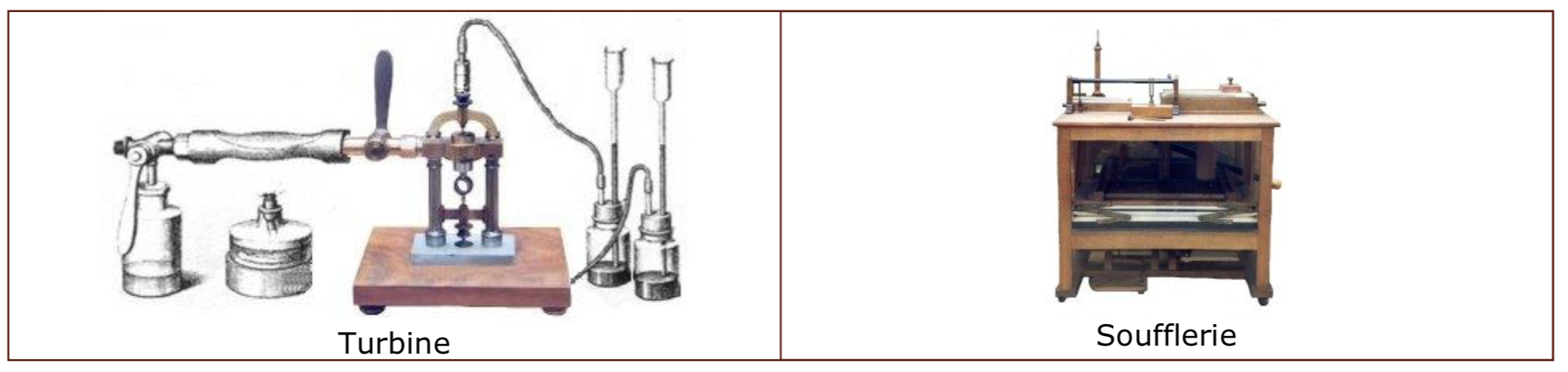
À l’époque, la rotation du miroir est assurée par une turbine, mise au point par Gustave Froment, alimentée par une soufflerie à air comprimé mise au point par Aristide Cavaillé-Coll, figure 10.
Le fonctionnement de l'ensemble est décrit dans cette vidéo du Musée des Arts et métiers : Foucault et la mesure de la vitesse de la lumière, 1862 : le miroir tournant
4.2 Choix du moteur et de sa commande
Le moteur et sa commande sont représentés sur la figure 11.
Figure 11. Motorisation et pilotage du miroir tournant |
- Nous avons choisi d'utiliser un moteur brushless ou « sans balais » (machine synchrone) triphasé couramment utilisé en modélisme. Il est piloté par un courant alternatif triphasé dont on fait varier la fréquence en fonction de la vitesse de rotation souhaitée. Notre choix s'est porté sur un moteur de la marque « XPOWER » de 3540 KV, où le KV représente la vitesse de rotation maximale du moteur à vide par volt.
- La source d'énergie est une batterie LIPO 4S de 14,8 V. La fréquence théorique de rotation N, à vide, maximale sera alors égale à : N = 3540 x 14,8 / 60 = 873 tours/seconde.
- Le contrôle de la vitesse est assuré par un ESC ou « Electronic Speed Controler ». Il peut générer un courant alternatif triphasé dont la fréquence varie en fonction de la vitesse de rotation souhaitée.
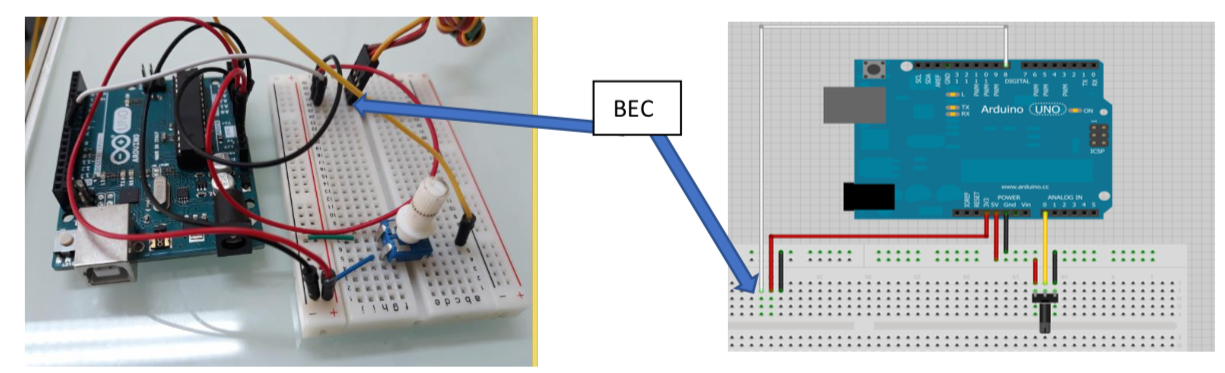
- Le BEC « Batterie Eliminator Circuit » est un régulateur de tension. La source d'énergie est une pile donc une alimentation continue, à l'aide du BEC, piloté par l'interface Arduino, nous allons générer un signal alternatif pour chacune des phases du moteur.
La sortie du BEC se compose de 2 fils correspondant à l'alimentation (noir et rouge) et d'un fil pour la partie commande (représenté en blanc), figure 12.
Figure 12. Commande de la vitesse du moteur |
Le pilotage se fait grâce à un potentiomètre relié au PIN A0. Le signal électrique est numérisé par le CAN du microcontrôleur puis converti (« maping ») en signal lu par l’ESC. Le programme Arduino de pilotage du moteur est fourni en annexes.
4.3 Fréquencemètre
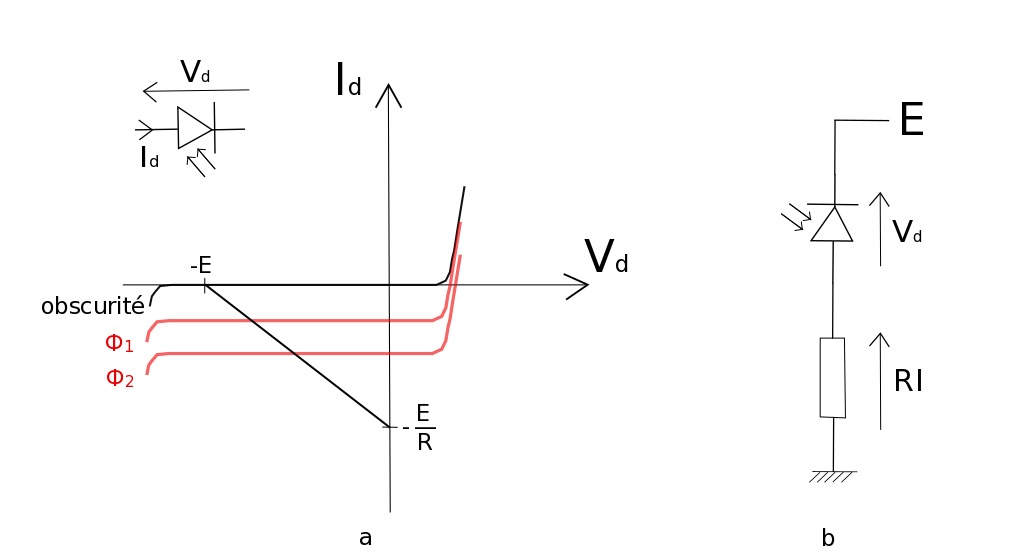
Pour retrouver la valeur de la vitesse de la lumière, il est nécessaîre de connaître avec précision la vitesse de rotation du moteur. Nous avons utilisé une photodiode polarisée en inverse, et se servir du fait qu'elle délivre un courant sortant de son anode lorsqu'elle est éclairée, figure 13a.
La photodiode polarisée en inverse délivre un courant lorsqu'elle est éclairée. D’après la loi d’Ohm, en reliant la photodiode à une résistance, on obtient, aux bornes de la résistance, une tension électrique proportionnelle au courant délivré, figure 13b.
On éclaire le miroir tournant avec le laser et on l’oriente de manière à ce que le faisceau réfléchi éclaire la photodiode à chaque tour.
Pour obtenir directement la fréquence de rotation du miroir, nous lisons la tension aux bornes de la résistance sur le TIMER de la PIN 5 du microcontrôleur. Ce TIMER 16 bits sera incrémenté sur des fronts montants pendant une seconde puis remis à zéro. La valeur de l’incrémentation qui correspond à la fréquence de rotation du moteur sera affichée sur un écran LCD.
Le programme Arduino du fréquencemètre est fourni en annexes.
5. Mesures de la vitesse de la lumière
5.1 Étalonnage de l'écran
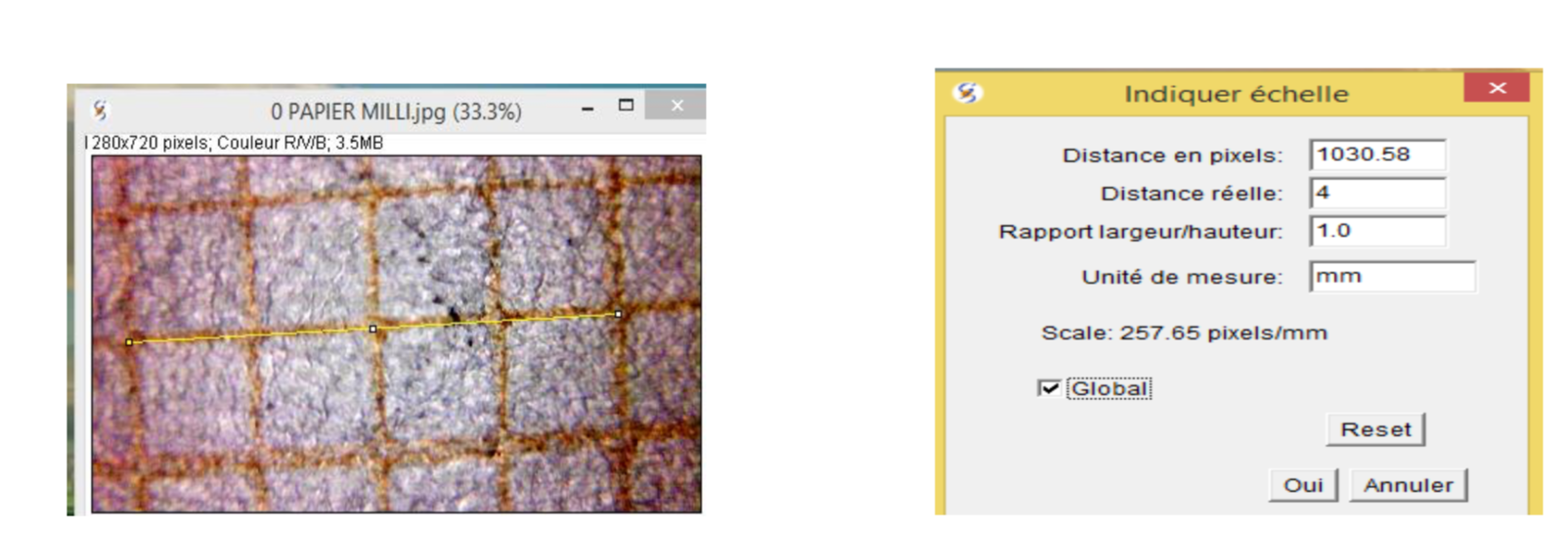
On photographie l’écran avec un éclairage blanc et on étalonne l’image avec le logiciel SALSAJ, figure 14.
Figure 14. Correspondance pixel/mm de la mire |
5.2 Mesures
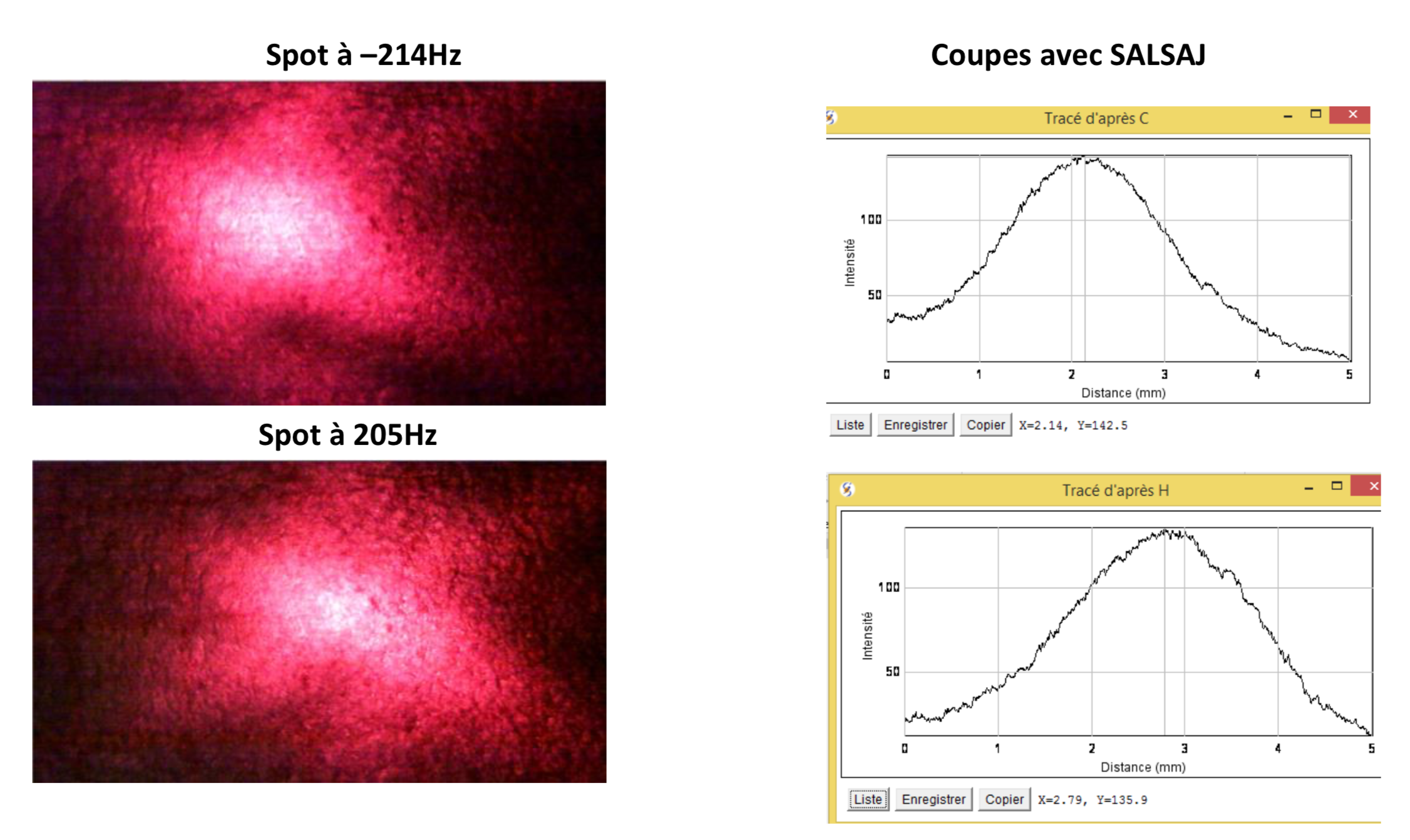
Afin d'obtenir la valeur la plus précice sur la vitesse de la lumière, nous avons réalisé plusieurs photographies du spot lumineux pour différentes fréquences du miroir tournant et dans les deux sens de rotation.
Pour chaque photographie du spot on réalise une coupe à deux dimensions avec le logiciel SALSAJ, figure 15.
Pour déterminer l’incertitude type de la position S’1 du spot, nous avons estimé un encadrement de sa position (S’1 max-S’1 min) et nous estimons l'incertitude type :
(S’1 max-S’1 min) / (2√3)
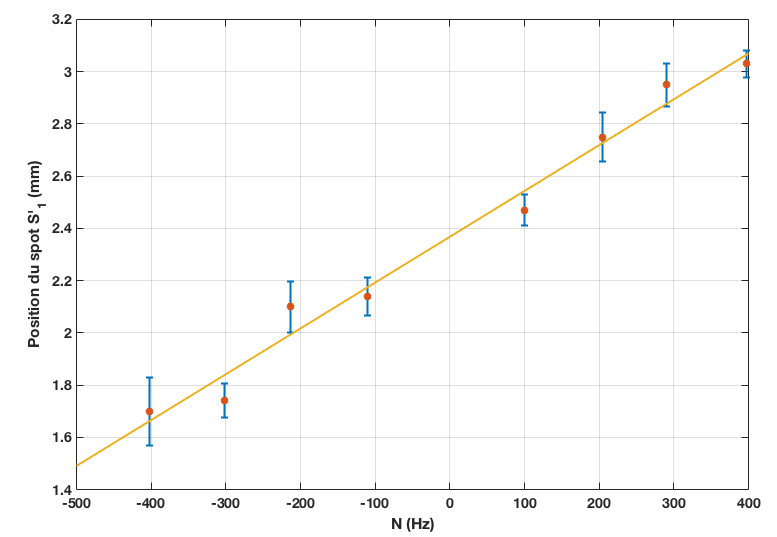
Nous avons ensuite tracé la courbe de la position S’1 du centre du spot en fonction de la fréquence de rotation du miroir, figure 16.
Remarque : L’incertitude sur la lecture de la fréquence est estimée par rapport aux légères fluctuations de l’affichage de l’écran LCD pendant la mesure 5 / (2√3) ≈ 1,4 Hz.
Après modélisation, nous obtenons une relation affine : S’1 = kN + S’
Nous en déduisons la position S’ du centre du spot lorsque le miroir est à l’arrêt : 2,37 mm et le coefficient k = (1,75 ± 0,24) x 10-6 m.s
D'où ΔS’ = kN
À partir de la relation c = 8πNf(2a+f) / ΔS’, nous en déduisons : c = 8πf(2a+f) / k
Ce qui donne numériquement : c = 8πx1,90x(2x4,59+1,90) / (1,75x10-6) = 302 000 km/s
Soit un écart relatif de 0,7% par rapport à la valeur théorique (299 792 km/s).
6. Conclusion
Pour conclure, nous pouvons dire que ce projet a été très enrichissant et nous a beaucoup apporté. Nous avons appris à travailler en équipe. Nous nous sommes confrontés à de réelles difficultés expérimentales. Nous nous sommes parfois sentis dans la peau de ce génial physicien qu’était Léon Foucault lorsqu’il essayait de mettre en œuvre son expérience et avons pu réaliser à quel point il faut être persévérant afin d’obtenir des mesures exploitables.
Comme perspectives, nous envisageons de fabriquer un récipient transparent suffisamment long pouvant contenir de l’eau afin de mesurer la vitesse de la lumière dans l’eau comme Foucault l’avait fait à l’époque afin de valider la théorie ondulatoire de propagation de la lumière.
Annexes
- Programme Arduino de commande du moteur : controle_moteur_brushless.ino
- Programme Arduino du fréquencemètre : Frequencemetre_LCd_analyse.ino
[1] Thèse de physique soutenue par Léon Foucault le 25 avril 1853, « Sur les vitesses relatives de la lumière dans l'air et dans l'eau ». Source : The Internet Archive
Pour citer cet article :
Mesure de la vitesse de la lumière par l'expérience historique de Foucault, avril 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Foucault-mesure-vitesse-lumiere.xml