Les satellites JASON et la mesure du niveau des océans

La surface des mers et des océans révèle une grande diversité de phénomènes. Elle est agitée par les vagues et la houle et le niveau de l'eau varie selon plusieurs échelles de temps : en quelques heures sous l'effet des marées ou de la pression atmosphérique ; en quelques jours du fait de la circulation océanique tourbillonnaire ; en quelques mois selon les saisons (dilatation thermique) ; sur plusieurs années sous l'effet des variations climatiques. Ces variations du niveau des mers sont de l'ordre de quelques centimètres à plusieurs mètres. Les différences de niveau d'une région géographique à l'autre sont du même ordre sur des échelles de distances variées.

Les satellites altimétriques permettent de mesurer les variations spatiales et temporelles de la « topographie de surface des océans » sur des échelles de temps supérieures à 10 jours et des échelles d'espace supérieures à 100 km environ.

Un exemple d'application de l'altimétrie est le suivi du niveau moyen mondial des océans (Mean Sea Level, MSL) car sa variation lente est un important signal relié aux modifications du climat de la planète. On la détecte à partir de nombreuses mesures de niveaux des mers, moyennées sur de grandes surfaces (100 à 1000 km) et sur de longues durées (années).

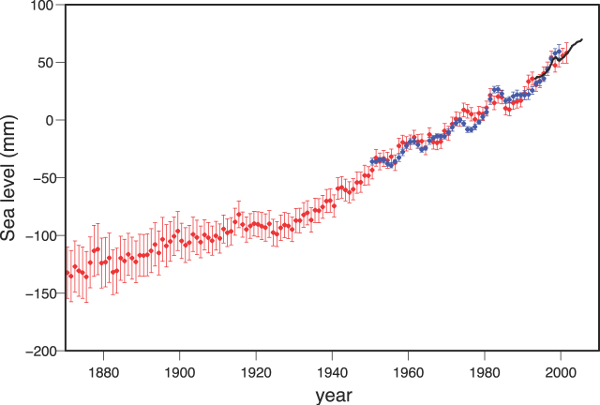
Les figures 1 et 2 représentent cette variation. On observe une augmentation du niveau moyen des océans, avec une pente de l'ordre de +2 à +3 mm par an.

La figure 1 résume la variation relative du niveau moyen des mers sur plus d'un siècle. Elle est établie par le groupe de travail du GIEC 2007* chargé de rassembler les données scientifiques liées aux évolutions du climat. On remarquera que la pente de cette courbe a tendance à augmenter.

http://www.ipcc.ch/graphics/ar4-wg1/jpg/fig-5-13.jpg

En rouge : reconstruction des niveaux de zones de la mer ; en bleu : mesure des marégraphes ; en noir : altimétrie par satellite depuis 1992. Les niveaux sont donnés en millimètres par rapport à la moyenne des années 1961 à 1990. Les barres d'erreur sont à 90% de confiance.

Figure du rapport du Groupe de Travail I (wg1) du GIEC 2007, « Les éléments scientifiques », résumé technique, page 50. Le document complet en français est téléchargeable depuis le lien : http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-ts-fr.pdf (18,2 M)

Source : http://www.ipcc.ch/graphics/ar4-wg1/jpg/fig-5-13.jpg, accessible depuis http://www.ipcc.ch/publications_and_data/ar4/wg1/fr/tssts-3-3-3.html

Figure 1. Moyennes annuelles du niveau moyen mondial de la mer

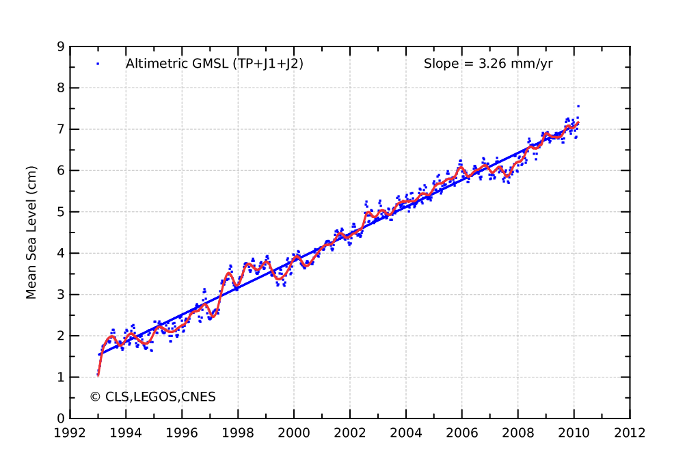
La figure 2 détaille les résultats des mesures obtenues depuis 1992 grâce à l'altimétrie par radar embarqué sur satellite.

http://www.aviso.oceanobs.com/fr/actualites/indicateurs-des-oceans/niveau-moyen-des-mers/index.html

Résultats des missions altimétriques Topex/Poséidon, Jason-1 et désormais Jason-2.

Le niveau moyen est obtenu après avoir retiré les signaux annuel et semi-annuel. Les points bleus et la courbe rouge correspondent à des moyennes sur 2 et 6 mois. Après correction du rebond post-glaciaire (-0,3 mm/an), on estime l'élévation du niveau moyen des mers à 3,26 mm/an, l'incertitude sur cette pente étant de 0,6 mm/an pour un intervalle de confiance de 90% (Crédits CLS/Cnes/Legos).

Source : http://www.aviso.oceanobs.com/fr/actualites/indicateurs-des-oceans/niveau-moyen-des-mers/index.html

Figure 2. Évolution du niveau moyen des mers vu par les altimètres

La comparaison des figures 1 et 2 montre que l'altimétrie par satellite a permis d'améliorer d'un ordre de grandeur environ la précision des mesures du niveau moyen de la mer. La précision atteinte étant maintenant de l'ordre du cm.

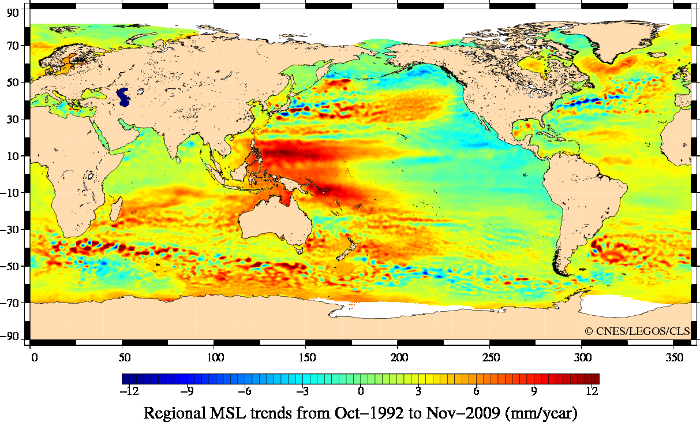
Remarquons que même si la tendance globale est à l'élévation du niveau moyen des océans, il existe des différences régionales importantes (entre -10 et +10 mm/an) comme le montre la figure 3.

http://www.aviso.oceanobs.com/fr/actualites/indicateurs-des-oceans/niveau-moyen-des-mers/index.html

La carte ci-dessus représente les données de plusieurs missions depuis 1993, permettant une bonne résolution de l'estimation des pentes locales. Des variations ponctuelles du niveau moyen sont ainsi mises en évidence, principalement dans les grands courants océaniques. (Crédits CLS/Cnes/Legos).

Source : http://www.aviso.oceanobs.com/fr/actualites/indicateurs-des-oceans/niveau-moyen-des-mers/index.html

Figure 3. Répartition géographique de la variation du niveau moyen des mers vu par les altimètres, entre 1992 et 2009

Dans la suite, nous décrivons brièvement la méthode de l'altimétrie par satellite, puis nous explicitons quelques contraintes techniques et principes physiques mis en jeu, compte tenu des objectifs requis pour la surveillance globale du niveau des océans : la précision des mesures, la couverture temporelle et spatiale, l'acquisition et l'analyse statistique des données.

On soulignera les performances réalisées par la plus récente mission altimétrique, celle du satellite Jason-2, lancé en juin 2008, fruit d'une collaboration entre la France et les Etats-Unis (sites : http://smsc.cnes.fr/JASON2/Fr/ et http://jason2-cnes.fr/).

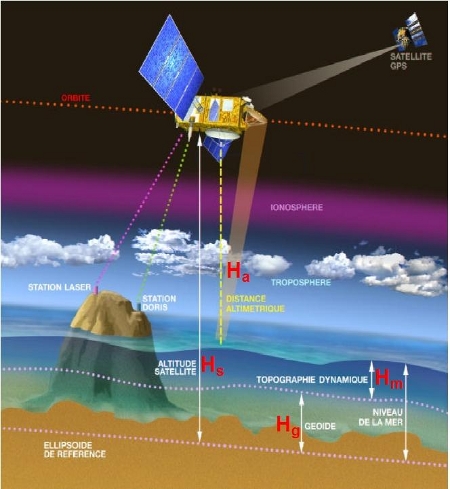
On mesure le temps de retour d'une onde émise par le satellite après réflexion sur la surface de la mer. Un radar embarqué sur le satellite émet verticalement des ondes radio, sous forme de brèves impulsions. Les ondes se réfléchissent sur la surface des océans. L'écho de chaque impulsion est détecté et analysé à bord du satellite, ce qui conduit à une détermination précise de la distance « altimétrique », c'est-à-dire la distance H_a entre le satellite et le niveau de la mer. En fonction de la durée T d'aller-retour du signal radar et de la célérité c de propagation de l'onde, on a 2 H_a = c T.

La figure 4 illustre ce principe et schématise la géométrie d'une mesure : Hs est l'altitude du satellite au dessus de « l'ellipsoïde de référence », Ha la distance « altimétrique » mesurée par le radar. On en déduit la valeur relative Hm du niveau de la mer, celle qui concerne la « topographie dynamique » par : Hm = Hs - Ha - Hg (relation 1) La correction Hg est une distance, de l'ordre de la centaine de mètres, qui dépend du lieu de la mesure. C'est l'écart entre le « géoïde », c'est-à-dire la surface équipotentielle de la gravité terrestre (niveau de repos de la mer) et l'ellipsoïde de référence par rapport auquel est repéré le satellite (voir partie « Ellipsoïde de référence et géoïde »). Le « Service d'Altimétrie et Localisation Précise » du CNES a réalisé une animation qui décrit le principe de l'altimétrie radar par satellite (fichier .exe exécutable DOS/Windows, 6.7 Mo).

http://www.aviso.oceanobs.com/fr/altimetrie/principe/principe-de-base/index.html D'après http://www.aviso.oceanobs.com/fr/altimetrie/principe/principe-de-base/index.html Figure 4. Principe de l'altimétrie

La valeur absolue de H_g n'est pas déterminée partout avec une précision suffisante pour déduire H_m de la relation (1). C'est pourquoi on répète de nombreuses fois la mesure radar aux mêmes points de passage du satellite et on détecte les variations relatives de H_m par rapport à une valeur moyenne. Sur les figures 1 et 2, l'origine H_m = 0 est fixée à la moyenne des années 1961 à 1990. Pour déterminer la variation de H_m avec une précision meilleure que le centimètre, les deux termes H_s et H_a doivent être déterminés avec une précision au moins équivalente. Par exemple, le satellite Jason-2 gravite à une altitude H_s égale à 1336 km et sa localisation doit donc être assurée avec une erreur relative inférieure à 10^-5.

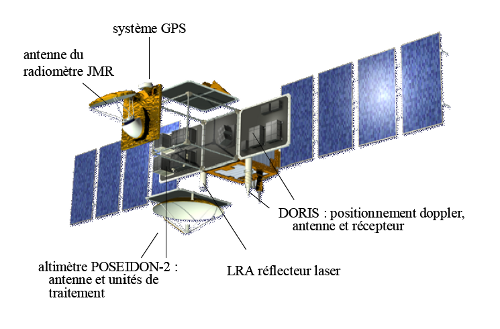
Le satellite Jason-1, représenté sur la figure 5 comporte, outre l'altimètre Poséidon-2, plusieurs autres instruments. Pour le positionnement : le système français DORIS (Doppler Orbitography and Radiopositionning Integrated by Satellite) constitué d'un réseau de 50 balises au sol, détermine en permanence avec précision la position et la vitesse du satellite. En complément on utilise des mesures d'un système américain de GPS (Global Positioning System) embarqué, ainsi que des pointages très précis par tirs laser à partir du sol sur le réflecteur du satellite (LRA). Le radiomètre JMR (Jason Microwave Radimeter) sert à évaluer l'influence de la traversée de l'atmosphère sur le temps T de parcours de l'onde (voir partie « Transmission du rayonnement par l'atmosphère »).

http://www.aviso.oceanobs.com/fr/missions/missions-actuelles/jason-1/instruments/index.html

D'après http://www.aviso.oceanobs.com/fr/missions/missions-actuelles/jason-1/instruments/index.html

Figure 5. Les instruments du satellite Jason-1

L'orbite du satellite est choisie de façon à optimiser la répétition des mesures sur la plus grande partie possible de la surface du globe. L'altitude de 1336 km est assez élevée pour que le satellite ne soit plus sensible aux frottements sur le gaz atmosphérique résiduel, ni aux fluctuations de la gravité liées aux reliefs terrestres. La stabilité de l'orbite permet de situer avec précision la position du satellite, sa hauteur H_s et sa trace au sol en longitude et latitude.

L'orbite est circulaire, son plan est incliné de 66 degrés sur le plan équatorial, ce qui permet de balayer une large zone de la surface terrestre, entre les latitudes + 66° et - 66°. La période de rotation du satellite est de 112 minutes et à chaque tour sa trace verticale sur la surface terrestre est décalée de 315 km à l'équateur. Le satellite repasse sur le même point au sol au bout de 9,9156 jours. Ceci réalise un bon échantillonnage temporel et spatial des mesures.

La figure 6 représente sur une carte mondiale la trace au sol du satellite pendant un cycle de 10 jours. La durée entre deux passages est calculée pour ne pas coïncider avec un multiple de la périodicité des jours ou des marées, de façon à éliminer les fréquences correspondantes dans la répétition des mesures (effet de stroboscopie ou « aliasing »). Le choix de l'orbite de Jason-2 est le même que pour les missions précédentes Topex/Poséidon lancé en 1992 et Jason-1 en 1999.

Légende originale : T/P, Jason-1 and OSTM/Jason-2 ground track coverage every 10 days

Source : figure 11, SALP-MU-M-OP-15815-CN, Ed 1.4, July 2009, OSTM/Jason-2 Products Handbook, pdf version (1M) http://www.aviso.oceanobs.com/fr/donnees/boite-a-outils/manuels-d-utilisation-des-donnees-aviso/index.html

Figure 6. Traces au sol du satellite altimètrique sur le cycle de 10 jours

Les systèmes de localisation du satellite doivent être très performants pour suivre en permanence la trajectoire du satellite avec une précision de l'ordre du centimètre.

Toutes les données de repérage sont intégrées dans un calcul élaboré d'orbite qui fournit à chaque instant la distance verticale précise H_s entre le satellite et « l'ellipsoïde de référence ».

L'ellipsoïde de référence définit un repère du référentiel terrestre : c'est un ellipsoïde de révolution autour de l'axe des pôles, centré sur le centre de masse de la terre et de demi-axes égaux à 6378 km (rayon de l'équateur) et 6357 km (demi-petit-axe d'un méridien). L'ellipsoïde n'est pas exactement une surface équipotentielle du champ de gravité.

Au niveau du sol terrestre et de la surface des océans, on observe que le vecteur gravité g est différent d'une région à une autre et dévie de la normale à l'ellipsoïde, en raison des reliefs et de l'inhomogénéité des sous-sols (les détails et modèles sur la gravimétrie et la détermination du géoïde sont donnés dans l'article « Gravimétrie et géodésie : principes, applications » du site Planet-Terre). Par exemple la figure 7 montre comment une masse locale modifie l'équipotentielle de gravité.

Le cas 1 et 4 représentent un creux et une bosse topographiques du fond de l'océan. Les cas 2 et 3 représentent la présence d'une masse moins dense (sel, eau, pétrole...) ou plus dense (minerai de fer, or, platine...) que l'encaissant (Crédits Planet-Terre, ENS de Lyon).

Figure 7. Perturbation de la surface océanique, équipotentielle de gravité

Les mesures précises de l'accélération g de la pesanteur, la gravimétrie, sont également effectuées par satellite, comme le font par exemple la mission américaine GRACE (Gravity Recovery and Climate Experiment) dédiée aux variations temporelles de g et la mission européenne GOCE (Gravity field and steady-state Ocean Circulation Explorer) qui vise à améliorer la résolution spatiale.

La combinaison des mesures gravimétriques et altimétriques permet de déterminer le géoïde, la surface équipotentielle d'altitude nulle qui est celle qu'aurait l'ensemble des océans recouvrant la terre en l'absence de tout mouvement marin ou atmosphérique. Différents centres de données fournissent des modèles et cartes des écarts du géoïde par rapport à l'ellipsoïde de référence.

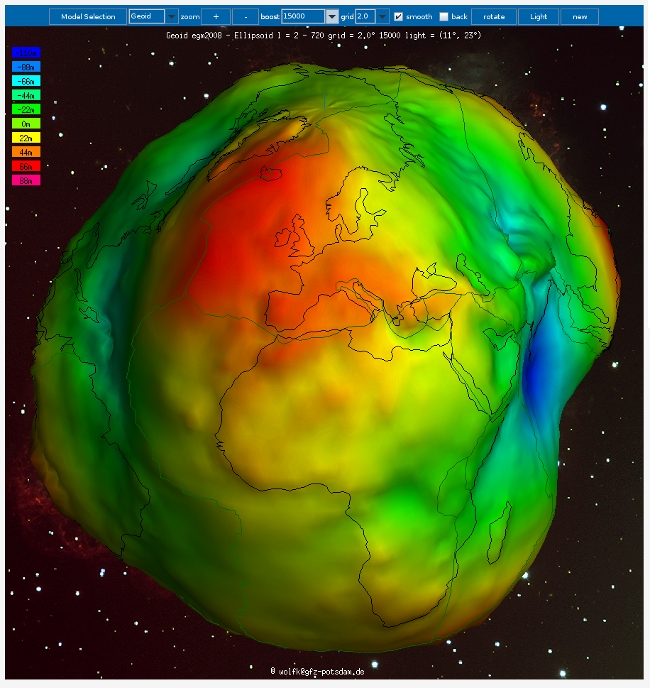
L'illustration de la figure 8 donne un exemple de représentation du géoïde sur l'ensemble de la surface terrestre : les déformations sont très exagérées puisque les codes de couleurs représentent des écarts H_g au plus de l'ordre d'une centaine de mètres. Le facteur d'amplification est ici de 15 000.

Source : International Centre for Global Earth Models, http://icgem.gfz-potsdam.de/ICGEM/ICGEM.html, onglet Visualization

Figure 8. Représentation des ondulations du géoïde

Le radar du satellite envoie une succession d'impulsions brèves et enregistre les signaux reçus en écho après réflexion des ondes incidentes sur la surface de la mer.

La fréquence de l'émission radar est f = 13,576 GHz (bande Ku). La durée des impulsions est de τ = 3 ns. La longueur d'onde λ = c/f = 2,21 cm et le train d'onde émis a donc une longueur de 90 cm (près de 41 oscillations).

L'ouverture angulaire totale de l'onde émise vaut θ = 1,3 degré (cf. note ci-dessous). L'onde couvre donc sur le sol une surface circulaire maximum de diamètre D = H_aθ (avec H_a ≈ H_s = 1336 km, D ≃ 15 km).

L'écho est reçu par le satellite avec un retard T = 2 H_a/c voisin de 9 ms. La mesure précise de cette durée nécessite une analyse fine du signal réfléchi reçu en écho par le satellite.

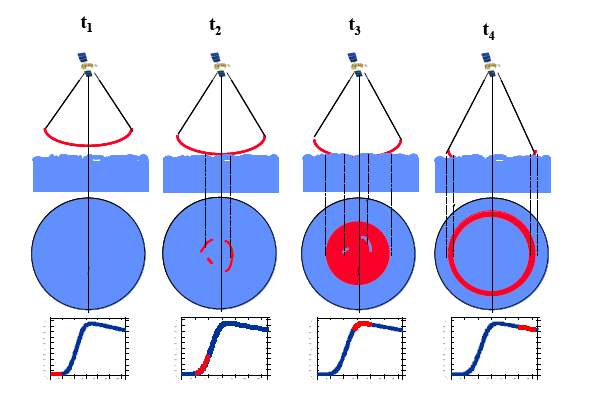
La forme de l'onde réfléchie est modifiée par rapport à l'impulsion incidente émise par l'altimètre du satellite. D'une part le front de l'onde atteint la surface de la mer à différents instants successifs et se réfléchit sous des incidences légèrement différentes, d'autre part la surface de la mer n'est pas parfaitement plane. Ceci est illustré schématiquement par la figure 9.

On voit que l'intensité de l'écho augmente rapidement entre les instants t₂ et t₃. L'intensité diminue lentement entre t₃ et t₄ lorsque ce sont les bords de la surface d'impact du front d'onde qui réfléchissent l'onde vers le satellite.

http://www.aviso.oceanobs.com/fr/altimetrie/principe/impulsions-et-formes-d-onde/index.html

Figure 9. Schéma illustrant l'onde radar atteignant la surface de la mer et les variations en fonction du temps du signal reçu en écho

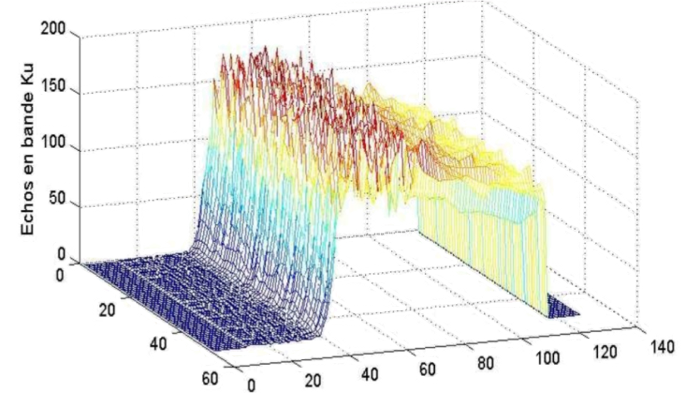
La houle et les vagues produisent des irrégularités dans la durée de retour de l'onde écho. Par exemple un creux de δz = 1 m provoque un retard δτ = 2δz/c = 6,7 ns. Il en résulte des fluctuations du signal d'écho, comme observé sur l'exemple de la figure 10.

Les différentes courbes représentent en fonction du temps les échos des impulsions radar, mesures successives à une cadence de 20 Hz. En fait chaque trace est déjà la moyenne de 100 échos élémentaires, puisque l'altimètre émet 2000 impulsions par seconde. L'échelle 0-140 est un échantillonnage en temps, en pas de 3,25 ns. Chaque écho est échantillonné sur 128 points. La fenêtre temporelle d'écoute du radar, d'une durée totale de 128x3,25 ns, correspond à la durée t₄ - t₁ du schéma de la figure 9.

Figure 10. Exemple réel d'une succession de 50 signaux d'écho enregistrés par l'altimètre

La mesure de la distance altimètrique H_a doit être corrigée des faibles variations de la vitesse de propagation de l'onde radar en fonction de l'altitude à travers l'atmosphère. En effet l'indice de l'air n'est pas exactement égal à l'indice du vide n=1. Dans la troposphère sa valeur, voisine de 1,0003 au sol, dépend des conditions de pression et température, ainsi que de l'humidité. Plus haut, dans l'ionosphère, l'indice est sensible à la présence des électrons libres.

Les écarts de la vitesse de propagation du rayonnement radar par rapport à la vitesse dans le vide nécessite une correction sur H_a déterminé par 2 H_a = c T. Elle est de l'ordre de 1 à 10 cm. Elle est déduite des données météorologiques selon des modèles mis à jour et publiés (voir par exemple l'European Centre for Medium-Range Weather Forecasts, ECMWF).

Cependant la correction due à la quantité d'eau dans la troposphère (vapeur d'eau, nuages...) a une influence très locale. C'est le rôle du radiomètre AMR du satellite Jason de mesurer le contenu en eau de l'atmosphère au point de mesure précis de l'altimètre afin d'en déduire la correction de « troposphère humide ».

La précision des données altimétriques dépend de quatre facteurs principaux : le positionnement du satellite, la mesure de l'altimètre, la transmission de l'atmosphère et l'état de la mer.

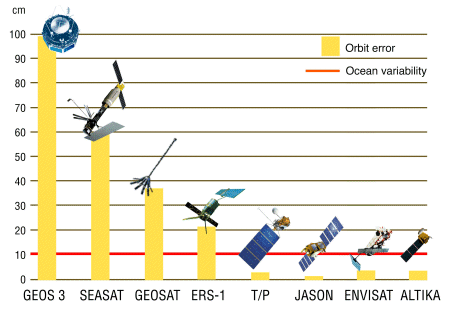
Le tableau suivant cite les principales récentes missions spatiales destinées à l'altimétrie marine pour la surveillance globale du niveau des océans. Elles font l'objet de coopérations internationales dans lesquelles la France est fortement engagée via le CNES (Centre National d'Etudes Spatiales) et le réseau de distribution des données AVISO. Les performances ont progressé d'une mission à l'autre comme le schématise la figure 11.

http://www.aviso.oceanobs.com/fr/missions/missions-passees/index.html

Légende originale : La précision de la mesure depuis les premières missions altimétriques est améliorée d'un facteur 4 depuis 1992 (Crédits Cnes).

Source : http://www.aviso.oceanobs.com/fr/missions/missions-passees/index.html

Figure 11. Précision des mesures altimétriques du niveau moyen des mers

La prochaine mission altimétrique de la série TOPEX-Jason sera Jason-3 en 2013. Les applications des mesures altimétriques sont nombreuses et importantes dans le contexte de la surveillance écologique de la planète, de l'évolution climatique et du développement des régions côtières.

Pour en savoir plus : http://www.aviso.oceanobs.com/fr/applications/