Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Simulations du phénomène de polarisation
16/12/2022
Résumé
Cet article propose des simulations et animations sur le phénomène de polarisation. Il donne accès aux éléments créés pour la vidéo de la Physique animée « Qu'est-ce que la polarisation de la lumière ? ».
Table des matières
1. Introduction
La lumière est une onde électromagnétique, associée à la propagation d’un champ électrique et d'un champ magnétique.
La direction de propagation de la lumière est évidemment une propriété essentielle, mais les directions de son champ électrique et de son champ magnétique sont également très importantes : c’est, plus particulièrement, la direction du champ électrique qui caractérise ce que l’on appelle la polarisation de la lumière.
La notion de polarisation est issue des travaux du physicien Etienne Malus qui, en 1809, a mis en évidence que la lumière réfléchie par une surface vitreuse pouvait être polarisée rectilignement et parallèlement à cette surface.
L’œil humain n’y est guère sensible et pourtant la polarisation de la lumière est un phénomène très courant dans la nature et dans les nouvelles technologies qui nous entourent au quotidien.
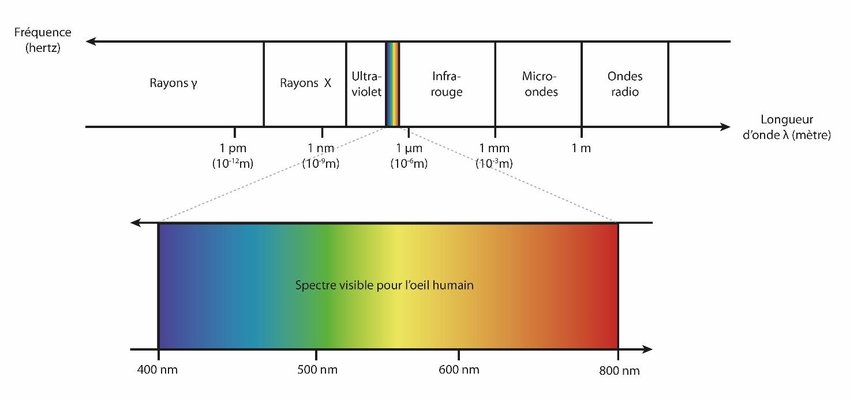
La lumière visible est une onde électromagnétique dont la longueur d’onde dans le vide \( \lambda \) est comprise entre 400 nm pour le violet, et 800 nm pour le rouge.
Une onde lumineuse est physiquement associée à la propagation d’un champ électrique et d’un champ magnétique qui vibrent à des fréquences, notées \( \nu \), très élevées, de l’ordre de 1015 Hz et reliées à la longueur d’onde selon \( \nu = \frac{c}{\lambda}\) où \( c \) est la vitesse de la lumière dans le vide.
La lumière naturelle, comme celle du Soleil par exemple, n'est pas polarisée. Le champ électrique de l’onde électromagnétique émise par le Soleil oscille dans une certaine direction durant une fraction de période puis saute brusquement vers une nouvelle direction aléatoire, tout en restant perpendiculaire à la direction de propagation. Il en est de même pour la lumière émise par une ampoule ou un néon.
2. Polarisation rectiligne d'une onde électromagnétique
Commençons par le cas simple dans lequel le champ électrique garde une direction constante. On dit que la lumière possède une polarisation rectiligne, qui peut être verticale ou horizontale.
Le vecteur champ électrique peut s’écrire, pour une onde plane progressive et monochromatique polarisée selon l’axe (Ox) et se propageant selon l’axe (Oz), sous la forme :
$$ \overrightarrow{E(z,t)} = E_0 \cos(\omega t - k_z). \overrightarrow{u_x} $$
Où \( \omega\) est la pulsation du champ électrique, reliée à la fréquence par \( \omega = 2 \pi \nu \) t k le vecteur d’onde, donné par \( k = \frac{\omega}{c} \) encore appelée pulsation spatiale.
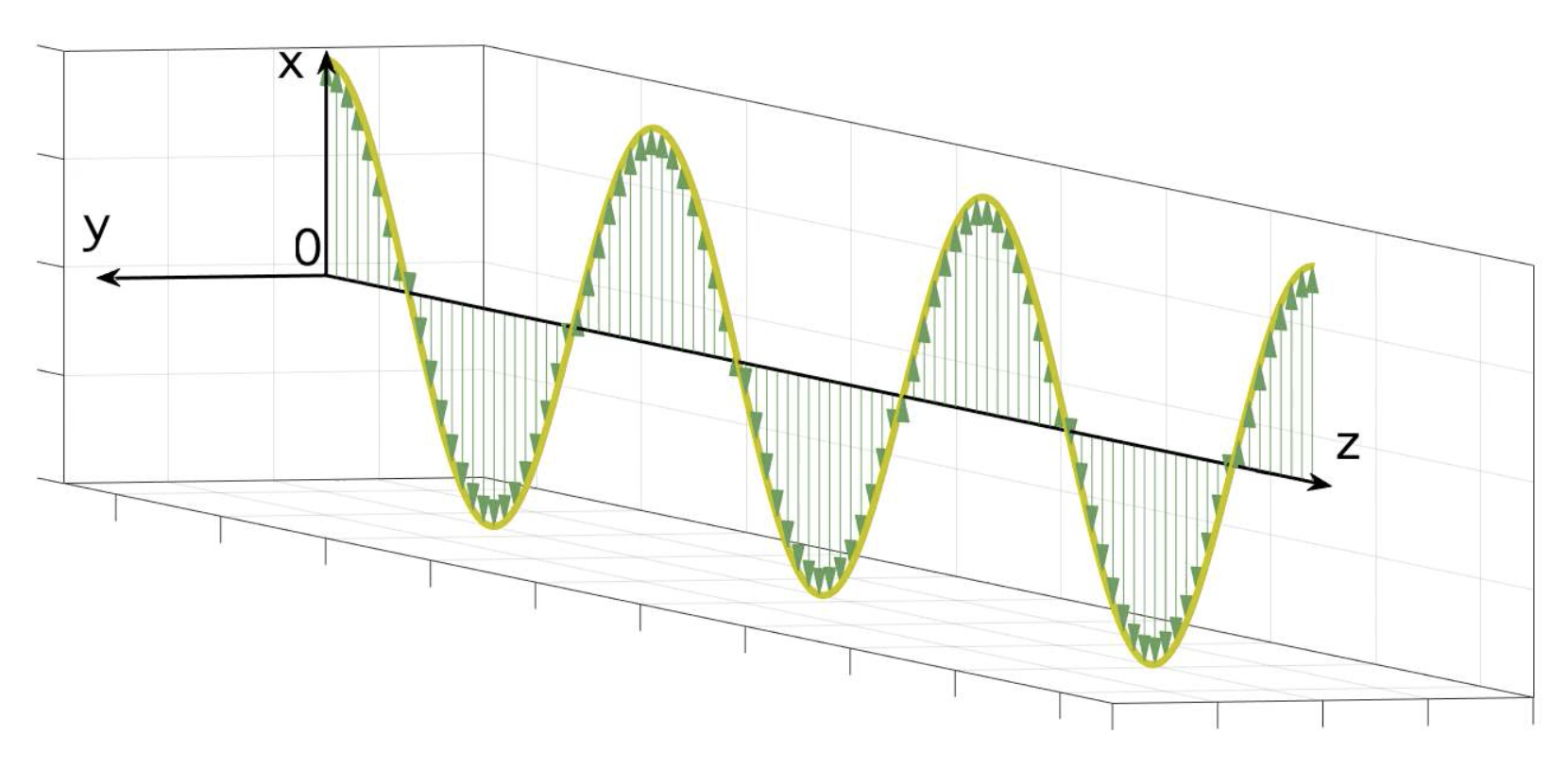
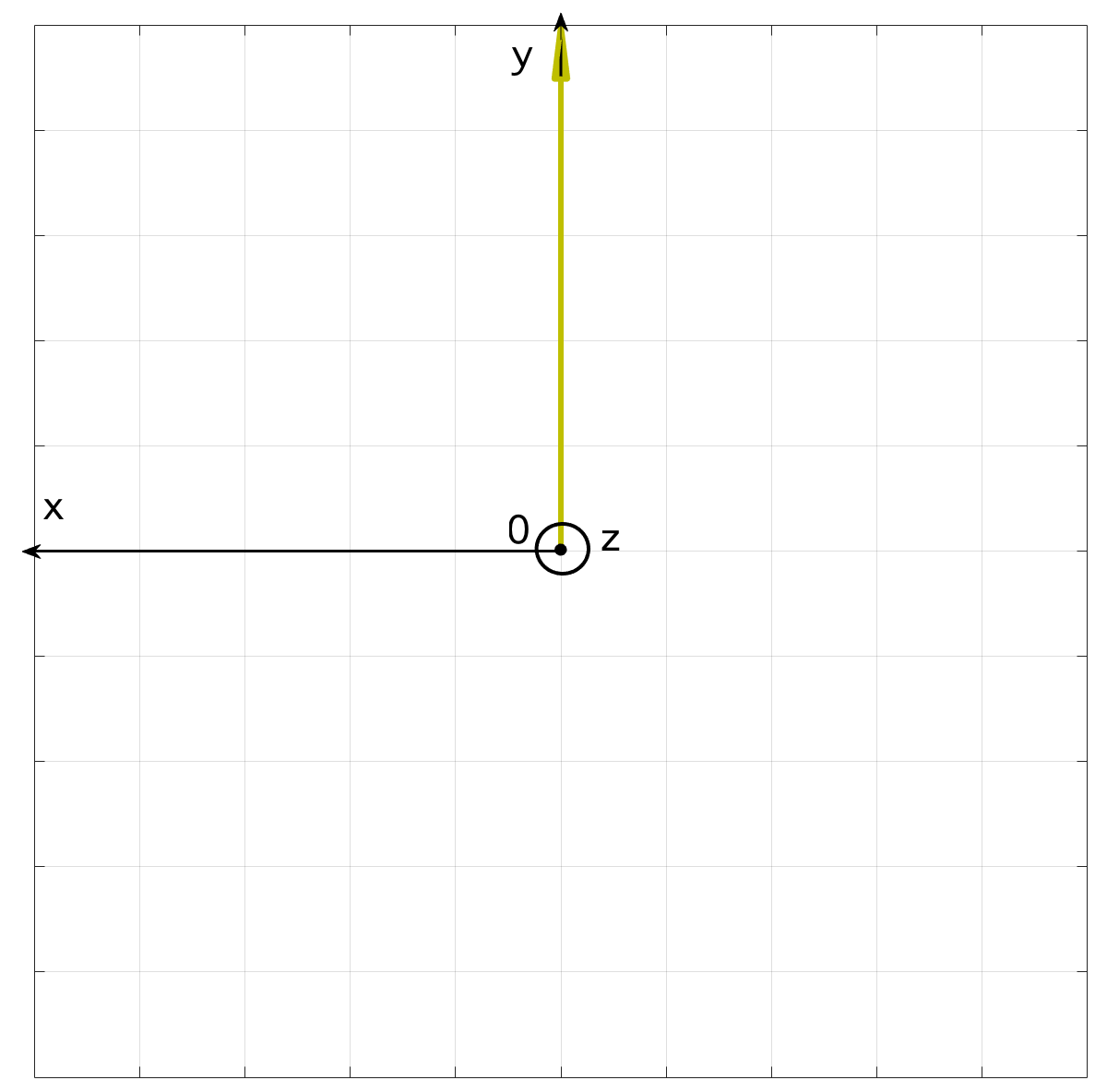
Sur la figure 3, nous représentons la propagation du champ électrique pour une onde polarisée rectilignement "verticalement".
Téléchargez l'animation au format mp4 : polarisation-3d-rectiligne.mp4 |
Téléchargez l'animation au format mp4 : polarisation-2d-rectiligne.mp4 |
3. Polarisation circulaire
La lumière peut aussi être polarisée de manière circulaire.
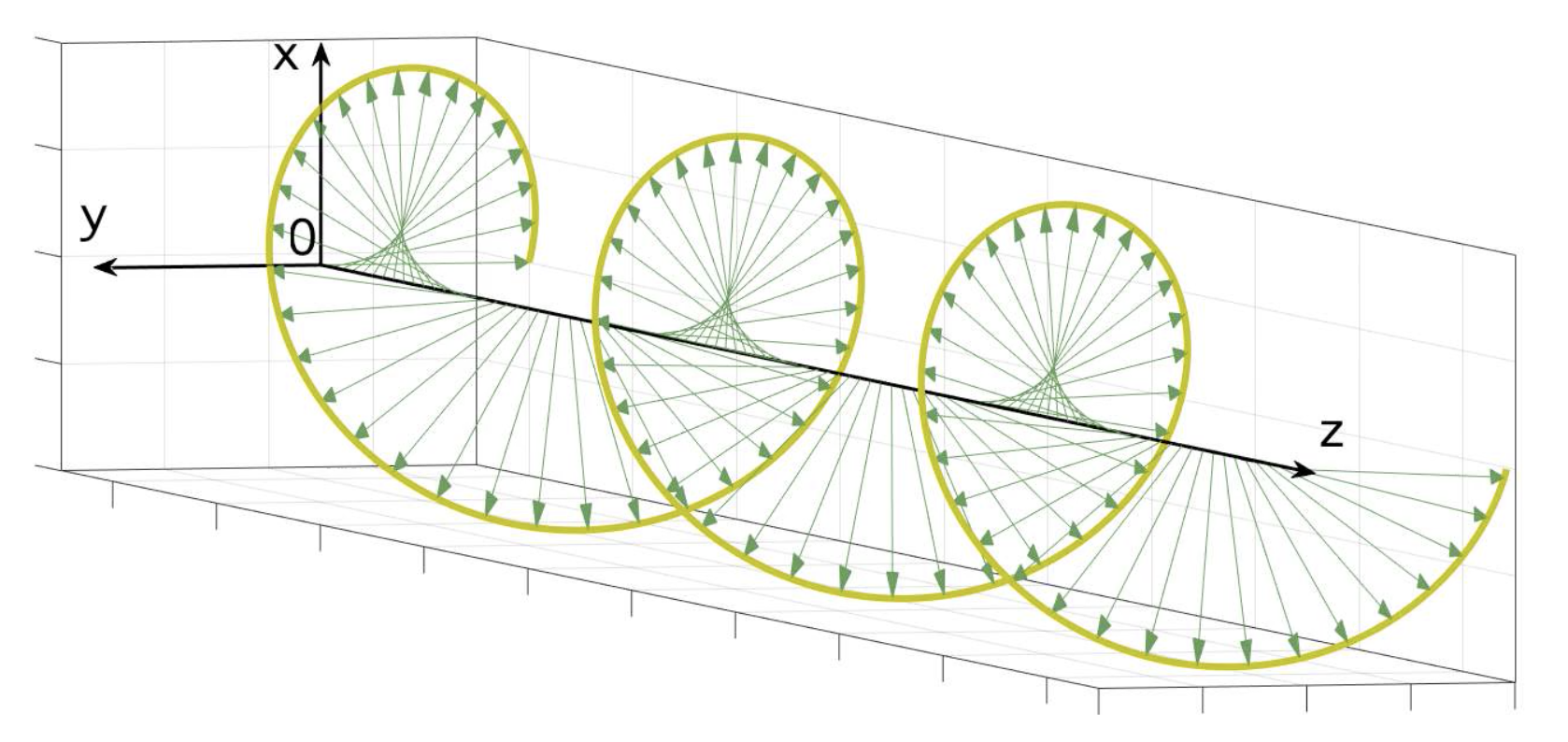
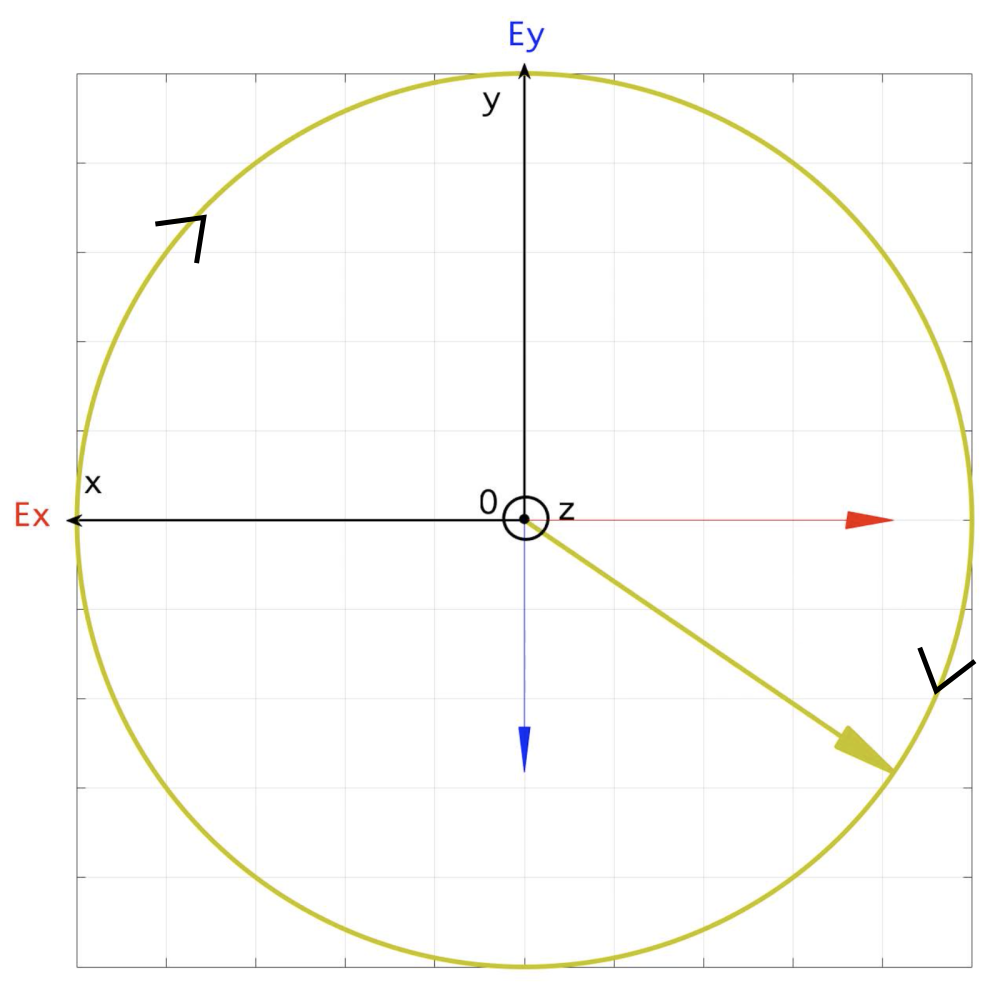
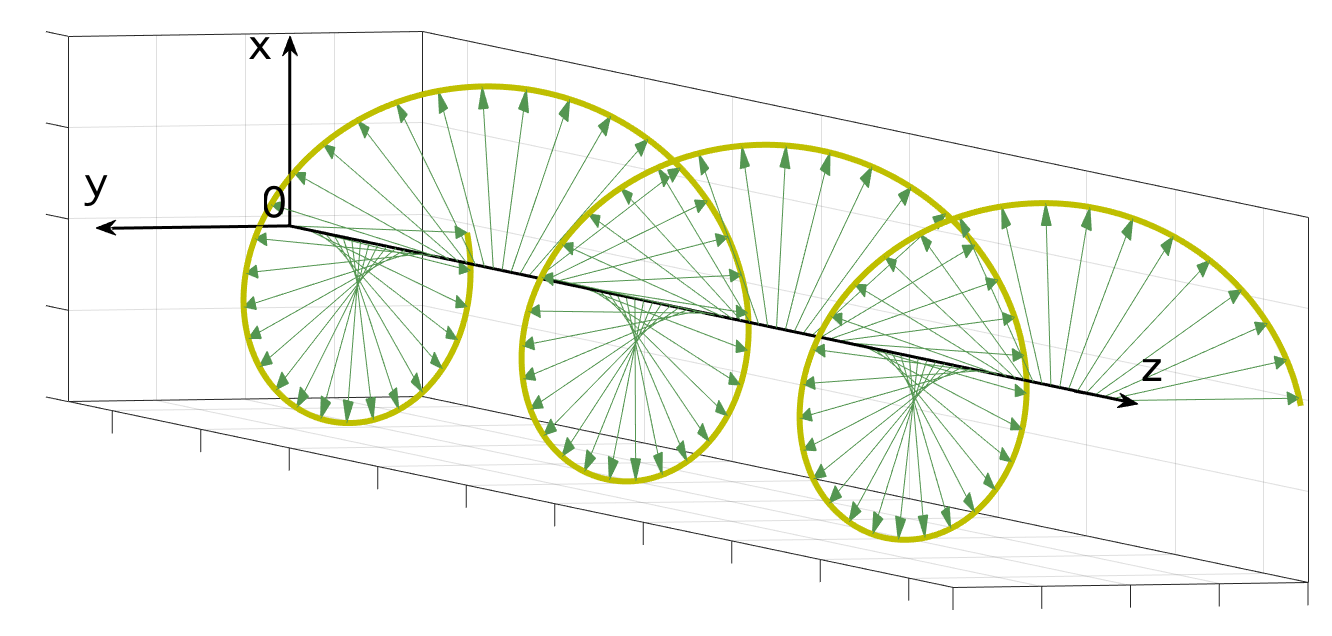
La trajectoire suivie par l’extrémité du vecteur champ électrique est une hélice d’axe la direction de propagation (Oz). Le champ électrique reste constant en module mais tourne tout en progressant, effectuant un tour complet pour chaque parcours égal à une longueur d'onde, figures 5 et 6. Si nous visualisons le vecteur champ électrique dans le plan Oxy, nous observons alors que son extrémité parcourt un cercle à vitesse angulaire constante, figures 7 et 8.
Si l’extrémité du vecteur tourne dans le sens des aiguilles d’une montre, on dit que la polarisation circulaire est droite.
Téléchargez l'animation au format mp4 : polarisation-3d-cir-d.mp4 |
Téléchargez l'animation au format mp4 : polarisation-2d-circ-d.mp4 |
Pour une polarisation circulaire droite, le vecteur champ électrique s’écrit :
$$ \overrightarrow{E(z,t)} = E_0 \cos(\omega t - k_z). \overrightarrow{u_x} - E_0 \sin(\omega t - k_z). \overrightarrow{u_y} $$
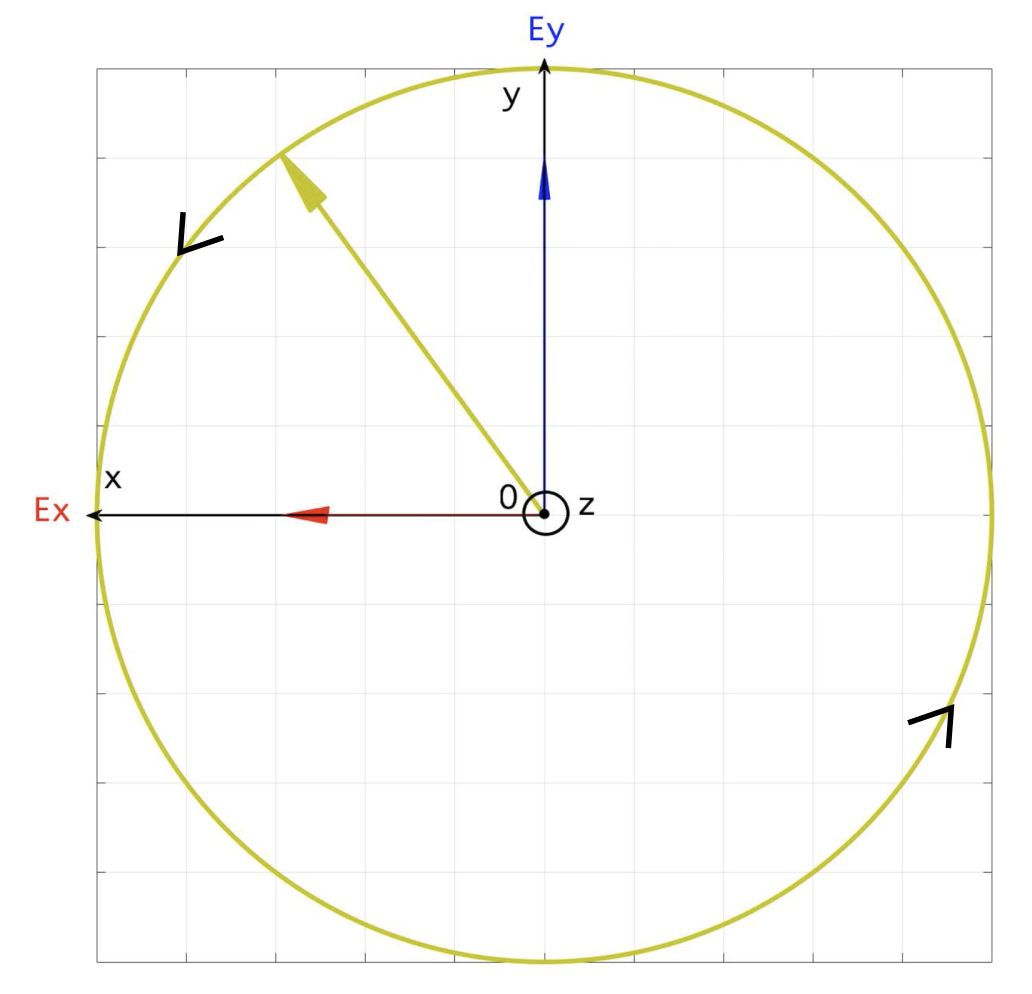
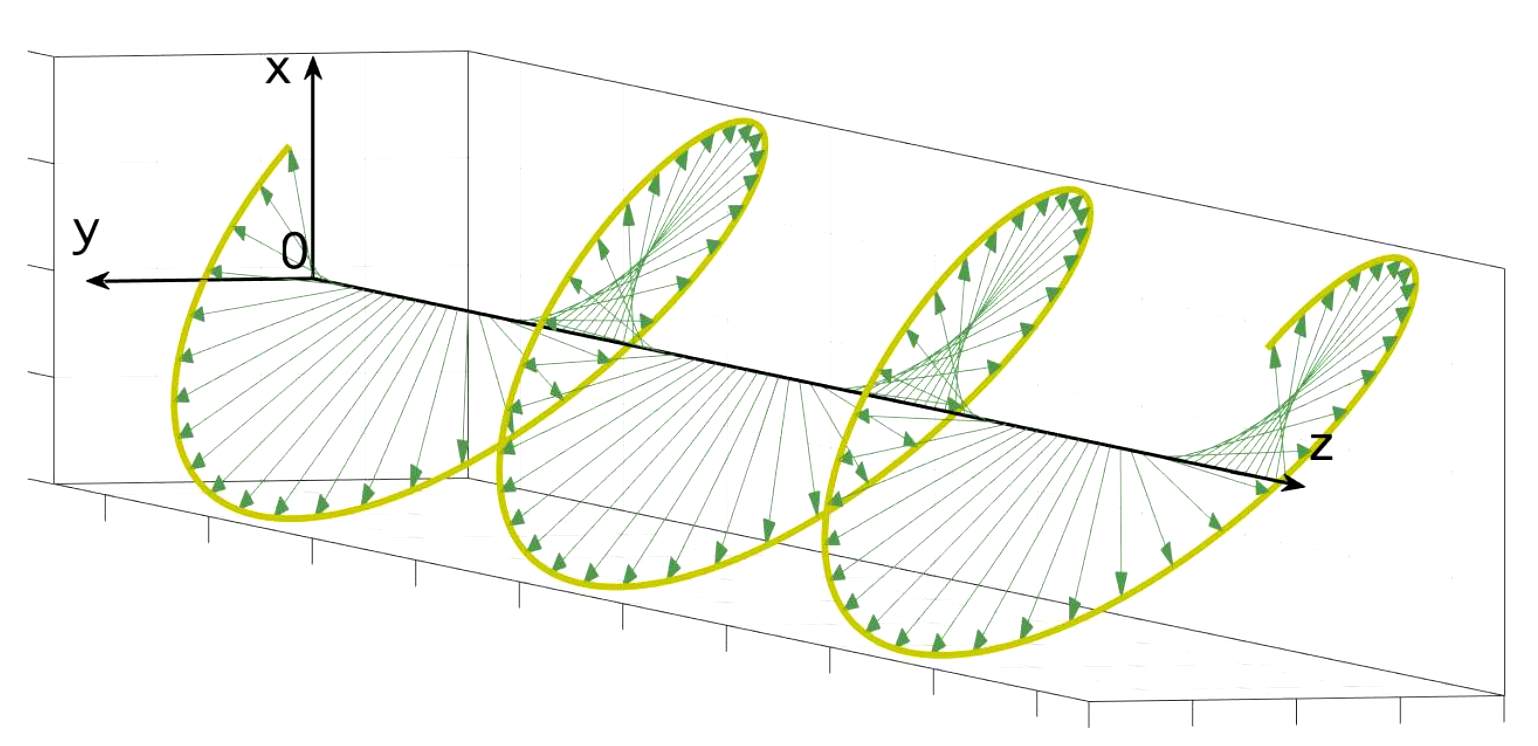
Dans le cas où l’extrémité du vecteur tourne dans le sens inverse des aiguilles d'une montre, on parle de polarisation circulaire gauche, figures 11, 12, 13 et 14.
Téléchargez l'animation au format mp4 : polarisation-3d-cir-g.mp4 |
Téléchargez l'animation au format mp4 : polarisation-2d-circ-g.mp4 |
Pour une polarisation circulaire gauche, le vecteur champ électrique s’écrit :
$$ \overrightarrow{E(z,t)} = E_0 \cos(\omega t - k_z). \overrightarrow{u_x} + E_0 \sin(\omega t - k_z). \overrightarrow{u_y} $$
4. Polarisation elliptique
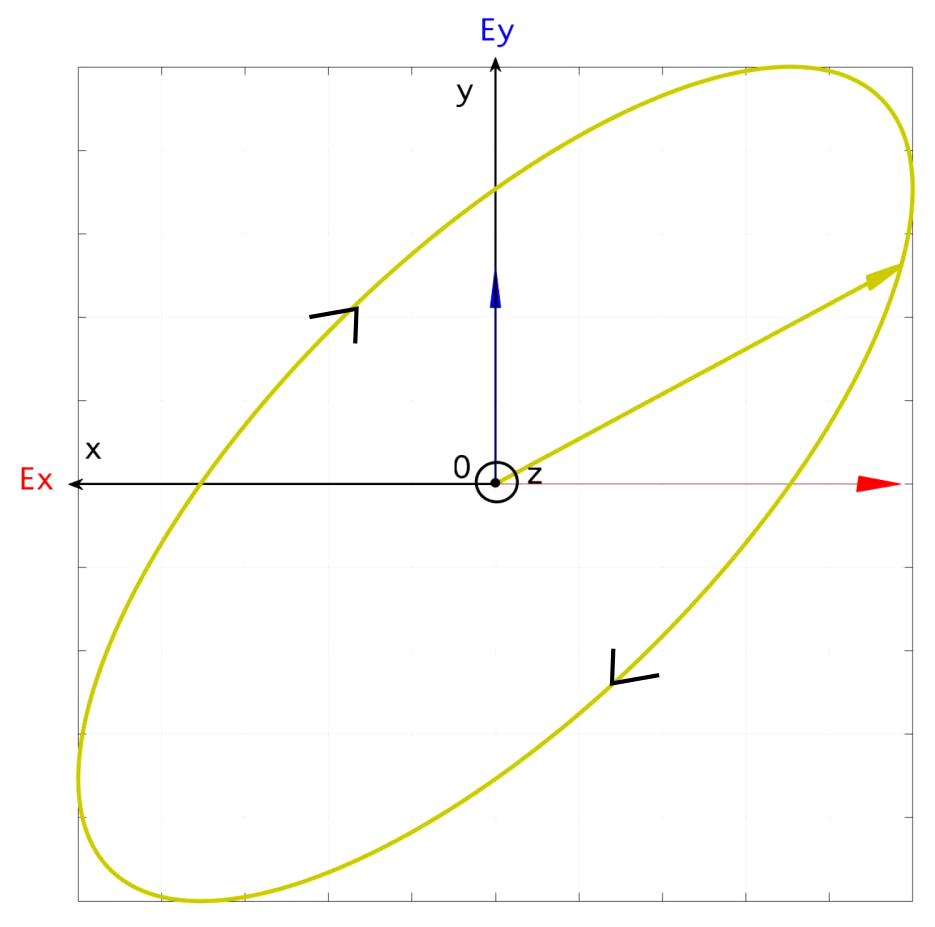
La lumière peut être aussi polarisée de manière elliptique : dans le plan (Oxy), figure 17, on voit alors l’extrémité du vecteur champ électrique parcourir une ellipse à vitesse angulaire constante.
Téléchargez l'animation au format mp4 : polarisation-3d-ellipt-d.mp4 |
Téléchargez l'animation au format mp4 : polarisation-2d-ellipt.mp4 |
Le champ électrique de l’onde possède des valeurs maximales sur les axes (Ox) et (Oy), notées E0,x et E0,y qui sont différentes et peut s’écrire :
$$ \overrightarrow{E(z,t)} = E_{0,x} \cos(\omega t - k_z). \overrightarrow{u_x} + E_{0,y} \sin(\omega t - k_z). \overrightarrow{u_y} $$
Visionner la vidéo de la physique animée sur « Polarisation de la lumière 1/3 - Qu'est-ce que la polarisation de la lumière ? ».
Pour citer cet article :
Simulations du phénomène de polarisation, décembre 2022. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/simu-polarisation.xml