Le cinéma 3D sur votre paillasse de TP - La théorie (2/2)

Dans la mesure où toute onde peut être décomposée en une superposition d’ondes planes, nous ne considérerons que celles-ci dans la suite. Pour simplifier, nous considérerons uniquement des ondes se propageant dans la direction u_z.

De manière générale, une onde plane polarisée rectilignement s’écrit simplement :

$E(z,t)=E_0\cos (\mathit{\omega t}-\mathit{kz})$

où $E_0$ est la direction de polarisation.

La plupart des sources de lumière (lampe à incandescence, fluo-compact, LED) ne possèdent pas de polarisation simple, le champ créé possède un vecteur $E_0$ d’amplitude constante mais de direction aléatoire. C’est pourquoi on les qualifie de sources polarisées aléatoirement. On peut obtenir une onde polarisée rectilignement en dirigeant cette lumière sans polarisation à travers un polariseur dichroïque.

Le polariseur dichroïque est un milieu anisotrope, ces propriétés dépendent de la direction du champ. Ce milieu va absorber le champ selon une direction particuliere tandis qu’un champ dans une direction orthogonale ne va pas être absorbé. Ainsi si une onde polarisée aléatoirement le traverse, la composante colinéaire à la direction d’absorption va disparaître et l’onde sera polarisée rectilignement dans la direction orthogonale.

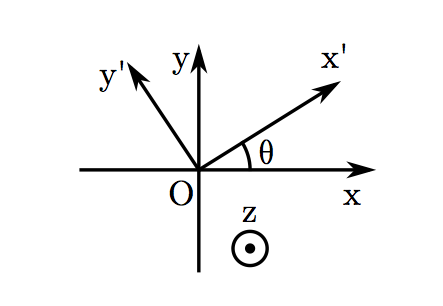
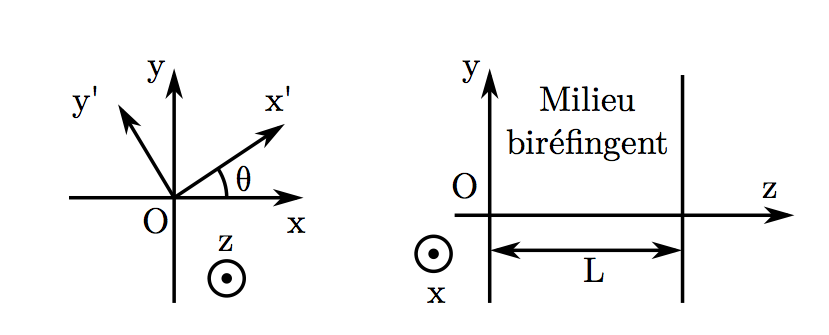
L’étude de l’impact d’un polariseur dichroïque sur une onde déjà polarisée rectilignement est riche d’intérêt. Considérons une onde incidente polarisée rectilignement selon la direction u_x et un polariseur dichroïque dont l’axe passant est selon u_x' a subit une rotation d’un angle θ. Les repères sont décrits sur la figure 1 suivante.

Source - © Romain Albert

Figure 1. Repères directs d’étude. Les deux repères ne diffèrent que par une rotation d’angle θ autour de Oz

L’onde incidente peut être écrite sur les deux repères (simple projection) :

$$ \mathbf{E}(z,t) = E_0 \mathbf{u}_x \cos \big(\omega t - kz\big) = \big(E_0 \cos \theta \mathbf{u}_{x'} + E_0 \sin \theta \mathbf{u}_{y'}\big) \cos \big(\omega t - kz\big) $$

Dans la mesure où seule la partie de l’onde selon l’axe passant traverse le système, l’onde en sortie du polariseur s’écrit :

$$ \mathbf{E}(z,t) = E_0 \cos \theta \mathbf{u}_{x'} \cos \big(\omega t - kz\big) $$

Donc si on note I₀ l’intensité de l’onde incidente, l’intensité I en sortie de l’analyseur s’écrit :

$I(\theta )\propto \langle E(t)\mathrm{.}E(t)\rangle =I_0{\cos }^2(\theta )$

où ⟨ ⟩ représente la moyenne temporelle du détecteur. L’intensité est la grandeur pertinente dans la mesure, c’est ce à quoi l’œil est sensible. Cette loi s’appelle la loi de Malus.

En partant de ce principe, on peut facilement imaginer un dispositif permettant de réaliser un effet stéréoscopique. On polarise rectilignement l’image pour l’œil droit selon u_x et l’œil gauche selon u_y (directions orthogonales) avant de les superposer sur l’écran. On donne ensuite au spectateur une lunette où le verre droit possède un polariseur passant selon u_x et un verre gauche selon u_y. L’image droite traverse le verre droit et est absorbée par le verre gauche (et vice-versa à gauche). Cette méthode permet donc bien d’envoyer une image différente sur chaque œil et ainsi d’obtenir un effet stéréoscopique.

Cette méthode a été notamment utilisée au Futuroscope de Poitiers. Malheureusement, on peut facilement voir les limites de cette méthode. Si on tourne la tête de 45°, les images droite et gauche seront mélangées sur les yeux, ce qui détruit l’effet 3d et rend l’image floue. Il faut donc garder la tête relativement droite pendant toute la séance.

Comme nous l’avions précisé dans la partie expérimentale, les sources doivent être polarisées rectilignement pour obtenir des ondes polarisées circulairement facilement. Nous allons voir quel rôle joue la polarisation dans les vidéoprojecteurs courants en expliquant rapidement leur fonctionnement. La source principale pour cette partie est la référence [8]. Il y a plusieurs techniques et de nombreuses variantes, nous nous contenterons d’en détailler deux parmi les plus courantes.

Source - © Romain Albert

Figure 2. Principe du vidéoprojecteur DLP/DMD. En variant très rapidement leur position, les micro-miroirs modifient l’intensité réfléchie par la dalle et donc l’image sur l’écran

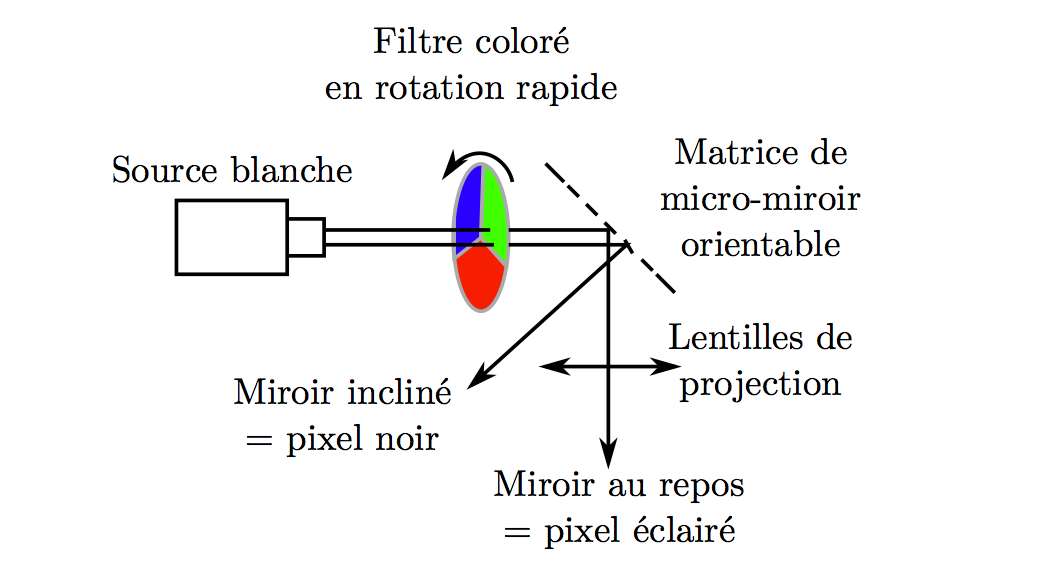
Les vidéoprojecteurs DLP/DMD sont présentés en figure 2, ils utilisent une dalle constituée de miroirs très petits (taille micrométrique) dont on peut faire varier très rapidement la position. Ainsi on peut régler l’intensité qui est renvoyée par la dalle en fonction de la position du miroir. Pour régler séparément les trois couleurs on utilise une roue chromatique. Elle est constituée de filtres de couleur primaire. En tournant, la lumière qui arrive sur la dalle a été filtrée et on constitue successivement les 3 images de couleurs différentes. Ce type de vidéoprojecteur n’est pas polarisé et un simple polariseur dichroïque permet d’obtenir la polarisation rectiligne nécessaire pour réaliser les polarisations circulaires. Il a été le premier utilisé dans les cinémas pour les projections de films numériques, un dérivé de cette technologie est employé en pratique pour les projections de films 3d.

Source - © Romain Albert

Figure 3. Principe du vidéoprojecteur tri-LCD. Ce sont ici les pixels des matrices LCD qui permettent de faire varier l’intensité

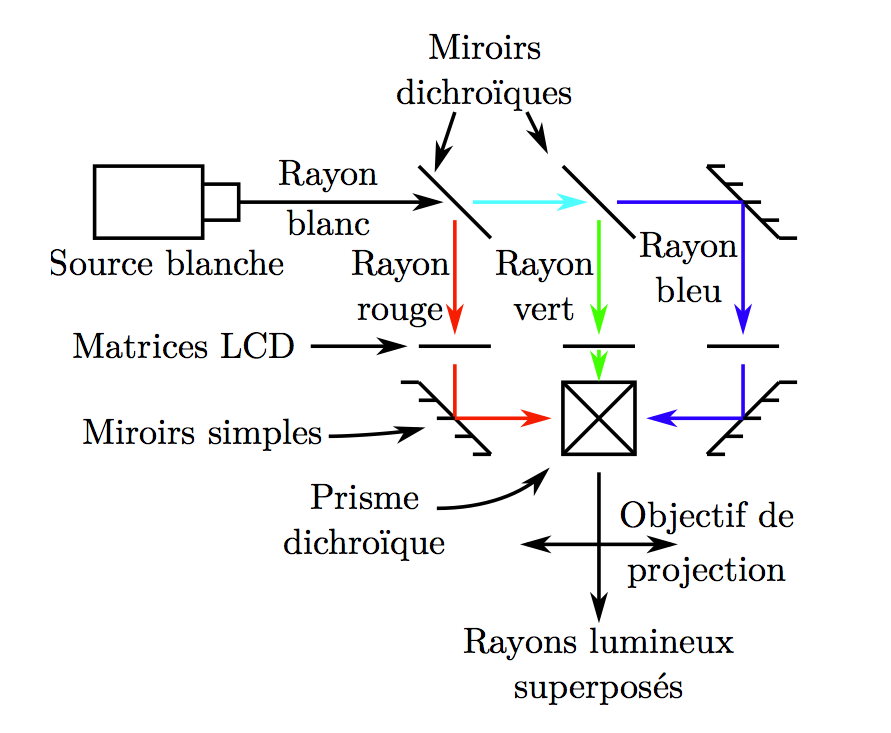
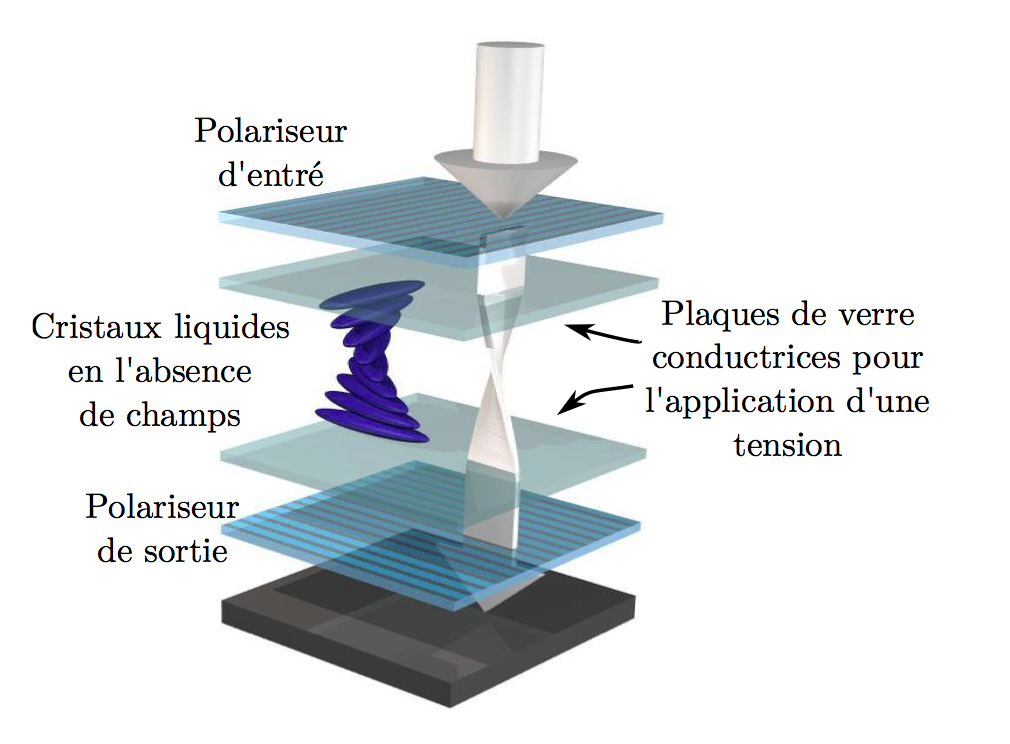
Un second type de vidéoprojecteur utilise trois dalles LCD monochromes (tri-LCD de son nom commercial), un schéma est proposé en figure 3. Les dalles sont constituées de pixel LCD dont le principe est expliqué en figure 4. Ces vidéoprojecteurs exploitent des miroirs capables de séparer des couleurs, ainsi le premier miroir va renvoyer une couleur primaire (ici le rouge) sur une première dalle LCD qui va créer une image rouge. Les deux autres couleurs traversent le miroir et sont séparées sur un deuxième miroir qui va renvoyer une couleur (ici le vert) sur une autre dalle LCD et créer la partie verte de l’image. Il ne reste plus que du bleu qui est utilisé pour constituer l’image bleu. Ensuite, ces trois images sont superposées à l’aide d’un prisme dichroïque avant d’être projetées à l’aide de lentilles.

Cette technique est intrinsèquement polarisée rectilignement à cause de la structure des pixels (figure 4). Les 3 couleurs ne possèdent en général pas la même polarisation, ce qui pose problème dans notre cas. Il peut être contourné à l’aide d’un polariseur, comme détaillé précédemment (voir Partie 2.2).

Source - © wikimedia commons

Source wikimedia commons

Figure 4. Pixel à cristaux liquides le plus simple. Il est présenté dans l’état passant, en l’absence de champ électrique entre les plaques de verre. En présence d’un champ, les cristaux s’alignent sur ce champ. La polarisation ne tourne plus, le pixel est alors non passant

Avant de comprendre comment produire des ondes polarisées circulairement, une onde polarisée circulairement s’écrit de manière générale :

$$ \mathbf{E}(z,t) = E_0 \cos \big( \omega t -kz \big) \mathbf{u}_{x} ± E_0 \sin \big( \omega t -kz \big) \mathbf{u}_{y} $$

On reconnaît alors l’équation d’un cercle dans les plans à z constant. Lorsque le signe est positif, le cercle est parcouru dans le sens trigonométrique, c’est ce que l’on appelle une onde polarisée circulairement gauche. Au contraire, si on considère le signe −, on obtient une onde polarisée circulairement droite car le cercle est parcouru dans le sens anti-trigonométrique.

Si on fait l’hypothèse que l’on peut produire et séparer les polarisations circulaires en fonction de leur chiralité (gauche ou droite), on peut facilement fabriquer un cinéma stéréoscopique. En effet il suffit de polariser circulaire gauche l’image gauche et idem pour l’image droite et de les envoyer sur l’écran. Les lunettes n’ont plus qu’à faire l’analyse des polarisations circulaires pour diriger l’image vers le bon œil. Une onde polarisée circulairement ne possédant pas d’axe privilégié, les mouvements du spectateur n’influencent pas la qualité de la perception. Naturellement, cette solution présente des inconvénients : les moyens employés pour polariser et analyser les polarisations circulaires sont plus complexes.

Pour polariser circulairement, nous allons exploiter le phénomène de biréfringence. L’objet de cet article n’étant pas de discuter de la biréfringence, nous présenterons uniquement les notions utiles à sa compréhension. Le lecteur intéressé pourra se référer à [10] qui est assez complet.

Les matériaux biréfringents sont des matériaux diélectriques qui ne présentent pas les mêmes propriétés optiques dans toutes les directions. Dans la suite, on considère un milieu biréfringent uniaxe où deux axes propres d’indices différents font partie du plan Oxy, orthogonal à la direction de propagation (Oz) des ondes planes. On considère que l’axe rapide est la direction u_x' avec un indice n_x' et l’axe lent est selon la direction u_y' avec un indice n_y'. L’axe rapide possède un indice optique plus petit que l’axe lent : n_x' plus petit que n_y'.. Pour clarifier ces notations et le système étudié, voir la figure 5.

Source - © Romain Albert

Figure 5. Représentation du système étudié, θ représente comme précédemment la rotation des systèmes d’axe du champ et du milieu biréfringent (de longueur L)

On éclaire ce milieu avec une onde polarisée linéairement selon u_x : $E_0=E_0{u}_x$ Par ailleurs on fixe la phase de l’onde à zéro sur la face d’entrée du milieu biréfringent. Le champ à l’entrée du milieu peut donc s’écrire dans le repère (u_x', u_y') lié au milieu :

$$ \mathbf{E}(z,t) = \big( E_0 \cos \theta \mathbf{u}_{x'} + E_0 \sin \theta \mathbf{u}_{y'} \big) \cos \big( \omega t -kz \big) $$

Calculons le champ en sortie du milieu biréfringent. On considérera que la transmission aux interfaces est parfaite. Par ailleurs, l’indice optique étant différent en fonction l’axe, le nombre d’onde est différent : $k_{x\text{'}}=\frac{2\pi n_{x\text{'}}}{\lambda }$ et $k_{y\text{'}}=\frac{2\pi n_{y\text{'}}}{\lambda }$ On obtient alors le champ sur la face de sortie :

$$ \mathbf{E} \big(z=L,t\big ) = E_0 \cos \theta \mathbf{u}_{x'} \cos \big( \omega t -\frac{2 \pi}{\lambda} n_{x'} L \big) + E_0 \sin \theta \mathbf{u}_{y'} \cos \big( \omega t - \frac{2 \pi}{\lambda} n_{y'} L \big) $$

En redéfinissant l’origine des phases, on obtient :

$$ \mathbf{E} \big(z=L,t\big ) = E_0 \cos \theta \mathbf{u}_{x'} \cos \big( \omega t \big) + E_0 \sin \theta \mathbf{u}_{y'} \cos \big( \omega t - \frac{2 \pi}{\lambda} (\Delta n) ~L \big) $$

$\Delta n=n_{y\text{'}}-n_{x\text{'}}$

Donc pour obtenir une onde polarisée circulairement, il faut que :

$\frac{2\pi }{\lambda }(\Delta n)L=\phi =\frac{\pi }{2}+p\pi$

où p est un entier.

De plus il faut que l’amplitude sur les deux axes soit identique : θ= ±π/4. On obtient alors une onde polarisée circulairement droite ou gauche en fonction du signe de θ et de la valeur de l’entier p. Ce type de lame est appelé une lame quart d’onde, en effet, un déphasage de π/2 correspond directement à un retard d’un quart de longueur d’onde.

Cependant, comme on peut le voir dans la dernière équation, le critère d’accord dépend de la longueur d’onde. Une lame quart d’onde ne peut pas avoir un retard de π/2 pour l’ensemble du spectre visible. La qualité de la polarisation circulaire dépendra donc de la longueur d’onde. Dans le cas présent, nous utilisons une lame quart d’onde ajustée dans le vert car c’est le maximum de sensibilité de l’œil. Le violet et le rouge ne seront pas parfaitement filtrés par l’analyseur (constitué simplement d’une lame quart d’onde puis d’un polariseur), ce qui n’est pas très grave car l’œil y est beaucoup moins sensible.