Historique : de Galilée à nos jours, évolution de la notion de vitesse de la lumière

On a longtemps cru que la lumière se propageait instantanément. Dans ce cas, nul besoin de mesurer sa vitesse ! On n'a d'ailleurs alors qu'une compréhension très limitée de la nature de la lumière : sont-ce, comme on se le demande dans l'Antiquité, des particules qui partent de l'objet regardé, de l'oeil de l'observateur ou des deux ? La lumière serait-elle plutôt, comme on l'a affirmé pour la première fois vers le XIII^ième siècle, une onde ? La lumière peut-elle se propager dans le vide ?

Galilée, au début du XVII^ième siècle, fut un des premiers à penser que la lumière se propageait à vitesse finie. Il a tenté de mesurer cette vitesse en plaçant deux personnes éloignées de quelques kilomètres et munies d'horloges. Le temps mis par la lumière pour parcourir cette distance est de l'ordre de 10^-5s seulement, durée impossible à mesurer à l'époque, son expérience n'a donc pas été concluante.

Depuis Galilée, des mesures de plus en plus précises ont été effectuées. En 1983, cependant, le point de vue a changé : au lieu de définir précisément le mètre et la seconde et de mesurer la vitesse de la lumière en utilisant ces définitions, la valeur de la vitesse de la lumière dans le vide est désormais fixée par convention. Elle vaut, par définition, c = 299.792.458 m.s^-1. Cette donnée, ajoutée à la définition actuelle de la seconde, sert à définir le mètre.

En fait, cette définition qui peut paraître simple à première vue n'est possible que parce que certaines conditions, qui n'étaient pas évidentes un siècle auparavant, sont remplies.

Un étalon de mesure (de temps, de longueur, de masse, etc...) n'est convenable que s'il est invariant dans le temps, indépendant de l'observateur, et suffisamment facile à utiliser. Le "pas" d'un être humain est un exemple de mauvais étalon de mesure de longueurs puisque, bien qu'il soit facile de mesurer une longueur donnée avec cet étalon, la longueur d'un "pas" varie fortement suivant l'observateur. Un mouvement insuffisamment périodique (comme le jour solaire vrai qui varie beaucoup au cours de l'année) constitue là aussi un mauvais étalon de mesure... On sait aujourd'hui que la vitesse de la lumière dans le vide a l'avantage de constituer, d'après la théorie de la relativité, une valeur absolument fixe, universelle et indépendante de l'observateur, ce qui en fait un bon choix d'étalon de mesure.

Une chronologie rapide de l'évolution des définitions de la seconde et du mètre, ainsi que de notre connaissance de la vitesse de la lumière, permet de mieux comprendre comment on en est arrivé à utiliser la vitesse de la lumière comme étalon de longueur :

La vitesse de la lumière : 1676

Après la tentative infructueuse de Galilée, Olaüs Römer détermine pour la première fois un ordre de grandeur de la vitesse de la lumière en étudiant l'avance ou le retard apparent dans le mouvement des satellites de Jupiter (il étudie plus précisément l'intervalle entre deux occultations des satellites derrière la planète). Il constate que ce décalage par rapport à la théorie dépend de la distance que la lumière doit parcourir pour aller de la Terre à Jupiter. Il en déduit une première approximation de la vitesse de la lumière.

Explication :

Gabrielle Bonnet

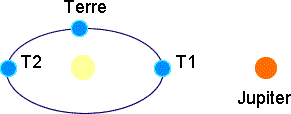
Dans la position T₁, la Terre est sur le point de son orbite le plus proche de Jupiter. Dans la position T₂, la Terre est dans sa position la plus éloignée de Jupiter. La lumière met 1000 s soit à peu près 17 minutes de plus pour arriver à T₂, en provenance du voisinage de Jupiter, que pour arriver à T₁. Cette constatation permet, connaissant la distance qui nous sépare du Soleil, de déterminer un ordre de grandeur de la vitesse de la lumière (3 × 10⁸ m.s^-1 = 2 × 1,5 × 10¹¹ m/ 1000 s ).

Le mètre : 1795

Première tentative pour unifier les unités de mesure de longueurs : les révolutionnaires français décident de choisir une unité de longueur qui soit parfaitement universelle, sans "rien d'arbitraire ni de particulier à la situation d'un peuple sur le globe". Les dimensions de la Terre obéissent à ces conditions : elles ne sont pas plus françaises qu'anglaises ou chinoises. Le mètre est ainsi défini comme la 1/40.000.000^ième partie du méridien terrestre. Cette valeur n'est toutefois pas totalement indépendante du méridien considéré... pour plus de précision, le mètre est alors défini comme la dix millionième partie du quart Nord du méridien de Paris

Par définition, le méridien terrestre est donc un nombre entier (4 × 10⁷) de mètres! La définition actuelle du mètre est proche de la définition de l'époque, en effet, un méridien terrestre fait à peu près 2 π × 6,37 × 10⁶ m = 4,00 × 10⁷ m si on garde 3 chiffres significatifs.

La seconde : début du dix-neuvième siècle

La seconde est définie comme la 1/86.400^ième partie du jour solaire moyen. On doit définir la seconde à partir d'une valeur moyenne car le jour solaire véritable (temps séparant deux passages successifs du soleil au méridien du lieu considéré) varie selon la période de l'année à laquelle on se trouve, essentiellement du fait de l'ellipticité de la trajectoire de la Terre. On sait qu'une orbite elliptique n'est pas parcourue à vitesse constante, la Terre se déplace ainsi plus vite lorsqu'elle est près du Soleil que lorqu'elle en est éloignée. Cette irrégularité de la vitesse de la Terre a une influence sur la durée du jour solaire qui varie donc dans le courant de l'année : il est compris entre 23 h 59 min 39 s et 24 h 0 min 30 s. Si on fait la moyenne sur l'année, c'est-à-dire sur la totalité de l'orbite terrestre, cependant, on obtient le jour solaire moyen, qui, dans l'idéal d'un mouvement terrestre parfaitement périodique d'une année sur l'autre, devrait être constant.

À cet étalon de durée est associé un « temps », le « Temps Universel » (T.U.) qui correspond au temps solaire moyen du méridien de Greenwich augmenté de 12 h (à « midi solaire moyen », le temps solaire moyen est 0).

La vitesse de la lumière : 1848 à 1878

D'importantes avancées sont réalisées dans la connaissance de la vitesse de la lumière. En 1849, H. Fizeau améliore la mesure de la vitesse de la lumière à l'aide d'une roue dentée occultant périodiquement la lumière (cette mesure est en fait une mesure de la vitesse de la lumière dans l'air), L. Foucault, en 1850, invente un dispositif de miroirs (l'un d'entre eux tourne à grande vitesse : 300 tours/seconde) et mesure grâce à celui-ci la vitesse de la lumière dans l'eau, et en 1878, Michelson et Morley réalisent une mesure de la vitesse de la lumière précise à 50 km/h près.

H. Fizeau

L. Foucault

A. Michelson

Pour en savoir plus sur l'expérience de Fizeau :

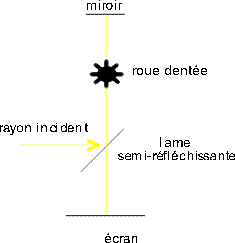
Fizeau a envoyé de la lumière entre Suresnes et Montmartre. Cette lumière passe à travers une roue dentée en mouvement, parcourt la distance Suresnes-Montmartre, est réfléchie par un miroir, et revient sur la roue dentée pour arriver, si elle n'est pas occultée par une dent, sur un écran. Pour certaines vitesses de rotation de la roue, rien n'arrive sur l'écran, car la lumière est soit occultée au départ par une dent, soit occultée lors de son deuxième passage à travers la roue. Connaissant la vitesse de rotation de la roue, l'intervalle entre deux dents, et la distance parcourue par la lumière, on peut en déduire une bonne approximation de la vitesse de la lumière. L'expérience de Fizeau présentée au Musée virtuel de l'Ecole Polytechnique.

L'expérience de Foucault :

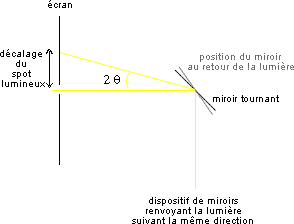
Un dispositif de miroirs permet à une source d'envoyer de la lumière qui revient à son point de départ, si tous les miroirs sont fixes, après avoir parcouru une distance de 20 m. Si un des miroirs est maintenant mis en rotation, la lumière est légèrement décalée à son retour vers la source. Ce décalage est proportionnel à l'angle dont a tourné le miroir pendant le temps que met la lumière à parcourir son trajet dans le dispositif. Avec un miroir tournant à une vitesse de plusieurs centaines de tour par seconde, on peut obtenir un décalage mesurable et en déduire la vitesse de la lumière. L'expérience de Foucault présentée au Musée virtuel de l'Ecole Polytechnique.

Le mètre : 1889

La longueur du mètre est désormais celle du mètre étalon déposé au Bureau des Poids et Mesures à Sèvres.

La seconde : 1956

Le jour solaire moyen n'est pas tout à fait constant car le mouvement de la Terre n'est pas parfaitement périodique. Il y a des écarts de 1 à 2 s par an. De plus, la Terre, freinée par les marées, voit la durée d'un jour solaire moyen augmenter légèrement au fil des années (de 1,64 × 10^-5 s/an ). On propose donc une définition de la seconde plus rigoureuse : la seconde sera définie comme 1/31.556.925,9747^ième de la durée de l'année tropique (durée séparant deux équinoxes de printemps successives) 1900. Le temps correspondant est le « Temps des Ephémérides » (T.E.).

Le mètre : 1960

Les transitions atomiques sont de bons candidats pour fournir de meilleures définitions des unités fondamentales. Elles donnent des valeurs plus précises que celles fondées sur les dimensions ou les mouvements de la Terre. Le mètre est défini comme 1.650.763,63 fois la longueur d'onde dans le vide de la radiation qui correspond à la transition entre les niveaux 2p10 et 5d5 de l'isotope 86 du Krypton.

La seconde : 1967

C'est au tour de la seconde d'être définie à partir des transitions atomiques : la fréquence de transition entre les 2 niveaux hyperfins de l'état fondamental de l'atome de Cesium 133 est, par définition, F = 9.192.631.770 Hz. Cette définition a une exactitude de 2 × 10^-14 soit un décalage d'une seconde tous les 1.500.000 ans !

Cette nouvelle définition de la seconde définit un nouveau temps, le « Temps Atomique International » (T.A.I.). Un compromis a été trouvé avec le « Temps Universel », c'est le « Temps Universel Coordonné » (U.T.C. pour l'abbréviation anglaise) qui utilise la seconde du T.A.I. et ajoute ou retranche le cas échéant une seconde à l'année le 31 décembre à 24 heures ou le 30 juin à 24 heures, de façon à ce qu'en valeur absolue, l'écart entre le Temps Universel et le Temps Universel Coordonné soit toujours inférieur à 0,9 s.

La vitesse de la lumière et le mètre : 1983

Dernière définition du mètre : elle fait intervenir la vitesse de la lumière. Par définition, on a fixé la vitesse de la lumière dans le vide à c = 299.792.458 m.s^-1. Suivant cette définition, la donnée de la seconde suffit à définir le mètre. Cette vitesse est un étalon de mesure idéal. En effet, contrairement à certains des étalons choisis précédemment (comme le jour solaire moyen), c est rigoureusement constante et elle est indépendante de l'observateur considéré (qu'il soit au repos ou en mouvement).

Cette « course à la précision » est-elle utile, et à qui ? A-t'elle des applications dans la vie courante ? Pourquoi définir la seconde avec une exactitude de 2 × 10^-14 plutôt que de "seulement" 10^-7, par exemple ?

En fait, un grand nombre d'instruments utilisent des mesures de durée pour déterminer des distances (via la valeur de la vitesse de la lumière) : le télémètre laser, le GPS, etc... Dans un grand nombre de ces applications, une grande précision sur la valeur de la seconde est cruciale : supposons que l'on fasse une erreur de 10^-7 secondes sur la mesure du temps, par exemple, comme la vitesse de la lumière est c = 299.792.458 m.s^-1, cette incertitude sur la mesure du temps correspond à une erreur sur les distances de 30 mètres environ. Cette erreur est inadmissible si on souhaite, par exemple, téléguider un avion pour qu'il sorte d'un hangar !

Dans le vide...

La lumière, dans le vide, a la même vitesse : c = 299.792.458 m/s qu'elle soit perçue par un objet immobile ou par un objet en mouvement. C'est un des points apparemment paradoxaux de la théorie de la relativité. Cette invariance de la vitesse de la lumière dans le vide en fait un étalon universel idéal pour définir le mètre. Pour en savoir plus sur les paradoxes apparents de la théorie de la relativité, voir l'article « Relativité et vitesse de la lumière » du dossier « La vitesse de la lumière ».

Dans un milieu matériel...

Dans un milieu matériel, la lumière se déplace plus lentement que dans le vide. La vitesse v de la lumière dans un milieu d'indice n est v = c / n. L'indice n de la plupart des matériaux est assez faible : 1,0003 pour l'air, 1,33 pour l'eau et à peu près 1,5 pour le verre. Cet indice dépend en fait de la longueur d'onde considérée : c'est ainsi que les différentes longueurs d'onde (associées chacune à une couleur si on est dans le domaine du visible) d'un faisceau de lumière polychromatique se comportent différemment à l'intérieur d'un milieu matériel. Sous certaines conditions, ces longueurs d'onde peuvent être séparées : c'est le phénomène de dispersion, responsable de l'existence des arcs-en-ciel ainsi que de celle des spectres.

Deux conséquences de la dispersion : les arcs-en-ciel et les spectres

Vous pouvez voir des explications complètes sur l'origine de l'indice dans l'article « Indices optiques : dérivation à partir des équations de Maxwell, signification physique, expression » de ce dossier : « La vitesse de la lumière ».

Réussir à stopper la lumière...

La plupart des indices connus sont assez proches de 1 : un des indices les plus importants recontrés "dans la vie courante" est celui du diamant qui vaut 2,42. Cependant, récemment, une équipe de chercheurs menée par Mme Lene Hau a réussi a ralentir la lumière de façon remarquable, en la faisant passer à travers un condensat de Bose-Einstein quasiment à la température du zéro absolu. Après une vitesse d'une soixantaine de km/h en 1999, ils ont atteint 1,5 km/h en mars 2000 (soit 50 cm/s), puis ont réussi, en 2001 à "arrêter" la lumière (Lien vers les pages du groupe de recherche de Lene Hau à l'université d'Harvard (en anglais))

... Et aller plus vite que la lumière

Alors que la théorie de la relativité affirme qu'aucun objet ne peut dépasser c (vitesse de la lumière dans le vide), il est possible de dépasser la vitesse de la lumière, pourvu que celle-ci se déplace dans un milieu d'indice supérieur à 1. Lorsqu'un objet "dépasse le mur de la lumière" on constate des phénomènes analogues à ce qui se produit lorsqu'un avion dépasse le "mur du son" : ces phénomènes sont connus sous le nom d'effet Cherenkov. Lire l'article « Plus vite que la lumière ? » du dossier « La vitesse de la lumière ».

Article suivant : « Indices optiques : dérivation à partir des équations de Maxwell, signification physique, expression ».

Dossier : « La vitesse de la lumière ».