Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Quelle est la forme de la trajectoire de la Lune dans le référentiel héliocentrique ?
07/12/2015
Résumé
Nous proposons dans cet article d'avoir une idée de la forme de la trajectoire de la Lune dans le référentiel héliocentrique.
Table des matières
Pour des raisons pratiques de lisibilité, on représente souvent les positions des planètes dans le système solaire sans respecter les échelles. Les schémas ou simulations ainsi obtenus pourraient laisser croire, comme dans le cas de la représentation du mouvement rétrograde de Mars, que la Lune pourrait aussi avoir un mouvement rétrograde dans le référentiel du soleil. Dans cet article nous montrons qu'un simple calcul d'ordre de grandeur permet de se rendre compte que ce n'est pas le cas et que sa trajectoire autour du soleil est très proche de celle de la Terre.
Calcul de la vitesse de la Lune par rapport au Soleil
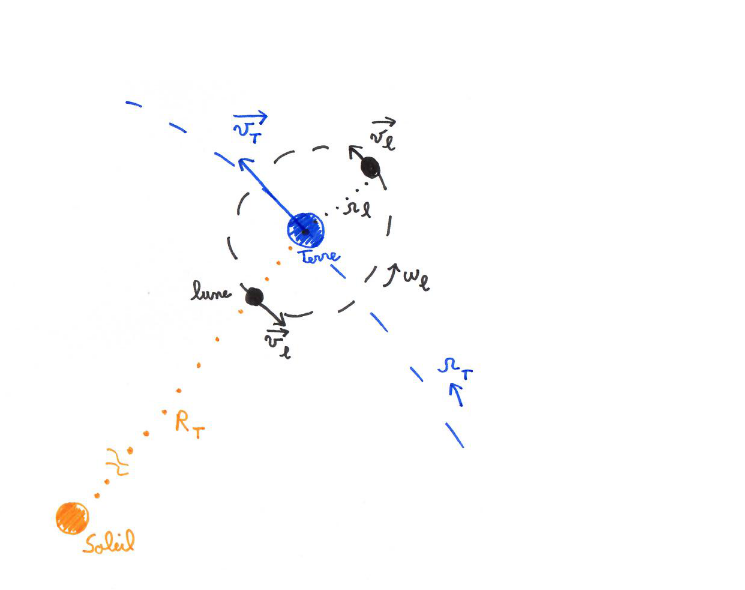
Sur la figure 1, nous avons représenté le Soleil, une partie d'orbite de la Terre et l'orbite de la Lune autour de la Terre. Pour une meilleure visibilité, les échelles ne sont pas respectées.
La Terre se trouve à la distance RT du Soleil et tourne autour de lui à la vitesse angulaire ΩT = 2pi/TT, avec TT ≈ 365 jours. La Lune se trouve à la distance rl de la Terre et tourne autour d'elle à la vitesse angulaire ωl = 2pi/Tl, avec Tl ≈ 28 jours.
La vitesse de la Terre dans le référentiel du Soleil est vTerre/Sol = RT ΩT
La vitesse de la Lune dans le référentiel de la Terre est vlune/Terre = rl ωl
Une simple comparaison des rayons des orbites et des vitesses de révolution permet d'estimer la vitesse de la Lune par rapport au Soleil.
- Comme les excentricités sont petites, on peut estimer que les orbites de la Terre autour du Soleil et de la Lune autour de la Terre sont circulaires. Le rayon de l'orbite de la Terre est RT ≈ 150.109m et celui de la Lune est rl ≈ 400.106m. Le rayon de l'orbite de la Terre est alors environ 400 fois plus grand que le rayon de l'orbite de la Lune, d'où RT ≈ 400 x rl
- la Terre effectue une révolution autour du Soleil en 365 jours et la Lune effectue une révolution autour de la Terre en 28 jours, donc une période 13 fois plus petite, ωl ≈ 13 x ΩT.
Ainsi, vTerre/Sol ≈ 400/13 x vlune/Terre ≈ 30 x vlune/Terre
Ce calcul simple permet de mettre en évidence que la vitesse de la Terre par rapport au Soleil est environ 30 fois plus grande que la vitesse de la Lune par rapport à la Terre. Donc la vitesse de la Lune par rapport au Soleil varie entre 103% et 97% de la vitesse de la Terre par rapport au Soleil. En particulier, comme la vitesse de la Lune autour du Soleil n'est jamais négative, il n'y a pas de mouvement de rétrogradation de la Lune dans le référentiel du Soleil.
Représentation de la forme de la trajectoire
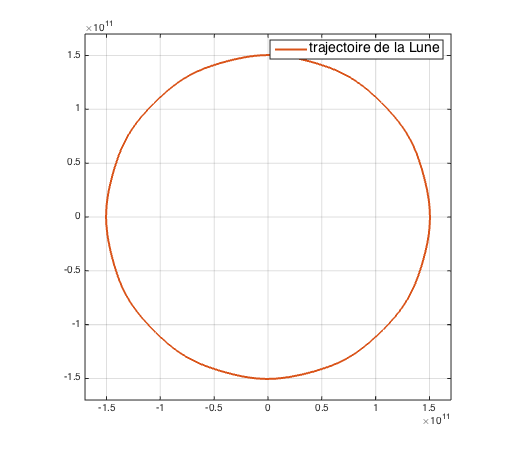
Nous avons tracé ci-dessous la forme de la trajectoire de la Lune vue dans le référentiel héliocentrique. Nous faisons les hypothèses que les orbites de la Terre autour du Soleil et de la Lune autour de la Terre sont circulaires. La figure 2 présente la trajectoire de la Lune autour du Soleil.
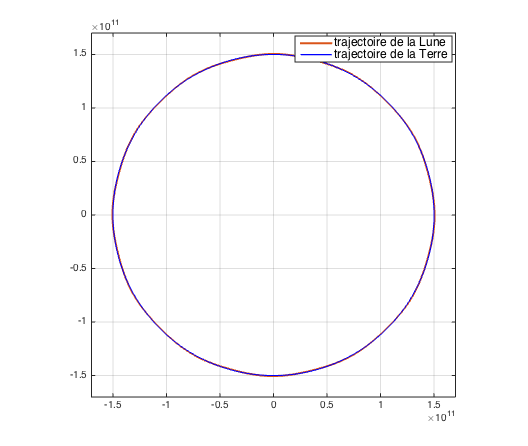
Sur la figure 3, on superpose la trajectoire de la Terre à celle de la Lune. Il est difficile de les différencier.
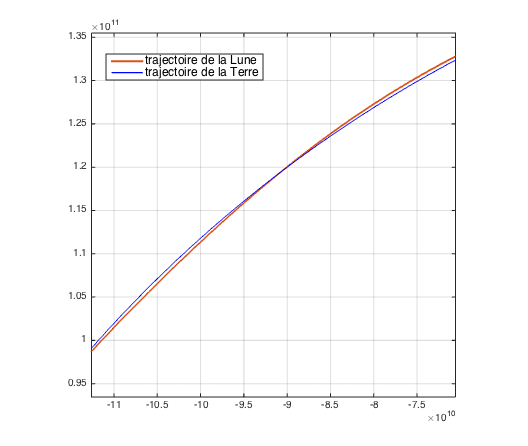
A l'aide d'un zoom, nous observons sur la figure 4, le tout petit écart entre la trajectoire de la Lune et celle de la Terre vu par rapport au Soleil.
Visualisation avec le logiciel Stellarium
Nous proposons maintenant de visualiser les orbites de la Terre et de la Lune dans le référenteil héliocentrique à l'aide du logiciel Stellarium.
L'orbite de la Terre est représentée en rouge, celle de la Lune en jaune, les images sont incrémentées tous les cinq jours. Le pointeur « vise » la Terre et la place au centre de l'écran. La Lune n'est pas représentée par un point mais son orbite autour de la Terre est représentée par un cercle jaune.
Simulation réalisée avec Stellarium.
Pour citer cet article :
Quelle est la forme de la trajectoire de la Lune dans le référentiel héliocentrique ?, Chareyron, décembre 2015. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/orbite-lune-referentiel-soleil.xml