Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Le système International d'unités
21/04/2014
Résumé
Cet article présente le Système International d'unités (historique, création d'unités dérivées, et récentes re-définitions d'unités de base), il est tiré de la conférence de Nicolas Feltin donnée le 19 février 2014 pour le Département de Physique de l'ENS de Lyon.
Table des matières
Introduction
Le constat de la situation en matière d'unités, à la veille de la révolution française, est bien décrit par le texte ci-dessous, de Denis Guedj, tiré de La Méridienne, 1792-1799, p 9-10.
« Le bois se vendait à la corde; le charbon de bois à la tonne; le charbon de terre à la bacherelle; l'ocre au tonneau, et le bois de charpente à la marque ou à la solive. On vendait les fruits à cidre à la poiçonnée; le sel au muid, au sétier, à la mine, au minot, au boisseau et à la mesurette; la chaux se vendait au poinçon, et le minerai à la razière. On achetait l'avoine au picotin et le plâtre au sac; on se procurait le vin à la pinte, à la chopine, à la camuse, à la roquille, au petit pot et à la demoiselle... Les longueurs étaient mesurées en toise et en pied du Pérou, lequel équivalait à un pouce, une logne et huit points du pied du roi - pied du roi qui se trouvait être celui du roi Philictère, celui de Macédoine et celui de Pologne... À Marseille, la canne pour les draps était plus longue que celle pour la sopie d'environ un quatorzième. Quelle confusion ! 7 à 800 noms... »
Il existait donc un nombre conséquent d'unités, dont certaines absurdes, et pour simplifier la situation, il a été a demandé à Condorcet, en 1791, de s'atteler au problème de l'unification des poids et mesures.
Ce n'est qu'en 1799 qu'un système métrique cohérent a été mis en place en France. Dans l'intervalle de temps l'idée des personnalités (Condorcet, Borda, Laplace, Lagrange et Monge) en charge de ce projet était de construire un système international d'unités. Les tensions entre La France et l'Angleterre ont fait que l'Angleterre a refusé de s'impliquer dans ce système international. C'est seulement en 1875 que la signature de la convention a permis d'avoir enfin un système international d'unités.
Une première définition du mètre est donnée en 1799 et restera valide jusqu'en 1983. Le mètre étant alors défini comme la dix-millionième partie de la distance entre l'équateur et le pôle mesurée le long de la surface de la Terre.
Une première définition de la seconde est aussi donnée en 1799 et restera valide jusqu'en 1960. La seconde était définie comme la fraction 1 / 86 400 du jour solaire moyen. Elle sera redéfinie en 1960, à l'aide des éphémérides. Les définitions de la seconde peuvent être retrouvées en détail dans l'extrait de la conférence de Nicolas Feltin.
1. Le Système International
1.1 Les unités de base
C'est finalement en 1960, que la 11 ème conférence Générale des Poids et Mesures finalise le Système International (SI). Un système d'unités doit être un système cohérent, rationalisé et couvrir l'ensemble du champ disciplinaire de la physique. Le SI actuellement en cours possède un certain nombre d'unités de base :
Grandeur physique
| Nom de l'unité SI
| Symbole de l'unité SI
|
longueur
| mètre
| m
|
masse
| kilogramme
| kg
|
temps
| seconde
| s
|
courant électrique
| ampère
| A
|
température thermodynamique
| kelvin
| K
|
quantité de matière
| mole
| mol
|
intensité lumineuse
| candela
| cd
|
1.2 Les unités dérivées
Les autres unités sont dérivées de ces unités de base. À titre d'exemple, une petite liste d'unités dérivées est donnée ci-dessous :
Grandeur physique
| Nom de l'unité SI
| Symbole de l'unité SI
| Définition de l'unité SI
|
force
| newton
| N
| kg.m.s-2
|
pression
| pascal
| Pa
| kg.m-1.s-2(=N.m-2)
|
énergie
| joule
| J
| kg.m2.s-2
|
charge électrique
| coulomb
| C
| A.s
|
potentiel électrique
| volt
| V
| kg.m-2.s-3.A-1(=J.A-1.s-1)
|
résistance électrique
| ohm
| Ω
| kg.m-2.s-3.A-2(=V.A-1)
|
inductance
| henry
| H
| kg.m2.s-2.A-2(=V.s.A-1)
|
1.3. Exemple de construction d'unité dérivée : le volt
Pour établir une unité, que ce soit une unité de base ou une unité dérivée, il faut donner : une définition, un étalon de réalisation et un étalon de représentation.
Définition du volt (V)
Le volt est la force électromotrice entre deux points d'un conducteur supportant un courant de 1 ampère quand la puissance dissipée entre ces deux points est de 1 watt.
Une fois la définition établie, on crée un étalon de réalisation, qui valide cette définition. Dans le cas du volt, l'étalon de réalisation consiste en un électromètre, figure 1. C'est une balance où d'un coté on fait intervenir le poids et de l'autre une force électrostatique qui s'exerce entre deux armatures d'un condensateur constitué d'une électrode mobile et d'une électrode fixe.
Aujourd'hui, cet étalon de référence se situe dans un musée au Laboratoire National de métrologie et d'Essais. À l'époque, le Laboratoire Central des Industries Électriques avait réalisé ces mesures et trouvait une cohérence de 3.10-6 pour une tension de V = 10 kV.
Ensuite, un étalon de représentation va être mis au point afin de permettre à l'ensemble des utilisateurs de l'industrie française l'étalonnage des appareils. Pendant longtemps l'étalon de représentation du volt consistait en pile étalon (pile de Weston, 1891). Actuellement on utilise un étalon construit à partir de diode zéner, fournissant des tensions de sortie de 1 V ; 1,018 V et 10 V.
2. La chaîne d'étalonnage au niveau international
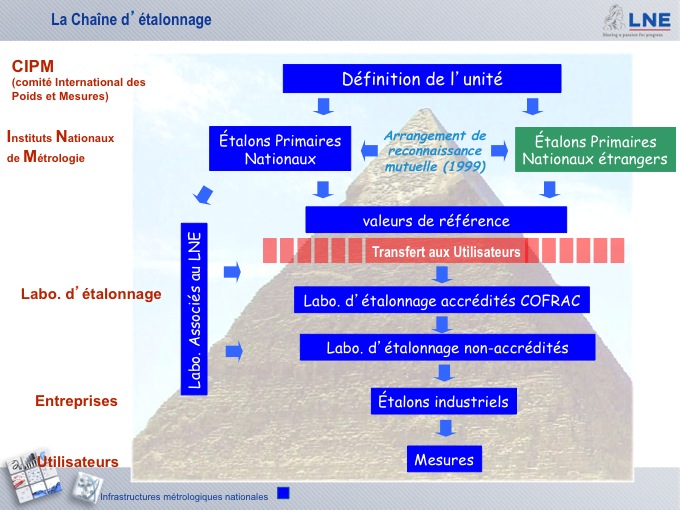
La chaîne d'étalonnage au niveau international est décrite sur la figure 2.
Le garant de la définition de l'unité est le Comité International des Poids et Mesures avec la Conférence Générale des Poids et Mesures où les grandes décisions sont prises. Ensuite, au niveau des Instituts Nationaux de Métrologie, les étalons primaires sont conservés et ces organismes sont en charge de transmettre une seule valeur de référence pour une grandeur donnée avec la plus faible incertitude possible. Puis, les valeurs de références correspondant à toutes les grandeurs définies vont être disséminées dans les laboratoires d'étalonnage accrédités COFRAC, les laboratoires d'étalonnage non accrédités, puis au niveau des industriels jusqu'aux utilisateurs qui réalisent des mesures. Si cette chaîne de traçabilité est correctement établie, les mesures sont directement traçables aux unités internationales de mesure.
Figure 2. Chaîne d'étalonnage internationale |
3. L'utilisation de nano et de micro-structures pour élaborer de nouveaux étalons
3.1 Redéfinition de la seconde
À partir de 1967, il a été donné une définition un peu plus « solide » de la seconde, à l'aide de l'atome de césium 133, atome stable avec une transition qui est très bien définie.
La seconde (s)
La seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium 133.
Cela constitue une des premières introductions de la physique quantique dans la métrologie. On s'est alors aperçu que, de cette manière, il était possible de gagner plusieurs ordres de grandeur en incertitude.
La définition de la seconde est la même que celle de 1967 mais les étalons primaires ont évolué. Les horloges atomiques modernes permettent de réaliser la seconde avec une exactitude de quelques 10-16. C'est notamment grâce à cette connaissance précise de la seconde que les américains ont pu développer le GPS.
Avec cette définition beaucoup plus « robuste » de la seconde, il a été décidé de redéfinir le mètre.
3.2 Redéfinition du mètre
Le mètre (m), depuis 1983
Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1 / c = 1 / 299 792 458 de seconde.
c est une constante fixée, c'est-à-dire qu'il n'y a pas d'incertitude liée à sa valeur. Elle sert de constante de conversion pour relier le temps et l'espace.
Finalement, la physique quantique permet d'accéder à des étalons très robustes, avec des niveaux d'incertitude très bas, qui possèdent une grande stabilité dans le temps, une grande reproductibilité et qui donnent une définition indépendante du repère spacio-temporel. Les chercheurs ont alors poursuivis leurs travaux afin de voir si d'autres effets quantiques pourraient être utilisés.
3.3 De nouveaux étalons
Des expériences basées sur des circuits quantiques pour la tension, la résistance et l'intensité ont été développées et donnent les résultats présentés ci-dessous :
Étalon de tension
| Étalon de résistance
| Étalon de courant
|
basé sur l'effet Josephson (prix Nobel 1973) | basé sur l'effet Hall quantique (prix Nobel 1985) | basé sur le blocage de Coulomb |
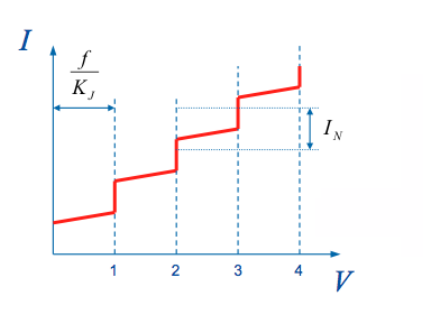
Figure 3. Mise en évidence des plateaux de tension
avec |
avec | Figure 5. Mise en évidence des plateaux de courant
|
Etalon de tension :
Pour le circuit électrique reproduisant l'effet Josephson (lien vers l'effet Josephson en détail), il est possible de tracer la caractéristique courant-tension, figure 3. En faisant varier le courant, des plateaux de tension apparaîssent. La valeur de chaque plateau de tension est remarquable par le fait qu'elle est proportionnelle à la fréquence (f) du rayonnement électromagnétique auquel est soumis le circuit (quelques GHz), au numéro de la marche (N), et inversement proportionnelle à une constante appelée KJ (J pour Josephson et KJ correspond à l'inverse du quantum de flux), définie par e la charge de l'électron et h la constante de Planck. Cet étalon assure une reproductibilité de l'ordre de 10-10.
V = N.f / KJ avec KJ ≡ 2e / h |
Etalon de résistance :
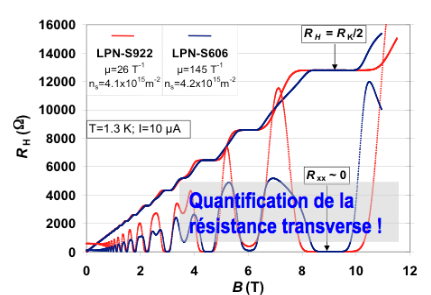
Actuellement les résistances étalons ressemblent à réseaux de barres de Hall pour lesquelles on fait appel à un autre effet quantique : l'effet Hall quantique (lien vers l'effet Hall quantique en détail).
Lorsque le circuit est soumis à un champ magnétique assez intense (jusqu'à 12 T) et à basse température (1,5K), on voit apparaitre des plateaux de valeurs de résistances, figure 4. Si l'on mesure chaque plateau, on découvre qu'il est égal à RK (constante du nom du découvreur von Klitzing et correspondant au quantum de résistance) divisé simplement par le numéro du plateau (i).
RH = RK / i avec RK ≡ h / e2 |
Une fois de plus, cette grandeur est directement reliée simplement à deux constantes fondamentales : la constante de Planck et la charge de l'électron. Cette mesure assure une reproductibilité à 10-10.
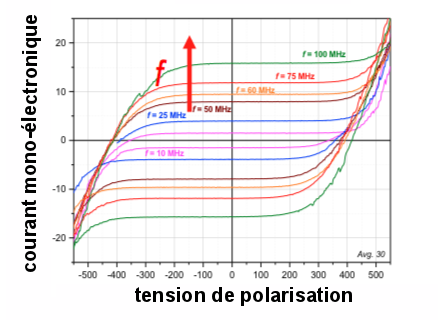
Etalon de courant :
Au début des années 80, un groupe américain du Bell labs a travaillé sur l'effet tunnel monoélectronique qui pourrait permettre à terme de définir un nouvel étalon de courant. Une décennie plus tard, le groupe Quantronique de Saclay a développé une sorte de pompe à électrons capable de contrôler le passage des électrons un à un, et a montré qu'en faisant varier la fréquence de pompage, on peut voit apparaître des plateaux de courant (les mesures de la présentation ont été réalisées au LNE), figure 5, (lien vers le blocage de Coulomb en détail).
I = e.f |
3.4 Redéfinition du kilogramme
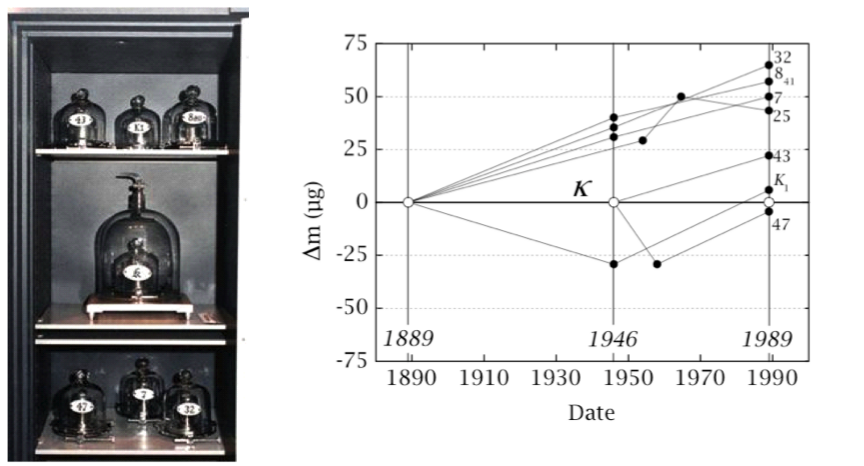
Contrairement au mètre et à la seconde, la définition du kilogramme ne repose pas, actuellement, sur un phénomène physique. L'étalon de référence du kilogramme a été coulé en 1889, il est en platine iridié, et il est défini de la sorte :
le kilogramme (kg)
1 kg est égal à la masse du prototype international du kilogramme.
A l'époque on a coulé le kilogramme, référence internationale, et de nombreux clones qui ont été dispersés dans le monde. Tous les 40 ans, des mesures sont réalisées sur ces clones afin de vérifier les étalons. Le problème, c'est qu'aujourd'hui la dispersion des mesures est de l'ordre de 5.10-8. Et pour un grand nombre d'applications, ce manque de précision n'est pas acceptable.
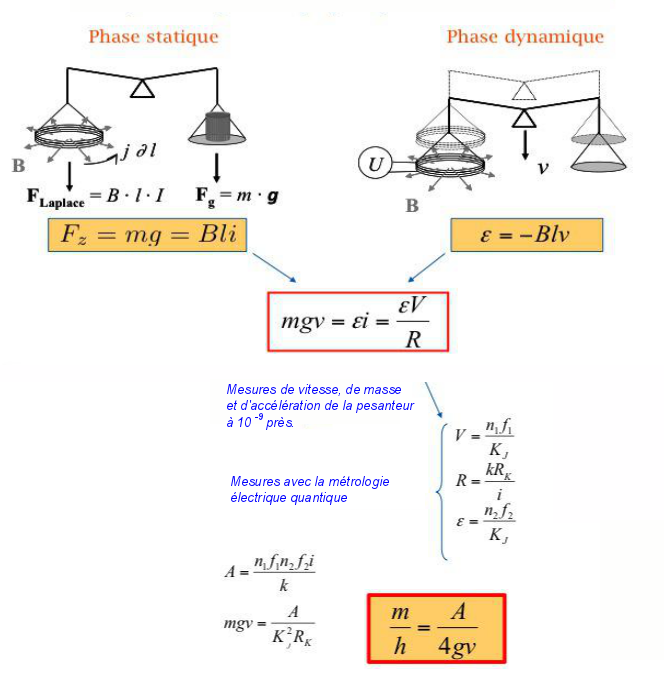
En 1975, Brian Kibble a eu une idée qui va probablement servir à la redéfinition moderne du kilogramme. L'idée est de construire une balance, avec d'un côté une force gravitationnelle réalisée à l'aide d'une masse (500 g ou 1 kg) qui vient s'opposer à une force de Laplace, obtenue en faisant passer un courant d'intensité i dans une bobine plongée dans un champ magnétique radial B (figure 7).
À l'équilibre, on a égalité entre la force de Laplace et la force gravitationnelle. Comme il est difficile de mesurer de façon très précise un champ ainsi que la longueur de l'enroulement du fil de la bobine, l'idée de Kibble est de faire une deuxième mesure en phase dynamique. Pour réaliser cette mesure, on ôte la masse du plateau, on supprime le courant parcourant la bobine et on va déplacer la bobine dans le champ magnétique radial. La tension électromotrice induite aux bornes de la bobine est alors égale au produit Blv.
À l'aide des deux expériences, on obtient une équation dont les grandeurs sont déterminées plus précisément.
Finalement la partie mécanique (vitesse, constante de gravité) se mesure très bien à 10-9 près, et de l'autre coté, la partie électrique (deux tensions et une résistance) à 10-10 près (mesures en cours au LNE). Lorsque cette mesure est réalisée, on relie ainsi la masse étalon à la constante de Planck.
Finalement, avec deux constantes fondamentales (h et e), on redéfinit à la fois le kilogramme et toutes les unités électriques.
3.5 Vers un nouveau système d'unités !
En 2017, il est prévu de changer le système d'unités. Les unités de bases comme le mètre, le kilogramme, et d'autres vont être remplacées par des constantes fondamentales. On ne connait pas encore le nombre de ces constantes fondamentales, mais ce sera un nombre restreint. Il reste encore de longues discussions pour que le système soit cohérent.
Les unités de bases compteront probablement la charge de l'électron e, la constante de Planck h, la constante de strucuture fine α, la constante de Boltzmann kB et d'autres...
C'est la veille d'une révolution importante pour la métrologie !
Voir la conférence « De la métrologie électrique quantique à la nanométrologie », par Nicolas Feltin (2014), dont est tiré cet article.
Pour citer cet article :
Le système International d'unités, Feltin, avril 2014. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/metrologie-SI.xml