Déformation des océans sous l'effet de la force de marée

Nous avons insinué précédemment que la force d'attraction lunaire provoque deux renflements diamétralement opposés dans l'océan de 69 cm de hauteur (ordre de grandeur rapide de la marée lunaire dans le cas d'un fluide parfait auto-gravitant, hétérogène). Si on s'en tenait là, on pourrait affirmer que la marée basse se produit à peu près au même moment dans deux ports situés sur le même méridien. Or, c'est loin d'être le cas.

C'est Laplace, au 19^ème siècle, qui a compris pourquoi le phénomène est plus complexe. La théorie de Newton était statique : elle faisait comme si l'océan se soulevait ou s'abaissait "gentiment", en réponse aux forces d'attraction. Pour la Terre solide nous avons vu que cela est réaliste, ses déformations sont statiques, mais, pour les océans, Laplace nous explique qu'il faut penser aux marées comme un phénomène dynamique.

Imaginez par la pensée une Terre immobile entourée par un océan, sans aucun continent, sans Lune et sans Soleil. Soulevez (toujours par la pensée !) une partie de l'océan et lâchez tout à coup. Que se passe-t-il ? Et bien, vous allez engendrer une immense vague, un tsunami, qui va se déplacer autour de la Terre. L'océan entre alors dans une sorte d'oscillation, qui sera probablement amortie par les frottements internes et finira par se calmer.

Maintenant, ajoutez la Lune (et le Soleil !). En un lieu donné sur la Terre, on peut penser aux forces d'attraction de Newton comme une espèce de pulsation, comme si toutes les 12 heures et 25 minutes, un géant soulevait l'océan. C'est l'interaction entre cette pulsation lunaire et les oscillations naturelles de l'océan qui crée les marées : c'est un phénomène dynamique.

Pensez à ces passerelles qui se mettent à osciller dangereusement lorsqu'on les traverse en cadence. Il s'agit du phénomène de résonance bien connu des physiciens. Les oscillations de l'océan, même sans forces d'attraction, sont extrêmement difficiles à décrire pour deux autres raisons encore : elles dépendent de la profondeur mais aussi de la géométrie des côtes. Les forces newtoniennes sont faciles à comprendre. En revanche, le phénomène qui en résulte est complexe et, pour le décrire, il nous faut tout à la fois utiliser des théories abstraites de l'analyse des équations aux dérivées partielles, des méthodes numériques subtiles, mais aussi les observations des marégraphes.

Pour comprendre la complexité de la dynamique océanique, commençons par supposer que l'océan est de profondeur constante et recouvre la Terre entière. Cette hypothèse faite, ouvrez n'importe quelle encyclopédie, cherchez sur internet, ouvrez n'importe quel manuel scolaire, cherchez une image illustrant le phénomène des marées... Invariablement, vous trouverez quelque chose comme la figure "statique" ci-dessous. Cette figure est fausse ! Le bourrelet est mal placé et devrait être orienté comme sur la figure "dynamique" présentée ci-dessous.

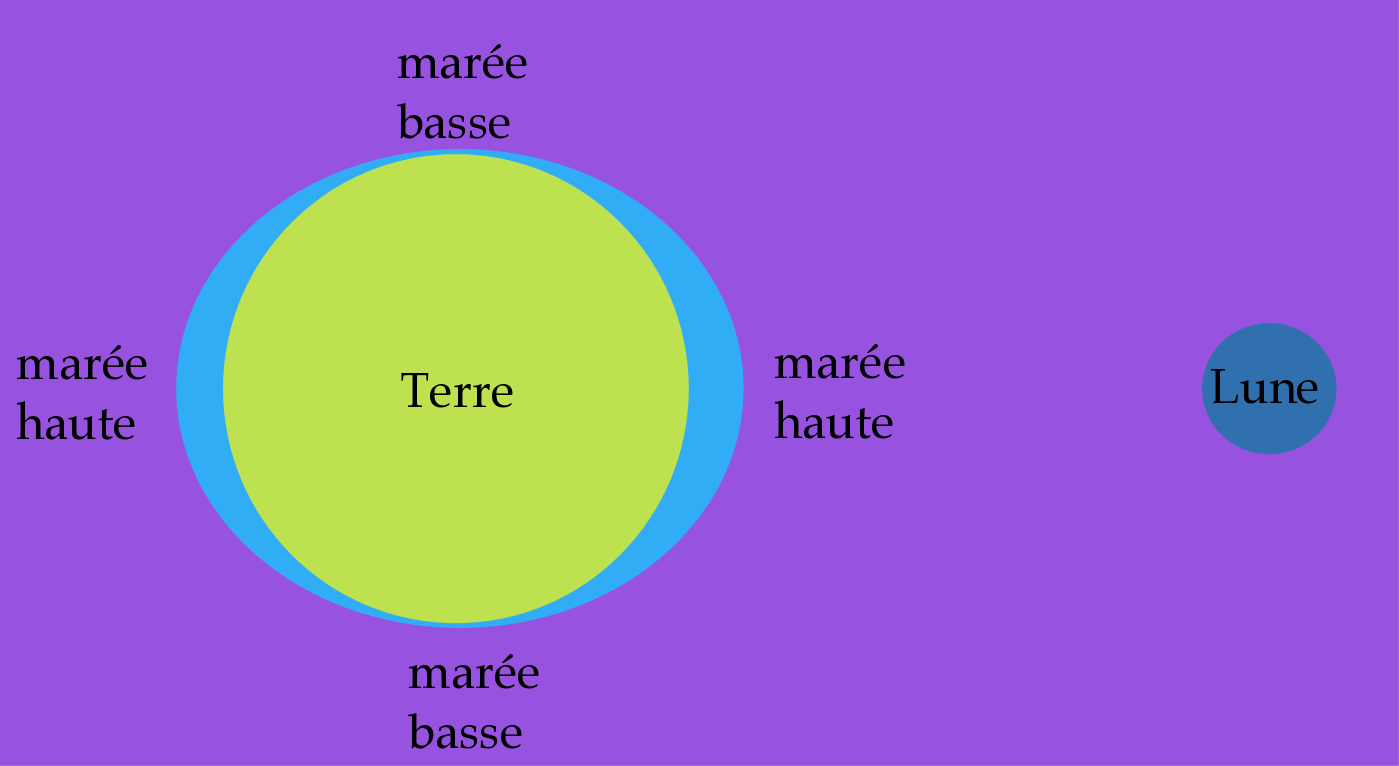
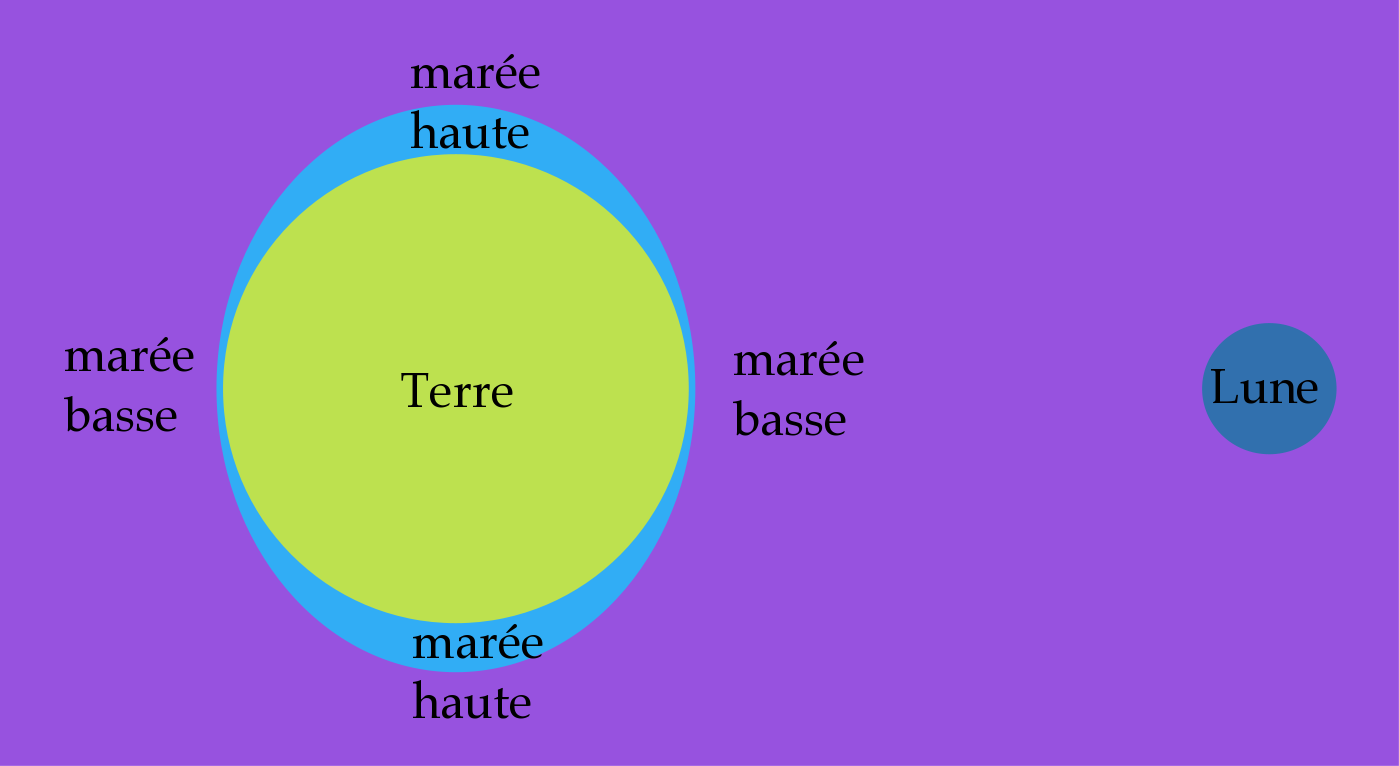
Source - © 2013 Étienne Ghys Figure 1. Modèle de marée statique Selon ce modèle "newtonien", la marée serait haute sous la Lune.

Source - © 2013 Étienne Ghys Figure 2. Structure interne théorique de Mars Selon ce modèle "laplacien", la marée serait basse sous la Lune. Si l'océan était global et homogène, c'est ce modèle qui donnerait sa vraie déformation car la réponse de l'océan à la force de marée est une réponse dynamique et non statique.

La marée serait basse sous la Lune ? Alors qu'elle devrait être haute puisque c'est là que l'attraction de la Lune est la plus forte ! Comment est-ce possible ? C'est parce que la réponse de l'océan à la force de marée est une réponse dynamique et non pas statique.

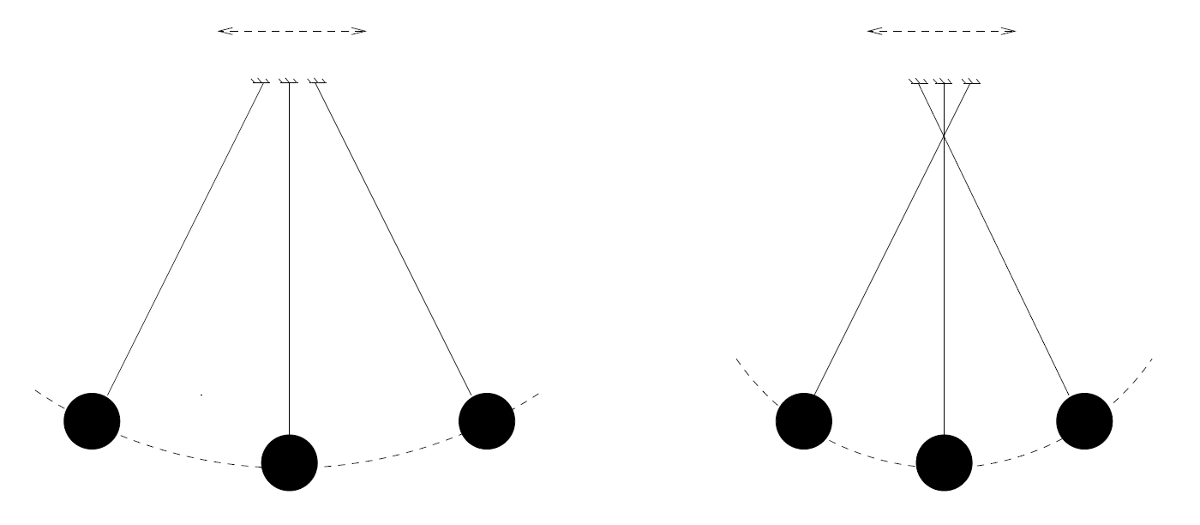
Explication. Observez un pendule qui oscille périodiquement (figure ci-dessous). Si sa longueur est d'un mètre, la période d'oscillation est d'environ deux secondes : c'est ce qu'on appelle la période d'oscillation propre. Maintenant, prenez le pendule dans la main et faites-lui subir une petite oscillation horizontale un peu plus lentement qu'une fois toutes les deux secondes. Le pendule oscille avec la période forcée que vous lui imposez, et le mouvement de votre main et du pendule sont en phase, dans le même sens en quelque sorte (partie gauche de la figure). Si, en revanche, votre main oscille plus vite qu'une fois toutes les deux secondes, les deux mouvements sont inversés, en opposition de phase (partie droite de la figure).

Source - © 2013 D'après Tadashi Tokieda, dans Souchay et al.

Figure 3. Oscillation propre – oscillation forcée

À gauche : le point de suspension oscille lentement, l'oscillation du pendule et le forçage sont en phase. À droite : le point de suspension oscille rapidement, l'oscillation et le forçage sont déphasés.

Pour la marée, c'est ce qui se passe. Si on laisse l'océan osciller, la période propre est de l'ordre de 23 h [Oscillation océan]. Or on a vu que la période de l'oscillation forcée est de l'ordre de 12 h 25 min. Comme 23 est plus grand que 12, l'océan répond moins rapidement que la force qui le sollicite, il se met en opposition de phase avec la Lune. La figure "statique" est fausse et c'est la figure "dynamique" qui est bonne !

Ce serait en tous cas ce qui se passerait s'il n'y avait pas de continents et si la profondeur des océans était constante égale à 4 km. Pour une profondeur supérieure à 20 km, ce serait la figure de gauche qui serait bonne car l'oscillation propre serait plus rapide ! Nous devons ces observations à Laplace, en 1799. Il comprit que la marée est une oscillation forcée de l'océan.

En sciences, les figures fausses ont parfois la vie dure^[1].

Tout se complique avec les vrais océans ! Ils sont de profondeur variable et sont surtout bornés par les côtes : cela complique grandement les déformations de marées.

Ces déformations se décomposent en modes dont les périodes demeurent à peu près simples : en pratique on peut dire qu'elles sont majoritairement diurnes, semi-diurnes ou mixtes suivant la position où l'on se trouve. Par contre, la forme de ces modes est bien plus complexe : certains points ne bougent pas alors que d'autres ont un mouvement important, certains points montent alors que d'autres, même situés sur un méridien commun, descendent (cf. figure ci-dessous). Ce mouvement complexe de l'océan est connu de façon complémentaire par la modélisation et par l'observation.

Décrire tout cela en détail demanderait plus de temps. Nous le gardons pour d'éventuels futurs articles dans lesquels nous évoquerons également les observations des marées, les calculs théoriques, les marées dans le système solaire et le reste de l'Univers, l'histoire des marées, etc. Il y a encore beaucoup de choses à dire !

Source - © 2007 NASA - Goddard Space Flight Center - Jet Propulsion Laboratory

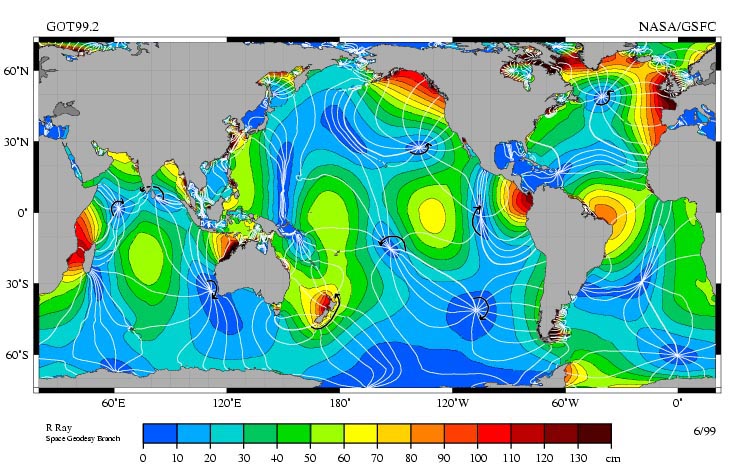
Figure 4. La marée océanique semi-diurne M2

L'amplitude de marée est indiquée par les couleurs. Les lignes blanches sont les lignes cotidales indexées toutes les heures, c'est-à-dire les lignes qui vibrent en phase. Les points où l'amplitude est nulle et où les lignes cotidales se rejoignent sont appelés points amphidromiques. Les arcs autour de ces points indiquent le sens de propagation (sens horaire dans l'hémisphère Sud et anti-horaire dans l'hémisphère Nord).

Cinq notes constituent cet exposé sur les marées :