Déformation de la Terre solide et notion d'onde de marée

Avant de lire ce texte vous saviez que les marées océaniques sont des déformations dues aux forces d'attraction de la Lune et du Soleil sur l'eau. Ce que vous ne saviez peut-être pas, c'est qu'il y a aussi des marées sur la Terre solide.

En effet, la force d'attraction de la Lune agit non seulement sur l'eau des océans mais aussi sur toute particule de Terre, qu'elle soit proche de la surface ou plus en profondeur. Dans la direction Terre-Lune cette force tend à éloigner de son centre les particules, alors que dans la direction perpendiculaire elle tend à les en rapprocher. Même si cette force agit sur l'ensemble du globe, du centre à la surface, la déformation qui en résulte, appelée marée terrestre ou marée solide, est beaucoup plus simple à calculer que celle de la marée océanique. La Terre prend approximativement la forme d'un ballon de rugby que nous avons mentionnée précédemment et dont une excroissance pointe vers la Lune et l'autre à l'opposé.

Ce bourrelet reste dans la direction Terre-Lune alors que la Terre tourne en un jour. Pour un observateur fixe à la surface de la Terre ce bourrelet se déplace donc et l'observateur monte et descend deux fois par jour. La période exacte est en fait de 12 h 25 min [12 h×29,53/28,53)] car la Lune se déplace de 1/29,53^ème de tour autour de la Terre pendant que celle-ci fait une rotation sur elle-même. Ce passage périodique du bourrelet est ce qu'on appelle une onde de marée.

Cette déformation est dite statique, car on peut faire le calcul de déformation comme si le mouvement était infiniment lent. Cette hypothèse est valide parce que le forçage de marée se propage beaucoup moins vite que les déformations de la Terre : il parcourt un tour de Terre en 12 h 25 min alors que notre planète peut osciller naturellement (le physicien parle d'oscillation libre) comme un ballon de rugby avec une période de 50 min^[1].

Pour connaître l'ampleur de la déformation plus précisément que par un argument dimensionnel nous avons deux solutions : le calcul et l'observation.

Pour effectuer le calcul, on écrit les équations de l'équilibre élastique pour une Terre quasi-sphérique soumise à la force de marée. On vient en effet de voir que l'on peut calculer les déformations de la Terre solide en ne tenant pas compte de l'accélération. Obtenir la solution est un peu calculatoire et demande quelques connaissances en mécaniques et en mathématiques. Avec la formule d'allongement donnée précédemment on trouve que la topographie créée par cette marée est de la forme :

avec le maximum, dans la direction Terre-Lune, qui vaut :

C'est quasiment la même expression que précédemment avec, au lieu du facteur "1", un coefficient $h_2$que l'on appelle nombre de Love et qui dépend des paramètres élastiques de la Terre. Ceux-ci ont connus grâce à la sismologie^[2] et indiquent que $h_2\simeq \mathrm{0,62}$, soit $h_{\max }=22\mathrm{ cm}$ pour la Lune et $h_{\max }=10\mathrm{ cm}$ pour le Soleil.

Les observations confirment-elles cette théorie ? Remarquons tout d'abord que la force d'attraction lunaire a plusieurs effets sur un instrument situé en surface terrestre. Elle exerce une force sur l'instrument et modifie donc directement la pesanteur. En déformant la Terre, elle soulève ou abaisse l'instrument par rapport au centre de la Terre et elle modifie l'attraction de la Terre elle-même. Ainsi la force de marée modifie l'intensité de la pesanteur, sa direction et la position de l'instrument. Ces quantités peuvent être mesurées respectivement avec un gravimètre (schématiquement une masse au bout d'un ressort, cf. gravimètre ci-dessous), un inclinomètre (un fil à plomb par rapport aux étoiles) et un système de positionnement (par exemple, le GPS).

Figure 1. Gravimètre supraconducteur de l'observatoire géophysique de Strasbourg enregistrant la pesanteur au cours du temps

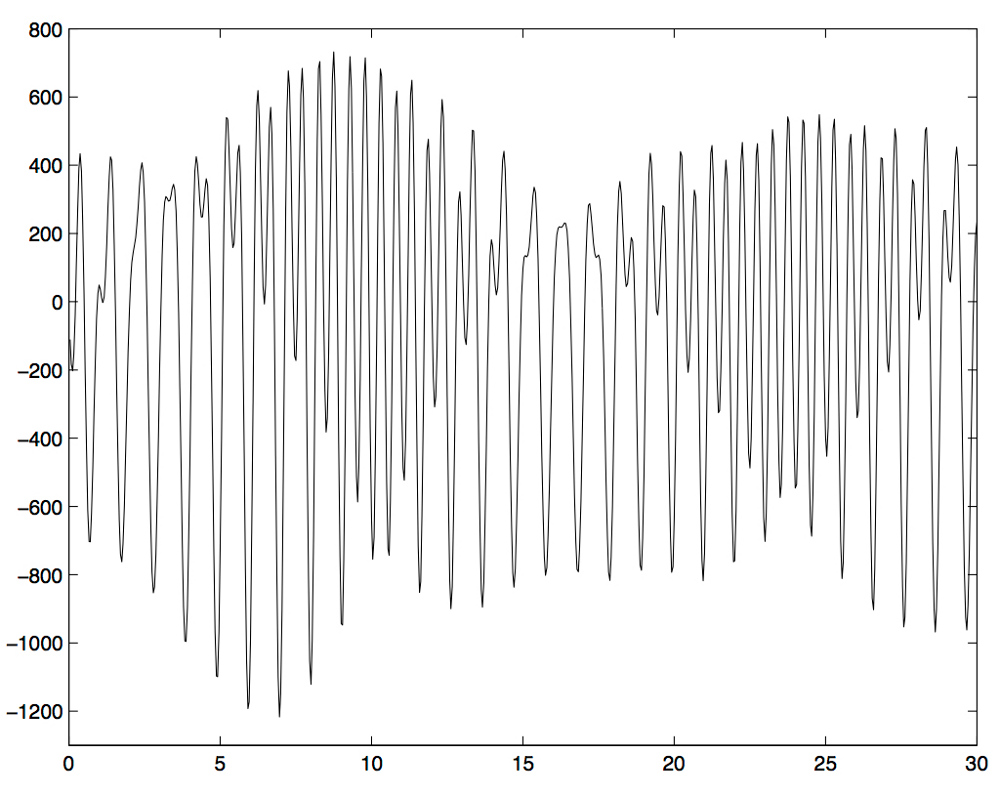
Figure 2. Variation de pesanteur à Strasbourg (ordonnées, unités arbitraires) au cours du temps (abscisse, en jours) enregistrées par le gravimètre supraconducteur Les périodes diurne et semi-diurne modulées par une période semi-mensuelle sont bien visibles.

Les calculs et les observations disent la même chose : à la surface de la Terre chacun de nous monte et descend deux fois par jour de 22 cm en moyenne par rapport au centre de notre planète. Les humains ne le sentent ni ne le voient car ce phénomène se produit lentement et à grande échelle.

On peut faire le même calcul avec les océans, en supposant leur déformation statique, ce qui comme nous le verrons plus loin est faux ! Mais cela nous donnera un ordre de grandeur. Récapitulons alors, dans le tableau ci-dessous, ce qu'on trouve pour la marée lunaire^[3] selon plusieurs hypothèses de comportement physique de l'océan.

En un point fixe de la surface terrestre, la distance zénithale d'un astre varie. Celle de la Lune varie avec une période de 12 h 25 min. Cela est vrai si on suppose qu'elle orbite dans le plan de l'équateur. Or l'équateur terrestre est incliné de 23 degrés sur l'écliptique et l'orbite lunaire est elle-même inclinée de 5 degrés sur l'écliptique. Ainsi, le mouvement lunaire dans le ciel se décompose en une sinusoïde de période 12 h 25 min mais aussi en une autre de période 24 h 50 min (durée que l'on appelle jour lunaire synodique). De plus, l'orbite lunaire n'est pas circulaire uniforme, l'orbite de la Terre autour du Soleil non plus.

Il en résulte que la force de marée luni-solaire est en fait une somme de sinusoïdes dont les amplitudes $\overrightarrow{A_n}$, pulsations ${\omega }_n$ et phases ${\phi }_n$ sont connues :

On appelle onde de marée chacun des termes de cette série. Les ondes principales sont les ondes diurnes (Soleil 24 h, Lune 24 h 50 min) et semi-diurnes (Soleil 12 h, Lune 12 h 25 min). On sait que la somme de sinusoïdes proches peut être vue comme une modulation de fréquence^[4]. La somme des ces quatre ondes peut donc être vue comme ce que nous avons déjà identifiées (cf. figure ci-dessus) : les périodes diurne et semi-diurne modulées par une période semi-mensuelle.

Cinq notes constituent cet exposé sur les marées :