Activer le mode zen
Ressource au format PDF
Mots-clés
- Zeer
- Bojito
- énergie
- évaporation
- refroidissement
Classification
Zeer ou le Frigo du Désert
01/12/2017
Résumé
Le « frigo du désert » ou Zeer, est un système de refroidissement sans électricité utilisé dans les pays chauds et secs et fondé sur l’évaporation d’eau. Après une brève description du système, un modèle thermodynamique simple est développé et permet de décrire les phénomènes physiques mis en jeu au travers de caractéristiques physiques importantes telles que la conductivité thermique, l’enthalpie de vaporisation, la capacité calorifique etc. Des expériences simples et ludiques permettent de montrer la robustesse du modèle.
Table des matières
1. Introduction
Le froid peut être bien utile, surtout quand il fait chaud ! Pas simple de conserver des aliments ou de se rafraîchir sous des températures estivales. C’est pourquoi les réfrigérateurs furent une révolution sanitaire et culturelle, ralentissant la prolifération des germes et rafraîchissant nos boissons. Mais comment faire sans eux, sans électricité, sans machine ? Comment réduire la température sans être le démon de Maxwell ? Cela semble presque impossible et pourtant nos ancêtres y arrivaient déjà il y a 5000 ans.
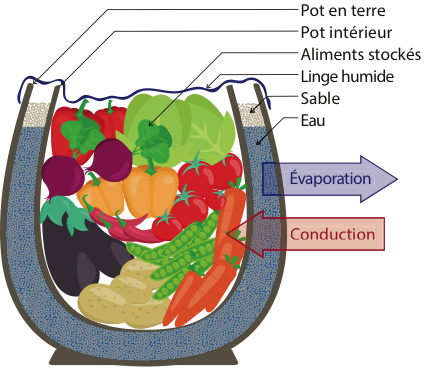
Le « frigo du désert » ou Zeer est une technique simple qui ne date pas d’hier. Ces réfrigérateurs sont composés le plus souvent de deux pots en terre imbriqués l’un dans l’autre (voir figure 1). Entre les deux, du sable les maintenant en place est imprégné d’eau. Le pot intérieur est imperméable et contient les aliments que l’on souhaite conserver au frais. Le pot extérieur est quant à lui poreux et laisse l’eau s’infiltrer jusqu’à la surface extérieure. De la même manière que l’on ressent le froid quant on sort d’un bain, les molécules d’eau vont prendre de la chaleur au système en s’évaporant, le refroidissant. En pratique, et dans de bonnes conditions, on peut observer des chutes de température de l'ordre de 5°C à 20°C !
L’invention n’est pas nouvelle. On en retrouve des traces en Égypte 2500 ans av. J.-C. et dans la Vallée de L’Indus 3000 ans av. J.-C. D’autres objets au principe similaire existent comme le Bojito Espagnol : une cruche en terre cuite perméable. L’eau contenue s’évapore partiellement à la surface et refroidit le reste. Aujourd’hui ces techniques sont encore utilisées et même repensées au cœur des enjeux écologiques. Par exemple des moucharabieh formés par des motifs creux en terre remplis d’eau sont imaginés comme systèmes de climatisation.
Dans cet article nous développons un modèle simple permettant d’expliquer la thermodynamique d’un tel système au travers de ses grandeurs clés : capacité calorifique, enthalpie de vaporisation du liquide, etc. Nous verrons que l’évolution de la température lors d’expériences simples peut être calculée, expliquée et même optimisée jusqu'à créer de la glace !
Figure 1. Schéma du Zeer. |
Le démon de Maxwell
Le démon de Maxwell est une expérience de pensée faite par le physicien du même nom pour illustrer le deuxième principe de la thermodynamique qui établit l’irréversibilité des échanges thermiques. Autrement dit, un corps chaud mis en contact avec un corps froid lui fournira de la chaleur jusqu’à être à la même température, l’inverse est impossible. Maxwell imagine dans ce cas qu’un démon devrait avoir la capacité de séparer les molécules de grande énergie cinétique (chaudes) de celles avec une plus faible énergie (froides) et répéter le processus jusqu’à observer une différence de température.
2. De l'objet millénaire au modèle
Afin de définir un modèle théorique et de concevoir des expériences de laboratoire, penchons-nous sur les paramètres importants du système.
Nous proposons, dans un premier temps, de présenter les grandeurs relatives à la modélisation. Les hypothèses et la mise en équation des phénomènes sont décrits avec précision dans la partie 4.
2.1 Paramètres du système
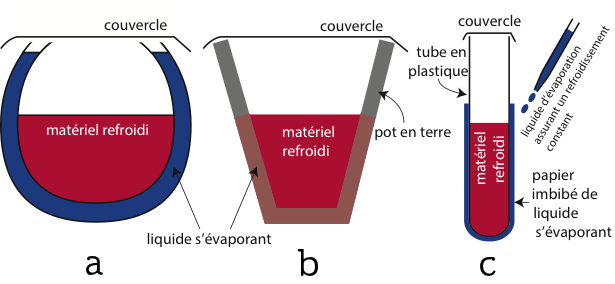
Comme discuté dans l’introduction, que ce soit pour un Zeer (figures 1 et 2a) ou un Bojito (figure 2b), l’évaporation d’un liquide à la surface du pot évacue de l’énergie thermique et refroidit le pot. À l’inverse, l’air environnant agit comme un bain thermostaté qui tend à le réchauffer. Dans le cas du Zeer, le sable sert essentiellement au maintient de la structure et ne sera pas modélisé. Il peut néanmoins, dans une certaine mesure, aider au mouillage du pot sur toute sa hauteur par effet capillaire.
Nous sommes donc en présence d’un système (Σ) dont l’énergie thermique (EΣ) diminue grâce à un flux de chaleur sortant (Φsortant) dû à l’évaporation du liquide et augmente à cause d’un flux de chaleur entrant (Φentrant) dû à la température plus élevée de l’air ambiant :
À noter que si le Zeer ou le Bojito se trouvent directement au soleil, le flux de chaleur dû au rayonnement direct (non pris en compte ici) est le plus souvent largement supérieur à celui retiré par évaporation. Le système ne se refroidit plus mais chauffe.
L'énergie thermique du système : EΣ
L’énergie du système est directement reliée à sa température T au travers de sa capacité calorifique C, c’est à dire la quantité de chaleur à lui fournir pour élever sa température de 1°C.
Ainsi EΣ = CT.
Néanmoins, rien n’indique a priori que la capacité calorifique du système ou que sa température soient homogènes. Aussi il faudrait intégrer sur l’objet ces variables locales. De plus, le champ de température ne varie pas de manière homogène mais suivant des profils liés à la géométrie, la capacité calorifique locale et la conductivité thermique locale. Notons néanmoins qu’en régime stationnaire, lorsque les flux entrant et sortant sont égaux, la température n’évolue plus et est homogène dans le tout le système.
Flux de chaleur entrant : Φentrant
Le flux de chaleur est créé entre le pot et l’air (un fluide). Il s’agit donc d’un transfert convectif et non conductif comme entre deux matériaux en contact. Il n’y a donc pas continuité de la température à l’interface. Le flux de chaleur dépend de la température du pot, la température ambiante de l’air et de la résistance thermique de l’interface.
Flux de chaleur sortant : Φsortant
Le flux de chaleur sortant est dû à l’évaporation du liquide à la surface du pot. Quand un liquide se trouve à une température inférieure à sa température d’ébullition à la pression considérée, cela signifie qu’en moyenne les molécules n’ont pas assez d’énergie pour passer à l’état gazeux. Cependant cette énergie varie d’une molécule à l’autre et au cours du temps. Aussi, certaines molécules à l’interface avec l’air accumulent suffisamment d’énergie et passent à l’état gazeux. Comme seules les molécules les plus énergétiques passent à l’état gazeux, l’énergie moyenne du reste des molécules diminue. Exactement comme dans l’expérience du démon de Maxwell !
Ainsi le flux d’énergie sortant dépend de la chaleur latente d’évaporation du liquide, c’est à dire l’énergie nécessaire au liquide pour passer à l’état gazeux par unité de masse et il dépend aussi du flux de masse d'eau évaporée.
2.2 Présentation des modèles expérimentaux
Dans un premier temps nous étudierons le principe du vrai Botijo (cas le plus simple) en utilisant un pot en terre remplis d’eau (figure 2b). Pour ce qui est du Zeer, nous le modéliserons par un tube en plastique contenant de l’eau et entouré d’un papier imbibé soit d’éthanol soit d’éther faisant ainsi varier les liquides et donc les chaleurs latentes d’évaporation :
EAU | ETHANOL | ETHER | |
Densité ρ (kg.m-3) | 1 | 0,789 | 0,713 |
Capacité calorifique C à 298 K (kJ.kg-1.K-1) | 4,18 | 2,44 | 2,36 |
Chaleur latente Lv (kJ.kg-1) | 2442 | 918 | 365 |
Pression de vapeur saturante Peq (kPa) | 2,34 | 5,8 | 58,6 |
3. Expériences de refroidissement
3.1 Le Bojito
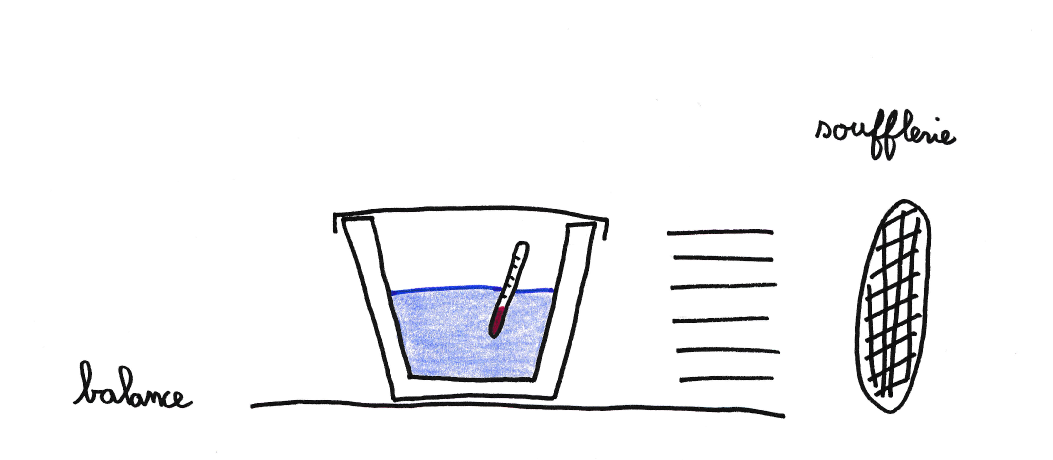
Le Bojito est le système le plus simple à étudier. Pour cela, un pot en terre poreux de 3 L est rempli de 1,85 L d’eau (figure 3). Bien que légèrement évasé, il peut être assimilé à un cylindre d’une hauteur de 20 cm pour un diamètre moyen de 14 cm. Le pot pesant 1554 g, la capacité totale du système est de 9900 J/K en considérant une capacité calorifique massique pour la terre de 1380 kJ/kg/K. Durant toute l’expérience une soufflerie crée un vent de 10 ± 2 m/s et l’humidité, mesurée grâce à un hygromètre, reste entre 72% et 74%. La température ambiante reste constante à T0 = 21°C.
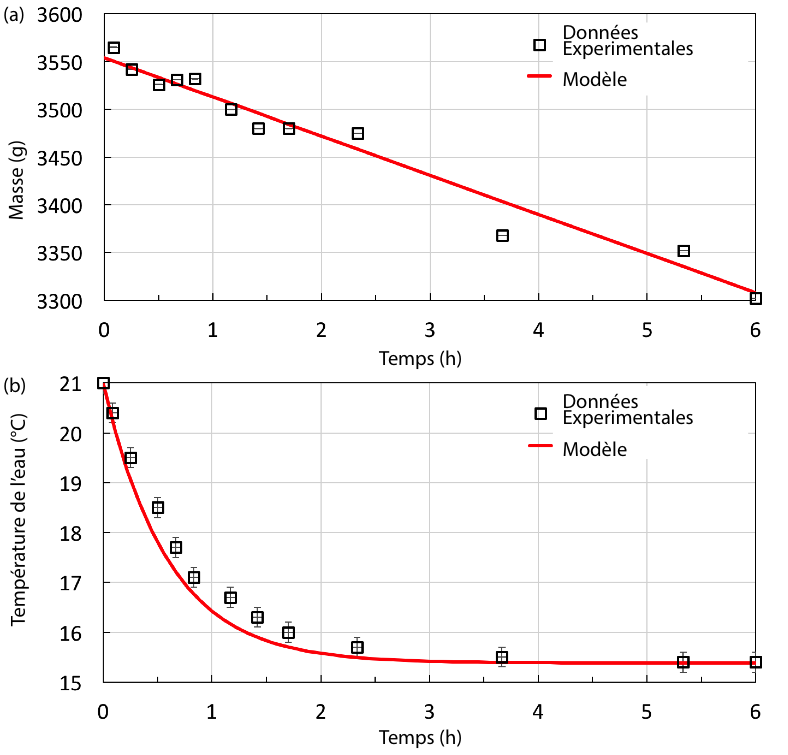
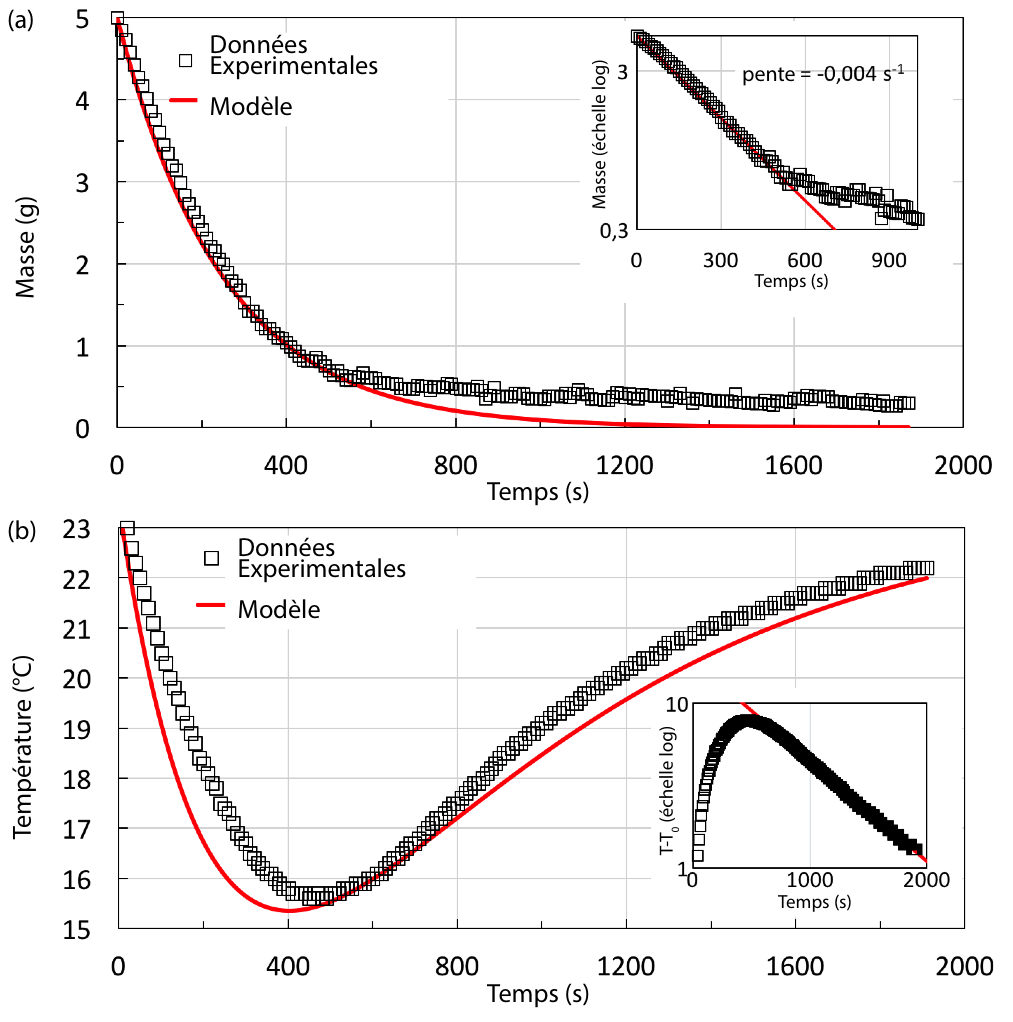
Le poids du système est mesuré tout au long de l’expérience grâce à une balance (figure 4a). Durant l’expérience le volume d’eau évaporé est bien inférieur au volume total. Aussi, la vitesse d’évaporation peut être considérée constante comme le montre l’évolution linéaire de la masse : la surface d’évaporation varie très peu. Un ajustement permet de mesurer la masse d'eau s'évaporant à 41 ± 5 g/h (courbe rouge figure 4a). De même la capacité calorifique et résistance thermique restent a priori constantes. La masse d'eau s'évaporant varie linéairement en fonction du temps.
La température relevée au centre de pot par un thermomètre (figure 4b) diminue de 5,7°C sur 4 h et finit par se stabiliser à 15,3°C lorsque les flux de chaleur s’équilibrent (voir section 2.3). La courbe rouge de la figure 4b représente la solution de l’équation de l’évolution de la température (équation E) au centre du système. La température décroît exponentiellement avec le temps.
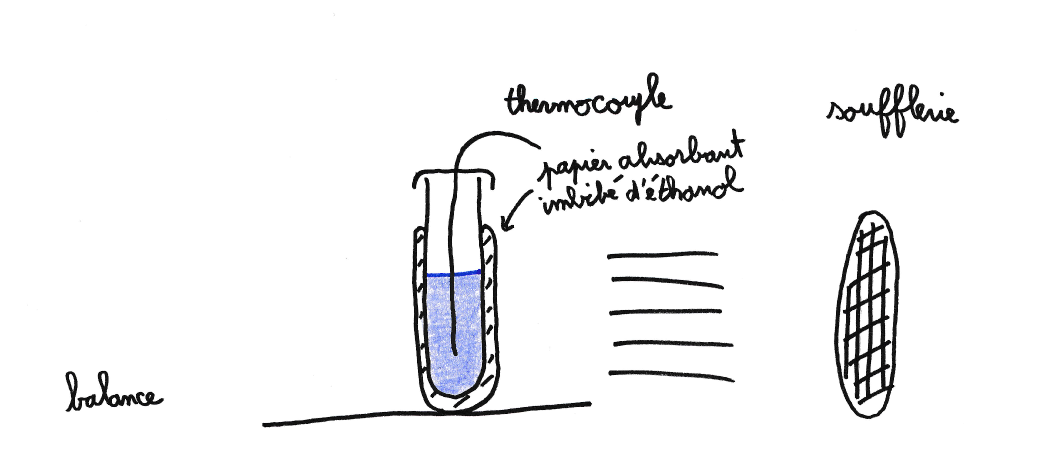
3.2 Le modèle du Zeer
Le Zeer est un système un peu différent dans lequel la masse refroidie et le liquide s’évaporant ne sont pas les mêmes (figure 1 et 2a). Afin de le modéliser, un tube en plastique de 30 mm de diamètre et 90 mm de haut enroulé dans du papier absorbant est utilisé (figure 5). Il est rempli avec 50 mL d’eau distillée représentant le système à refroidir. La capacité calorifique et la résistance thermique du tube dont la paroi fait seulement 1 mm sont largement négligeables devant celle de l’eau et ne seront pas prises en compte dans le modèle. Le papier absorbant est imbibé de 5 g d’éthanol qui, en s’évaporant, refroidira le système. Le tout est placé devant une soufflerie sous un vent de 3,2 ± 0,3 m/s. On peut remarquer que la pression partielle de l’éthanol dans l’air ambiant est négligeable tout au long de l’expérience favorisant une évaporation rapide. La masse d’éthanol est mesurée en continu par une balance (figure 6a) et la température de l’eau est mesurée au centre du tube grâce à un thermocouple (figure 6b).
Contrairement au cas du Botijo, l’évolution de la masse d’éthanol n’est pas linéaire. Cela vient du fait qu’au cours de l’expérience la totalité de l’éthanol s’évapore et que la surface d’évaporation n’est pas constante : à cause de la gravité, l’éthanol liquide s’accumule en bas du tube alors que le sommet sèche. Au premier ordre, la surface d’évaporation diminue donc linéairement avec la masse évaporée. Si l’on considère que la vitesse d’évaporation est proportionnelle à cette surface, on obtient immédiatement que la l’évolution de la masse décroit exponentiellement.
3.3 Toujours plus froid !
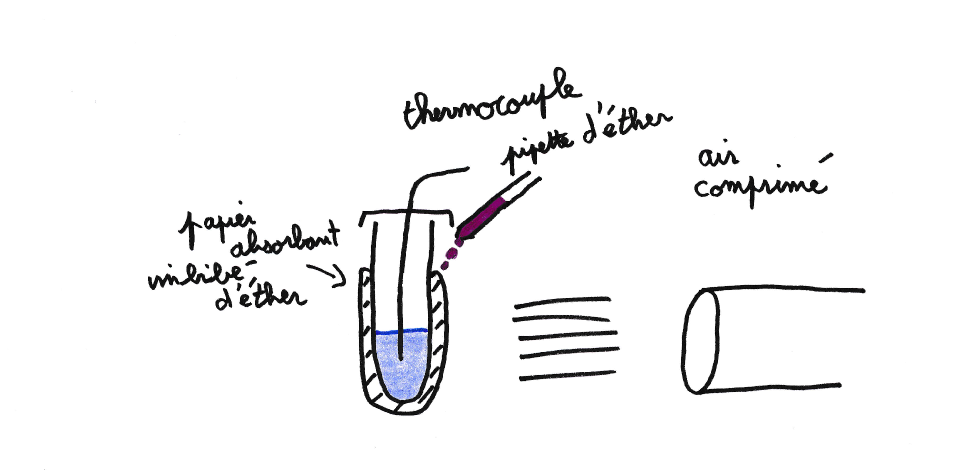
Cette dernière expérience pousse ce système de refroidissement à ses limites en jouant sur les paramètres du modèle. Afin de maximiser le refroidissement il faut minimiser la capacité calorifique du système et utiliser un liquide s’évaporant rapidement avec une chaleur latente d’évaporation la plus grande possible. Ainsi seul 9 mL d’eau sont placés dans une petit tube en plastique de 5 mm de diamètre et 50 mm de long enroulé de papier absorbant imbibé d’éther. Ce dernier est ajouté de manière continue avec une pipette (voir figure 7) afin de ne pas en manquer. La quantité versée est mesurée afin de déterminer le flux de masse d'eau évaporée. Le tout est placé dans un flux d’air comprimé de 10 ± 2 m/s pour augmenter la vitesse d’évaporation. Une conséquence d’un tel vent est qu’une partie de l’éther (1-ϕ) est soufflée de la surface avant même d’être évaporée. ϕ devra donc être estimé. De plus l’éther ajouté est à température ambiante ce qui apporte une quantité d’énergie non négligeable. Ceci est pris en compte dans le modèle en considérant qu’avant de s’évaporer l’éther ajouté est abaissé à la température du système. Enfin avec un si petit système, la sonde de température (thermocouple) n’est plus forcement négligeable et peut notamment conduire la chaleur au travers du fil.
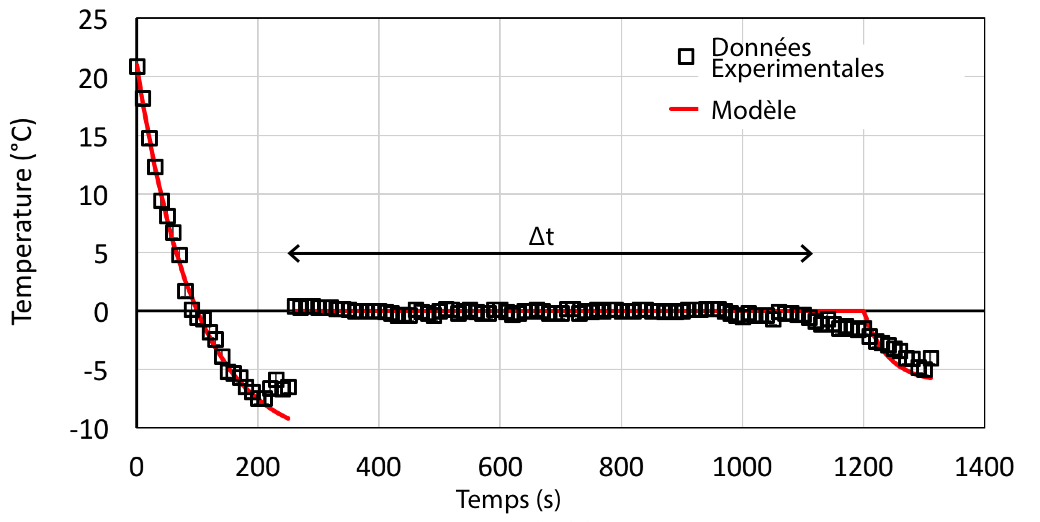
La figure 8 représente l’évolution de la température en fonction du temps. Au début de l’expérience la température chute très vite de 1°C toute les 3 s. Au bout de deux minutes elle devient négative : l’eau est en surfusion ! Quand la température atteint -7°C l’eau se transforme partiellement en glace et la température remonte brutalement à 0°C où elle se stabilise jusqu’à ce que toute l’eau soit transformée en glace. Ainsi ce n’est qu’après plus de 16 minutes que la température se remet à descendre.
Le paramètre ϕ du modèle est déterminé par l’ajustement de la première partie de la courbe. Dans notre cas ϕ = 78 ± 5% c’est à dire que 22 ± 5% de l’éther est perdu à cause du vent. Ensuite la durée du plateau peut être estimée théoriquement. En effet connaissant la température de l’eau au début du changement d’état, son enthalpie de changement d'état et les flux de chaleur, on peut déduire qu’il faut ∆t = 780 ± 100 s. Expérimentalement ∆t = 860 ± 100 s ce qui est en bon accord.
Une dernière remarque est la faible chute de température lorsque l’eau est entièrement solide. En effet la capacité calorifique de la glace est deux fois plus faible que celle de l’eau. D’après le modèle une chute très brutale devrait être observée. L’origine de cette faible évolution est attribuée à la formation importante de glace par condensation sur le papier après plusieurs minutes. Cette transformation requérant de l’énergie, cela peut expliquer que le ∆t théorique soit sous estimé et gêne l’évaporation de l’éther ce qui ralentit le refroidissement.
L’eau refroidit rapidement jusqu’à atteindre un état de surfusion à environ -7°C au bout de 240 s. Puis l’eau passe progressivement à l’état solide durant Δt et la température se stabilise à 0°C. Quand toute l’eau est à l’état solide, la température diminue de nouveau. La courbe rouge correspond aux solutions données par l’équation (E). |
4. Modélisation du système
4.1 Bilan énergétique du système
4.1.1 L'énergie thermique du système : EΣ
L’énergie du système est directement reliée à sa température T au travers de sa capacité calorifique C, c’est à dire la quantité de chaleur à lui fournir pour élever sa température de 1°C.
Ainsi EΣ = CT.
Néanmoins, rien n’indique a priori que la capacité calorifique du système ou que sa température soient homogènes. Aussi il faudrait intégrer sur l’objet ces variables locales. De plus, le champ de température ne varie pas de manière homogène mais suivant des profils liés à la géométrie, la capacité calorifique locale et la conductivité thermique locale. Notons néanmoins qu’en régime stationnaire, lorsque les flux entrant et sortant sont égaux, la température n’évolue plus et est homogène dans le tout le système.
Dans notre cas, le Zeer comme le Botijo ont des géométries proches de celle d’un cylindre. Quant à la capacité calorifique, elle est constante en première approximation. Or, si l’on considère un cylindre homogène (C constant) à la température T plongé dans un milieu à la température T0, la température au centre va tendre vers T0 de manière exponentielle après un court régime transitoire dû à l’inertie thermique du système. On peut considérer que l’objet se comporte comme un condensateur.
Ainsi, après un court régime transitoire, la température moyenne du système évolue comme la température prise au centre. Aussi nous considèrerons un modèle dont la capacité calorifique et la température sont homogènes.
4.1.2 Flux de chaleur entrant : Φentrant
Le flux de chaleur est créé entre le pot et l’air (un fluide). Il s’agit donc d’un transfert convectif et non conductif comme entre deux matériaux en contact. Il n’y a donc pas continuité de la température à l’interface. Néanmoins le flux de chaleur est parfaitement décrit par la loi empirique de Newton :
Avec T la température du pot, T0 la température ambiante de l’air et R la résistance thermique de l’interface. Le coefficient de proportionnalité dépend énormément des conditions expérimentales. Il change notamment avec la nature de la surface (type de pot, humidité, etc.) mais aussi avec la convection de l’air (vent, gradient de température, etc.). Nous ne pourrons donc déterminer ce coefficient mais il s’agira d’un paramètre d’ajustement dans notre modèle.
4.1.3 Flux de chaleur sortant : Φsortant
Le flux de chaleur sortant est dû à l’évaporation du liquide à la surface du pot. Quand un liquide se trouve à une température inférieure à sa température d’ébullition à la pression considérée, cela signifie qu’en moyenne les molécules n’ont pas assez d’énergie pour passer à l’état gazeux. Cependant cette énergie varie d’une molécule à l’autre et au cours du temps. Aussi, certaines molécules à l’interface avec l’air accumulent suffisamment d’énergie et passent à l’état gazeux. Comme seules les molécules les plus énergétiques passent à l’état gazeux, l’énergie moyenne du reste des molécules diminue. Exactement comme dans l’expérience du démon de Maxwell ! Ainsi le flux d’énergie sortant est donné par :
Avec Lv la chaleur latente d’évaporation du liquide, c’est à dire l’énergie nécessaire au liquide pour passer à l’état gazeux par unité de masse et le flux massique de matière évaporée.
Le flux de masse s’évaporant est très délicat à estimer. Au premier ordre, la vitesse d’évaporation d’un liquide est donnée par :
avec S la surface d’évaporation (celle du pot dans notre cas), Peq la pression de vapeur saturante du liquide s’évaporant et H l’humidité relative correspondante, c’est à dire le ratio de la pression partielle du liquide dans l’air avec Peq. Ainsi plus l’humidité est faible plus l’évaporation du liquide à la surface du pot est rapide. Le vent est également un paramètre extrêmement important. En effet il permet d’homogénéiser la pression partielle en liquide. Comme le liquide s’évapore à la surface du pot, l’humidité est localement bien plus importante que loin du pot. Ainsi l’évaporation et donc le refroidissement est bien plus rapide dans des environnements secs et ventés.
L’épaisseur du pot et sa porosité sont également importantes. Plus le pot est épais et étanche moins le flux d’eau vers l’extérieur est grand et peut potentiellement devenir le facteur limitant du taux d’évaporation.
Ces paramètres sont délicats à prendre en compte et une dynamique précise dépend énormément du cas pratique considéré. Or nous verrons que dans les différents cas expérimentaux, il est facile de mesurer ce flux, de l’ajuster et de l’injecter dans notre modèle.
4.1.4 Équation de l'évolution de la température
Une balance énergétique nous donne donc une équation de l’évolution de la température du système au cours du temps :
(équation E) |
Avec T la température moyenne du système assimilé à sa température centrale (voir partie 2), T0 la température de l’air ambiant, C la capacité calorifique moyenne du système, Lv la chaleur latente d’évaporation du liquide à la surface du pot, le flux de masse s’évaporant (mesuré expérimentalement) et R la résistance thermique entre le pot et l’air ambiant qui est le seul et unique paramètre d’ajustement.
A priori, comme dans tous les problèmes de flux de chaleur, la taille du système est primordiale. En effet sa capacité calorifique totale est proportionnelle à son volume alors que les flux de chaleurs sont eux proportionnels à sa surface. Cependant, dans notre cas, le système est refroidi par l’évaporation du liquide à sa surface et lui est proportionnel si la surface reste mouillée (voir partie 2). Aussi, au premier ordre, l’état stationnaire est indépendant de la taille du système : la température n’évolue plus car les flux de chaleur sont égaux. Seul le temps pour y parvenir en dépend : plus le pot est grand, plus il faudra de temps pour le refroidir et atteindre l’équilibre. Un modèle à échelle réduite est donc pertinent pour étudier la température minimale atteignable avec un Botijo ou un Zeer.
4.2 Modélisation du Botijo
La vitesse d’évaporation peut être considérée constante comme le montre l’évolution linéaire de la masse : la surface d’évaporation varie très peu. Un ajustement permet de mesurer = - 41 ± 5 g/h (courbe rouge figure 4a). De même la capacité calorifique et résistance thermique restent a priori constantes.
La courbe rouge de la figure 4b représente la solution de l’équation de l’évolution de la température (suivant l'équation E) au centre du système :
Avec τ = RC le temps caractéristique de l’inertie thermique du système. La résistance R est déduite par la valeur de T à l’équilibre. En effet, l’équation E pour un état stationnaire donne :
Aussi avec seulement un paramètre d’ajustement, le modèle décrit de manière extrêmement convaincante l’évolution de la température. On peut remarquer que la valeur théorique pour la résistance thermique calculée à partir d’un modèle de cylindre infini d’eau serait du même ordre de grandeur : 2,2 ± 0,1 W/K. La différence peut venir du faire que la terre est un meilleur isolant thermique que l’eau faisant grimper la résistance thermique réelle du système.
4.3 Modélisation du Zeer
Contrairement au cas du Botijo, l’évolution de la masse d’éthanol n’est pas linéaire. Cela vient du fait qu’au cours de l’expérience la totalité de l’éthanol s’évapore et que la surface d’évaporation n’est pas constante : à cause de la gravité, l’éthanol liquide s’accumule en bas du tube alors que le sommet sèche. Au premier ordre, la surface d’évaporation diminue donc linéairement avec la masse évaporée. Si l’on considère que la vitesse d’évaporation est proportionnelle à cette surface, on obtient immédiatement que la l’évolution de la masse décroit exponentiellement :
Avec la quantité initiale d’éthanol (5 mL) et le temps caractéristique d’évaporation. En ajustant l’évolution de la masse (courbe rouge figure 4a) on détermine que = 250 ± 10 s. On peut noter qu’après 500 s l’évolution de la masse ne semble plus décroître exponentiellement. En réalité la masse additionnelle correspond à de l’eau ayant condensé sur le papier refroidi par l’évaporation de l’éthanol.
L’évolution de la température peut alors être calculée à partir de l'équation E en injectant la solution exponentielle de la vitesse d’évaporation :
(équation S) |
Avec τ = RC. Encore une fois, le seul paramètre à déterminer est la résistance thermique du système R.
La figure 6b montre que le système refroidit d’abord sous l’effet de l’évaporation de l’éthanol mais, après 800 s, presque tout l’éthanol s’est évaporé et seul le flux de chaleur entrant persiste : le tube se réchauffe (2). Dans ce cas, le terme de droite de l’équation E devient simplement proportionnel à la différence de température et T(t) évolue comme . Ce comportement est confirmé expérimentalement (voir le tracé de T en échelle log-log encart figure 6b) et R est donc obtenu en fitant la solution théorique (droite rouge de l’encart).
Ainsi est obtenue une évolution semi-théorique de l’évolution (équation S) de la température du Zeer tracée en rouge sur la figure 6b. D’une part cette prédiction est en bon accord avec les mesures mais reproduit la décroissance de la température, son minimum et son retour à température ambiante. Un Zeer peut donc lui aussi être décrit de manière convaincante par notre modèle.
5. Conclusion
Le Zeer et le Botijo sont des systèmes thermodynamiques complexes utilisant l’évaporation d’eau à leur surface pour refroidir leur contenu. Il semble a priori compliqué de modéliser l’évolution de la température au centre de ces objets. En effet, celle-ci va dépendre de leur capacité calorifique, de la conduction de chaleur au sein du système, de la dynamique d’évaporation de l’eau à la surface et de la dynamique de réchauffement convectif à sa surface.
Néanmoins, nous avons montré qu’en faisant quelques hypothèses (homogénéité du système, inertie thermique faible en comparaison au temps de refroidissement etc.) il est possible de décrire ces systèmes avec une simple équation sur les flux de chaleur. Seuls deux paramètres restent difficiles à estimer a priori : le flux d’eau s’évaporant et la résistance thermique du système qui sont respectivement mesurés et ajustés dans les expériences présentées. En effet ils dépendent par exemple de la terre cuite qui est un matériau poreux dont la composition et l’aspect de surface change énormément d’un pot à l’autre, du flux d’air autour du pot et de l’humidité. Cependant, comprenant l’influence qualitative de ces paramètres, il est possible d’optimiser le système de Zeer jusqu’à former de la glace presque aussi bien que ne le ferait le Démon de Maxwell !
Pour citer cet article :
Zeer ou le Frigo du Désert, Chemin, décembre 2017. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/frigo-desert.xml