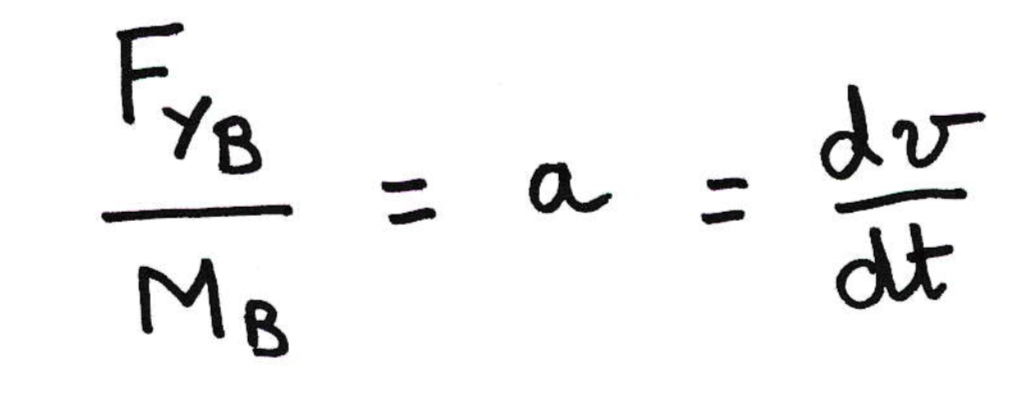Résolution numérique en langage python : Comment faire rebondir une balle avec de l'énergie cachée

Dans le premier article « Résolution numérique en langage python : la chute libre - 1 », nous nous sommes intéressés à la chute libre d'une balle de tennis, sans vitesse initiale et sans prendre en compte les frottements de l'air, jusqu'au moment où elle touche le sol.

Dans ce deuxième article, nous allons mettre en évidence le tranfert d'énergie lors du rebond entre deux balles posées initialement l'une sur l'autre et lâchées sans vitesse. La vidéo ci-dessous présente l'expérience que nous modéliserons ensuite à l'aide d'un programme en langage Python.

Nous proposon de présenter le programme python, la physique en jeu et son codage de manière linéaire le long de l'article.

Dans un premier temps, on importe les bibliothèques python nécessaires au traitement des données et à l'affichage des graphiques, figure 1.

Figure 1.  Importation des bibliothèques python utilisées

Nous lâchons une balle de tennis posée sur un ballon de basket d'une hauteur donnée. Une fois que les deux balles ont quitté la main, la seule force qui s'applique sur elles est la force de gravité, figure 2. On pourra considérer que la force de réaction qu'éxerce le ballon de basket sur la balle de tennis disparait quasiment immédiatement après le lâché. Dans notre étude, les frottements de l'air ne sont pas pris en compte tout comme la dissipation d'énergie interne des balles. Nous ne cherchons pas ici à retrouver les valeurs exactes de la vidéo mais proposons une étude simplifiée pour s'intéresser à la physique mise en jeu.

Figure 2.  Schéma de l'étude correspondant à l'instant du lâché des balles

On renseigne dans le code les paramètres relatifs aux deux balles : masse, rayon, constante de raideur, figure 3.

Dans la modélisation proposée ici, le rebond des balles est représenté à l'aide d'un modèle masse-ressort linéaire. Les constantes de raideurs sont fixées pour tout le mouvement et correspondent à une petite déformation (cas d'un lâché sans vitesse initiale).

Figure 3.  Définition des deux objets

On renseigne ensuite les valeurs de constante (gravitation), paramètre (pas de temps) et les conditions initiales (hauteur du lâché, vitesse initiale), figure 4.

On définit pour les positions et vitesses des deux balles des vecteurs (np.array) qui vont contenir les valeurs au cours du mouvement.

Figure 4.  Initialisation des grandeurs

Maintenant, nous appliquons la méthode d'Euler pour coder le mouvement, figure 5.

De la même manière que nous l'avons fait dans le premier article, nous calculons à chaque instant la position et la vitesse des balles à l'aide d'une méthode numérique de résolution de l'équation différentielle basée sur le schéma d'Euler.

Figure 5.  Résolution numérique du mouvement des balles au cours du temps

On fixe, arbitrairement, le temps de calcul à 1,7 s.

On définit le nombre de points "nb_points" du calcul. Il est choisi à l'aide du temps total ("temps_total") avec un échantillonnage au pas de temps "dt" défini précédemment. Le nombre de points est nécessairement un entier, on utilise la fonction int pour ne garder que la partie entière.

On définit alors le vecteur "temps" de la manière suivante :

Définition d'un vecteur (linspace) partant du temps au début (0), au temps final "nb_points", contenant "nb_points+1" éléments (0 et les nb_points autres valeurs), multiplié par le pas de temps (dt).

Dans cet exemple on a fixé le temps au cours duquel on va modéliser la trajectoire des balles, on choisit alors d'utiliser une boucle for de la manière suivante :

Pour un indice d'itération "i" partant de 0, la boucle se répétant "nb_points", avec une incrémentation de 1, on calcule les vitesses et positions des deux balles.

Pour chaque pas de temps, on calcule les forces s'exerçant sur la balle de tennis et le ballon de basket. Lorsqu'ils sont en chute libre, seul le poids intervient, figure 6. Par contre, lors du rebond, on prend en compte les constantes de raideurs : on note sur le schéma les forces de rappel FK_B et fk_t respectivement pour le ballon de basket et la balle de tennis, figure 7.

Figure 6.  Représentation des forces avant le rebond

Figure 7.  Représentation des forces lors du rebond

À chaque pas de temps, on calcule les forces s'exerçant sur chaque balle à l'aide d'un test sur leur position par rapport au sol et entre elles.

Ce qui donne, en prenant l'exemple du ballon de basket, lorsqu'on projette les forces sur l'axe vertical et que l'on appelle F_YB la résultante :

Ensuite, comme nous l'avons fait dans le premier article sur la chute libre, nous calculons à chaque instant la vitesse et la position des balles à l'aide d'une méthode numérique de résolution de l'équation différentielle basée sur le schéma d'Euler.

On rappelle que l'approximation de la dérivée par une fonction ∆ n'est raisonnable que si la variation de la vitesse entre les deux instants est toute petite.

D'où le calcul de la vitesse pour chaque pas de temps :

De la même manière, la position est calculée à chaque pas de temps.

Reprenons alors sereinement le programme python, figure 5. À chaque itération de la boucle, nous venons concaténer les valeurs des vitesses et des positions des deux balles, de la manière suivante :

Le vecteur (array) "vit_yB" comprend toutes les valeurs des vitesses calculées à chaque itération pour le ballon de basket. La fonction np.append permet de concaténer (rajouter un élément au vecteur) la valeur calculée "vY_B" à la suite des éléments précédents contenus dans "vit_yB".

Lorsque l'on sort de la boucle, figure 5, (les dernières instructions ne sont pas indentées sur la boucle for), on demande d'afficher le nombre de points calculés "nb_points". L'usage de la fonction len (pour length = longueur) est très utile pour connaitre la taille (le nombre d'éléments) contenus dans un vecteur.

Le code renvoie les éléments suivants, figure 8.

Figure 8.  Sortie du code de la figure 5

Il est important de noter que si la chute libre d'un corps admet une solution analytique simple et connue de tous, dans le cas d'une chute avec rebond, la solution analytique est plus compliquée et n'est pas du programme de lycée. Dans cette modélisation, nous donnons simplement les instructions pour effectuer un calcul à chaque pas de temps en prenant en compte la physique : quelles forces agissent sur les balles pour calculer leurs vitesses et leurs positions.

Nous avons fourni les lois de la physique au calculateur pour qu'il soit capable de nous renvoyer position et vitesse des balles à chaque instant.

On peut ensuite tracer la représentation graphique des trajectoires des deux balles en fonction du temps, figure 9.

Figure 9.  Code python du tracé des positions des deux balles

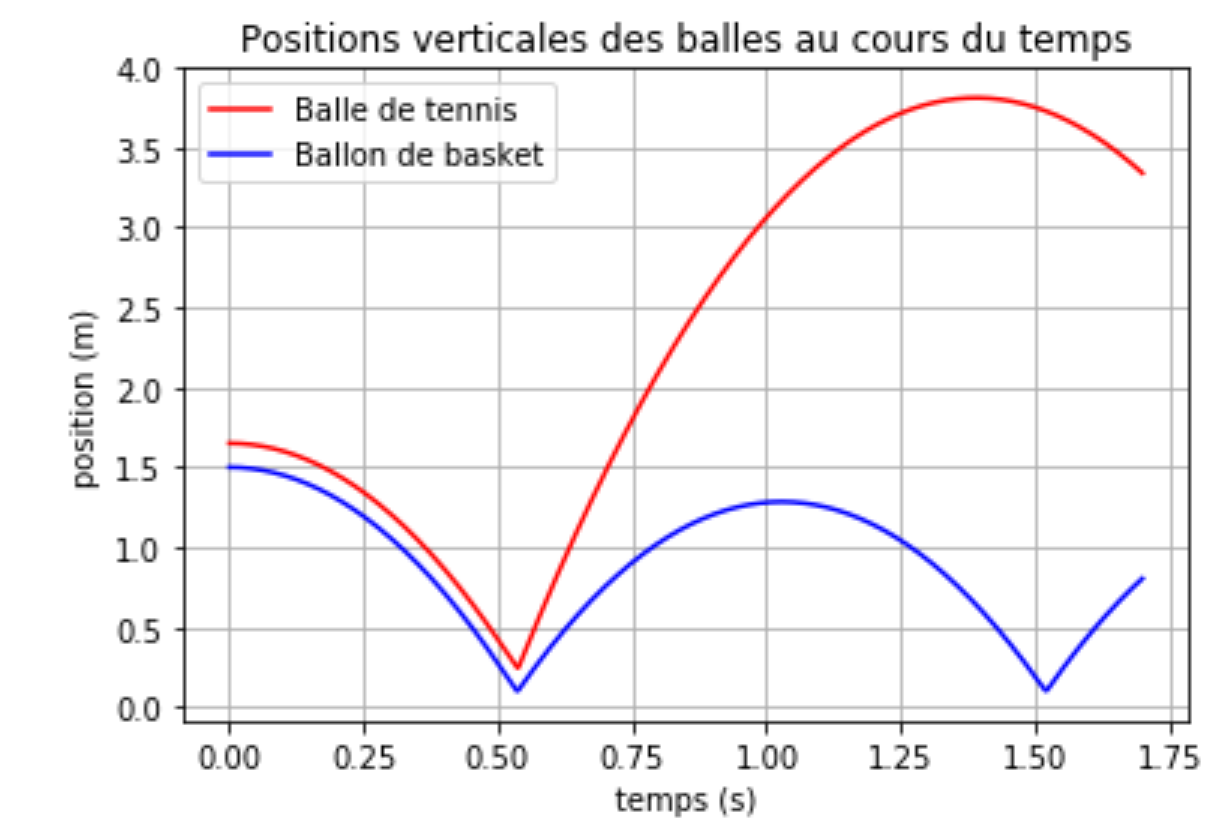
Le programme affiche le graphique, figure 10.

Figure 10.  Représentation graphique de la trajectoire de la balle de tennis (rouge) et du ballon de basket (bleu)

On retrouve, comme dans l'expérience, le tranfert d'énergie d'une balle à l'autre mis en évidence par le rebond beaucoup plus haut de la balle de tennis.

On trace aussi la représentation graphique des vitesses en fonction du temps, figure 11.

Figure 11.  Code python du tracé des vitesses des deux balles

Le programme affiche le graphique, figure 12.

Figure 12.  Représentation graphique des vitesses de la balle de tennis (rouge) et du ballon de basket (bleu)

Intéressons-nous maintenant uniquement à la balle de tennis et superposons la représentation graphique de sa vitesse et de sa position au cours du temps, figure 13.

Figure 13.  Code python du tracé de la vitesse et de la position de la balle de tennis

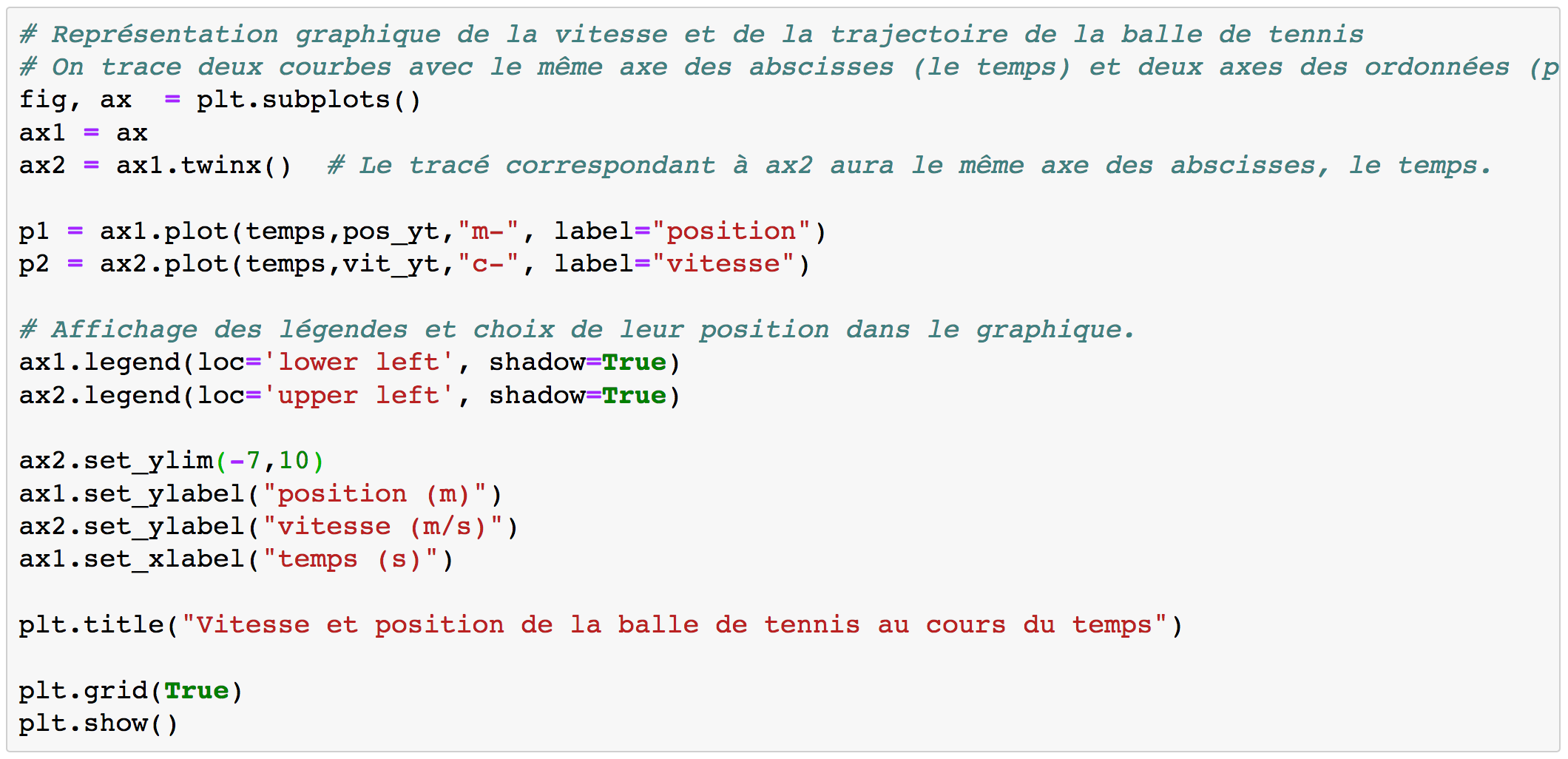
Le code est un peu différent car on va tracer deux courbes qui ont le même axe des abscisses (le temps) et deux axes des ordonnées différents (la vitesse en m/s et la position en m). À l'aide de la fonction twinx() on définit que l'axe des abscisses est le même pour les deux tracés.

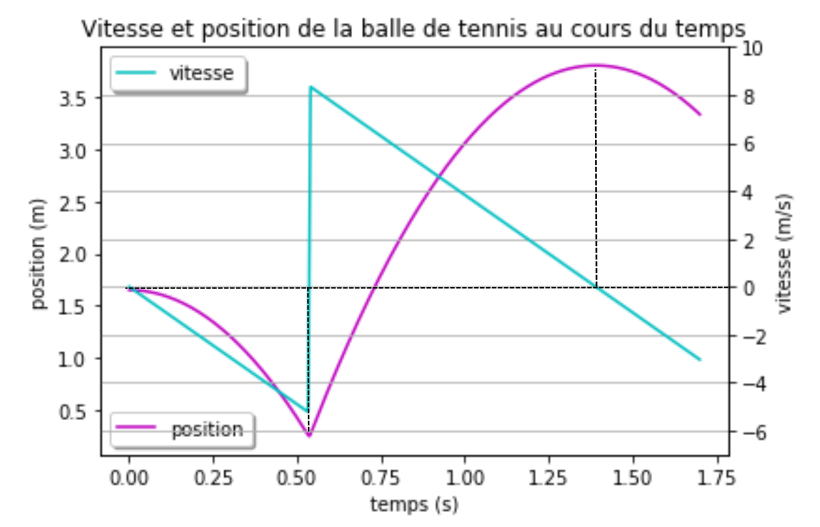
Le programme affiche le graphique, figure 14. Il est ensuite annoté ici par nos soins pour la discussion.

Figure 14.  Représentation graphique de la vitesse (cyan) et de la position (magenta) de la balle de tennis

On retrouve que lorsque la vitesse est nulle, la position de la balle de tennis est à un extremum de sa trajectoire, soit au point le plus bas : l'arrêt juste avant le rebond, soit au point le plus haut : l'arrêt juste avant la redescente.

Ensuite, on peut aussi retrouver l'accélération de pesanteur, par exemple, sur la première partie, encadrée en bleu, lorsque les balles sont en chute libre. On détermine tout d'abord l'indice du vecteur correspondant à la dernière position avant le rebond, figure 15.

Figure 15.  Détermination de l'accélération sur la première partie du mouvement (avant le rebond)

La fonction np.argmin() renvoie l'indice du vecteur correpondant à la valeur minimale de ce vecteur. En effet, la 10622^ème valeur du vecteur vitesse est de -5,2 ce qui correspond à la valeur minimale. De la même manière il existe la fonction np.argmax() qui renvoie, cette fois à l'indice du vecteur correpondant à sa valeur maximale.

Ensuite nous réalisons une régression linéaire des point calculés dans le vecteur vitesse, fonction que nous avons déjà rencontrée dans un article précédent « Analyse numérique appliquée à une source de tension, en langage Python ».

On calcule la régression sur les points correspondant à la première partie en chute libre de la balle de tennis, encadré en bleu sur la figure. Le calcul est donc réalisé pour les valeurs du vecteur vitesse dont l'indice est compris entre 0 et 10622.

Finalement,on retrouve bien une variation de vitesse, donc une accélération, égale à l'accélération de la gravité. On rappelle qu'ici nous ne prenons pas en compte les frottements.

On aurait pu tout aussi bien faire les calculs sur la deuxième partie du mouvement en chute libre.

On peut aussi comparer les variations de vitesses des deux balles, sur la figure 12. La pente est la même pour le ballon de basket et pour la balle de tennis ce qui permet de retrouver qu'en chute libre sans frottement, les corps tombent à la même vitesse, indépendamment de leur masse.

Intéressons-nous maintenant à l'énergie des balles.

Nous calculons les énergies cinétiques et potentielles des deux balles, figure 16.

Figure 16.  Code python pour le calcul des énergies cinétiques et potentielles des deux balles

Nous traçons l'énergie cinétique et potentielle de la balle de tennis, figure 17.

Figure 17.  Code python du tracé de l'énergie cinétique et potentielle de la balle de tennis

Le programme affiche le graphique, figure 18.

Figure 18.  Représentation graphique de l'énergie cinétique et potentielle de la balle de tennis

Si l'on s'intéresse à l'énergie cinétique, on retrouve qu'elle est, en effet, nulle au début de la trajectoire puis s'annule lorsque la balle touche le sol ou lorqu'elle est au sommet du rebond.

L'énergie potentielle suit bien la représentation de la position de la balle, au facteur masse fois gravité près.

On s'intéresse maintenant à l'énergie totale, c'est-à-dire à la somme de l'énergie cinétique et potentielle de la balle de tennis, figure 19.

Figure 19.  Code python du calcul de la somme des énergies cinétiques et potentielles de la balle de tennis

Le programme affiche le graphique, figure 20.

Figure 20.  Représentation graphique de la somme des énergies cinétiques et potentielles de la balle de tennis

On observe bien le transfert d'énergie qui a lieu au moment du rebond entre le ballon de basket et la balle de tennis. Si le système avait été isolé, l'énergie totale serait restée constante.

Traçons maintenant l'évolution de l'énergie du ballon de basket, figure 21.

Figure 21.  Code python du calcul de la somme des énergies cinétiques et potentielles du ballon de basket

Le programme affiche le graphique, figure 22.

Figure 22.  Représentation graphique de la somme des énergies cinétiques et potentielles du ballon de basket

Maintenant on va s'intéresser à l'énergie totale du système composé de la balle de tennis et du ballon de basket, figure 23.

Figure 23.  Code python du calcul de la somme des énergies cinétiques et potentielles du système

Le programme affiche le graphique, figure 24.

Figure 24.  Représentation graphique de la somme des énergies cinétiques et potentielles du ballon de basket

De manière rassurante, on constate que l'énergie totale du système est la même avant et après les rebonds. Nous n'avons, en effet, pas introduit de terme de dissipation dans la modélisation.

Par contre au moment des rebonds on observe deux pics, que l'on peut mettre en évidence en effectuant un zoom dans la représentation graphique, figure 25.

Figure 25.  Code python du zoom de la représentation graphique de la somme des énergies cinétiques et potentielles du système

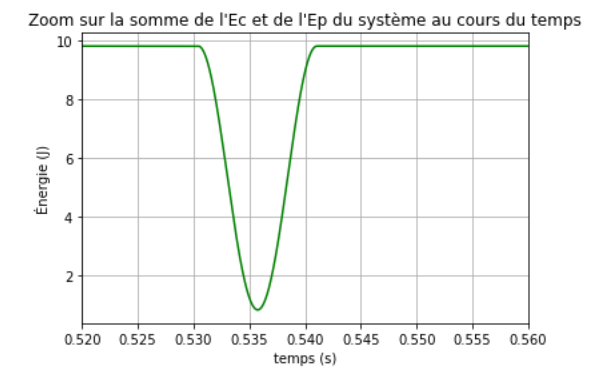
Le programme affiche le zoom sur le graphique au moment du premier rebond, figure 26.

Figure 26.  Zoom sur la représentation graphique de la somme des énergies cinétiques et potentielles du ballon de basket

On observe que pendant le rebond l'énergie n'est pas constante. Il s'agit tout simplement de l'énergie élastique des balles qui n'a pas été prise en compte dans le calcul de l'énergie totale : somme de l'énergie cinétique et de l'énergie potentielle.

Pour observer la conservation d'énergie mécanique du système, il faut simplement rajouter l'énergie élastique des balles aux moments des rebonds.

Pour modéliser les vecteurs ou les matrices, il est beaucoup plus simple d'utiliser le module numpy qui fournit le type array, plutôt que d'utiliser list. C'est une véritable atout pour les calculs numériques. Les opérations sur les tableaux (vecteurs ou matrices) sont optimisées avec numpy et sont beaucoup plus rapides qu'elles ne le seraient sur des listes équivalentes.

Par exemple, pour réaliser le calcul de l'énergie cinétique du ballon de basket avec les vitesses définies sous la forme de liste, il faut indiquer que chaque terme, appelé ici "v", de la liste [vitesse_yB] doit être mis au carré et multiplié par 0,5 et par la masse, figure 27.

Figure 27.  Code python du calcul de l'énergie cinétique avec utilisation delist et array