Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Diffraction à l'infini
11/09/2007
Résumé
Associer des figures de diffraction et des ouvertures diffractantes
Les images ci-dessous correspondent d'une part à des écrans diffractants et d'autre part à des figures diffractées. Chacune de celles-ci représente la répartition de l'intensité diffractée d'un des écrans dans les conditions de Fraunhofer (diffraction à l'infini). Les ouvertures diffractantes et les figures de diffraction sont montrées en négatif, les zones noires étant des régions éclairées.
Ces images ont été calculées numériquement à partir d'un logiciel de transformation de Fourier.
Il s'agit d'associer à chacune des ouvertures diffractantes - notées de a à j - les figures de diffraction - notées de 1 à 10. Si vous ne l'avez pas encore fait, nous vous invitons à chercher par vous-même les paires écran diffractant - figure diffractée, avant de regarder les réponses que vous trouverez ci-dessous.
L'intensité diffractée est proportionnelle au carré du module de la fonction transformée de Fourier de la transparence de l'écran diffractant. On en déduit les propriétés suivantes :
- La figure de diffraction a les mêmes symétries que l'écran diffractant ;
- Une fente fine horizontale diffracte la lumière dans une direction verticale ;
- Plus les dimensions de l'écran diffractant sont petites et plus la figure de diffraction est étalée ;
- Les interférences entre deux motifs identiques de l'écran diffractant se traduisent par des franges qui modulent l'intensité diffractée : la figure de diffraction ressemble à celle d'un motif seul et présente des zones éclairées et sombres en alternance. L'écart entre ces franges est inversement proportionnel à la distance entre les motifs.
Ces propriétés, qui sont très fortement liées à celles de la transformée de Fourier, nous guident pour trouver les bonnes associations. Nous présentons les écrans dans le même ordre que dans la page « cherchez les paires », et les figures diffractées correspondantes en dessous, en rappelant leur numéro.
Commençons par des écrans de formes variées :
Ecran diffractant a |
Ecran diffractant b |
Ecran diffractant c |
Ecran diffractant d |
Figure diffractée 4 |
Figure diffractée 1 |
Figure diffractée 2 |
Figure diffractée 3 |
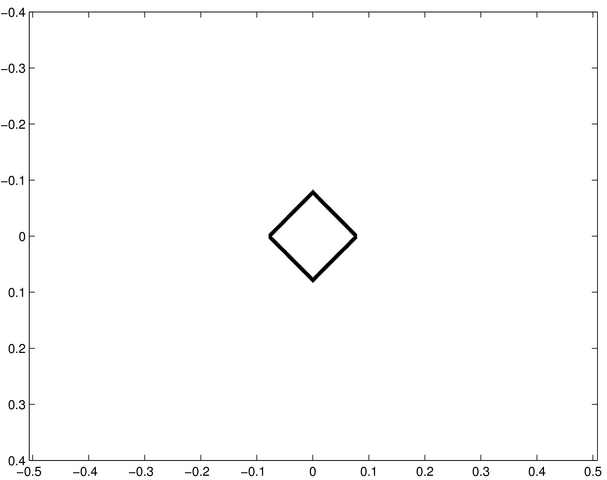
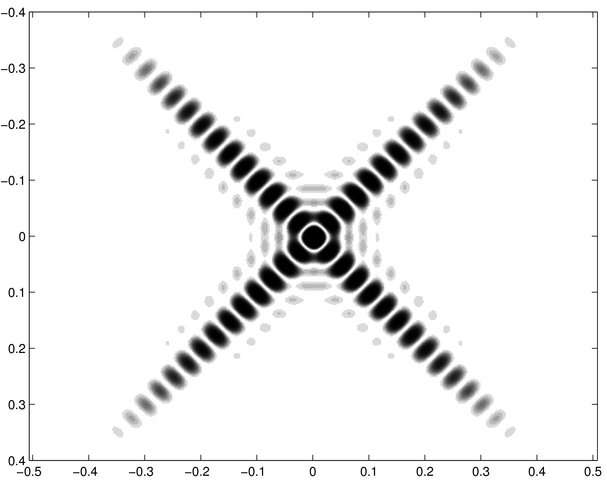
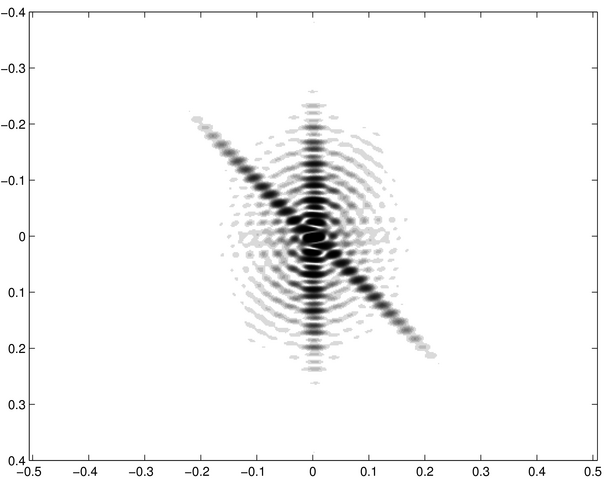
Les traits fins du losange diffractent des taches larges dans deux directions perpendiculaires. Elles sont modulées par des franges fines d'interférence dues aux couples de segments parallèles. C'est équivalent à deux systèmes de fentes d'Young disposés selon deux directions perpendiculaires. En dehors des axes principaux de la figure diffractée, on observe des structures plus faibles ; elles sont dues d'une part à la longueur finie de chaque segment du losange, et d'autre part à des interférences entre les ondes diffractées par les segments contigus. | Les deux axes de la figure diffractée correspondent aux deux segments du chiffre trois. Les anneaux sont diffractés par la partie circulaire. | Les deux figures sont invariantes par rotation d'un angle de 90°. Chaque segment de la croix diffracte comme une fente fine dans la direction perpendiculaire. En dehors de ces deux taches larges alignées sur deux axes, on observe un quadrillage de structures étroites dues à des interférences entre les ondes diffractées par chacun des segments et à leur longueur finie (comme en a-4). | Chaque cercle du chiffre huit diffracte des anneaux (comme en h-9). Les deux systèmes d'anneaux sont concentriques (cf. le théorème de Babinet concernant la translation de l'écran diffractant). Les franges horizontales fines sont l'effet d'interférences entre les deux ondes diffractées par chacun des cercles. |
Poursuivons avec une série de fentes :
Ecran diffractant e |
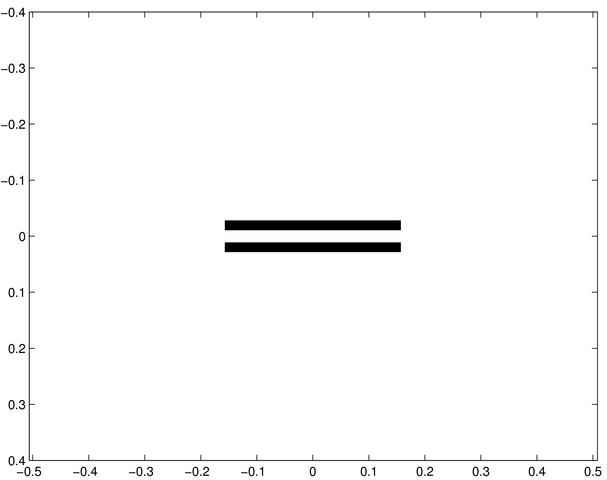
Ecran diffractant f |
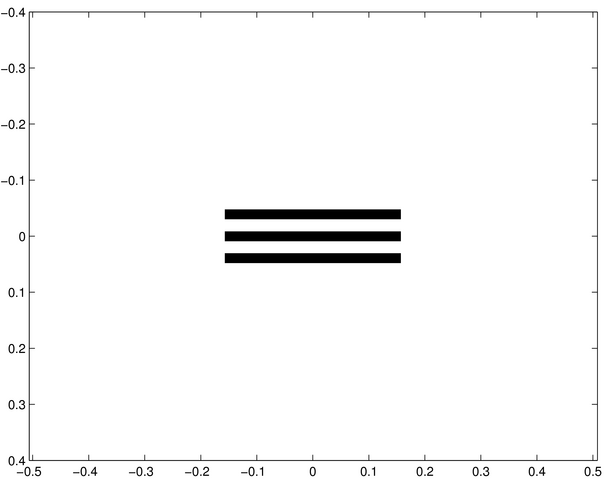
Ecran diffractant g |
Figure diffractée 6 |
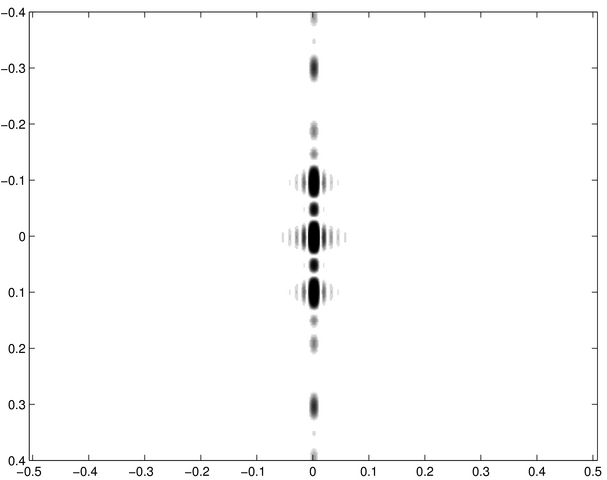
Figure diffractée 7 |
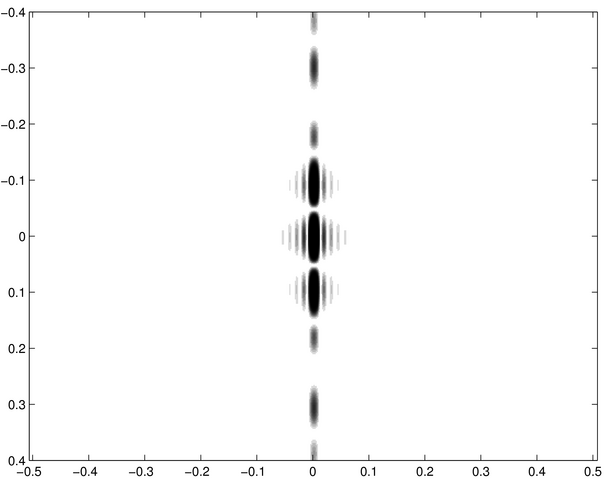
Figure diffractée 5 |
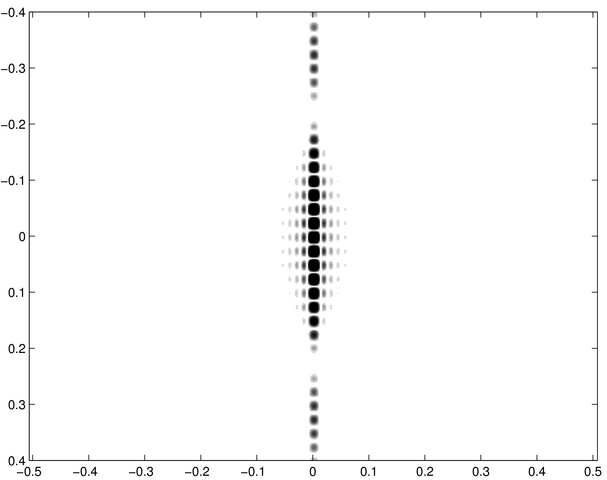
Les trois fentes constituent un réseau élémentaire dont le « pas » est égal à l'écart des fentes d'Young f-7 ci-contre. On vérifie que la distance entre les maxima principaux diffractés par ce réseau est égale à l'interfrange de f-7. | C'est une figure classique de diffraction par des fentes d'Young. L'écart entre les fentes est environ le double de la largeur de chacune, ce qui explique que le premier minimum de diffraction (celui de l'enveloppe large) se situe à environ deux interfranges du centre. Les faibles structures de part et d'autre de l'axe principal de diffraction sont dues à la longueur finie des fentes d'où la présence de diffraction dans une direction parallèle aux fentes. | C'est une figure de diffraction de fentes d'Young, analogue à f-7, avec des fentes plus écartées d'un facteur 4 environ, d'où un interfrange d'autant plus faible. Il y a maintenant environ 8 franges d'interférences entre le centre de la figure et le premier minimum de diffraction. |
Enfin des écrans de formes circulaires :
Ecran diffractant h |
Ecran diffractant i |
Ecran diffractant j |
Figure diffractée 9 |
Figure diffractée 10 |
Figure diffractée 8 |
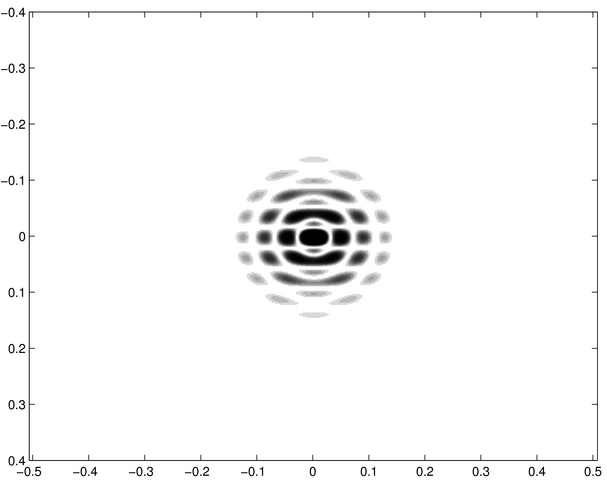
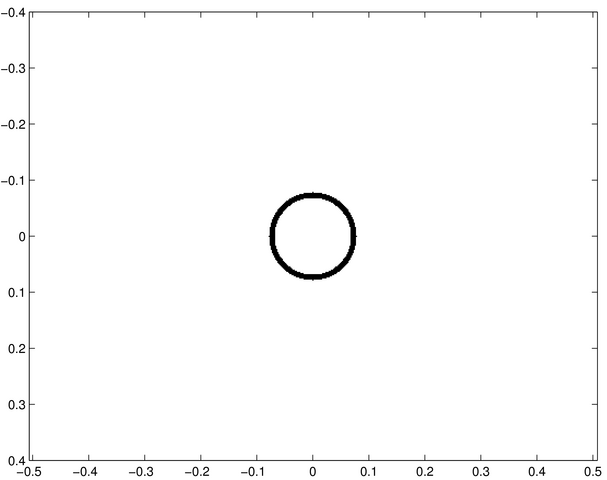
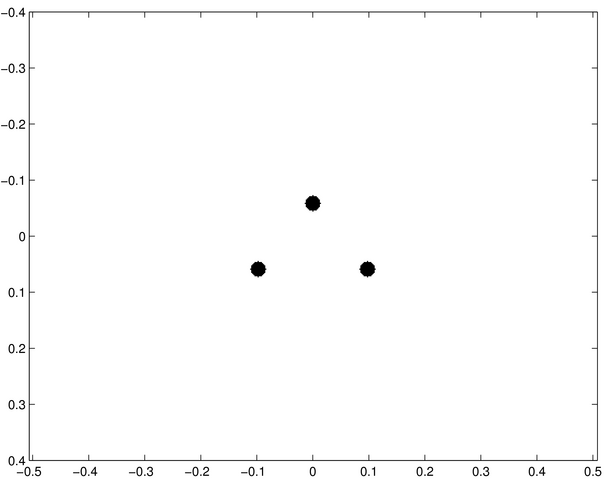
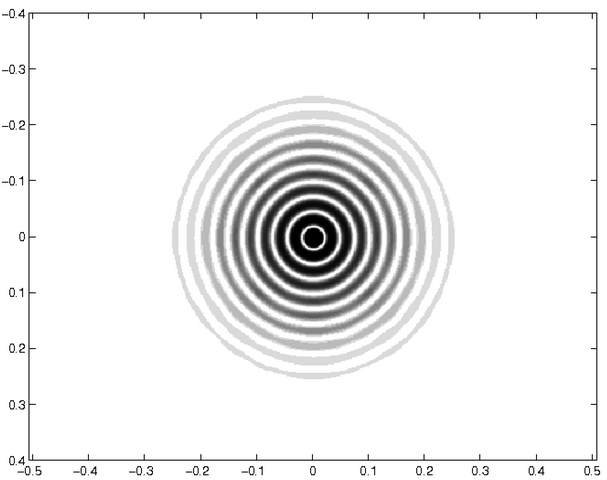
L'écran est de symétrie circulaire ; la figure diffractée est un système d'anneaux similaire à celui diffracté par un trou circulaire. | La structure large en anneaux est celle diffractée par chacun des trois petit trous circulaires. Elle est modulée par des structures fines réparties selon trois axes correspondant aux interférences entre les ondes diffractées par chacun des trous. | Les figures sont analogues à celles de i-10. Les trous diffractants ont un diamètre environ quatre fois plus grand. On observe des anneaux d'un diamètre réduit d'un facteur quatre, avec une modulation fine similaire. |
Pour citer cet article :
Diffraction à l'infini, Catherine Simand, Marie-Christine Artru, septembre 2007. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/QSfigurediffractionSol.xml