Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Diffraction à l'infini
26/06/2007
Résumé
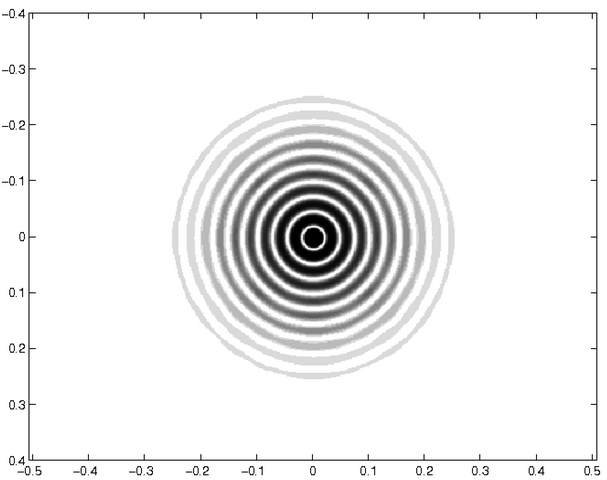
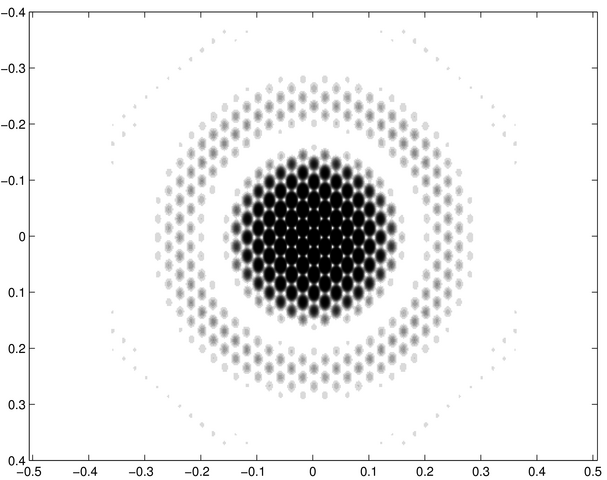
Saurez-vous associer à chaque figure de diffraction l'ouverture diffractante correspondante ?
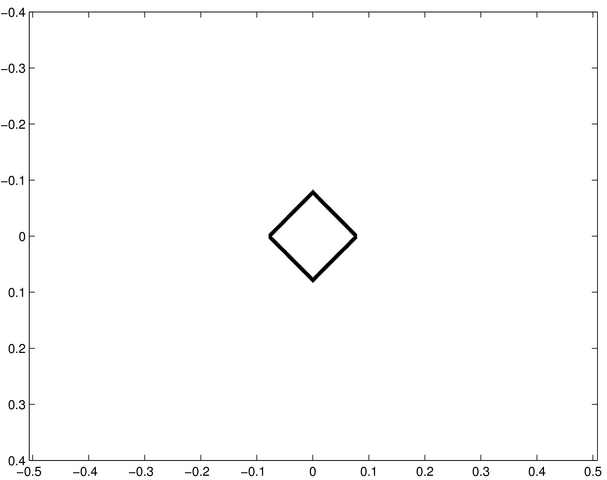
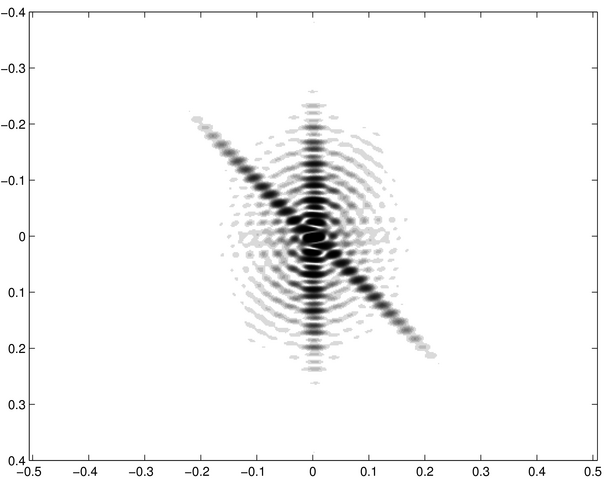
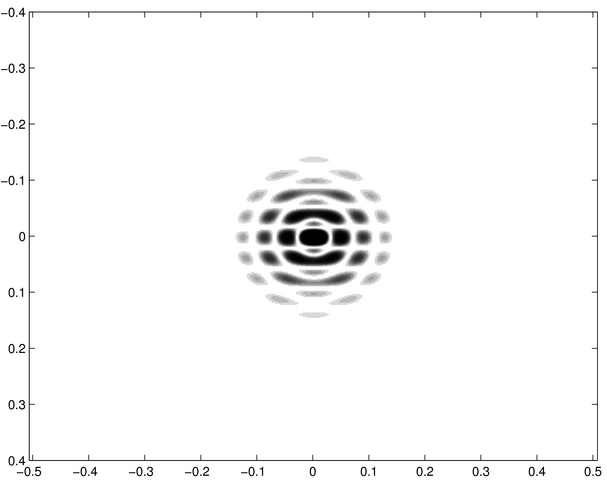
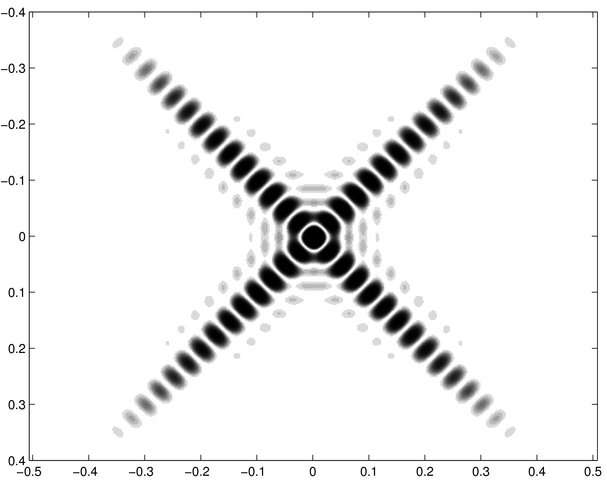
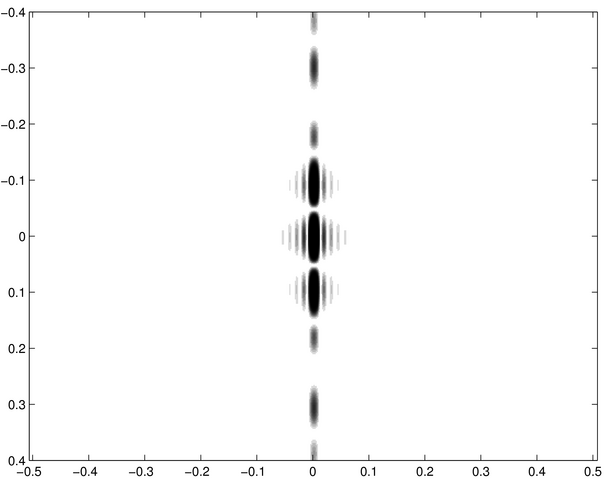
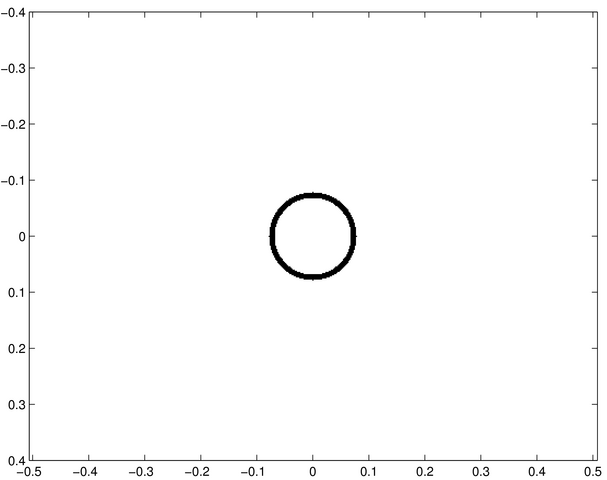
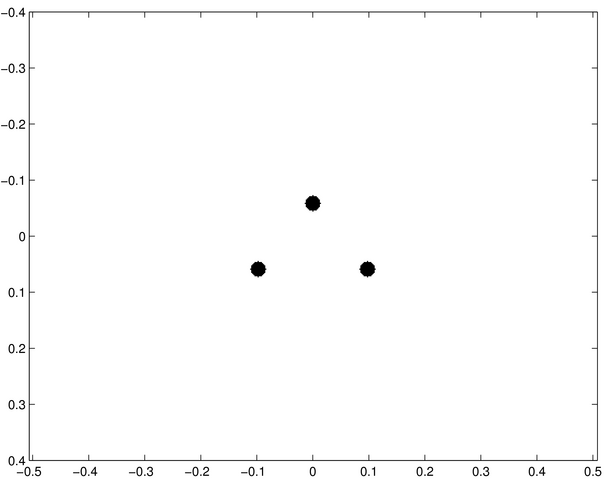
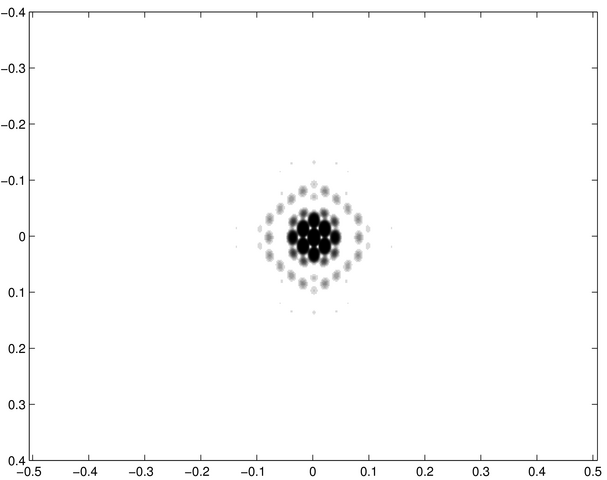
Les images ci-dessous correspondent d'une part à des écrans diffractants et d'autre part à des figures diffractées. Chacune de celles-ci représente la répartition de l'intensité diffractée d'un des écrans dans les conditions de Fraunhofer (diffraction à l'infini). Les ouvertures diffractantes et les figures de diffraction sont montrées en négatif, les zones noires étant des régions éclairées.
Ces images ont été calculées numériquement à partir d'un logiciel de transformation de Fourier.
Saurez-vous associer à chacune des ouvertures diffractantes - notées de a à j - les figures de diffraction - notées de 1 à 10 ?
Commençons par des écrans de formes variées :
|
|
|
|
Ecran diffractant a | Ecran diffractant b | Ecran diffractant c | Ecran diffractant d |
|
|
|
|
Figure diffractée 1 | Figure diffractée 2 | Figure diffractée 3 | Figure diffractée 4 |
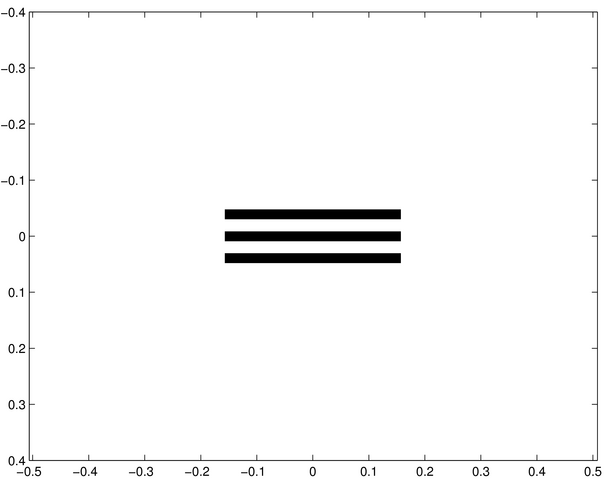
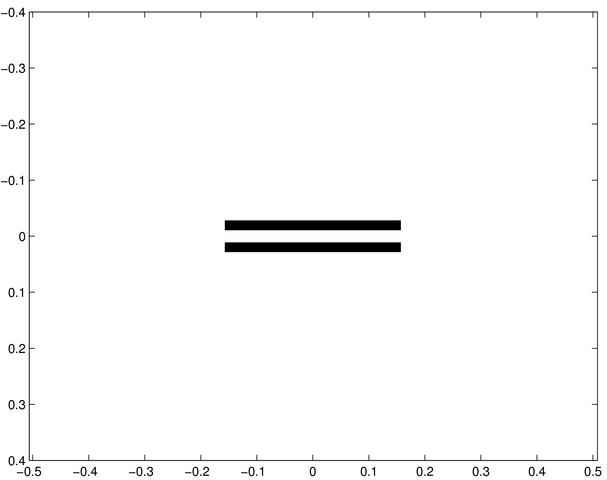
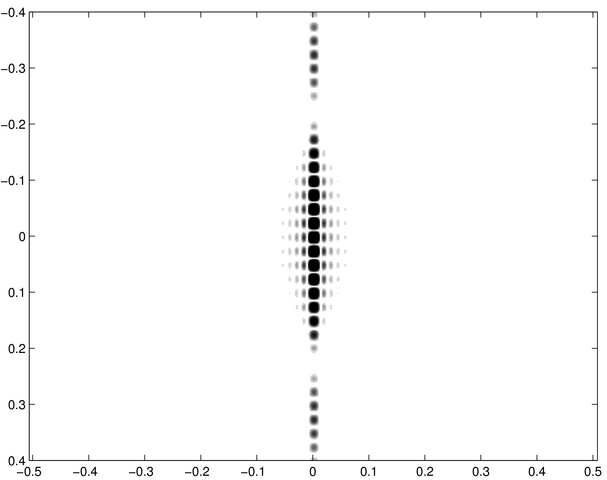
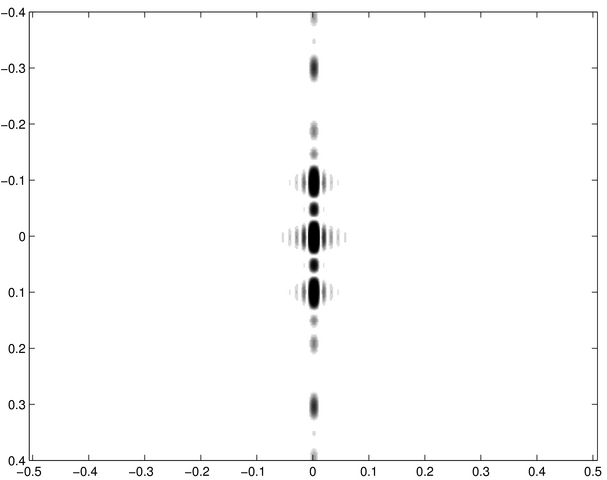
Poursuivons avec une série de fentes :
|
|
|
Ecran diffractant e | Ecran diffractant f | Ecran diffractant g |
|
|
|
Figure diffractée 5 | Figure diffractée 6 | Figure diffractée 7 |
Enfin des écrans de formes circulaires :
|
|
|
Ecran diffractant h | Ecran diffractant i | Ecran diffractant j |
|
|
|
Figure diffractée 8 | Figure diffractée 9 | Figure diffractée 10 |
Avez vous trouvé les bonnes associations écran diffractant - figure diffractée ? Toutes les réponses ici !
Pour citer cet article :
Diffraction à l'infini, Catherine Simand, juin 2007. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/QSfigurediffraction.xml