Activer le mode zen
Ressource au format PDF
Classification
Indices optiques : dérivation à partir des équations de Maxwell, signification physique, expression
12/09/2003
Résumé
À partir des équations de Maxwell dans le vide et dans un milieu matériel, on dérive les formules de l'indice optique n puis on décrit la signification physique de la partie réelle et de la partie imaginaire de n. Enfin, pour quelques milieux particuliers, on détermine des expressions approchées de n. Un article du dossier « La vitesse de la lumière », proposé par Gabrielle Bonnet.
Table des matières
Indices optiques : dérivation à partir des équations de Maxwell
Soit une onde électromagnétique plane et monochromatique de pulsation ω = 2 π / T (T période temporelle de l'onde) et de vecteur d'onde k orienté suivant le sens de propagation de l'onde et de norme k = 2 π / λ (λ longueur d'onde). On note le champ électrique (complexe) de cette onde Eω(r,t) et son champ magnétique Bω(r,t), ces champs étant exprimés au point r. Ils ont l'expression suivante * :
Eω(r,t) = E0 ei (k.r - ω t) | et | Bω(r,t) = B0 ei (k.r - ω t) |
i est le nombre complexe, souvent noté j en physique, tel que i2 = -1. On a préfèré la notation i dans les équations qui suivent afin d'éviter les confusions avec la densité de courant j
k.r est le produit scalaire des vecteurs k et r
Lorsque l'onde se propage dans le vide, on retrouve aisément (cf paragraphe 1.1. qui suit), à partir des équations de Maxwell, la relation : ω/k = c où c = 299.792.458 m/s est la vitesse de la lumière dans le vide. Lorsque l'onde se propage dans un milieu matériel, cependant, cette relation n'est plus valable. L'onde est diffusée par les atomes qu'elle rencontre et sa propagation est ralentie. On définit alors (cf paragraphe 2) l'indice n du milieu comme n = k c/ω où n est une fonction, a priori complexe, de la variable ω. On verra aussi comment n est relié à la vitesse de propagation de l'onde.
On montre, dans un milieu isolant de susceptibilité magnétique nulle (c'est-à-dire où la perméabilité magnétique relative μr = 1) que
n = √‾εr |
où εr est la permittivité électrique relative du milieu.
n vérifie aussi la relation n = c B0/E0.
Ondes électromagnétiques dans le vide
« Ondes électromagnétiques dans le vide » : on montre comment, dans le vide, on peut déduire des équations de Maxwell que la vitesse de l'onde lumineuse vaut c.
Ondes électromagnétiques dans un milieu
« Ondes électromagnétiques dans un milieu » : on donne les équations de Maxwell dans un milieu matériel après avoir rappelé brièvement l'origine de ces équations puis on démontre la relation n = √‾εr... Si vous êtes rebuté par les équations, passez directement au paragraphe suivant !
Signification physique de l'indice n(ω)
On rappelle que, pour une onde électromagnétique monochromatique de pulsation ω, le champ électrique Eω s'écrit :
Eω(r,t) = E0 ei (k.r - ω t) |
et que l'indice n(ω) du milieu est défini par la relation
ω/k = c/n(ω) |
L'indice n(ω) est a priori un nombre complexe que l'on peut écrire n(ω) = n'(ω) + i n"(ω) avec n' et n" réels.
Si n(ω) n'est pas réel (n" ≠ 0), alors il en est de même pour k = ω/c n(ω) que l'on peut décomposer en partie réelle et partie imaginaire : k = k' + i k" = ω/c (n' + i n")
D'une façon générale, Eω se réécrit :
Eω(r,t) = E0 ei (k'.r - ω t) e- k".r |
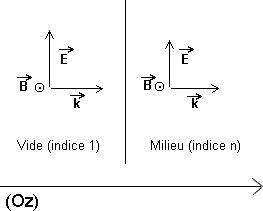
Supposons, pour fixer les idées, que k est colinéaire à (Oz). On considère une onde électromagnétique issue du vide et pénétrant dans le milieu. L'expression de Eω(r) à l'intérieur du milieu matériel comprend un terme exponentiellement décroissant avec z (pour peu que k" soit positif) :
e- k" z = e- ω n" z / c |
et un terme périodique :
ei (k' z - ω t) = ei (ω n' z / c - ω t) = ei ω n'/c (z - t c/n') |
L'étude de ces deux termes permet de comprendre la signification physique de n' et n".
Partie imaginaire n" de l'indice n(ω)
Le premier terme, exponentiellement décroissant et correspondant à la partie imaginaire de l'indice, montre que Eω(r) est absorbée sur une longueur d de l'ordre de c/(n"ω) = λ/(2n"π) donc de l'ordre de λ/n" où λ est la longueur d'onde de l'onde considérée. L'onde électromagnétique de fréquence ω est donc absorbée sur une longueur inversement proportionnelle à la partie imaginaire de l'indice du milieu. Plus cette partie imaginaire est faible, et plus l'atténuation de l'onde se fait lentement.
Si l'indice n est réel, ceci signifie que l'onde électromagnétique traverse le milieu sans être absorbée : le milieu est transparent pour cette longueur d'onde.
Partie réelle n' de l'indice n(ω)
Le terme périodique montre que la partie réelle de n(ω) détermine la vitesse de phase vφ de l'onde :
vφ = ω/k'(ω) = c/n'(ω) |
Si l'indice n est réel, alors n' = n et on retrouve la relation que l'on écrit généralement lorsqu'on s'intéresse à un milieu transparent pour les longueurs d'ondes considérées : vφ = c/n(ω).
Valeur de l'indice d'un milieu
Il existe un certain nombre de modèles permettant de donner une valeur approchée, tout au moins sous certaines conditions, de l'indice d'un milieu. En fait, même si certains modèles classiques existent, ces formules doivent, de façon rigoureuse, s'établir dans le cadre de la mécanique quantique. Ces calculs sortent du cadre de cet article et nous souhaitons seulement rappeler les résultats obtenus.
On va considérer un milieu matériel isotrope, homogène, non ferroélectrique ou ferromagnétique, non supraconducteur et transparent dans le domaine des fréquences visibles (l'indice n(ω) est alors réel pour toutes les longueurs d'onde comprises entre 450 nm et 750 nm environ).Ceci signifie qu'il n'y a pas de raie ni de bande d'absorption dans cette gamme de fréquence, par contre il y a des raies d'absorption en-dehors du visible et on appellera ωi les pulsations correspondant à des raies (ou des bandes) d'absorption situées dans l'ultraviolet (UV), dans l'infrarouge (IR) ou au-delà.
On a alors, pour un milieu dense, la formule approchée suivante, qui permet de relier une grandeur macroscopique, l'indice du milieu, aux propriétés microscopiques de la matière :
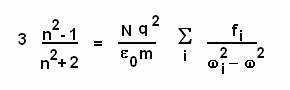
avec n : indice du milieu (pour la pulsation ω considérée), ωi : pulsation correspondant à une raie d'absorption des molécules composant le milieu, N densité de molécules présentes dans le milieu, et q et m, charge et masse de l'électron. Les coefficients fi sont quant à eux des nombres sans dimension, appelés « force d'oscillateur », de somme égale au nombre d'électrons de l'atome (ces forces d'oscillateur s'écrivent en fonction d'éléments de matrices qui sortent du calcul quantique de la susceptibilité moléculaire).
Si le milieu est très peu dense on a :
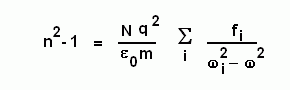
On constate sur ces formules que, pour un même milieu, dont on fait seulement varier la densité, la différence n2 - 1 (ou (n2 - 1)/(n2 + 2) pour un milieu dense) est proportionnelle à la densité du milieu. Pour des milieux de natures différentes, par contre, la densité n'est pas seule en jeu puisqu'il faut connaître les fréquences d'absorption du milieu pour déterminer son indice.
De nombreuses expressions approchées de l'indice d'un milieu ont été trouvées, souvent à l'aide de modèles purement classiques. Pour en savoir plus on peut se référer aux manuels d'introduction à l'électromagnétisme de Licence ou de classe préparatoire aux grandes écoles (comme les livres de Bertin, Renault et Faroux, en particulier "Electromagnétisme 4") au moins pour les explications classiques, ou à un cours plus avancé pour les calculs de mécanique quantique.
Article suivant : « Relativité et vitesse de la lumière ».
Article précédent : « Historique : de Galilée à nos jours, évolution de la notion de vitesse de la lumière ».
Dossier : « La vitesse de la lumière ».
Pour citer cet article :
Indices optiques : dérivation à partir des équations de Maxwell, signification physique, expression, Gabrielle Bonnet, septembre 2003. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Indice.xml




