Activer le mode zen
Ressource au format PDF
Classification
La durée du crépuscule est-elle la même sous toutes les latitudes ?
14/02/2006
Résumé
Qu'est-ce qui détermine la durée du crépuscule ?
Table des matières
La durée du crépuscule est-elle la même sous toutes les latitudes ? Est-elle la même en toutes saisons ?

Crépuscule sur les romarins dans le sud de la France...
Figure 1.
La réponse :
Qu'est-ce qui détermine la durée du crépuscule ?
Le crépuscule "perçu" correspond à une certaine luminosité, qui persiste alors même que le soleil est couché. Cette luminosité dépend de deux choses :
- de l'angle que font les rayons du soleil par rapport à l'horizon. Cet angle peut se calculer facilement en fonction de la saison et de la latitude de l'observateur.
- des conditions atmosphériques. Même en excluant les temps nuageux, le taux d'humidité, ou de poussières, dans l'air, a une incidence sur la luminosité qui sera perçue par un observateur extérieur, pour un angle donné. Sur une planète sans atmosphère, il n'y a pas de crépuscule mais un passage instantané de la lumière à l'obscurité.
On peut définir un crépuscule "formel" : le crépuscule est ainsi conventionnellement considéré comme durant du coucher du soleil au moment où celui-ci fait un angle γ donné au-dessous de l'horizon. Cette définition ne tient pas compte des conditions atmosphériques (variables de jour en jour). Le crépuscule dit "civil" correspond à γ = 6°
Durée du crépuscule "formel" en fonction de la latitude et de la saison
On définit ici le crépuscule comme correspondant à l'intervalle de temps pendant lequel le soleil se trouve entre son coucher et l'angle γ en-dessous de l'horizon. On rappelle que γ = 6° pour le crépuscule dit "civil".
La durée du crépuscule peut se calculer par exemple en suivant ces deux étapes :
- calcul de θ, l'angle que font, à la date considérée, les rayons du soleil arrivant sur Terre et l'axe de rotation de la Terre.
- calcul, en fonction de θ et de la latitude λ de l'observateur, du temps que passe l'observateur dans la zone de luminosité crépusculaire
Première étape : calcul de l'angle θ entre les rayons du soleil et l'axe de la Terre
Pour ce calcul plaçons-nous dans le référentiel de Copernic, dans un repère u, v, w.
w définit la perpendiculaire au plan de l'écliptique, et l'axe de la Terre appartient au plan défini par les vecteurs u et w (voir figure ci-dessous).
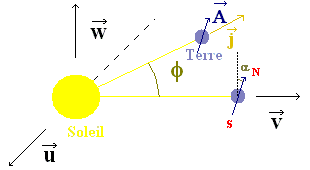
La Terre est représentée au solstice d'hiver (l'axe Soleil-Terre est alors coliénaire à v) et à une autre date. A est le vecteur unitaire colinéaire à l'axe de rotation de notre planète.
Figure 2.
- α est l'angle que fait l'axe de la Terre (fixe dans ce référentiel) avec le vecteur w, on a α = 23,45°
- φ est l'angle que fait l'axe Soleil-Terre avec le vecteur v, on a φ = 2 π t/TA, avec t = 0 au solstice d'hiver et TA = 1 an
On montre alors que le vecteur unitaire j colinéaire avec l'axe Soleil-Terre et dirigé dans la direction Soleil-Terre a pour expression j = v cos φ - u sin φ, et que le vecteur unitaire A colinéaire à l'axe de la Terre et orienté du pôle Sud vers le pôle Nord a pour expression A = w cos α + v sin α.
On a cos θ = j.A, on obtient donc l'expression :
cos θ = cos φ sin α |
Calcul de la durée du crépuscule en fonction de θ et de la latitude
Pour ce calcul (que nous ne détaillerons pas en entier), il peut être plus pertinent de se placer dans le repère (i, j, w), où j est le vecteur défini au paragraphe précédent, colinéaire à la direction Soleil-Terre, w est perpendiculaire au plan de l'écliptique comme indiqué dans le paragraphe précédent, et enfin, i, qui complète le repère orthonormé, est perpendiculaire aux deux autres vecteurs et appartient au plan de l'écliptique.

Figure 3.
Si M est le point d'observation, situé à la latitude λ,
et R le rayon de la Terre, on peut trouver facilement, dans ce repère
:
- l'équation du cercle correspondant au coucher du Soleil (les points de ce cercle vérifient y=0)
- l'équation du cercle correspondant à la fin du crépuscule (les points de ce cercle vérifient y= R cos γ)
- l'équation du cercle, centré sur l'axe de rotation de la Terre, que décrit M au cours d'une journée : on a x = R cos ω cos λ, y = R sin λ cos θ - R cos λ sin ω sin θ et z = R sin λ sin θ + R cos λ sin ω cos θ sachant que ω est un paramètre angulaire décrit la position de M sur le cercle
De ces équations on tire que la durée du crépuscule T vaut :
T = 1 jour × (ω1 - ω0)/2π
ω1 et ω0 étant définis par :
sin ω0 = tan λ / tan θ
sin ω1 = - sin γ /(cos λ sin θ) + tan λ / tan θ
Ces expressions peuvent sembler peu parlantes tant qu'on n'en tire pas un certain nombre de règles générales et qu'on ne les applique pas à des exemples concrets...
Des crépuscules de durées variées
On montre, dans le cas général, que le crépuscule est d'autant plus court, à date donnée, que l'on se rapproche de l'équateur.
Enfin, on constate aussi qu'il y a une dissymétrie entre le solstice d'été et le solstice d'hiver, faible pour de basses latitudes, mais importante lorsqu'on se rapproche des pôles...
Quelques exemples de durées du crépuscule civil selon les latitudes et les saisons :
Latitude (localisation) | Crépuscule au solstice d'hiver | Crépuscule en été | Crépuscule aux équinoxes |
60°N (pointe de l'Ecosse) | 1,14 h | 1,97 h | 0,80 h |
45°N (France) | 0,66 h | 0,72 h | 0,57 h |
15°N (Sénégal) | 0,45 h | 0,46 h | 0,41 h |
0° (Equateur) | 0,44 h | 0,44 h | 0,40 h |
13°S (Wallis et Futuna) | 0,45 h | 0,45 h | 0,41 h |
A tout ceci, il ne faut pas oublier d'ajouter que le crépuscule que nous percevons effectivement dépend aussi des conditions atmosphériques, beaucoup moins quantifiables que la latitude ou la date, mais dont le rôle est essentiel...
Pour citer cet article :
La durée du crépuscule est-elle la même sous toutes les latitudes ?, Gabrielle Bonnet, février 2006. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/QScrepuscule.xml




