Mirages dans l’Univers – quand la gravité nous joue des tours

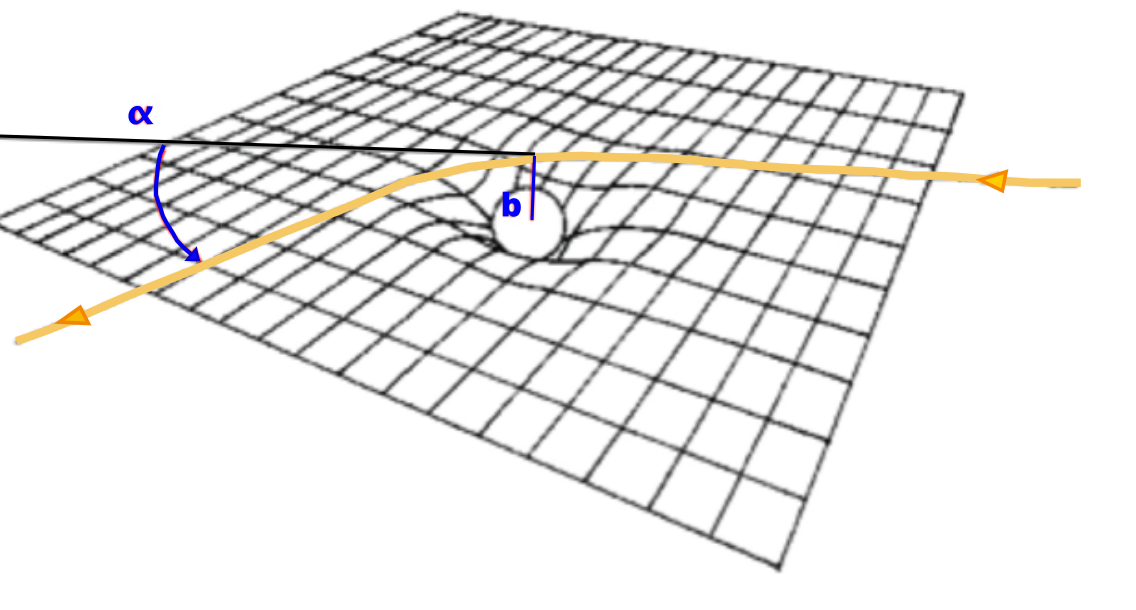
La théorie de la Relativité Générale d’Einstein explique la gravitation comme une déformation de l’espace au voisinage des objets massifs (Figure 1). Une des prédictions de cette théorie, découverte dès 1912, est qu’un rayon lumineux provenant d’une source astrophysique et passant à proximité de cet objet massif va suivre cette déformation et son trajet ne sera plus rectiligne : il subira un changement d’orientation, ou déflexion, d’un petit angle α dont la valeur dépendra de la masse M de l’objet, de la vitesse de la lumière c et du paramètre d’impact du rayon lumineux b :

$\alpha =4\genfrac{}{}{0.1ex}{}{GM}{c^{2}b}$

Figure 1. Illustration de la déformation de l’espace autour d’une masse et de l’influence sur le trajet d’un rayon lumineux

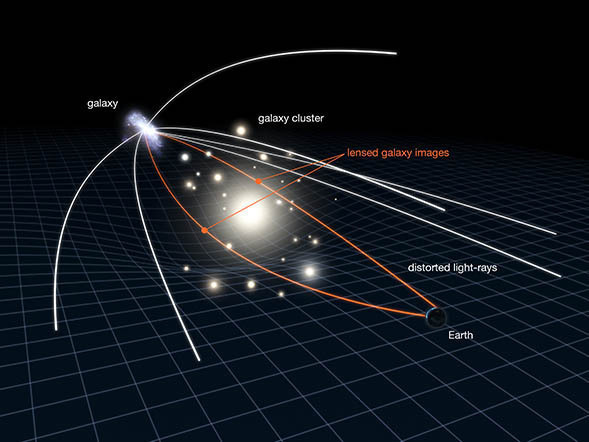
Même si cet effet se produit dans le vide, il s’apparente, sous sa forme et dans les équations, à la déflexion d’un rayon lumineux dans une lentille convergente. Pour cette raison, on parle souvent de « lentille gravitationnelle ». Dans les cas les plus extrêmes, la déformation est telle que les rayons lumineux peuvent prendre plusieurs chemins pour arriver jusqu’à un observateur, qui voit alors un « mirage » avec plusieurs images de la même source (Figure 2).

Figure 2. Effet de mirage gravitationnel : la lumière d’une galaxie distante prend deux trajets différents (en rouge) pour atteindre la Terre. © NASA, ESA and L. Calcada

Par le calcul, le soleil s’avère alors une lentille gravitationnelle suffisamment forte pour que son effet sur la lumière issue d’étoiles distantes soit mesurable. En effet, en utilisant la masse du soleil M = 2.10³⁰ kg et un paramètre d’impact b = 6,95.10⁸ m au bord du soleil, on trouve un angle α = 1,75” (secondes d’arc). On s’attend donc à voir les étoiles au voisinage du soleil s’en écarter d’un angle α. Cette valeur est, déjà en 1912, suffisamment grande pour être mesurable par de petits télescopes.

L’astronome anglais Sir Arthur Eddington (1882-1944), célèbre observateur de l’époque, propose de confirmer cette prédiction d’Einstein. Mais comment mesurer des étoiles de faible luminosité en plein jour près du soleil ? Pendant une éclipse ! Il profite d’une éclipse de soleil prévue en 1919 et lance une expédition sur l’île de Principe, au large des côtes de l’Afrique, pour mesurer la position des étoiles proches du soleil. En comparant des plaques photographiques des mêmes étoiles prises en l’absence de soleil quelques mois auparavant, il pourra prouver qu’elles se sont déplacées sur le ciel de la valeur précisément prédite par la Relativité Générale ! Ce résultat propulsa Einstein et sa théorie sur le devant de la scène.

Au delà du soleil, le phénomène de déflexion est apparu trop faible pour être mesurable, et tout ceci aurait pu rester comme une simple bizarrerie de la Relativité Générale. Cependant, dans les années 1930, l’astronome Fritz Zwicky (1898-1974) montre que les galaxies et les amas de galaxies, beaucoup plus massifs que les étoiles, produiraient un effet de lentille gravitationnel impressionnant : jusqu’à plusieurs dizaines de secondes d’arcs de déflexion ! Mais la faiblesse des galaxies et la difficulté d’avoir un alignement parfait entre deux objets n’ont pas permis une telle observation avant les années 1980.

En 1979, l’observation d’un premier mirage gravitationnel, sous la forme d’un « quasar double », confirme ces prédictions. En 1987, c’est la découverte des premiers arcs gravitationnels autour des amas de galaxies les plus massifs. Ces observations ont été facilitées par l’arrivée des premiers détecteurs ultra-sensibles, combinés avec des télescopes de diamètres toujours plus grands. Le champ de recherche des lentilles gravitationnelles a depuis connu un nouveau rebond avec l’avènement du télescope spatial Hubble en 1991, et sa qualité d’image exceptionnelle.

La première notion que nous pouvons illustrer est l’effet de déflexion des rayons lumineux. Pour cela, on peut représenter l’influence gravitationnelle d’un objet sur un espace à deux dimensions. Nous utilisons : un grand drap résistant (une taille de 2 x 2 m est suffisante), un objet lourd que l’on place au centre, et une balle légère (ou une bille) lancée en ligne droite sur le drap. Lorsque le drap est tendu en hauteur ; le poids central va le déformer et illustrer (par analogie) la courbure de l’espace autour d’un objet massif. On peut ainsi comparer la trajectoire de la bille (représentant un rayon lumineux) en présence ou non de l’objet massif : l’effet de courbure de l’espace (le drap) va dévier la trajectoire du photon (la bille) au lieu de le laisser se propager en ligne droite (Figure 4 en haut).

Figure 4. Expériences pratiques - (Haut) Mise en évidence de la courbure de l’espace avec un drap tendu. (Bas) Observations d’images obtenues au travers d’une lentille fabriquée à partir d’un verre à pied

Une deuxième expérience utilise les propriétés de déformation des rayons lumineux qui sont identiques à celles d’une lentille en verre. Il est en effet possible de fabriquer une « lentille » avec un profil de verre reproduisant (de manière approximative) l’effet d’un corps massif sur une source d’arrière-plan. Le profil correspondant est très proche de celui de la partie inférieure d’un verre à pied (figure 4a). Nous avons ainsi coupé et limé les pieds de plusieurs verres pour un plus grand confort d’utilisation.

En observant une source ponctuelle ou une grille régulière tracée sur une feuille de papier au travers d’une de ces lentilles de verre on arrive très facilement à reproduire les effets visuels d’une lentille gravitationnelle, en particulier :

On peut retrouver par le calcul la masse d’un amas de galaxies à partir des observations astrophysiques obtenues à l’aide du télescope spatial Hubble. Les amas de galaxies sont les structures les plus massives de l’Univers qui forment un système lié par la gravitation. On y trouve donc de nombreux effets de lentille gravitationnelle, et parmi les plus spectaculaires (Figure 5).

Figure 5. Observation de l’amas de galaxies Abell 2218 et mesure de la distance R_arc d’un arc gravitationnel (d’une couleur orangée) au centre de l’amas

À partir de la position d’un grand arc gravitationnel identifié dans les images d’amas de galaxies à une distance R_arc du centre (ici la galaxie de l’amas la plus brillante), il est possible de remonter à la masse M (<R_arc) qui correspond à la masse totale contenue dans un cercle (représenté en clignotement figure 5) centré sur l’amas et tangent à cet arc, en appliquant une équation simplifiée.

$M(<R_{arc})=\genfrac{}{}{0.1ex}{}{c^2}{4G}\genfrac{}{}{0.1ex}{}{D_{OS}}{D_{LS}{D}_{OL}}{R}_{arc}^2$

Avec c la vitesse de la lumière et G la constante de la gravitation universelle. Les valeurs D_OL, D_LS et D_OS correspondent aux distances de l’observateur à la lentille, de la lentille à la source, et de l’observateur à la source respectivement.

En prenant des valeurs typiques pour un amas sité à 2 millards d'années lumière de l'observateur (D_OL = 2.10⁹ al), une source lumineuse distante de 5 milliards d’années lumière de l'observateur (D_OS = 5.10⁹ al), D_LS = D_OS - D_OL, et un arc de longueur de 300 000 années lumière (R_arc = 3.10⁵ al), on trouve une masse M ~ 2,5.10⁴⁴ kg, c'est-à-dire environ 120 000 milliards de masses solaires (M_S ~ 2.10³⁰ kg).

Le résultat obtenu, en milliards de fois la masse du Soleil, peut être (en moyenne) divisé par 100 pour trouver l’équivalent en nombre de galaxies, une galaxie contenant environ 100 milliards de fois la masse du Soleil. Bien entendu nous travaillons ici avec des hypothèses simplificatrices (distribution de matière symétrique…) et des ordres de grandeur. On aboutit alors à une masse de 1 200 galaxies environ.

On peut alors comparer ce résultat aux observations : dans le même cercle pour lequel est estimée la masse, on n’observe qu’une à plusieurs dizaines de galaxies. La grande différence entre ces deux valeurs correspond en effet à la présence de matière noire, qui n’apparaît pas dans les observations sous forme lumineuse mais dont l’effet influence la position des arcs gravitationnels.