Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
L'expérience CMS au LHC
12/09/2022
Article paru dans le « Journal de physique et de chimie des étudiants » du département Sciences de la Matière de l'ENS de Lyon, janvier 2022.
Résumé
L'objectif de cet article est de présenter la reconstruction et l'étude des particules à l'aide du détecteur Compact Muon Solenoid (CMS) installé au Large Hadron Collider (LHC) du CERN (laboratoire de l'organisation européenne pour la recherche nucléaire), près de Genève.
Table des matières
Introduction
Le LHC est un accélérateur de particules utilisé pour générer des collisions à haute énergie entre différentes entités. Dans cet article, nous aborderons d'abord de façon générale son histoire et son fonctionnement, pour nous concentrer par la suite sur le détecteur CMS (Compact Muon Solenoid). Les différents sous-détecteurs le composant seront présentés ainsi que la méthode de « reconstuction » de particules traversant CMS. Enfin, nous nous pencherons sur l'étude des particules non observables directement par le détecteur avec l'exemple du boson de Higgs. En effet, les particules issues des collisions ne sont pas toutes stables, certaines se désintègrent avant d'entrer dans les parties sensibles du détecteur. Ce sont alors leurs produits de désintégration qui sont observés. L'enjeu est donc de relier les propriétés des particules mesurées à celles qui ne le sont pas, ce que nous illustrerons à partir d'une étude de la collaboration CMS : A measurement of the Higgs boson mass in the diphoton decay channel.
1. Le LHC
1.1 L'histoire du LHC
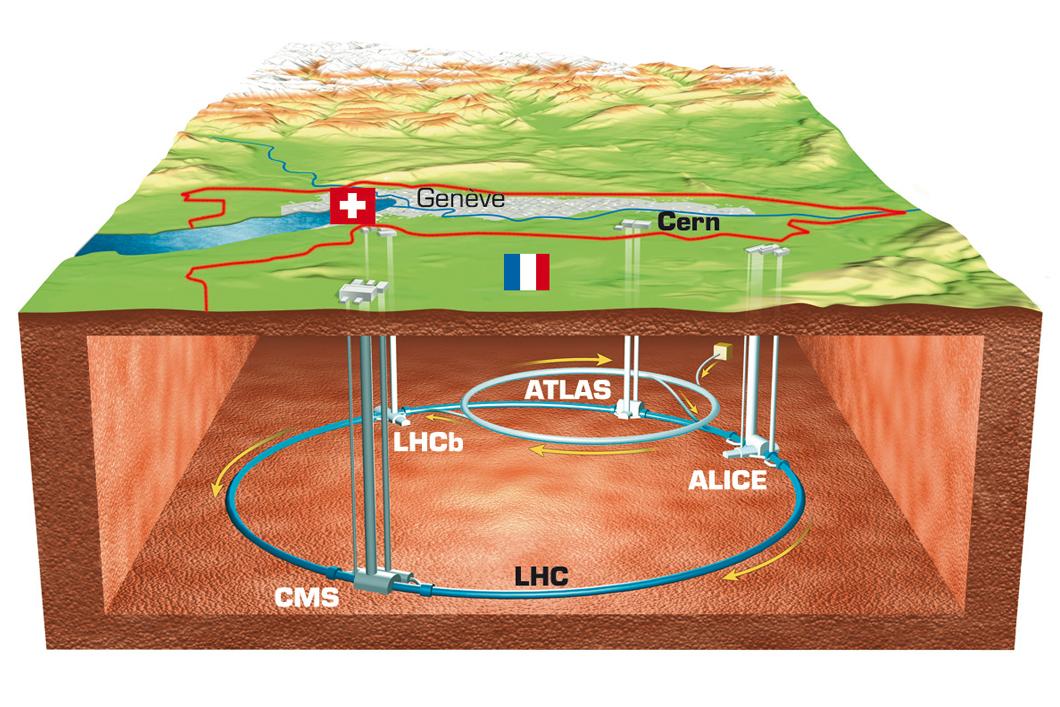
Le LHC (Large Hadron Collider) est un accélérateur de particules circulaire de 27 km de circonférence, situé entre 50 et 100 m de profondeur sous la frontière franco-suisse comme illustré sur la figure 1. Il permet de réaliser des collisions proton-proton, proton-ion lourd et ion lourd-ion lourd. Il a été mis en service en 2008, puis amélioré en 2015. L'une de ses grandes ambitions était de permettre la découverte du boson de Higgs, chose faite en 2012 par les collaborations ATLAS et CMS. Il constitue toujours un outil extrêmement important dans l'exploration des différentes théories de la physique des particules allant de celle du modèle standard à la théorie des cordes. Ce projet regroupe plus de 10 000 scientifiques de plus de 100 nationalités.
1.2 Fontionnement général
L'objectif du LHC est de faire entrer des particules en collision à des vitesses proches de celle de la lumière. L'énergie de collision est convertie en masse, cette dernière correspondant à de nouvelles particules. L'accélération des hadrons[1] (protons en particulier) se fait grâce à des électro-aimants créant un champ électromagnétique. Le champ électrique permet de donner de l'énergie cinétique aux particules. Ce sont des champs magnétiques d'au plus 8 T, soit près de 200 000 fois le champ magnétique terrestre, qui courberont leurs trajectoires.
Les champs électromagnétiques générés permettent aux protons d'atteindre une vitesse de 99,999% de la vitesse de la lumière et donc de grandes énergies (près de 6,5 TeV). Les deux faisceaux de particules circulant en sens opposé sont créés grâce à un processus d'accélération se décomposant en plusieurs étapes : une préaccélération par un accélérateur linéaire (LINAC2 pour les protons et LINAC3 pour les ions lourds) et une série d'accélérateurs circulaires (les synchrotrons) pour finalement atteindre une énergie de 450 GeV par particule, puis injection dans le LHC où les particules atteindront 6,5 TeV grâce à un champ électrique. La vidéo figure 2 présente l'accélération des particules.
Figure 2. Présentation de la source et de l'accélération des particules Source : Meet Linac4, CERN [2]. |
En même temps, plus d'un millier d'aimants dipolaires courbent les trajectoires des particules tout en limitant les pertes d'énergie. Le faisceau est également concentré par des aimants quadripolaires. Enfin, les deux faisceaux de particules sont focalisés à l'aide d'un champ magnétique pour augmenter les probabilités de collision. Ces aimants (figure 3) ont une taille de l'ordre de la dizaine de mètres et nécessitent d'être refroidis à très basse température. Les bobines de ces aimants sont parcourues par plus de 10 000 A. Ainsi, 96 tonnes d'hélium superfluide permettent de maintenir le réseau d'aimant à 1,9 K afin de permettre l'utilisation de matériaux supraconducteurs pour éviter les surchauffes par effet Joule.
Figure 3. Coupe 3D d'un électroaimant dans le LHC Source : LHC image gallery, CERN [2]. |
Enfin arrivent les collisions, créant de nouvelles particules, qui seront détectées indirectement. En effet, parmi ces nouvelles particules, certaines sont instables et se décomposent donc rapidement. Ce sont les particules issues de cette décomposition qui sont détectées et analysées par le détecteur installé autour du point de collision. Les quatre principaux détecteurs de particules du LHC sont ATLAS, ALICE, CMS et LHCb (figure 1).
Nous allons dans la suite nous concentrer sur CMS, dont une photo se trouve en figure 4 et une vidéo figure 5.
Figure 4. Photographie du détecteur CMS, prise de l'extérieur Source : LHC rocks the seesaw model, CERN [2]. |
Figure 5. Présentation du détecteur CMS Source : CMS footage for social media, CERN [2]. |
2. Le détecteur CMS
Le détecteur CMS a été conçu dans le but premier de découvrir le boson de Higgs et d'étudier la brisure de symétrie électrofaible [3]. Son design généraliste lui permet toutefois d'être exploité pour de nombreuses autres analyses. Il permet de détecter les photons, les électrons, les hadrons neutres et chargés, ainsi que les muons. Le détecteur ATLAS, également généraliste, utilise des technologies et un design différent de CMS. Bien que leurs objectifs soient communs, cela permet de consolider leurs résultats respectifs.
2.1 Structure générale et caractéristiques
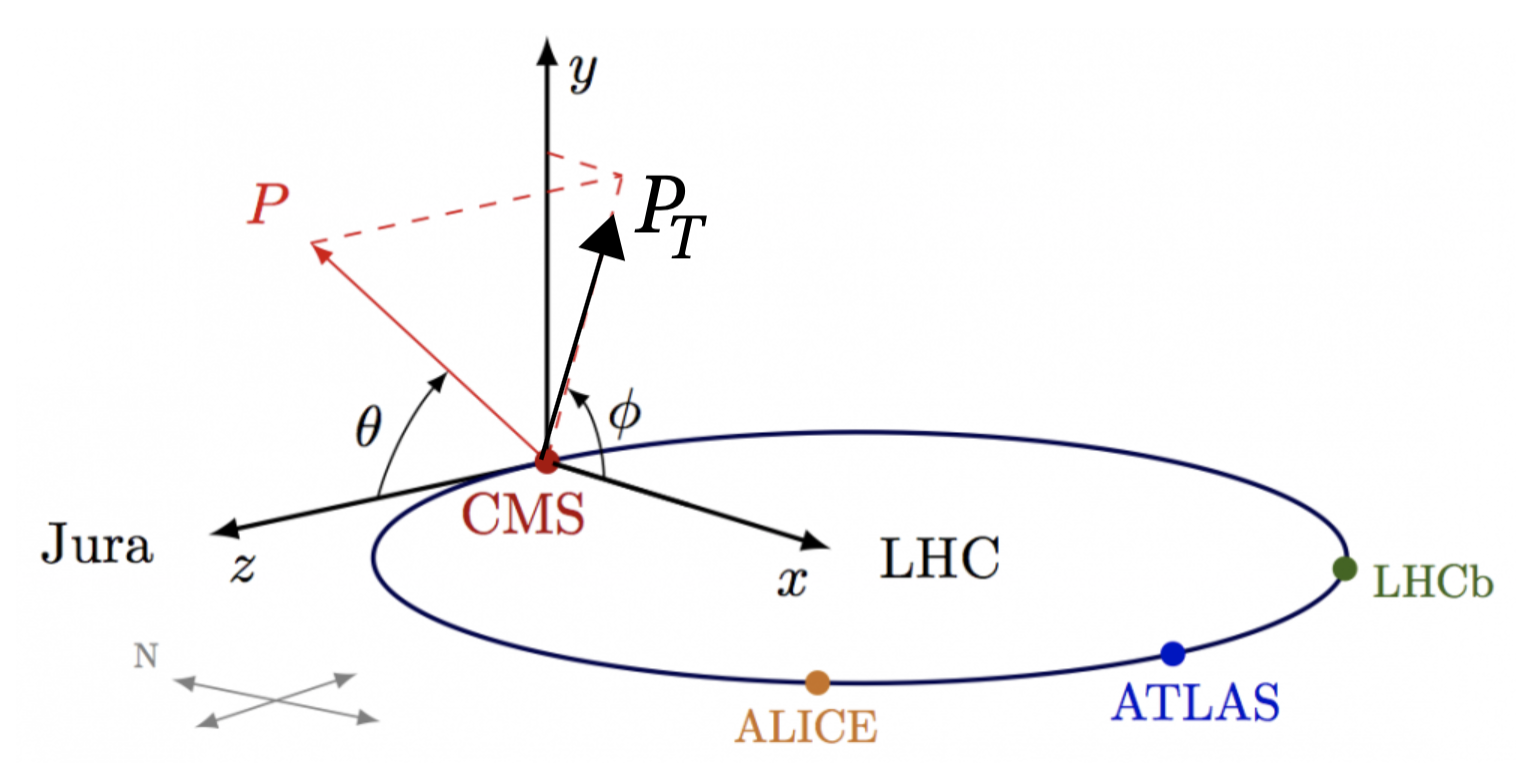
Le centre du détecteur CMS est traversé par les particules suffisamment stables pour ne pas se désintégrer pendant le trajet entre le point de collision et l'entrée dans ce sous-détecteur. Ces particules sont issues des collisions et des désintégrations des autres particules instables. De plus, chaque partie de CMS est dédiée à l'étude de certains types de particules. Nous allons dans la suite donner une brève description de chacun de ces éléments, après avoir défini quelques paramètres importants. Pour ce faire, appuyons-nous sur la figure 6.
La quantité de mouvement \(p\) est une grandeur conservée mais la phénoménologie des collisions de protons ne permet pas de connaitre sa projection \(p_z\) sur l'axe du faisceau dans l'état initial, c'est-à-dire avant la collision. Toutefois, on peut se servir de l'impulsion, dans le plan (\(xy\)) transverse à l'axe du faisceau, \(p_T\) qui est nulle dans l'état initial. Cependant, certaines particules (comme les neutrinos) n'interagissent pas avec le détecteur. L'énergie liée à ces particules n'est donc pas détectée mais la conservation de l'impulsion nous permet de déterminer cette énergie manquante dans le plan transverse. L'énergie transverse manquante est alors définie comme la somme des quantités de mouvement dans le plan transverse des particules visibles et doit correspondre à l'impulsion transverse totale des particules indétectables. Par conséquent, la quantité de mouvement transverse \(p_T\) et l'énergie transverse \(E_T\) sont des grandeurs intéressantes pour lier les particules détectées à celle dont elles proviennent, créées lors de la collision. Ces deux quantités sont définies respectivement comme suit [3] :
$$ p_T=\sqrt{p_x^2+p_y^2} $$
$$ E_T = E \sin \theta $$
avec \(p_x\) et \(p_y\) les impulsions suivant les axes \(x\) et \(y\) des particules.
La pseudo-rapidité est une coordonnée spatiale décrivant l'angle de la trajectoire d'une particule par rapport à l'axe du faisceau. Cette nouvelle coordonnée est adaptée aux interprétations relativistes, ce qui en fait une description couramment utilisée en physique des particules. On définit la pseudo-rapidité \(\eta\) par :
$$ \eta = - \ln \Big( \tan \frac{\theta}{2} \Big) $$
Figure 6. Schéma du système de coordonées de CMS. L'origine du repère est le point de collision Source : CMS footage for social media, CERN [2]. |
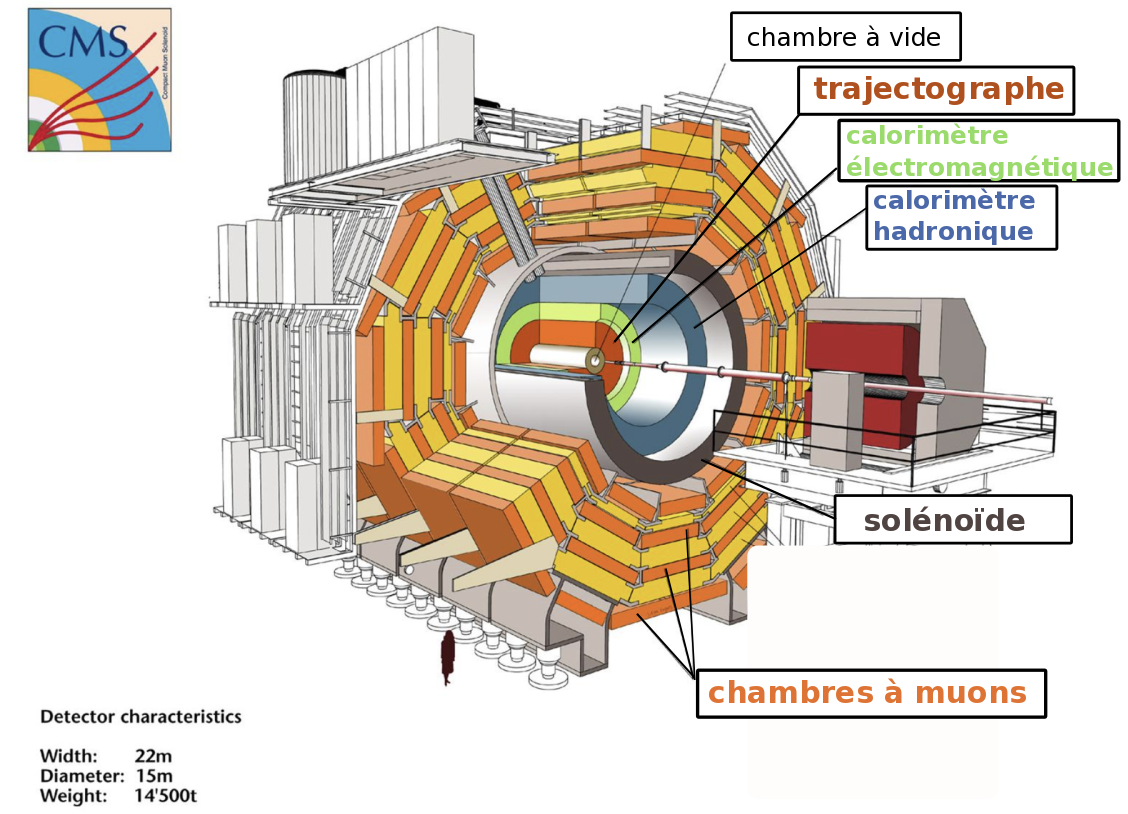
Le détecteur CMS possède une forme cylindrique de 28,7 m de long, de 15 m de diamètre, et pèse plus de 14 000 t. L'ensemble du détecteur s'articule autour d'un aimant solénoïde supraconducteur. Notons qu'il est le seul des quatre détecteurs du LHC à avoir été construit à la surface, puis assemblé sous terre. Sa structure générale est schématisée en figure 7. CMS est constitué de 5 sous-détecteurs. En partant du centre où ont lieu les collisions de particules vers l'extérieur se trouvent successivement : un trajectographe, un calorimètre électromagnétique, un calorimètre hadronique, un solénoïde supraconducteur et des chambres à muons.
Figure 7. Schéma du détecteur CMS Source : LHC image gallery, CERN [2]. |
Détaillons maintenant plus en détail les différentes fonctions des éléments constituant le détecteur CMS.
2.2 Trajectographe
Le trajectographe (au centre, en orange sur la figure 7) a une forme cylindrique de 5,8 m de long pour 2,5 m de diamètre. Il entoure le point de collision des particules et est principalement composé de plusieurs couches de silicium. Comme le montre la figure 7, il est le premier sous-détecteur rencontré par les particules. Son objectif est de reconstruire les trajectoires des particules chargées et donc d'obtenir leur charge. Son rôle est primordial car c'est grâce à cette estimation que l'on obtient celle de l'impulsion de la particule détectée. Par conséquent, la détermination des trajectoires se doit d'être efficace et précise.
2.3 Calorimètre électromagnétiaque ou ECAL
Comme vu précédemment, le trajectographe permet de savoir si la particule possède une charge, si oui laquelle et d'estimer \(p_T\). Or \(p_T\) ne correspond pas à l'énergie totale. Par conséquent, un nouvel élément est nécessaire pour estimer cette énergie : les calorimètres. L'ECAL (en vert, figure 7) se charge de l'estimation de l'énergie totale des photons et des électrons par un processus destructif. Plus précisement, l'ECAL cylindrique est composé de cristaux scintillants d'oxyde de tungstate de plomb PbWO4 (dont une image est proposée en figure 8) et de détecteurs de pied de gerbe. Ces derniers sont des surfaces de silicium permettant de déterminer si un photon incident est isolé ou si c'est une paire de photons très rapprochés.
Figure 8. Photographie du module équipé de cristaux scintillants de PbWO4 Source : Chatrchyan et al., J. Journal of Instrumentation 2008, 3. |
L'oxyde de tungstate de plomb a une grande densité (8,29 g.cm-3) et permet au calorimètre électromagnétique d'avoir une réponse rapide tout en résistant efficacement aux radiations. De plus, la longueur de radiation des cristaux est faible. Cette longueur est la distance parcourue par un électron de haute énergie dans la matière jusqu'à perdre environ 60% de son énergie. Cela permet donc aux cristaux d'arrêter les particules sur de courtes distances. L'énergie des photons et des électrons est recueillie grâce au phénomène de scintillation : la particule traversant les cristaux émet de la lumière, proportionnelle à son énergie. Des photodiodes à avalanche ont pour objectif de recueillir cette lumière. Notons que la lumière en sortie des cristaux dépend fortement de la température (perte de 2,1% d'intensité lumineuse par degré à 18°C), d'où l'importance des systèmes de refroidissement. De plus, les cristaux perdent de leur transparence avec le temps. Des recalibrations sont donc régulièrement effectuées par laser.
2.4 Calorimètre hadronique ou HCAL
L'objectif de ce calorimètre est le même que le précédent mais la mesure d'énergie se fait pour les hadrons (chargés et neutres). Le HCAL (en bleu, figure 7) est constitué d'une alternance de couches d'absorbeurs en laiton et de scintillateurs. Comme précédemment, ce sont ces derniers qui mesurent l'énergie des hadrons incidents par scintillation. Toutefois, la lumière est ici recueillie par des fibres optiques. Le laiton est utilisé pour sa transparence aux muons, qui ne sont pas perturbés avant l'arrivé dans les chambres à muons.
2.5 Aimant solénoïde
Cet aimant solénoïde (cylindre gris sur la figure 7) mesure 12,5 m de long pour 6,5 m de diamètre. Avec un courant d'intensité nominale de 19,14 kA, il génère un champ magnétique de 3,8 T. L'ensemble du solénoïde est maintenu à 1,9 K par un système de refroidissement à l'hélium.
Ce champ magnétique très intense permet de courber la trajectoire des particules électriquement chargées. Par exemple, la trajectoire d'un électron sera déviée tandis que celle d'un photon ne le sera pas. De plus, le sens de déviation de la trajectoire d'une particule chargée dépend de son signe. Augmenter la courbure de la trajectoire revient à diminuer le rayon de courbure r défini comme :
$$ r=\frac{p_T}{qB} $$
Où \(p_T\) est l'impulsion de la particule, \(q\) sa charge et \(B\) la norme du champ magnétique.
2.6 Chambre à muons
À ce stade du détecteur, les muons sont les seules particules qui n'ont pas été absorbées. Elles sont détectées à l'intérieur des chambres à muons (en orange, figure 7). Ces chambres utilisent des détecteurs à gaz, permettant d'estimer \(p_T\) à 2% près pour des muons de moins de 200 GeV.
3. Reconstruction de particules observables
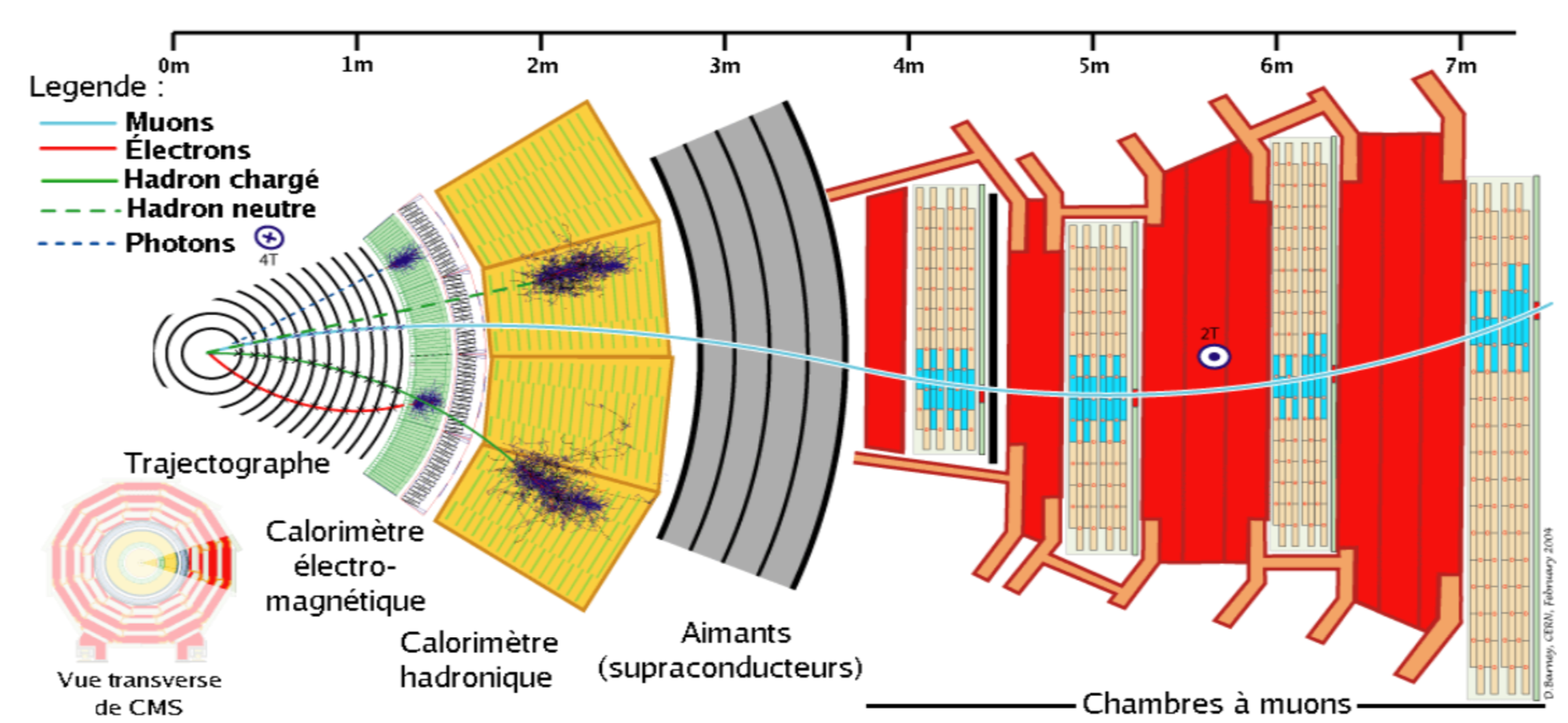
Nous avons donc vu la composition du détecteur CMS et le rôle de chaque composant dans la mesure des grandeurs pertinentes pour les particules détectées. Mais comment sont-elles observées ? À vrai dire, elles ne sont pas réellement « observées », seules les traces laissées lors de la traversée du détecteur sont accessibles. Ces traces sont les signaux de leur passage. Il faut donc, avec les signaux enregistrés, « reconstruire » ces particules. Les particules de nature différente ont des comportements distincts au sein du détecteur. De plus, chaque sous-détecteur joue un rôle précis pour chaque type de particule. Ceci est illustré en figure 9.
Tout d'abord, les particules chargées laissent une trace dans le trajectographe. Le champ magnétique va dévier leur trajectoire selon un rayon de courbure \(r\). Une déviation est donc caractéristique des électrons (trait rouge plein), des hadrons chargés (trait vert plein) et des muons (trait bleu plein). Une trajectoire non déviée appartiendra donc aux particules sans chage. Puis vient le calorimètre électromagnétique, où les photons et les électrons laissent une trace sous forme d'énergie comme vu dans la section intitulée « 2.4 Calorimètre hadronique ou HCAL ». Les photons ne laissent pas de signal dans le trajectographe car ils n'ont pas de charge. Ainsi, un dépot d'énergie dans le calorimètre électromagnétique associé à une trace dans le trajectographe permet de reconstruire un électron et un dépot d'un photon. De même, le calorimètre hadronique permet la discrimination entre un hadron neutre et un hadron chargé. En effet, un hadron chargé sera associé à un dépot d'énergie dans le calorimètre hadronique ainsi qu'à un rayon de courbure dans le trajectographe alors qu'un hadron neutre sera associé à un dépot d'énergie dans le calorimètre hadronique seulement. À ce stade, il ne reste finalement que les muons qui seront donc reconstruits grâce aux chambres à muons.
Nous avons ainsi une méthode pour reconstuire chaque type de particule détectable par CMS. Mais qu'en est-il pour les particules non observables directement telles que le boson de Higgs ?
4. Étude de particules non observables directement : l'exemple du boson de Higgs
Afin de montrer comment la reconstruction de particules observables permet l'étude de celles non observées directement, nous allons nous appuyer sur l'article : A measurement of the Higgs boson mass in the diphoton decay channel de la collaboration CMS [4].
4.1 Principe et objectif de l'étude
L'objectif est d'étudier le boson de Higgs et d'effectuer une nouvelle estimation de sa masse \(m_H\), en améliorant la précision de celle-ci qui était jusqu'à présent (125,38 ± 0,16) GeV. Pour ce faire, les nouvelles estimations de \(m_H\) vont concerner le mode de désintégration H → γγ, soit un boson de Higgs se désintégrant en 2 photons. Ces nouvelles mesures seront combinées aux précédentes qui se sont basées sur d'autres modes, afin de réduire l'incertitude sur \(m_H\). L'ensemble des analyses se fait sur les données recueillies en 2016 pour les collisions de protons à 13 TeV. Le principe de l'estimation de la masse du boson de Higgs sera présenté dans cette partie en s'appuyant sur la démarche de l'article [4].
4.2 Détermination des évènements candidats et modélisation
Au regard du mode de désintégration étudié, les particules détectables considérées sont une paire de photons issus de la désintégration d'un même boson de Higgs et qui sont donc corrélés. Autrement dit, l'état du photon 1 dépend de celui du photon 2 et réciproquement. Ces photons sont reconstruits comme présenté dans la section intitulée « 3. Reconstruction de particules observables », et cette reconstruction nous permettra de déduire \(m_H\) via la masse invariante du diphoton \(m_{\gamma \gamma}\) obtenue, car \(m_H\ = m_{\gamma \gamma}\) par conservation de la masse au cours de la désintégration. Toutefois, comment s'assurer que deux photons reconstruits sont issus de la désintégration d'un même boson de Higgs ? En effet, les photons peuvent provenir d'autres processus physiques ou de bosons différents. Les mesures issues de ces processus qui ne sont pas d'intérêt s'apparentent donc à un bruit de fond. De plus, s'ils proviennent bien de la désintégration d'un boson de Higgs, il faut être certain que ce soit du même. Il est donc nécessaire de sélectionner les bons candidats parmi les couples de photons détectés.
La première étape de sélection est un critère quantitatif. Il est nécessaire que l'impulsion transverse de chacun des deux photons (\(p_T^{\gamma1}\), \(p_T^{\gamma2}\)) respecte [4] :
\( p_T^{\gamma1} > \frac{m_{\gamma \gamma}}{3} \) et \( p_T^{\gamma2} > \frac{m_{\gamma \gamma}}{4} \)
où \(p_T^{\gamma1}\) représente l'impulsion transverse du premier photon détecté et \(p_T^{\gamma2}\) celle du second.
De plus, \(m_{\gamma \gamma}\) doit être comprise entre 100 et 180 GeV. Ces contraintes s'apparentent à celles à imposer pour qu'une paire de photons soit détectable. Ensuite, lors de leur arrivée dans le calorimètre électromagnétique, l'énergie libérée ne sera pas contenue dans un seul cristal. Au contraire, elle se propagera en formant des clusters, représentés en figure 9 par les traces foncées dans le calorimètre. Ces clusters seront combinés pour former des superclusters devant satisfaire à des conditions particulières de sensibilité (pseudo-rapidité). En dehors de ces régions, les gerbes électromagnétiques créées par les photons dans l'ECAL sont mal contenues. Les mesures sur l'impulsion qui en découlent sont donc imprécises. Ces premiers critères permettent d'exclure un certain nombre d'évènements non intéressants. Par conséquent, il reste un « bruit ». N'étant pas capable de le supprimer, l'objectif est de le modéliser. Pour ce faire, les évènements donnant un couple de photons pour état final mais ne provenant pas du mode de désintégration H → γγ sont répertoriés. On prévoit leur apparition pour avoir une modélisation de leur distribution de probabilité. Ce sera donc le « bruit » de la mesure. Une fois cela fait, une modélisation du signal attendu lorsque le couple de photons détectés provient bien d'un même boson de Higgs est effectuée.
Finalement, en combinant ces deux modélisations, nous obtenons une dernière modélisation des résultats attendus sous forme de distribution de probabilité d'évènements selon \(m_{\gamma \gamma}\).
4.3 Résultats
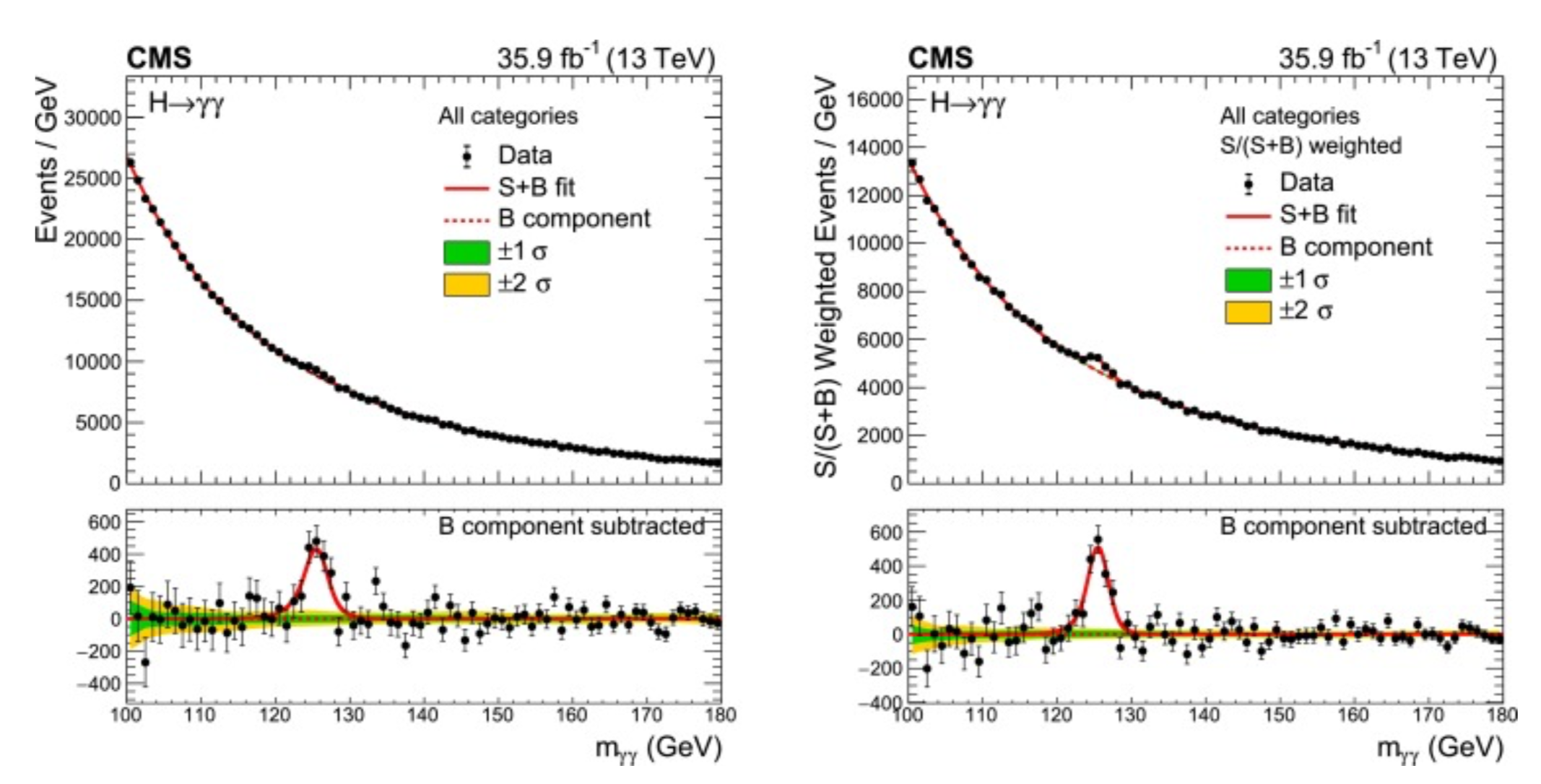
Nous allons donc analyser le nombre d'évènements obtenus selon les valeurs de \(m_{\gamma \gamma}\) et chercher celles qui correspondent à la désintégration d'un boson de Higgs en deux photons parmi toutes celles enregistrées. Nous cherchons donc une perturbation d'une distribution de probabilité de \(m_{\gamma \gamma}\). Notons que cette distribution de probabilité n'est pas uniforme. Pour deux paires de photon d'énergies différentes, il sera plus fréquent d'obtenir celle dont l'énergie est la plus faible comparativement à l'autre paire. Ainsi, le nombre d'évènements détectés est plus important autour de 100 GeV qu'autour de 180 GeV. Les résultats de l'expérience sont récapitulés en figure 10.
Source : CMS Collaboration Physics Letters B 2020, 805 [4]. |
Nous remarquons tout d'abord que la distribution de probabilité n'est pas uniforme comme expliqué précédemment. Mais nous remarquons également un pic sur cette distribution autour de \(m_{\gamma \gamma}\) ≈ 125 GeV. Il traduit la présence du boson de Higgs qui a perturbé anormalement cette distribution. Nous observons donc sa présence indirectement. C'est ce cheminement que les scientifiques du LHC ont suivi pour aboutir à sa découverte. Dans le cadre de notre étude, l'objectif est d'affiner la mesure de la masse du boson de Higgs. La modélisation combinée du signal et du bruit est représentée en trait plein rouge sur les figures 10. Cette modélisation est ajustée sur les données observées expérimentalement afin d'en tirer la masse du boson de Higgs. Grâce à plusieurs techniques d'optimisation que nous ne détaillerons pas ici, l'expérience a donc estimé mH = 125.78 ± 0,18 (stat) ± 0,18 (syst) GeV par une approche asymptotique (où « stat » désigne l'erreur liée au traitement statistique des données et « syst » l'erreur systématique).
Finalement, après avoir combiné ce résultat avec les précédentes études, leur estimation de la masse du boson de Higgs est :
mH = (125.78 ± 0,14) GeV
C'est à ce jour la mesure la plus précise de mH.
5. Conclusion
Comme montré dans cet article qui n'a pourtant abordé que de façon générale la thématique, la technologie du détecteur CMS est très complexe. Chaque sous-détecteur présente un enjeu scientifique de taille : s'assurer du bon fonctionnement de chaque élément, améliorer la précision des mesures effectuées, ... L'ensemble doit être fonctionnel sur de longues périodes car une étude nécessite une base de données expérimentales de plusieurs milliers d'évènements enregistrés qui seront par la suite triés car tous ne sont pas d'intérêt.
Tous les éléments de la chaîne jouent un rôle dans la reconstruction de particules détectables. C'est la précision des mesures sur ces particules-ci qui permettra une mesure précise des caractéristiques des particules non observables directement comme l'a montré l'estimation de la masse du boson de Higgs. Assurer le fonctionnement en continu du détecteur n'empêche toutefois pas les scientifiques du CERN d'améliorer constamment le LHC. Ce sont ces améliorations qui permettent d'ouvrir la voie à de nouvelles perspectives dans la recherche physique. Le colloque « Storage Rings and Gravitational Waves » a récemment discuté de l'importance des accélérateurs de particule dans l'étude des ondes gravitationnnelles. Le LHC est naturellement au premier plan dans ces discussions qui, pour la première fois, dépassent le simple cadre de la recherche en physique des particules.
Enfin, d'autres projets sont à l'étude au CERN, comme celui d'un accélérateur linéraire : le Collisionneur linéaire compact (CLIC).
Remerciements
Je tiens à remercier chaleureusement Lucas Torterotot pour avoir pris le temps durant sa dernière année de thèse de m'aiguiller dans mes recherches. Son aide m'a été plus que précieuse pour interpréter et parfois même décrypter les différents articles de recherche utilisés dans la conception de cet article. Ce travail n'aurait pas été possible sans son investissement continu.
Références
- [1] Les titans du CERN, https://lejournal.cnrs.fr/diaporamas/les-titans-du-cern, CNRS Le Journal, consulté en mai 2022.
- [2] le site du CERN, Resources, consulté en mai 2022.
- [3] Hugues Lattaud,Photon et jets avec l'expérience CMS du LHC : de la calibration à la mesure, Thèse de doctorat.
- [4] CMS Collaboration, Physics Letter B 2020, 805.
On peut retrouver cet article dans sa version première, dans le Journal de Physique et de Chimie des étudiants de l'ENS de Lyon « L'expérience CMS au LHC »
[1] Les hadrons sont composés de particules régies par l'interaction forte dont les gluons sont les vecteurs. Parmi les hadrons on trouve les protons, les neutrons, les mésons…
Pour citer cet article :
L'expérience CMS au LHC, Théo Moret, septembre 2022. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/CMS-Moret.xml