Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Vitesse superluminique en astronomie
26/04/2012
Résumé
Cet article montre comment la vitesse transverse apparente de déplacement d’un objet lointain peut apparaître supérieure à la vitesse de la lumière. Il s’agit d’un effet de projection géométrique de la vitesse réelle qui ne dépasse jamais celle de la lumière. Comme exemple, on détaille l’observation d’un jet relativiste issu de la galaxie active géante M87.
Un article du dossier « La vitesse de la lumière ».
Table des matières
Première version de l'article : 12 - 09 - 2003
Les observations astronomiques permettent de déterminer la vitesse de déplacement des astres. D’une part la vitesse « radiale », c’est-à-dire projetée sur la ligne de visée, est déduite du décalage Doppler-Fizeau des raies spectrales. D’autre part on évalue la vitesse relative du déplacement transverse en mesurant l’écart angulaire entre deux astres à deux époques différentes. Dans certains cas la vitesse transverse apparaît supérieure à la vitesse de la lumière. Il s’agit d’une illusion due à l’effet de projection géométrique d’une vitesse réelle qui est parfois très proche de celle de la lumière, mais qui ne la dépasse pas. Comme exemple et application numérique, le jet « superluminique » de la galaxie M37 est décrit en détail à partir des observations du téléscope spatial Hubble.
Les astronomes semblent voir des objets (jets de plasma, etc...) se déplacer plus vite que la lumière !
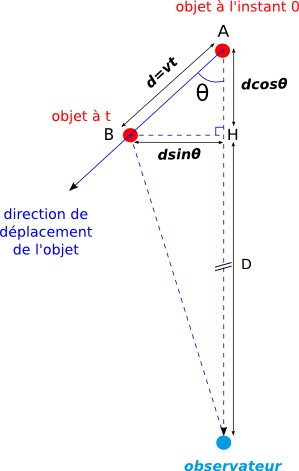
La figure 1 représente la géomètrie particulière d’une observation astronomique qui conduit à déterminer une vitesse superluminique. L’observateur (point bleu) repère un objet lumineux (point rouge) qui se déplaçe rapidement.
A l’instant 0, l'objet émet de la lumière en A. Celle-ci n'atteint pas instantanément l'observateur mais doit parcourir la très gande distance D pour arriver jusqu'à lui.
L'objet se déplace à la vitesse v suivant une direction qui fait une angle θ avec la direction d'observation. Donc à l'instant t, l'objet s'est déplacé d'une distance .
Entre les deux positions A et B de l'objet, il s'est écoulé la durée t. L'observateur recoit la lumière issue de A et B à des instant tA et tB; l'intervalle tB-tA étant différent de t.
La distance D étant très grande devant la projection BH de la distance d parcourue par l’objet, on a :
- le signal émis par l'objet passant en A à l'instant 0 est reçu à l'instant tA.
- le signal émis par l’objet passant en B à l’instant est reçu à l’instant tB .
car
Durant l'intervalle de temps , l'observateur voit que l'objet s'est déplacé de la distance .
Il en déduit la vitesse transverse apparente :
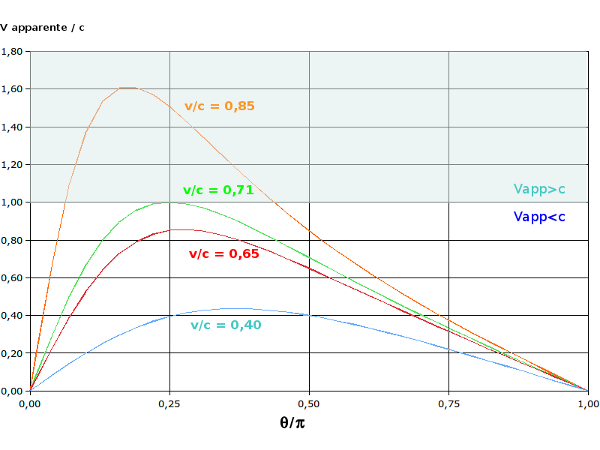
La figure 2 représente des variations de la vitesse apparente en fonction de θ pour différentes valeurs du rapport . On voit que les courbes passent par un maximum (il a lieu pour )
La vitesse apparente maximum est supérieure à la vitesse de la lumière si .
La zone des vitesses apparentes superluminiques est indiquée en bleu sur le graphe de la figure 2.
On voit ainsi qu'il est possible d'observer des mouvements apparents plus rapides que la lumière, alors même que l'objet est très rapide, certes, mais plus lent que c. Comme il ne s'agit que d'une illusion, il n'y a pas de contradiction avec la théorie de la relativité. On peut, moyennant d'autres observations (décalage spectral, etc...) retrouver le déplacement réel d'un objet dans le ciel et vérifier ainsi que sa vitesse véritable était bien inférieure à celle de la lumière dans le vide.
Exemple d'observation de jets cosmologiques avec des vitesses apparentes superluminiques
La figure 3 montre des observations de la galaxie M87 obtenues par le télescope spatial Hubble. L’image du haut donne l’aspect général du jet lumineux issu de cette galaxie elliptique géante située à 52,5 millions d’années-lumière de la Terre. La planche du bas donne des images agrandies de la zone proche du noyau (notée par un carré) et souligne l’évolution de quatre nodules durant cinq années d’observation.
Figure 3. Mouvement superluminique du jet de M87
Le noyau actif de la galaxie M87 est constitué d’un trou noir supermassif qui absorbe l’environnement galactique, tandis qu’un immense jet relativiste directif éjecte de la matière à très grande vitesse. On observe ici le noyau actif (point lumineux à gauche) et l'énorme jet lumineux sur une extension de 2600 années-lumière environ (correspondant à un angle α de 10 secondes).
Dans le jet apparaissent des structures lumineuses, ou nodules, créées par des ondes de choc aux points où le jet heurte des régions plus denses.
On voit sur la planche détaillée que les nodules s’écartent du noyau à raison d’environ 0,024 seconde d’angle par an, ce qui correspond aux vitesses apparentes indiquées, de l’ordre de 6 fois la vitesse de la lumière.
L'année-lumière (notée a.l.) est la distance parcourue par la lumière dans le vide, en une année.
Application numérique :
Avec les données numériques indiquées sur la figure 4, on vérifie l'évaluation de la vitesse apparente tranverse :
Notons que l'observation des détails du jet est réalisée avec une résolution angulaire meilleure que 0,024”. Ceci n'est possible que parce que le télescope spatial Hubble est situé hors de l' atmosphère. Si l'observation était faite du sol, l'atmosphère limiterait la résolution angulaire à environ 1” (selon la turbulence atmosphèrique).
Pour déterminer les vitesses réelles des nodules observés, il faut un modèle plus réaliste tenant compte de l’angle d’inclinaison θ du jet par rapport à la ligne de visée. Un des modèles proposé par l’article dont sont issus ces données (Biretta et al., The Astrophysical Journal, 1999, 520, 621) donne une valeur de θ comprise entre 10° et 19°, ce qui correspond à un jet relativiste de vitesse supérieure à 0,986 c.
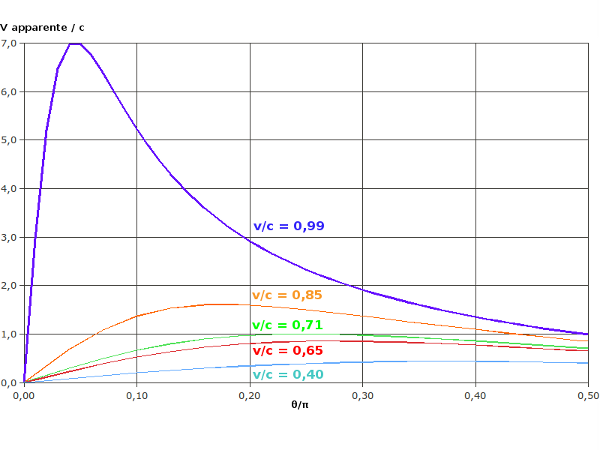
La courbe bleue montre la variation théorique pour en fonction de l’angle θ (les autres courbes correspondent à celles de la figure 2 décrite dans la première partie de l'article ).
Pour on voit que la vitesse apparente observée de 6c est bien prévue dans la zone , soit .
Conclusion
Il est actuellement admis par tous les physiciens qu’un objet matériel, ou une information, ne peut pas se déplacer plus vite que la lumière dans le vide. Nous venons de voir que des vitesses superluminiques observées en astronomie s’expliquent par une simple illusion d’optique, due au décalage temporel induit par le temps que met la lumière pour arriver jusqu'à nous.
Dans l'article précédent « Plus vite que la lumière : effet Cherenkov », on montre qu’une particule peut aller plus vite que la lumière si la propagation se fait dans un milieu d’indice supérieur à un, mais la vitesse de la particule reste inférieure à la vitesse de la lumière dans le vide.
Référence
- Les images observées se trouvent sur le site du téléscope spatial Hubble
- L’article original est de Biretta et al., The Astrophysical Journal, 1999, 520, 621
Téléchargement
Une version format pdf est téléchargeable "Vitesse superluminique en astronomie format pdf" pour les utilisateurs présentant des problèmes d'affichage des formules mathématiques.
Article précédent : « Plus vite que la lumière : effet Cherenkov ».
Dossier : « La vitesse de la lumière ».
Pour citer cet article :
Vitesse superluminique en astronomie, Gabrielle Bonnet, Mathilde Glenat, avril 2012. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/vitesse-superluminique.xml