Activer le mode zen
Ressource au format PDF
Mots-clés
- tsunami
- onde
- océan
- propagation
Classification
Fabriquons des tsunamis !
23/03/2016
Cet article est le fruit du travail des membres des Laboratoires Juniors « Initiation à la dynamique des fluides planétaires » (responsable : Marine Lasbleis) et « Médiation autour de la géophysique » (responsable : Christophe Brouzet).
Résumé
Comprendre la génération, la propagation et le déferlement des tsunamis pour s'en prémunir.
Table des matières
Les tsunamis sont des phénomènes naturels très médiatisés à cause des dégâts humains et matériels extrêmement importants que ceux-ci peuvent causer. Afin de mieux protéger les populations menacées par des tsunamis, il est important de comprendre les mécanismes physiques mis en jeu lors de leur génération, leur propagation et leur déferlement. Cet article permet d’expliquer simplement les caractéristiques des tsunamis tout en décrivant une expérience reproductible devant une classe du primaire ou du secondaire. Dans chaque partie, nous détaillerons à la fois les éléments théoriques et expérimentaux de chaque étape de la vie d’un tsunami.
1. Un tsunami, une onde solitaire
Un tsunami est une onde océanique, marine ou lacustre pouvant se propager sur de très grandes distances à la surface de l’eau. C’est généralement une onde solitaire, c’est-à-dire qu’il y a seulement un endroit où l’eau est surélevée. Cette onde diffère ainsi des vagues que l’on a l’habitude de voir en mer et qui, elles, ne sont pas solitaires et sont essentiellement engendrées par le vent.
Pour étudier de façon expérimentale les tsunamis, nous proposons de prendre une cuve pour modéliser un océan à une dimension, ayant une largeur petite par rapport à sa longueur. La propagation de l’onde expérimentale sera d’autant plus facile à visualiser que la cuve-océan sera longue. La cuve utilisée pour nos expériences est une cuve en plexiglas de 2 mètres de long, 40 centimètres de haut et 17 centimètres de large. Une photo de la cuve est montrée sur la figure 1.
2. Génération des tsunamis
Bien que les tsunamis soient des ondes se propageant à la surface de l’eau, leur origine vient souvent du fond de l’océan. Ils sont causés par un déplacement brutal d’une grande quantité d’eau. Ce déplacement d’eau est essentiellement créé par un séisme ou un glissement de terrain sous-marin. Néanmoins, il peut également être provoqué par l'éboulement d’une falaise dans l’eau. Dans les deux cas, un tsunami est créé en surface et se propage.
Dans le cas de notre expérience, nous ne reproduisons pas le séisme mais directement le déplacement d’eau à l’origine du tsunami. À une extrémité de la cuve, il suffit d’enfoncer un piston dont la largeur est proche de celle de la cuve pour créer une onde qui va ensuite se propager vers l’autre extrémité de la cuve.
Source - © 2016 Laboratoire junior « Initiation à la dynamique des fluides planétaires » Figure 2. Propagation et déferlement de l'onde |
3. Propagation des tsunamis
3.1 Forme d'un tsunami
Un tsunami se propage dans un fluide et obéit donc à l’équation de la dynamique régissant le mouvement des fluides, l’équation de Navier et Stokes. En partant de cette équation, Korteweg et de Vries démontrèrent en 1895 que l’évolution de l’enveloppe du tsunami obéit à une équation différentielle adimensionnée, appelée équation de KdV (par la suite), reliant les différentes dérivées de l’élévation de la hauteur d’eau adimensionée, Φ (x,t).
(1) |
où t représente le temps adimensionné et x la distance adimensionnée dans la direction de propagation.
D’après cette équation, on constate que la variation temporelle de l’enveloppe est reliée à :
- un phénomène de propagation dispersive, par le terme :
- et un phénomène non-linéaire, par le terme :
Ces deux phénomènes vont avoir des effets antagonistes. Le terme dispersif va avoir tendance à étaler le tsunami. À l’inverse, en un x donné, grâce au terme non-linéaire, Φ (x,t) va augmenter d’autant plus que Φ (x,t) est grand. Le terme non-linéaire va donc favoriser le resserrement de la vague. Ainsi un tsunami peut voyager en gardant sa forme sur des milliers de kilomètres. Si on s’intéresse à un tel tsunami qui se propage à la célérité adimensionnée cadim, on peut alors écrire que : et simplifier l'équation (1) en :
(2) |
soit en intégrant, on obtient :
(3) |
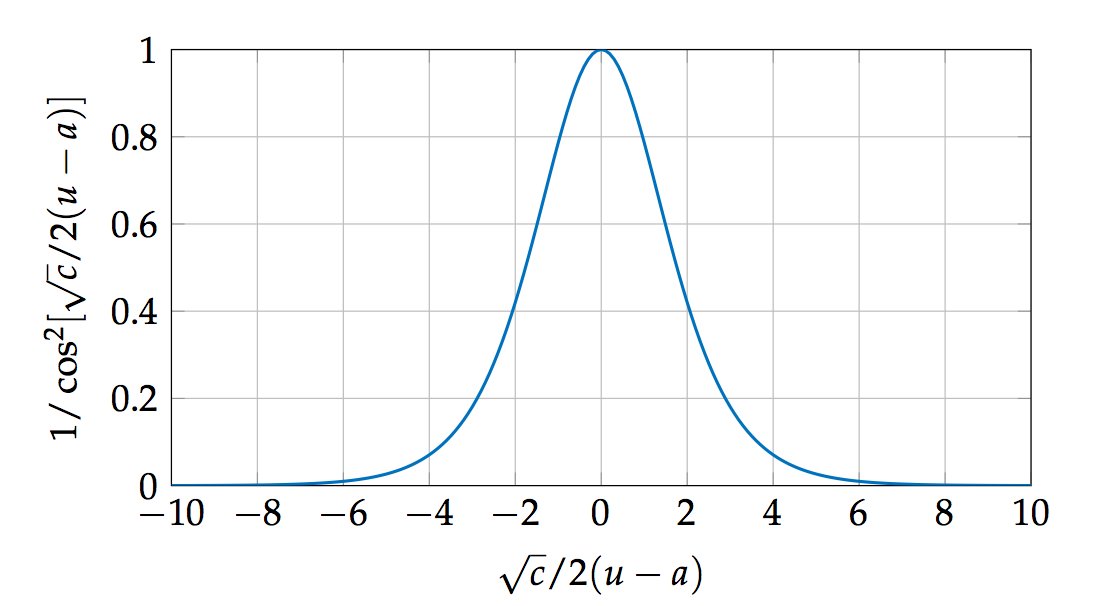
où a est une constante. Cette équation différentielle est donc valable dans le référentiel associé au tsunami, c’est-à-dire dans celui se déplaçant à la même vitesse que le tsunami et dans lequel le tsunami parait donc immobile. La solution de cette équation est donnée par :
(4) |
La solution de cette équation est représentée sur la figure 3.
Qualitativement, on retrouve cette forme sur la figure 4, extraite de la vidéo figure 2.
Source - © 2016 Laboratoire junior « Initiation à la dynamique des fluides planétaires »
La vague est ici sur le point d’atteindre la pente, symbolisant la côte. Image extraite de la vidéo figure 2.
C'est cette non-linéarité qui explique pourquoi un tsunami créé au Japon par un séisme peut atteindre les côtes de l’Amérique du Sud en traversant tout l’Océan Pacifique. C’est en cela que réside un de ses principaux dangers. Les zones touchées par un tsunami peuvent être très éloignées du phénomène qui lui a donné naissance.
3.2 Vitesse d'un tsunami
Un tsunami a une largeur de l’ordre de 200 km. À cette échelle, l’océan apparaît comme très peu profond, celui-ci ne fait que quelques kilomètres de profondeur. Un tsunami est donc équivalent à une vague sur une très fine couche d’eau. Dans cette configuration, la vitesse c des vagues est donnée par :
(5) |
où g est l’accélération de la pesanteur et h la profondeur de l’océan. Pour un océan d’une profondeur de 4 km on obtient une célérité typique de c ≈ 200 m/s soit 720 km/h. Cette formule n’est en réalité valable que dans le domaine des ondes linéaires, ce qui n’est pas le cas d’un tsunami, car sa dynamique est non-linéaire. Cependant, la correction apportée par le terme non-linéaire est faible et la vitesse trouvée est très proche de la réalité. Du fait de sa vitesse, un tsunami créé au large du Japon peut arriver en Amérique du Sud en moins d'une journée (environ 21 heures). Ainsi, non seulement un tsunami se propage sur de grandes distances mais il se propage également très vite.
Expérimentalement, comme la profondeur d’eau dans la cuve est relativement faible devant la longueur d’onde de la vague générée, on peut estimer sa vitesse en utilisant l’équation (5). Avec une profondeur d’eau de 10 cm environ, on trouve que c ≈ 1 m/s, ce qui est cohérent avec ce que l’on peut observer. Cela laisse à l’observateur le temps d’apercevoir le profil de la vague lors de sa propagation.
3.3 Hauteur d'eau
Nous avons pour le moment caractérisé les tsunamis comme étant des vagues solitaires, pouvant se propager sans déformation à des vitesses très élevées. Qu’en est-il de l’élévation d’eau provoquée par le passage d’un tsunami ?
Pour un tsunami se propageant sans déformation, la résolution complète de l’équation de KdV montre que la hauteur d’élévation de l’eau est inversement proportionnelle à la profondeur d’eau alors que la distance sur laquelle l’eau est surélevée est proportionnelle à la racine carrée de la profondeur d’eau. En plein océan, la hauteur de la vague ne dépasse pas un mètre et le tsunami peut s’étaler sur plusieurs centaines de kilomètres. Cela signifie qu’un tsunami passe complètement inaperçu en haute mer pour les bateaux, car il est masqué par la houle.
Cependant, lorsqu’il arrive près des côtes la profondeur d’eau diminue. Par conséquent, le tsunami voit sa largeur se rétrécir et sa hauteur d’eau fortement augmenter. C’est d’ailleurs ce phénomène qui a donné le nom tsunami. En effet, nami signifie « vague » en japonais tandis que tsu désigne une « baie », une anse sur la côte, là où étaient installés les ports de pêche. Tsunami signifie donc littéralement « vague portuaire ». Les pêcheurs, partis au large pendant le passage d’un tsunami, ne ressentaient ni ne voyaient rien de particulier. En retournant sur la côte, ils constataient les dégâts qu’avaient faits ces gigantesques vagues. On pensait à l’époque que ces vagues se formaient près des côtes d’où leur nom.
4. Arrivée sur les côtes et déferlement des tsunamis
Lorsque le tsunami arrive près des côtes, la profondeur d’eau diminue. Il subit alors plusieurs effets : le tsunami ralentit mais il grandit fortement et se resserre car l’importance de la non-linéarité augmente et celle de la dispersion diminue. La vague se déforme et son profil se raidit puis casse : il y a déferlement. L’eau avance dans les terres et c’est cela qui peut causer des dégâts importants.
Quelques minutes avant l’arrivée d’un tsunami on peut constater un retrait de l’eau au niveau du rivage de plusieurs centaines de mètres. Lorsque l’on constate ce retrait il est préférable de se mettre à l’abri rapidement. En effet, on peut calculer le délai avant lequel le tsunami arrive. Pour cela il suffit de diviser sa largeur typique par sa vitesse, on obtient alors un temps d’environ 10 minutes.
Il peut néanmoins y avoir plusieurs types de déferlement selon le profil sous-marin de la côte. Si le fond remonte très rapidement ou très lentement, la vague va déferler mais ne va pas former de rouleaux, tant appréciés des surfeurs sur des vagues moins grandes qu’un tsunami. En revanche, lorsque le fond marin remonte de façon adéquate, un rouleau se forme lors du déferlement.
Dans notre expérience, une pente modélise la côte. On peut très facilement modifier l’angle que fait cette pente avec le fond de la cuve pour en étudier les effets sur le déferlement du tsunami. On voit bien que pour de faibles ou de forts angles, la vague déferle mais ne forme pas de rouleaux. Pour un angle intermédiaire, compris entre 5 et 10 degrés, la vague déferle en formant un rouleau. C’est ce que l’on voit sur la figure 5 et dans la vidéo de la figure 6.
Source - © 2016 Laboratoire junior « Initiation à la dynamique des fluides planétaires »
On y voit le rouleau de la vague en train de se former. Image extraite de la vidéo figure 2.
La vidéo ci-dessous reprend tous les paramètres présentés et met en évidence les différents types de déferlement selon l'inclinaison du profil sous-marin de la côte.
Source - © 2016 Laboratoire junior « Initiation à la dynamique des fluides planétaires » Réalisation : ChezMoiProd avec le Laboratoire junior « Initiation à la dynamique des fluides planétaires ». Figure 6. Expérience du déferlement d'un tsunami |
5. Prévention contre les tsunamis
Afin de limiter les dégâts engendrés par les tsunamis, la prévention est réalisée par deux moyens : la détection des tsunamis permettant d’alerter rapidement la population en cas de danger et la prévention à long terme dans les zones à risque.
5.1 Détection des tsunamis et systèmes d'alerte
Lorsqu’un séisme sous-marin survient, celui-ci est détecté par les réseaux de sismomètres, déployés sur terre et dans les fonds marins par les systèmes d’alerte internationaux tels que le PTWC (centre d’alerte des tsunamis dans le Pacifique, basé à Hawaï) et les systèmes d’alerte régionaux. En parallèle, les capteurs de pression sous-marins du réseau marégraphique mesurent en continu l’évolution du niveau de la mer pour différentes positions dans l’océan. Toutes ces informations sont ensuite transmises aux centres d’alerte, par l’intermédiaire de bouées à la surface de l’eau et de satellites en orbite.
L’analyse des caractéristiques du séisme permet de prédire si le risque de formation d’un tsunami est élevé, ou non. Si c’est le cas, des simulations numériques permettent alors de calculer le temps d’arrivée de la première vague sur les côtes, et un message d’alerte est envoyé aux organismes chargés de faire évacuer la population dans les zones à risque.
Dans les zones équipées, le message d’alerte est généralement transmis à la population dans les 10 ou 15 minutes qui suivent le séisme, par le biais de sirènes municipales, de messages aux haut-parleurs sur les plages, et d’annonces à la radio et à la télévision. Cela permet d’effectuer l’évacuation avant l’arrivée du tsunami dans la majorité des cas, à condition que les consignes d’évacuation soient parfaitement maitrisées et appliquées par la population. Cependant, pour les zones situées à proximité de l’épicentre du séisme, ce délai est insuffisant et les conséquences sont alors désastreuses.
5.2 Prévention à long terme
La création de bases de données recensant les caractéristiques de plusieurs centaines de tsunamis a permis d’améliorer considérablement la compréhension et la modélisation de ce phénomène. Ces connaissances permettent alors une meilleure prédiction de l’apparition d’un tsunami, et une meilleure évaluation de son amplitude et de sa vitesse, à partir des données sismiques recueillies. La cartographie des zones à risque joue également un rôle essentiel. Elle permet de mettre en place des mesures préventives (dispositifs anti-tsunamis, éducation de la population, installation de système d’alerte) pour être plus efficace en cas de danger.
À ce jour, plusieurs dispositifs anti-tsunamis ont été développés afin de réduire les dégâts engendrés. Le plus utilisé consiste en la réalisation de gigantesques murs de béton, comme celui de Taro, au Japon, haut de 11 mètres. Cependant, ces murs ne sont pas efficaces face à des tsunamis de grande ampleur, et peuvent même aggraver les dégâts car ils empêchent l’eau de s’évacuer si un tsunami particulièrement puissant passe cette barrière. Les autres dispositifs tels que des digues brise-lames ou des forêts de mangrove ont également une efficacité limitée sur les vagues de grandes amplitudes. La meilleure façon de se protéger des tsunamis reste de ne pas construire d’habitations sur les premiers kilomètres à proximité du rivage, ou si possible de les construire sur les hauteurs.
6. L'avis du chercheur
Thomas Peacock, chercheur au MIT (Massachusetts Institute of Technology) nous présente ses recherches sur les tsunamis et le protocole expérimental dans la vidéo ci-dessous (durée 6 min 06 s). Ces travaux de recherche concernent les ondes internes dans l'océan et l'atmosphère, les méthodes lagrangiennes pour l'étude des phénomènes de transport pour des écoulements géophysiques et les écoulements de fluides stratifiés.
Source - © 2016 Laboratoire junior « Initiation à la dynamique des fluides planétaires » - ChezMoiProd |
7. La vie du chercheur
Thomas Peacock nous présente son métier de chercheur au MIT (durée 6 min 25 s).
Source - © 2016 Laboratoire junior « Initiation à la dynamique des fluides planétaires » - ChezMoiProd |
Les auteurs remercient l'ensemble des membres du Laboratoire Junior « Initiation à la dynamique des fluides planétaires » : Christophe Perge, Baptiste Bourget, Marine Lasbleis, Charles-Édouard Boukaré et Baptiste Journaux, Mathieu Bouffard, Pierre Labreuche, Arthur Marguerite, Hugo Doré.
Pour citer cet article :
Fabriquons des tsunamis !, Brouzet, Maurer, De Zotti, mars 2016. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/tsunami.xml