Somme de signaux sinusoïdaux de même fréquence mais de phase différente, en langage python

Dans un premier temps, on importe les bibliothèques python nécessaires au traitement des données et à l'affichage des graphiques, figure 1.

Figure 1.  Importation des bibliothèques python utilisées

On choisit arbitrairement de travailler à une fréquence de 200 Hz, figure 2.

On renseigne le temps total ("temps_total") en seconde sur lequel on va construire chacun de nos signaux, ainsi que le pas de temps dt.

On définit le nombre de points "nb_points" du calcul. Il est choisi à l'aide du temps total ("temps_total") avec un échantillonnage au pas de temps "dt" défini précédemment. Le nombre de points est nécessairement un entier, on utilise la fonction int pour ne garder que la partie entière.

On définit alors le vecteur "temps" de la manière suivante :

Définition d'un vecteur (linspace) partant du temps initial (0), au temps final "nb_points", contenant "nb_points" éléments, multiplié par le pas de temps (dt).

Figure 2.  Définition des deux signaux sinusoïdaux Y1, Y2, du déphasage et de leur somme Y3

On souhaite tracer la représentation graphique de ces signaux. Afin de voir quels soucis on peut rencontrer, on propose de travailler avec un signal "test" sinusoïdal Y, défini comme précédemment, figure 3.

La fonction plot appelle la bibliothèque pyplot (plt), on renseigne d'abord l'axe des abscisses (temps), l'axe des ordonnées (Y) et le format du tracé (b-) : un trait bleu relie les points calculés.

Pour afficher le quadrillage, on utilise la fonction plt.grid(True).

Figure 3.  Définition du signal sinusoïdal Y calculé sur une seconde et commande de sa représentation graphique

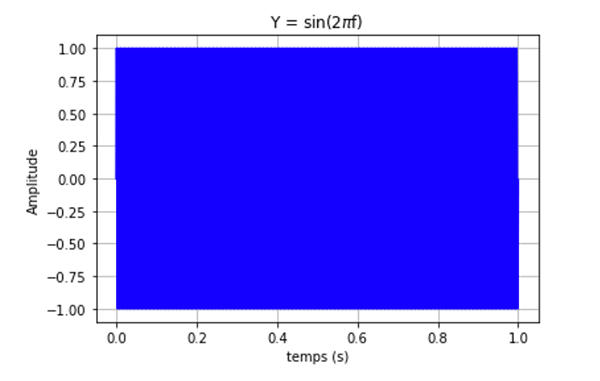
On obtient la figure 4.

Figure 4.  Tracé du signal Y correspondant au code de la figure 3

Le tracé par défaut est réalisé pour tous les points calculés ("nb_points") dans une fenêtre de taille fixée par l'interface, mais il est tout-à-fait illisible.

De la même manière que l'on utilise un oscilloscope en salle de TP, il faut définir une fenêtre de temps adéquate pour pouvoir observer correctement le signal.

Le signal variant 200 fois par seconde, on choisit ici de visualiser 4 périodes en ajoutant la commande plt.xlim(limite inférieure de l'axe des abscisses, limite supérieure). On affiche alors le tracé de 0 à 0,02 seconde, figure 5.

On affiche l'axe du temps en écriture scientifique, pour plus de visibilité, en utilisant la fonction ticklabel_format de la manière suivante :

ticklabel_format (écriture scientifique, axe concerné, prise en compte pour toutes les valeurs du vecteur).

Figure 5.  Définition du signal sinusoïdal Y calculé sur une seconde et commande de sa représentation graphique avec définition des limites sur l'axe des abscisses

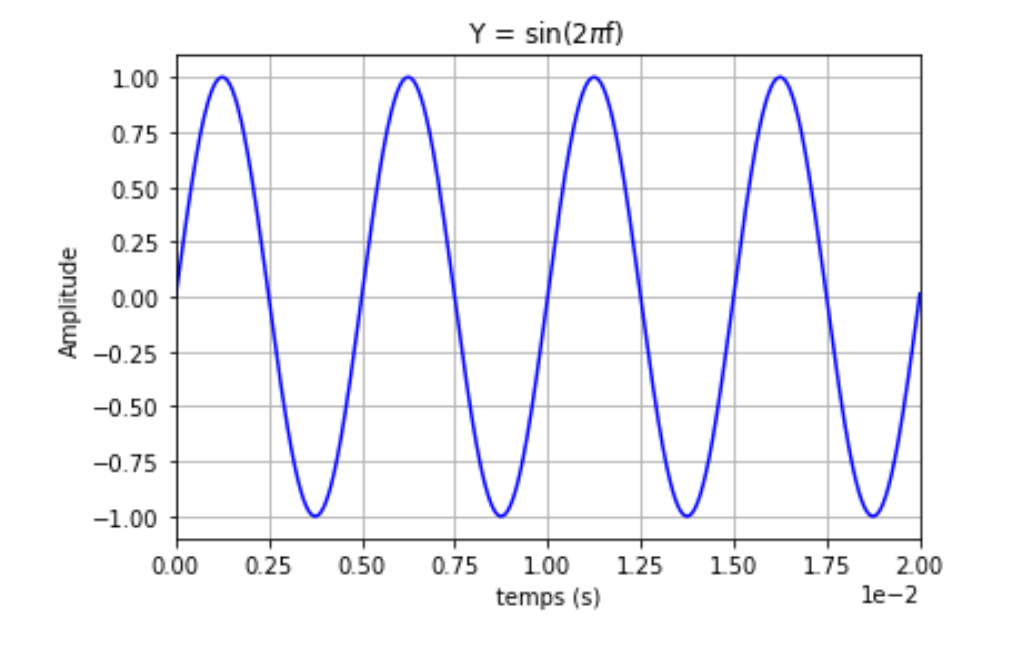
On obtient la figure 6.

Figure 6.  Tracé du signal Y correspondant au code de la figure 5

La définition du pas de temps est très importante au regard du signal que l'on souhaite étudier. C'est elle qui va nous donner la résolution du signal et la précision des calculs.

Pour bien comprendre cela, gardons l'exemple précédent d'un signal sinusoïdal à la fréquence de 200 Hz, en prenant un pas de temps égal à une milliseconde (dt_1 = 10^-3), figure 7.

On ajoute une commande pour l'affichage de la période du signal sinusoïdal et du pas de temps à l'aide de la fonction print.

Figure 7.  Définition de la fonction sinus de fréquence 200 Hz avec un pas de temps de 1 ms

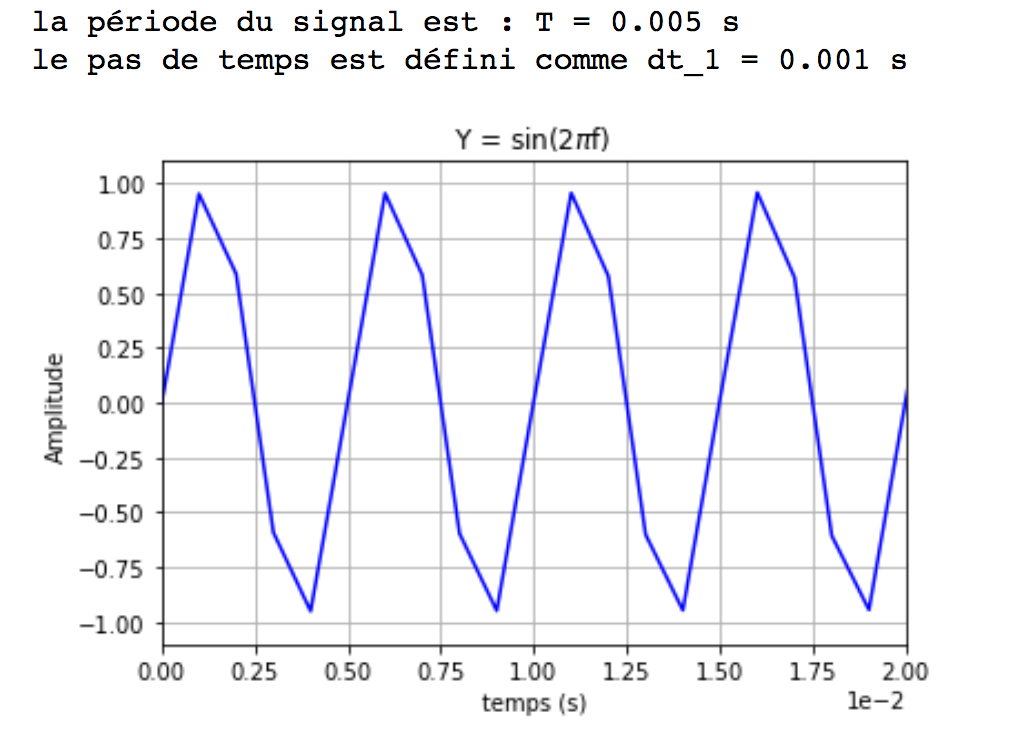
On obtient le tracé et les éléments de la figure 8.

Figure 8.  Tracé du signal Y correspondant au code de la figure 7

La période du signal étant de 5 ms, en utilisant un pas de 1 ms, on constate, en effet, que le signal est défini par 5 points dans une période. Le signal ne ressemble pas à un sinus, il est clairement sous-échantillonné.

Il s'agit alors de trouver un compromis entre la résolution du signal et le nombre de calculs demandés au programme. En effet, plus le signal sera résolu par un grand nombre de points, plus le nombre d'opérations sur le signal sera grand et donc gourmand en temps de calcul.

On prendra ici un facteur 500, de sorte qu'une période soit définie par 500 points.

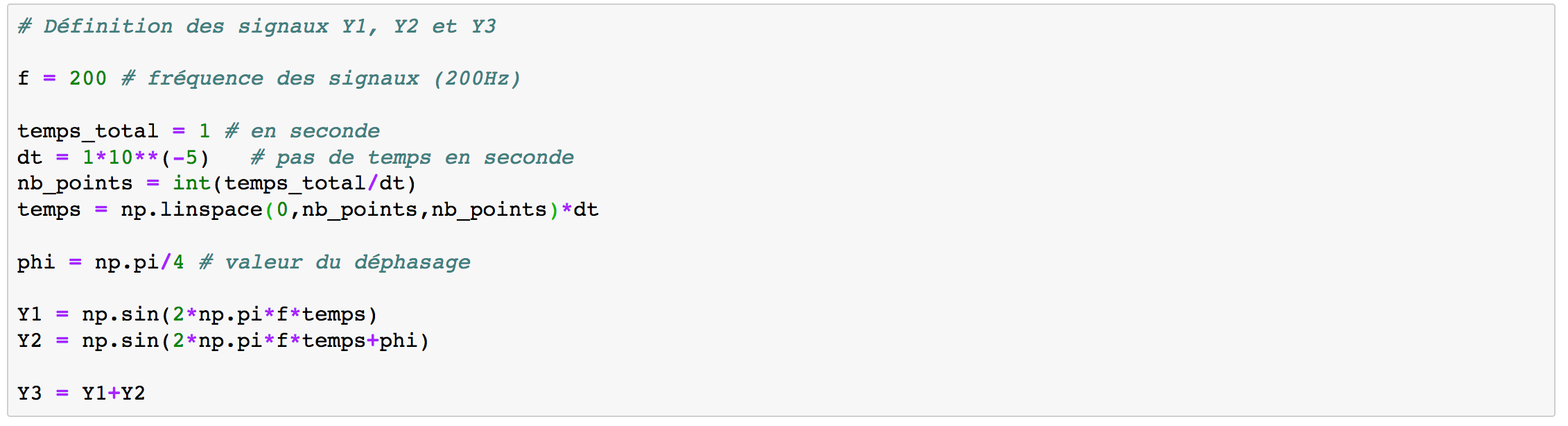
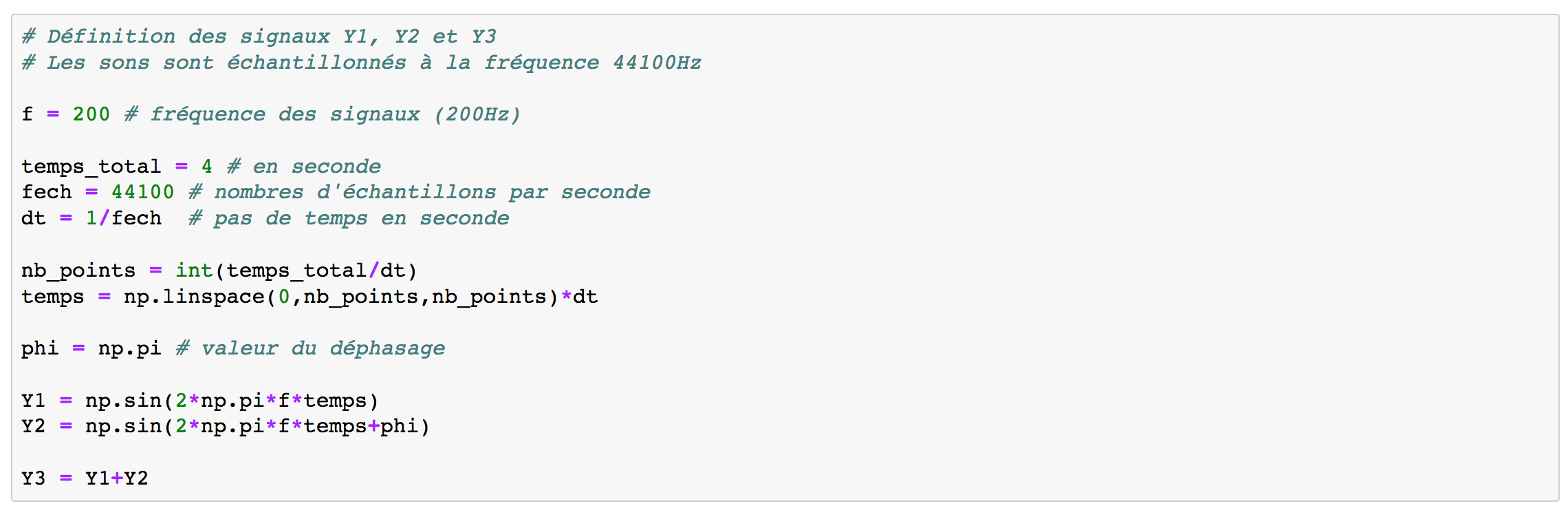
Suite à ces appartés, reprenons le code où l'on a défini les deux signaux sinusoïdaux Y1, Y2, le déphasage et le signal Y3 résultant de leur somme, figure 2.

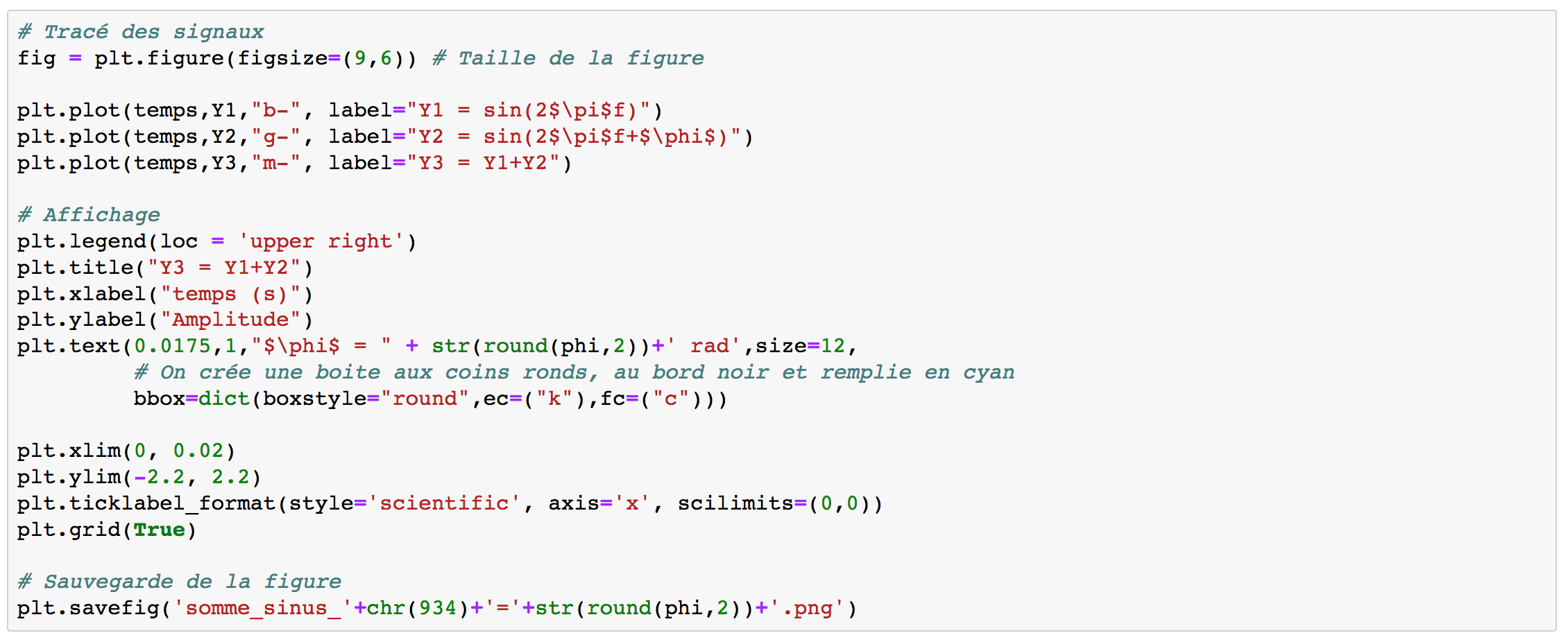
On va représenter les trois signaux sur le même graphique, figure 9. Dans un premier temps, simplement pour plus de visibilité, on agrandit la fenêtre d'affichage à l'aide de la fonction figsize(largeur, hauteur), en pouces.

On choisit de fixer l'emplacement de la légende (en haut à droite) à l'aide de l'attribut loc = 'upper right'.

On souhaite rendre visible la valeur du déphasage sur le graphique. On utilise la fonction plt.text de la manière suivante :

Définition de la boite de texte plt.text (position X de la boite, position Y de la boite, texte contenu dans la boite, taille de la police, puis on définit les attibuts de la boite (bbox) : boite aux coins ronds, au bord noir et remplie en cyan).

Pour comparer plus facilement les courbes pour différentes valeurs de déphsage, on fixe les échelles des ordonnées et des abscisses.

La fonction plt.savefig permet d'enregistrer la figure. Pour obtenir l'affichage du caractère Φ, pour le déphasage, le langage python utilise le caractère Unicode 934, le nom du fichier porte ainsi la valeur du déphasage.

Figure 9.  Instructions pour le tracé des signaux Y1, Y2 , Y3 et l'affichage du déphasage

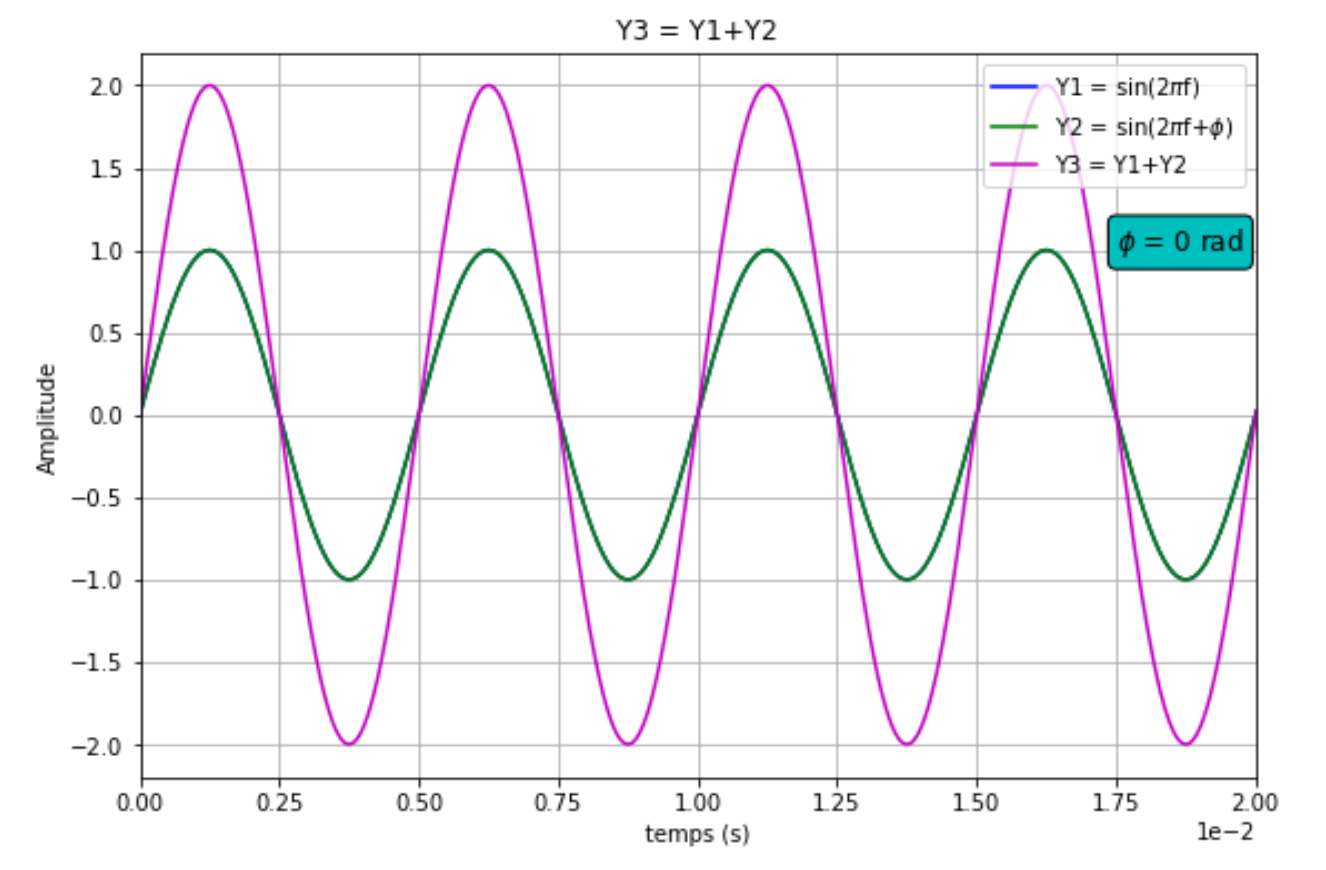
On obtient les tracés correspondants, figure 10. Le déphasage a été initialement fixé à 0 dans le code figure 2.

Figure 10.  Représentation graphique des signaux Y1, Y2 , Y3 correspondant au code de la figure 9

Pour faire varier le déphasage, π est appelé par la bibliothèque numpy. Pour un déphasage de π/2, on notera alors np.pi/2, figure 11.

Figure 11.  Définition des deux signaux Y1, Y2, du déphasage et de leur somme Y3. Le déphasage est maintenant égal à π/2

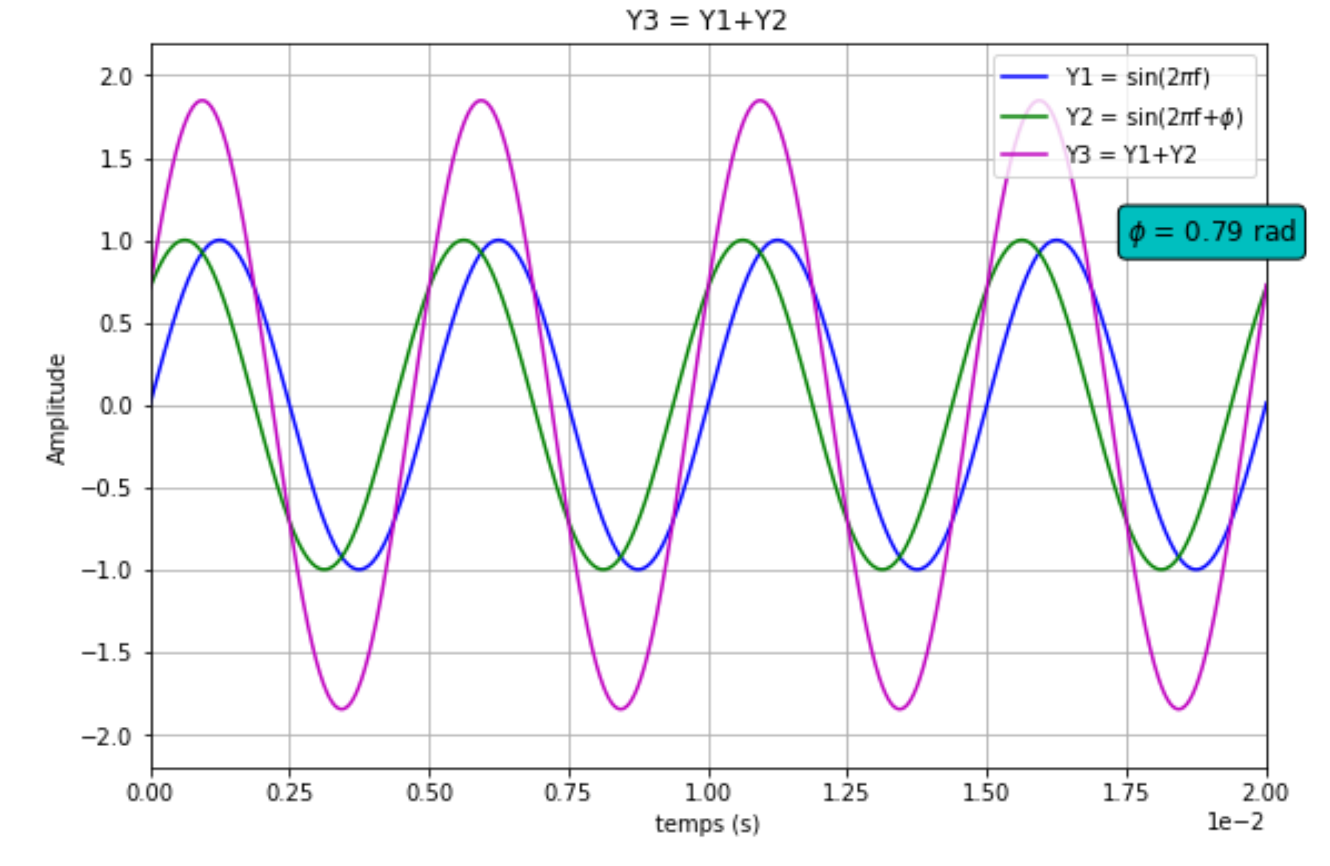
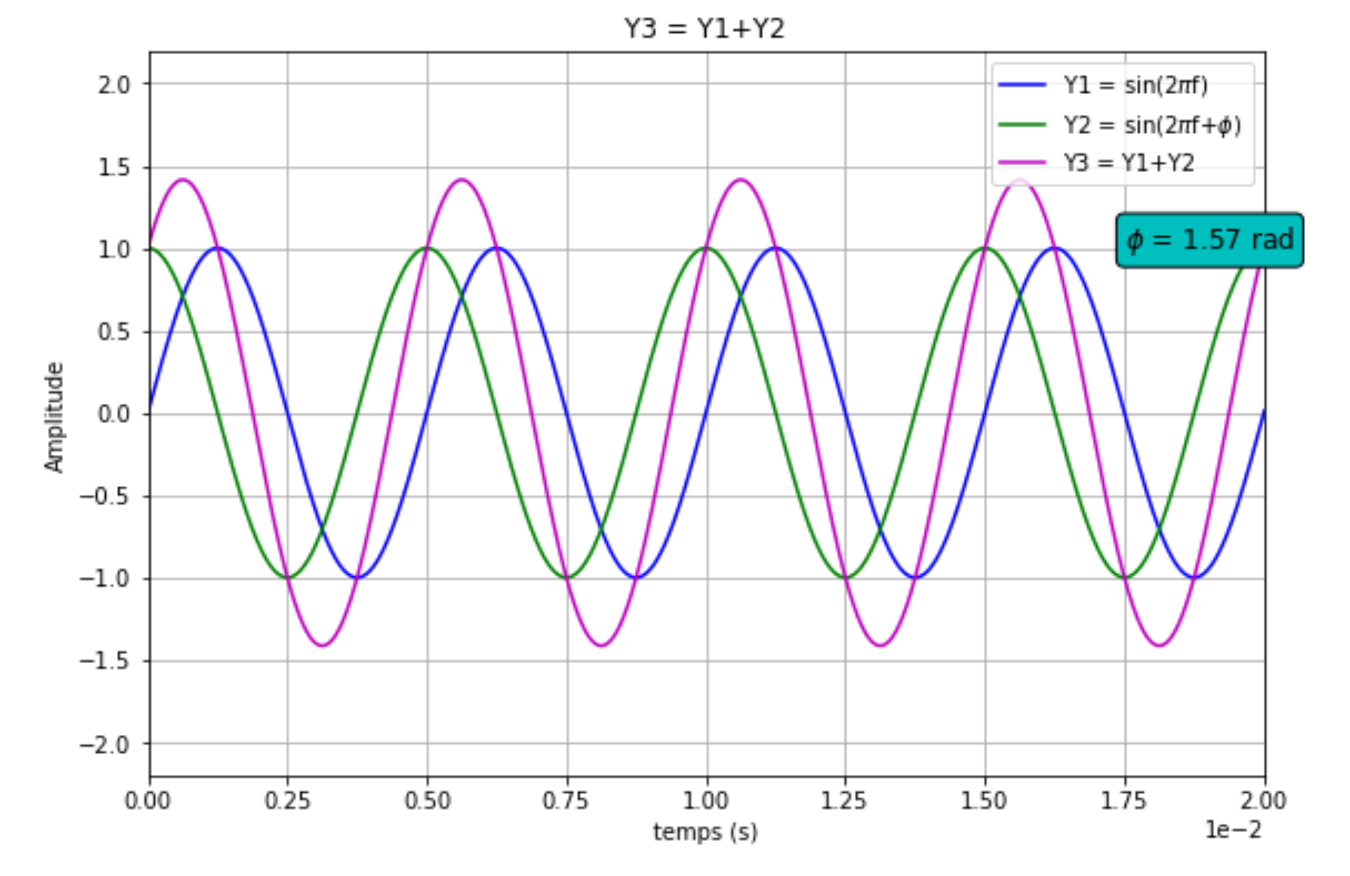
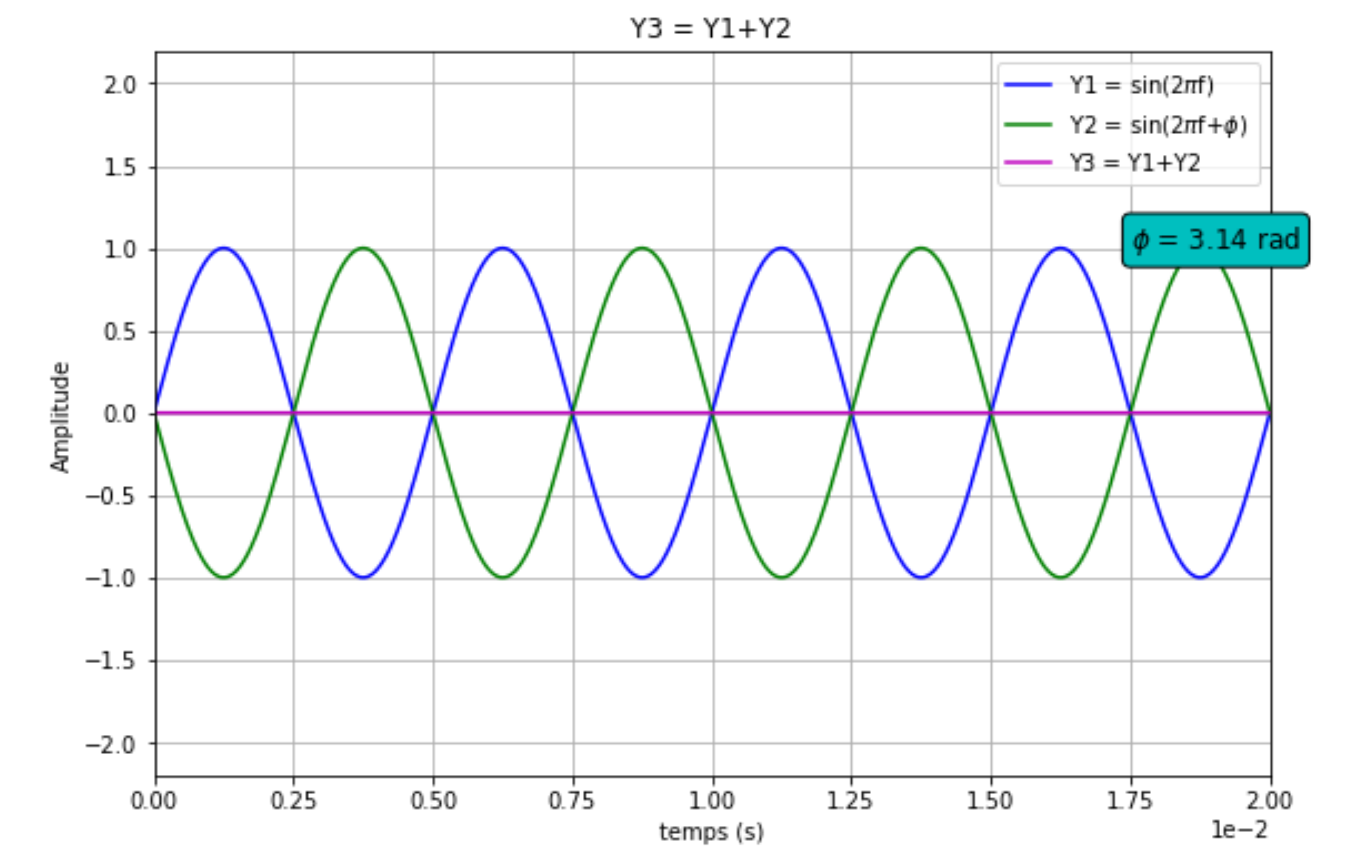
Voici quelques tracés pour des valeurs de déphasage de π/4, π/2 et π, figures 12, 13 et 14.

Figure 12.  Déphasage de π/4

Figure 13.  Déphasage de π/2

Figure 14.  Déphasage de π

Somme de deux sinus de même fréquence mais pour différentes valeurs du déphasage.

Nous allons utiliser la bibliothèque Pygame et ses différents modules afin de pouvoir jouer les sons dans le programme. Il est nécessiare de l'installer puis de l'appeler dans l'espace de travail, figures 15 et 16(avec Jupyter Notebook).

Figure 15.  Installation et appel de la bibliothèque Pygame

Figure 16.  Installation du module wave

Dans cette partie, puisqu'on s'intéresse à des fichiers sonores, on va redéfinir les signaux Y1, et Y2 à l'aide d'attributs de formats sons typiques pour pouvoir les lire à l'aide de n'importe quel lecteur (on utilise ici le format "wave").

On supprime les variables stockées dans l'espace de travail avec la fonction clear.

On utilise désormais une fréquence d'échantillonnage de 44 100 Hz pour définir Y1 et Y2, figure 17. On choisit une durée des sons de 4 secondes.

Figure 17.  Définition des signaux Y1, Y2 et Y3 avec une fréquence d'échantillonnage de 44 100 Hz

On peut vérifier que le nombre de points dans le vecteur Y1 (et donc pour les autres aussi) correspond bien au nombre d'échantillons présents dans un signal de 4 secondes à 44 110 Hz, figure 18.

La fonction len renseigne sur la taille (lenght) d'un vecteur.

Figure 18.  Instructions pour l'affichage du nombre d'échantillons d'un signal de 4 s échatillonné à 44 110 Hz et de la longueur du vecteur Y1

Le code renvoie les valeurs suivantes, figure 19.

Figure 19.  Affichage des valeurs correspondant au code figure 18

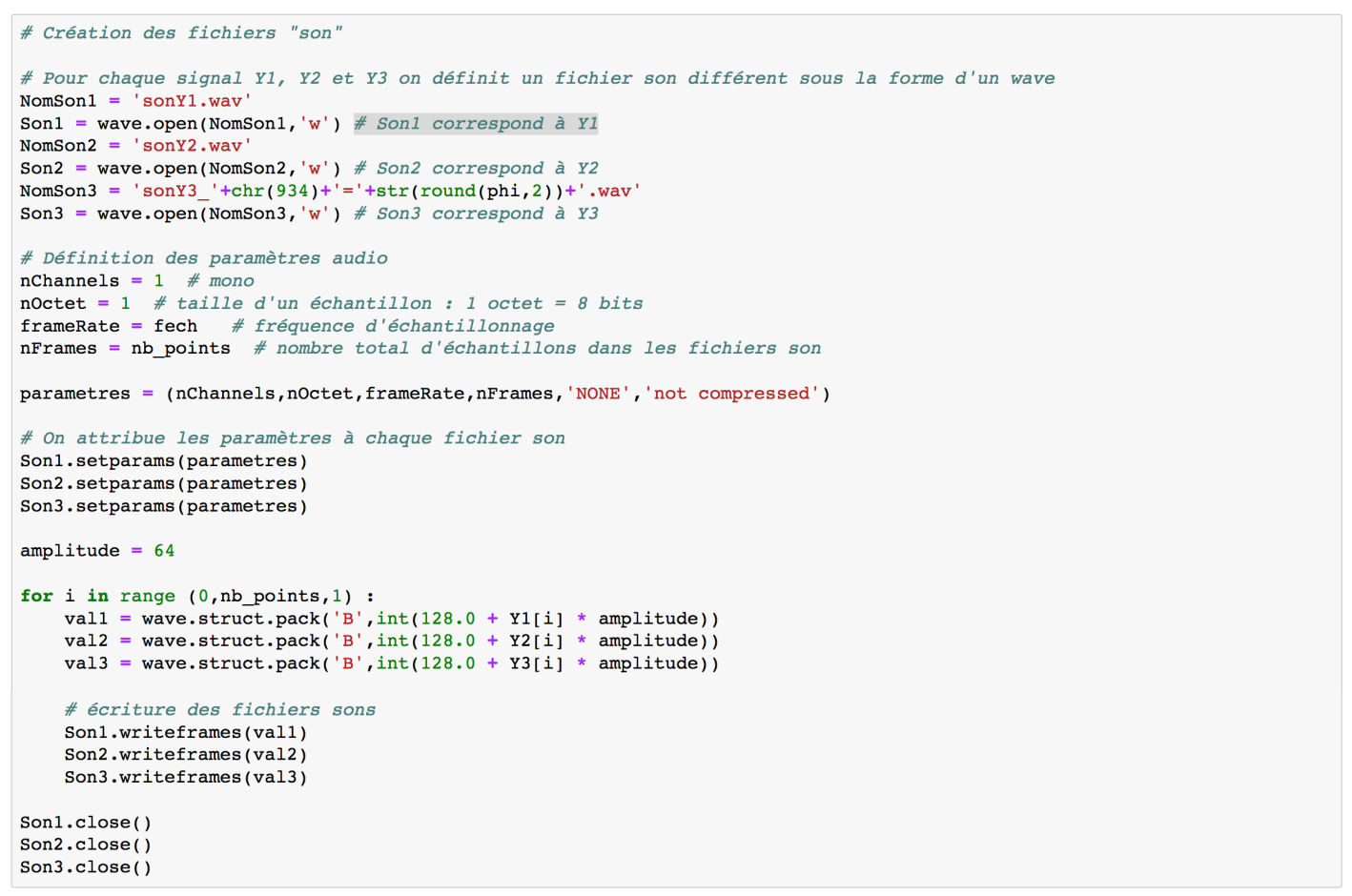
On va maintenant créer les fichiers sons à l'aide des vecteurs Y1, Y2 et Y3, figure 20.

Pour chaque signal on définit un nom de fichier au format wave ('wav') à l'aide de la fonction wave.open(...,'wb'), où 'wb' correspond à une écriture sous forme binaire (write binary).

Il est ensuite nécessaire de renseigner les paramètres audio utilisés. Dans le cadre de notre exemple, la création d'un signal 'mono' suffit (ce qui implique que tous les échantillons du signal Y1 correspondront à une seule voie. Attention à l'utilisation de stereo qui sépare en deux les éléments du vecteur).

On code chaque signal sur 8 bits = 1 octet.

On indique ensuite la fréquence d'échantillonnage (frameRate) et le nombre total d'échantillons (nFrames) dans chaque fichier son.

Tous les paramètres sont rassemblés dans l'objet "parametres", ils sont obligatoires pour la fonction setparams. Les autres champs correspondent au type de compression (comptype = "NONE") et au nom de la compression (compname = "not compressed"). Ici nous n'appliquons aucune compression.

Figure 20.  Création des fichiers sons correspondants au signaux Y1, Y2 et Y3

Chaque valeur des vecteurs Y1, Y2 et Y3 sera convertie en binaire pour créer les fichiers wave à l'aide d'une boucle for qui s'incrémente d'un pas sur toute la longueur des vecteurs ("nb_points").

Boucle for - Attention !

Avec un format d'échantillonnage sur 8 bits, les données ont des valeurs comprises entre 0 et 255, avec une valeur moyenne autour de 128. Il est alors nécessaire de faire osciller la sinusoïde autour de cette valeur moyenne ("128 + Y…"). En ce qui concerne l'amplitude, il faut garder en tête que, lorsque le déphasage entre Y1 et Y2 sera nul, l'amplitude de Y3 sera alors le double de Y1 et Y2. Donc il est nécessaire de multiplier au maximum l'amplitude par 64 (128/2) lorsqu'on travaille sur 8 bits.

La fonction struct.pack(format, values...) premet de créer un objet binaire à partir des données rentrées entre les paranthèses (sous le format d'entiers 'B').

Les valeurs (val1), pour le Son1 représentant Y1, correspondront donc à la partie entière de l'onde sinusoïdale renormalisée en 8 bits.

La lecture des sons dans python est réalisée avec l'outil "mixer" de pygame, tableau 1. Dan un premier temps on initialise les paramètres du mixer de son en renseignant la fréquence d'échantillonnage utilisée. Puis on indique le nom du fichier à jouer.

Dans le code proposé, on a créé 3 instructions à compiler indépendamment afin d'entendre les sons correspondants aux trois signaux Y1, Y2 et Y3.

Tableau 1.  Instructions pour la lecture des fichiers "wav"

On ouvre les fichiers sons créés précédemment dans le logiciel Audacity (ou n'importe quel autre lecteur), figures 21, 22 et 23.

On retrouve bien, pour les signaux correspondants à Y1 et Y2, une fréquence de 200Hz et une amplitude comprise entre [-0,5 ; 0,5].

L'amplitude du signal correspondant à Y3 est nulle ou quasiment (dû aux résidus du calcul numérique.)

Figure 21.  Zoom sur le signal 'sonY1.wav'

Figure 22.  Zoom sur le signal 'sonY2.wav'

Figure 23.  Zoom sur le signal 'sonY3_Φ=3.14.wav'

Lecture des trois signaux sonores sous Audacity, ici le déphasage est égal à π

Pour un déphasage nul ou égal à 2π, l'amplitude du signal Y3 est bien comprise entre [-1 ; 1], figure 24. La fréquence est bien de 200 Hz.

Figure 24.  Zoom sur le signal 'sonY3_Φ=0.wav', le déphasage est ici nul

Finalement, à l'aide d'une analyse numérique, nous venons de retrouver que la somme de deux signaux sinusoïdaux de même fréquence mais de phase différente donne un signal de même fréquence que les 2 autres signaux mais d'amplitude variable, selon la valeur du déphasage.