Activer le mode zen
Ressource au format PDF
Classification
Traitement du signal et étude des réseaux : application à l'étude du système de vélos en libre-service à Lyon
29/02/2016
Résumé
Cet article illustre l'utilisation d'outils physiques pour l'analyse des déplacements urbains. Ce travail est tiré d'une thèse financée par la Région Rhône-Alpes (Programmes ARC5 et ARC6) et l'application au système de vélos en libre-service vélo'v s'est fait dans le cadre de l'ANR Vélinnov.
Ce travail a été récompensé par le prix de thèse de la Chaire Abertis 2016, dont l'ambition est de développer les activités de formation et de recherche dans la gestion des infrastructures de transport.
Table des matières
1. Le système vélo'v
1.1 Qu'est ce qu'un système de vélos en libre-service ?
Les systèmes de partage de vélos sont devenus ces dix dernières années des éléments incontournables dans les politiques de transport urbain, comme en témoigne l'explosion récente du nombre de vélos en circulation dans les grandes villes du globe. En proposant un accès abordable au vélo, cela permet de participer activement à la mise en place d'alternative aux véhicules motorisés pour les déplacements urbains et de contribuer à la réduction de la pollution de l'air, du niveau de bruit et des problèmes de congestion touchant les grandes métropoles mondiales. Une des clés du succès du partage de vélos est sa simplicité d'utilisation. Dans la majorité des systèmes, l'utilisateur a la possibilité de retirer ou de déposer un vélo dans une des nombreuses stations réparties sur toute la ville, le tout de manière entièrement automatisée.
Vélo'v est le système de vélos en libre-service (VLS) mis en place dans la ville de Lyon et de Villeurbanne à partir de mai 2005 par la communauté urbaine du Grand Lyon (figure 1). Le système comprend actuellement 348 stations, avec environ 4000 vélos en circulation. En 2014, plus de 8,3 millions de locations ont été réalisées par les 58 000 abonnés annuels et les 773 410 utilisateurs ponctuels utilisant le système sur une journée ou une semaine. Chaque vélo est partagé en moyenne 6 fois par jour, ce qui en fait un des systèmes les plus actifs d'Europe, et un des premiers succès des systèmes VLS. Il est en effet le premier système de grande envergure à avoir été mis en place dans le monde, et a notamment ouvert la voie à la mise en service de systèmes de plus grande envergure, comme le système Vélib à Paris.
Les vélos sont disponibles à la location tandis que les bornettes libres peuvent accueillir des vélos. La borne d'accueil permet de s'abonner et de s'identifier afin de louer un vélo et consulter son compte. Les bornettes libres peuvent accueillir des vélos. (Image source: Bonifas - Wikimedia Commons').
1.2 Comment l'analyse de données peut apporter un éclairage nouveau sur ce système de transport ?
Comme tout système informatisé, les systèmes de vélos en libre-serice génèrent des données volumineuses et complexes, dont l'utilisation est essentiellement limitée à la gestion et à l'exploitation du système. Les mouvements effectués par les usagers du système peuvent pourtant fournir des informations précieuses sur de nombreux aspects de la vie urbaine, par exemple sur la dynamique temporelle et spatiale des déplacements dans la ville, sur la place du vélo parmi les autres modes de transport, ou encore sur la répartition des inégalités territoriales et sociales dans l'espace géographique. Ce mouvement global d'extraction de connaissance dans des corpus de données numériques s'intègre au concept plus général des Big Data, ou datamasse.
L'analyse et l'interprétation de ces données ont mené à des collaborations fructueuses entre chercheurs de différentes disciplines, permettant par exemple de spatialiser l'activité vélo'v dans l'espace géographique lyonnais en fonction de considérations socio-économiques. Une autre approche a été de mettre en oeuvre des classifications d'usagers, principaux acteurs des systèmes VLS. En établissant des profils d'utilisation basés sur leur pratique du vélo'v, il est possible d'établir une différentiation entre les motifs temporels des abonnés journaliers, hebdomadaires et annuels, et de mettre en place une comparaison entre les différents types d'usagers et les différents modes d'utilisation du partage de vélos.
1.3 En quoi vélo'v amène à considérer de nouvelles méthodologies ?
Les systèmes de vélos en libre-service peuvent également se représenter sous la forme d'un réseau, en considérant les entités comme les stations et les liens comme des flux de vélos. Ces données relationnelles peuvent tout d'abord être considérées soit comme des données tabulaires statiques, soit comme des données dynamiques agrégées en séries temporelles, permettant l'utilisation des techniques usuelles en fouille de données telles que la classification ou la régression linéaire. Néanmoins, si l'on veut pleinement exploiter les dimensions spatiale et temporelle des données, il semble essentiel de considérer à la fois la structure en réseau et la dynamique des relations, amenant ainsi à étudier des réseaux temporels, c'est-à-dire des réseaux dont la structure évolue au cours du temps.
Le manque d'outils adaptés pour étudier ces objets appelle à de nouvelles méthodes, dont le développement est la motivation des travaux présentés par la suite. La méthode proposée se base sur le parallèle entre l'analyse de réseaux temporels et de signaux temporels, objets d'étude de la discipline du traitement du signal. Les similitudes dans la description de l'évolution d'un réseau temporel et celle d'un signal permettent de considérer une dualité entre ces deux types d'objets. Ainsi, l'analyse dans le domaine des signaux, à l'aide d'outils de traitement du signal bien établis, permet de caractériser le réseau temporel correspondant.
La complexité de ces données nécessite d'adopter une approche multidisciplinaire incluant les sciences exactes et les sciences huamines. Ces travaux s'intègrent ainsi pleinement dans la thématique émergente des réseaux complexes.
Références
2. Analyse de données sur les réseaux : approche par le traitement du signal
L'étude des réseaux complexes met en jeu de nombreuses disciplines des sciences exactes : la théorie des graphes permet de modéliser les réseaux à l'aide d'objets mathématiques, les graphes. L'informatique permet de mettre en place des algorithmes efficaces pour traiter des données en grande quantité. La physique apporte des concepts de méthode innovants, facilement adaptables aux réseaux. Enfin, l'analyse de réseaux complexes n'est pas possible sans considérer la discipline dans laquelle les données sont ancrées, et qui peut aller de la biologie à la psychologie, en passant par le transport, la sociologie ou encore l'histoire.
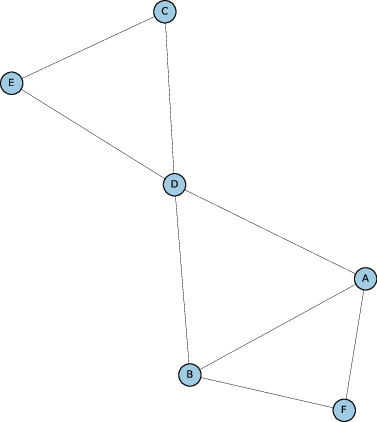
La théorie des graphes est un sous-domaine des mathématiques : un graphe est un objet mathématique qui consiste en un ensemble de noeuds (aussi appelés sommets), reliés par des liens. Un graphe est dit simple s'il ne contient pas de boucles, c'est-à-dire des liens dont les deux extrémités sont le même noeud, ni de liens multiples, c'est-à-dire des liens reliant la même paire de noeuds. Par la suite, nous considérerons uniquement des graphes simples.
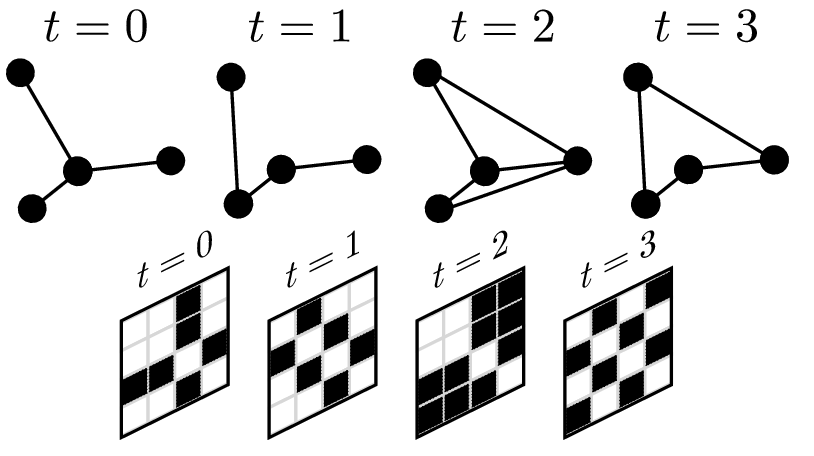
Une représentation classique d'un graphe consiste à dessiner les noeuds comme des points, et les liens par des traits entre les points, figure 2.
Deux variantes sont fréquentes dans l'analyse de graphe :
- Les liens du graphe peuvent être pondérés, en leur assignant une valeur représentant un degré de proximité ou au contraire, une dissimilarité : le graphe est dit pondéré ;
- Un lien peut exister dans une direction mais pas dans l'autre : le graphe est dit dirigé.
La théorie des réseaux se différencie de la théorie des graphes en ceci qu'elle se concentre plus particulièrement sur les systèmes physiques pouvant se représenter sous la forme de graphes. Elle fait ainsi le lien entre la théorie des graphes et d'autres disciplines, comme la physique, l'informatique, la biologie, la sociologie ou l'économie, à la fois par l'étude de données issues de ces domaines (réseaux sociaux, réseau Internet, etc.) mais également par l'utilisation d'outils extérieurs à la théorie des graphes, comme ceux de la mécanique statistique. De nombreux outils ont été développés pour définir des mesures du réseau, comme par exemple la détection de communautés. (On pourra consulter la référence « Community detection in graphs », de S. Fortunato.)
3. Traitement du signal
Le traitement du signal est né des domaines de l'électronique et de l'automatique avec pour but initial de répondre aux problématiques liées à l'utilisation des signaux dans des systèmes. (Voir l'article Traitement du signal et des images : description et applications en 3 questions à Pierre Borgnat).
3.1 Transformée de Fourier discrète de signaux réels
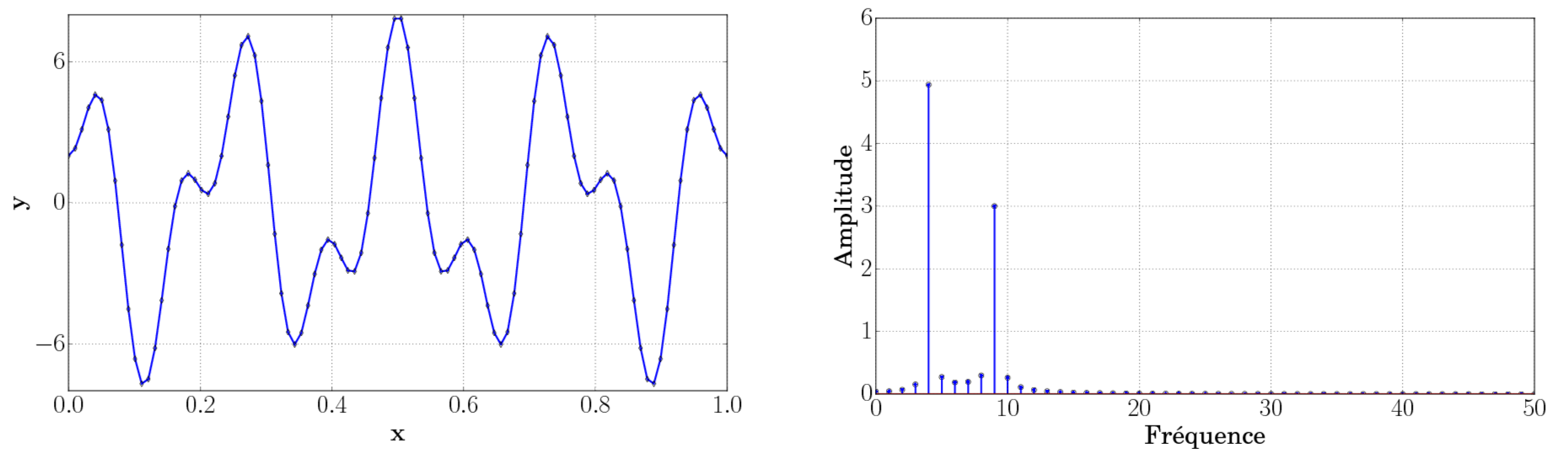
La transformée de Fourier discrète est une opération qui permet de représenter un signal discret réel en composantes fréquentielles, c'est-à-dire de représenter un signal comme une somme d'oscillations harmoniques, figure 3.
L'amplitude et l'énergie de la transformée de Fourier d'un signal donnent des indications sur l'importance d'une fréquence dans le signal par rapport aux autres, alors que la phase permet de caractériser le déphasage entre les oscillations harmoniques.
3.2 Traitement du signal et réseaux
Naturellement, le développement récent de la théorie des réseaux, et plus généralement l'apparition de données massives sous la forme de réseaux, a ouvert la voie vers une extension du traitement du signal à l'étude des réseaux. En complément de la méthode proposée dans cet article, on peut également mentionner l'émergence du domaine du traitement du signal sur graphe, dont l'objectif est de transposer les notions et outils du traitement du signal, classiquement défini dans un espace régulier, vers le domaine des graphes. À la différence d'un signal défini sur une topologie régulière, par exemple un signal échantillonné dans le temps ou défini sur une grille, un signal défini sur un graphe consiste à assigner à chacun des noeuds du graphe un scalaire, et à utiliser la topologie du graphe comme support. De nombreux travaux sur la généralisation des concepts du traitement du signal classique ont ainsi éclos à partir de cette définition, que ce soit les opérations usuelles telles que la convolution, la translation, la modulation ou le filtrage, mais également des outils plus complexes comme la définition d'un principe d'incertitude, les ondelettes, la décomposition en modes empiriques ou la stationnarité.
Références
- Réseaux et signal : des outils de traitement du signal pour l'analyse des réseaux, manuscrit de thèse de N. Tremblay.
3.3 Comment transformer des réseaux en signaux ?
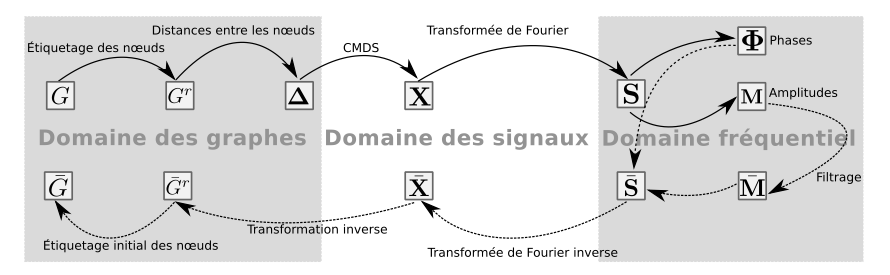
Une méthode de transformation de réseaux en signaux a été proposée (figure 4), basée sur une technique classique de statistique, le positionnement multidimensionnel classique (ou classical multidimensionel scaling (CMDS) en anglais) : les noeuds du graphe sont représentés comme un ensemble de points dans un espace euclidien, dans lequel les relations entre les noeuds sont codées par les distances entre les points. Les signaux contiennent l'information complète sur la structure du graphe.
La transformation de graphes en signaux se réalise simplement en définissant une matrice de distance entre les noeuds du graphe.
3.4 Illustrations
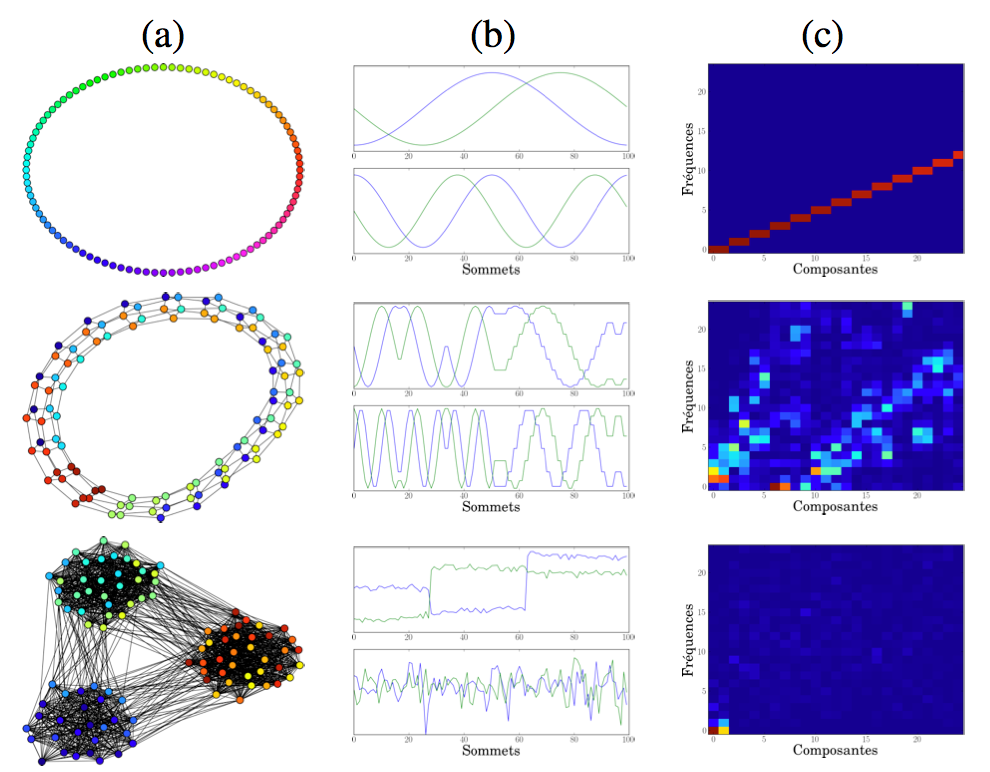
Colonnes : (a) représentation du graphe. (b) Les 4 premières composantes associées au graphe. Composantes 1 (bleu) et 2 (vert) sur le graphe du haut et composantes 3 (bleu) et 4 (vert) sur le graphe du dessous. (c) Énergie en fonction de la composante et de la fréquence pour les 25 premières composantes et 25 premières fréquences, en code couleur. Image obtenue avec Python/Numpy/Matplotlib.
La figure 5 propose trois exemples de graphes de 100 noeuds. Pour chaque exemple, la colonne (a) présente un aperçu du graphe, la colonne (b) affiche les quatre premières composantes de la collection de signaux obtenue après transformation. On remarque que la présence de régularité dans le graphe se traduit par des sinusoïdes alors que la présence de communautés donne des signaux avec des paliers correspondants aux communautés du graphe. La colonne (c) représente l’énergie de chaque fréquence pour chaque composante.
Pour aller plus loin on pourra consulter l'article Transformation de graphes dynamiques en séries temporelles non stationnaires, 24ème Colloque GRETSI sur le Traitement du Signal et des Images, Brest, 3-6 septembre 2013.
3.5 Extension aux réseaux temporels
Dans la nature, le temps est un paramètre fondamental dans la réalisation des processus complexes. Il est en effet difficile d'imaginer décrire un système, comprendre ses mécanismes et prédire son comportement sans prendre en compte la dynamique temporelle de ce système, et ceci quelle que soit sa nature.
L'importance du temps interroge les chercheurs de toutes les disciplines et s'il est complexe de le caractériser en tant que tel, sa prise en compte est primordiale dans des domaines aussi variés que l'épidémiologie, la biologie, l'économie, les télécommunications ou la musique. Les systèmes se représentant sous la forme de réseaux, c'est-à-dire comme un ensemble de relations entre des entités, n'échappent pas à cet effet du temps, et la compréhension de leur fonctionnement nécessite de considérer la dynamique de ces relations. La théorie des réseaux, dont les outils sont pour la plupart adaptés à des représentations statiques, nécessitent ainsi une extension pour considérer cette dynamique.
L'analyse de l'évolution de grandeurs caractéristiques du graphe, comme le nombre de liens, permet de faire ressortir des mouvements périodiques ou d'étudier la stationnarité du graphe. Cette approche pose néanmoins le problème du choix des mesures qui sont limitées pour assurer une bonne représentativité la structure du graphe. Une solution intermédiaire pour pallier ce problème consiste à décrire le réseau non plus par un graphe ou par des mesures, mais par la collection de signaux obtenue en utilisant la méthode proposée ci-dessus. Ces signaux, qui représentent exactement la structure du réseau, peuvent ainsi se substituer au graphe et permettent l'utilisation des techniques du traitement du signal.
La Figure 6 résume schématiquement un réseau temporel à 4 noeuds sous la forme d’une séquence de graphes et d’un tenseur d’adjacence correspondant.
3.6 Comment simplifier les réseaux temporels ? - Application aux données vélo'v
L'animation, figure 7, présente l'évolution du réseau temporel d'utilisation des vélos entre 5h00 et 9h00, le matin un jour de semaine. Les points rouges représentent les vélos et leur parcourt potentiel, les traits bleus relient deux noeuds en communication, c'est-à-dire un noeud (une station) où le vélo est emprunté et un noeud (une autre station) où ce même vélo est rendu.
Grâce à la représentation sous la forme de signaux, il est envisageable d'utiliser des techniques classiques de simplification des données. Parmi elles, la factorisation en matrices non-négatives permet de décomposer le réseau temporel en un ensemble de motifs, couplés à des coefficients donnant les périodes d'activation de ces motifs au cours du temps.
Cette approche est illustrée sur le réseau temporel vélo'v, obtenu à partir des données de déplacements moyennés sur la semaine. Les motifs obtenus vont décrire les schémas de déplacement dans la ville, alors que les périodes d'activation indiquent quand ce schéma de déplacement est présent.
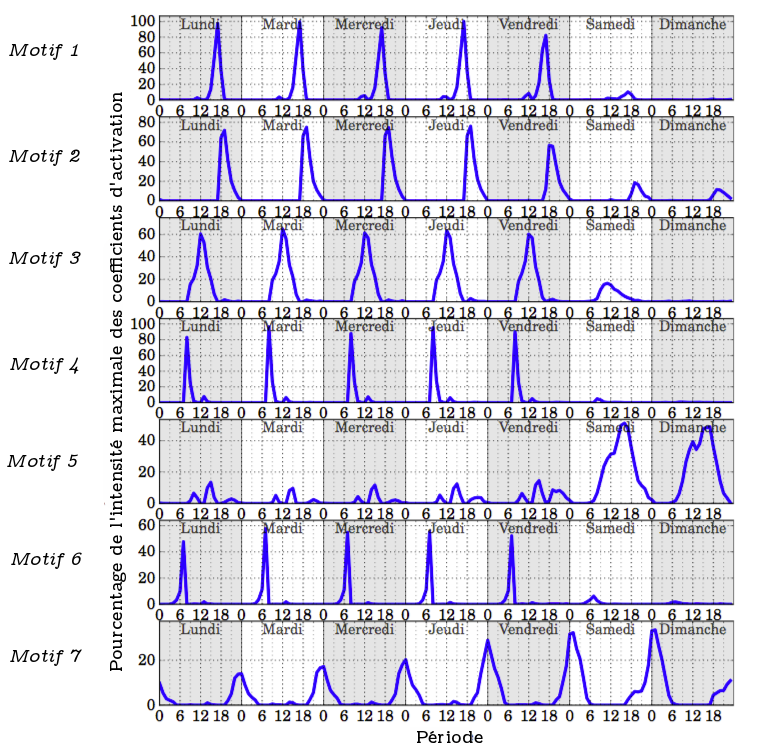
La figure 8 affiche pour chacun des motifs les coefficients d'activation pour chaque intervalle au cours de la semaine. Les pics d'intensité permettent de classer les motifs suivant deux critères : la période de la journée (matin, midi, après-midi, soirée et nuit) et le type de jour (jour de semaine ou week-end).
- Motif 1 : semaine - après-midi (17h)
- Motif 2 : semaine - début de soirée (18h-19h)
- Motif 3 : semaine - midi (11h-14h)
- Motif 4 : semaine - matin (8h)
- Motif 5 : week-end - journée
- Motif 6 : semaine - matin (7h)
- Motif 7 : nuit (23h-3h)
La description temporelle des motifs montre que la factorisation en matrice non-négatives extrait de manière automatique les périodes pertinentes d'un point de vue socio-économique, à savoir les pics d'activité du système.
On peut noter que la modulation du coefficient d'activation permet d'associer un même comportement avec des variations dans l'intensité de ce comportement. Par exemple, le motif 7 exprime une activité présente la nuit entre 23h et 3h du matin, similaire pour chaque jour de la semaine, mais avec une intensité plus forte le jeudi, vendredi et samedi, jours où l'activité nocturne est plus intense.
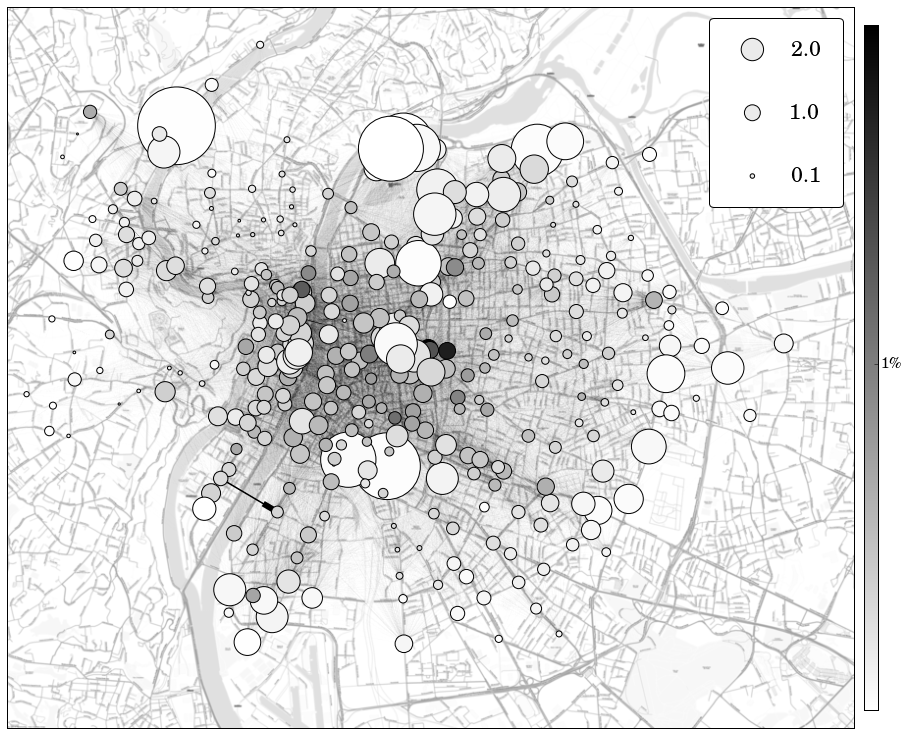
Les noeuds correspondent aux stations. La couleur des noeuds indique le degré sortant du noeud sur une échelle de blanc à noir, représentant un pourcentage de l’activité totale. La taille des nœuds indique le ratio entre degré entrant et degré sortant. Les arcs entre les noeuds sont représentés et leur épaisseur est proportionnelle au poids associé à chaque arc. Image obtenue avec Python/Numpy/Matplotlib.
La figure 9 présente le réseau correspondant au motif 4, principalement actif le matin les jours de semaine. L'étude de ce réseau permet de retrouver des éléments déjà connus sur les rythmes matinaux dans la ville de Lyon. Tout d'abord, l'activité est concentrée sur quelques stations dans des zones spécifiques telles que Part-Dieu, regroupant la gare, un centre commercial et le quartier des affaires, ainsi que dans le centre de la presqu'île.
Les comportements des stations sont également cohérents avec les analyses socio-économiques déjà réalisées : les stations qui se remplissent sont situées autour des campus (La Doua, Université Jean-Moulin, etc.) ou dans des zones à forte activité commerciale. Parallèlement, les stations qui se vident sont situées dans les zones résidentielles (8ème arrondissement, ouest du 3ème arrondissement, etc.) et les zones en altitude (Croix-Rousse, Fourvière). Ce réseau souligne ainsi la disparité géographique des déplacements urbains dans une période de grande activité.
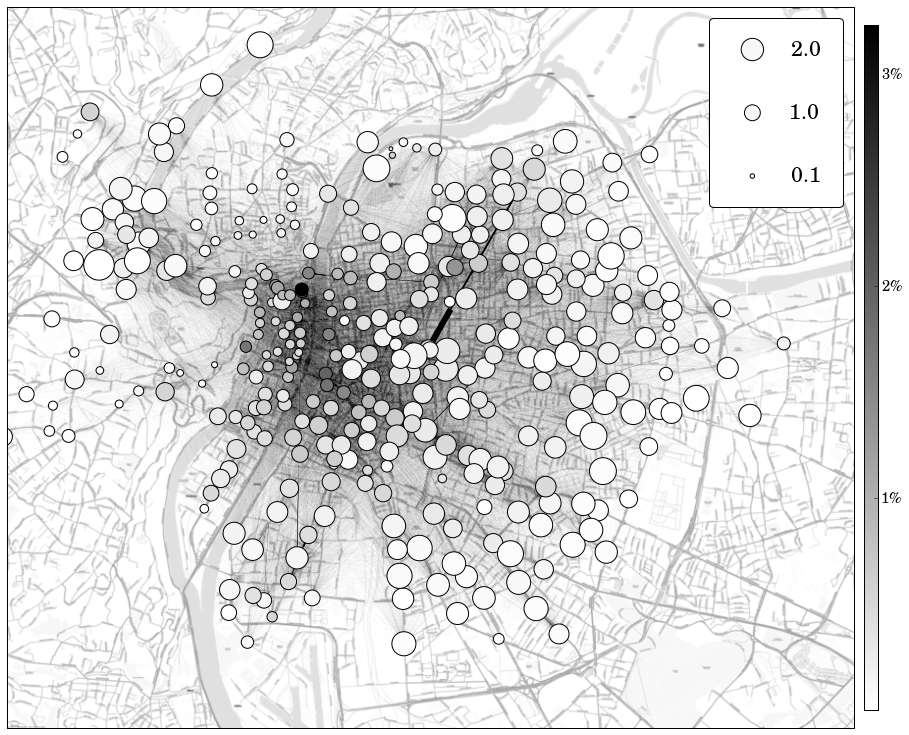
Les noeuds correspondent aux stations. La couleur des noeuds indique le degré sortant du noeud sur une échelle de blanc à noir, représentant un pourcentage de l’activité totale. La taille des noeuds indique le ratio entre degré entrant et degré sortant. Les arcs entre les noeuds sont représentés et leur épaisseur est proportionnelle au poids associé à chaque arc. Image obtenue avec Python/Numpy/Matplotlib.
La Figure 10 correspond au motif 7, dont les coefficients d’activation présentent des pics d’intensité la nuit entre 23h et 3h du matin chaque jour de la semaine. Si l’activité est concentrée comme attendu autour des zones dynamiques telles que les quartiers de l’Opéra, de Saint Jean ou de la Guillotière, regroupant de nombreux bars et restaurants, les stations situées au centre sont enclines à se vider au profit de celles situées à la périphérie de la ville. Cela souligne ainsi l’usage du vélo comme moyen de transport alternatif lorsque les métros et bus ne fonctionnent plus.
Conclusion
À travers l'exemple du système vélo'v, il a été mis en évidence à la fois comment des problèmes concrets issus des domaines des sciences humaines permettent de réfléchir à des méthodes innovantes d'analyse de données, ainsi que l'intérêt d'utiliser des méthodes quantitaves, en l'occurence ici la théorie des réseaux et le traitement du signal, pour apporter des éléments nouveaux à la compréhension de systèmes socio-économiques. Ces travaux confirment ainsi la pertinence de considérer des approches interdisciplinaires pour l'étude des systèmes complexes.
Ce travail est tiré d'une thèse financée par la Région Rhône-Alpes (Programmes ARC5 et ARC6). L'application au système de vélos en libre-service vélo'v s'est fait dans le cadre de l'ANR Vélinnov, le travail a été réalisé au Laboratoire de Physique de l'ENS de Lyon.
Ce travail a été récompensé par le prix de thèse de la Chaire Abertis 2016, dont l'ambition est de développer les activités de formation et de recherche dans la gestion des infrastructures de transport.
Pour citer cet article :
Traitement du signal et étude des réseaux : application à l'étude du système de vélos en libre-service à Lyon, Hamon, février 2016. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/signal-reseau-velo.xml