Activer le mode zen
Ressource au format PDF
Mots-clés
- relativité restreinte
- relativité générale
- paradoxe des jumeaux
Classification
Relativité et vitesse de la lumière
18/09/2003
Résumé
Présentation de la relativité restreinte : historique, cadre théorique, conséquences et paradoxes dont le célèbre « paradoxe des jumeaux ». Présentation brève de la relativité générale, en particulier de quelques changements par rapport à la relativité restreinte. Un article du dossier « La vitesse de la lumière », proposé par Gabrielle Bonnet.
Table des matières
- Introduction : relativité restreinte et relativité générale
- La relativité restreinte
- Et la relativité générale ?
Introduction : relativité restreinte et relativité générale
La relativité restreinte peut se concevoir comme une « correction » de la physique Newtonienne : cette dernière reste une approximation convenable pour décrire le comportement d'objets dont la vitesse est petite devant la vitesse c de la lumière dans le vide, la relativité restreinte n'étant nécessaire que pour décrire des situations où certaines vitesses sont suffisamment proches de c.
En général, on considère qu'un objet est "relativiste", c'est-à-dire qu'il doit être étudié en utilisant les lois de la relativité restreinte, lorsque sa vitesse v est supérieure à un dixième de la vitesse de la lumière dans le vide c, soit v > c/10 = 3,0 . 107 m/s. La correction apportée à la physique Newtonienne (aussi appelée "physique classique") est au minimum de l'ordre de 1%.
La relativité générale peut, elle aussi, sembler n'être qu'une « correction » apportée à la physique classique puisqu'elle intervient lorsque les vitesses ou les masses considérées sont très importantes (de l'ordre de celle du Soleil par exemple), mais n'apporte pas de modification perceptible à la physique de notre vie de tous les jours. Cependant, tout comme la mécanique quantique, la relativité a une portée de loin supérieure à celle que l'on pourrait attendre d'une correction aux formules habituelles de la mécanique classique : la « correction » de la relativité ébranle en effet les fondements mêmes de notre vision de l'espace et du temps.
Prenons un exemple : en relativité, deux évènements simultanés pour un observateur ne le sont plus pour un deuxième observateur en mouvement par rapport au premier.
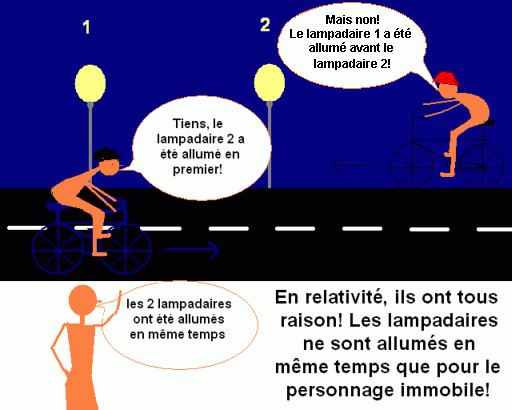
Evidemment, les bicyclettes doivent avoir une vitesse relativiste (plus de cent millions de kilomètres à l'heure) pour que ces effets soient perceptibles...
La relativité déjoue les raisonnements intuitifs et nous force à remettre en cause les évidences de la mécanique classique. La théorie de la relativité impose une véritable révolution de l'esprit, comme le fait de manière encore plus profonde la mécanique quantique.
La relativité restreinte
Historique
La relativité restreinte est le prolongement d'une idée très ancienne : celle de relativité du mouvement, adaptée pour que les lois de l'électromagnétisme de Maxwell soient valables dans tous les référentiels Galiléens.
On sait en effet depuis longtemps que les principes de base de la physique comme le principe de l'inertie, par exemple, sont valables dans tous les référentiels Galiléens. Puisque la physique est exactement la même dans deux référentiels Galiléens en mouvement l'un par rapport à l'autre, les mots "mouvement" et "immobilité" n'ont de sens que relativement à un référentiel donné et la notion d'immobilité "absolue" est à bannir.
Pourtant, lorsque les lois de l'électromagnétisme de Maxwell ont été établies et dûment vérifiées, vers la fin du 19ième siècle, il a bien fallu constater qu'en appliquant les lois de la physique classique, elles ne pouvaient pas être les mêmes dans tous les référentiels Galiléens. Les équations de Maxwell font en particulier intervenir une constante, c, qui est la vitesse de la lumière dans le vide. Par un changement de référentiel classique, si c est la vitesse de la lumière dans le vide dans un premier référentiel, et si on se place désormais dans un nouveau référentiel en translation par rapport au premier à la vitesse constante v, la lumière devrait désormais aller à la vitesse c-v si elle se déplace dans la direction et le sens de v, et à la vitesse c+v si elle se déplace dans le sens contraire.
L'expérience de Michelson et Morley, qui a montré que le déplacement de la Terre autour du Soleil ne semble pas avoir d'influence sur la vitesse de la lumière sur Terre (celle-ci reste la même dans toutes les directions), démontre qu'en dépit du raisonnement effectué plus haut, c semble bien être la même dans tous les référentiels Galiléens et les équations de Maxwell semblent bien vérifier le principe de relativité. Pour résoudre ce paradoxe apparent, il a fallu admettre que la physique classique était à modifier... C'est ainsi que fut introduite la relativité.
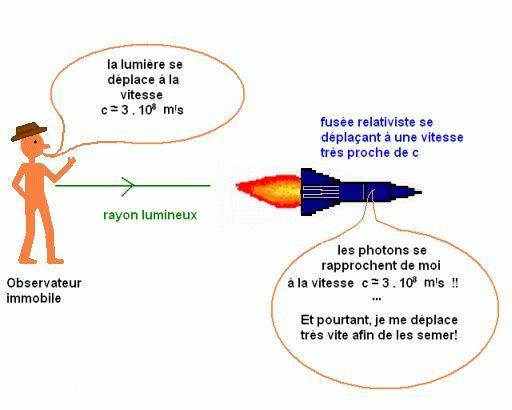
La vitesse de la lumière est la même dans tous les référentiels... Les photons vont à la même vitesse c que ce soit dans le référentiel de la fusée ou dans celui de l'observateur fixe par rapport à la Terre.
On ne peut pas dépasser la vitesse de la lumière !
Pour comprendre cette conséquence de la relativité, il suffit de se rappeler la célèbre formule E = m c2 qui décrit l'équivalence entre un objet de masse m, au repos, et la quantité d'énergie E (c est la vitesse de la lumière dans le vide). En fait, cette formule n'est pas valable pour un objet en mouvement. Pour un objet de masse m se déplaçant à la vitesse v on a :
E = γ m c2 |
où γ est le coefficient sans dimension :
γ = (1 - v2/c2)-1/2 |
à petites vitesses, cette formule, par un simple développement limité au premier ordre en v2/c2, redonne la valeur habituelle de l'énergie cinétique d'un objet en mouvement à la vitesse v qui s'additionne à l'énergie de masse au repos E = m c2 de l'objet.
On remarque que γ tend vers l'infini lorsque v s'approche de c. Ainsi, l'énergie d'un objet de masse m non nulle en mouvement à la vitesse v = c serait infinie, et, par conséquent, pour accélérer cet objet jusqu'à la vitesse de la lumière, depuis l'état de repos ou depuis un mouvement à une vitesse v < c, il faudrait lui fournir une énergie infinie.
On remarque aussi que le raisonnement précédent n'est plus valable pour une particule de masse nulle. En fait, la formule précédente est une expression indéterminée (mathématiquement parlant) si m = 0 et v = c. Ces particules de masse nulle mais se déplaçant à la vitesse de la lumière existent : l'exemple qui vient immédiatement à l'esprit est celui des photons.
Et si les photons avaient une masse ?
Jusqu'à présent, toutes les expériences indiquent que les photons n'ont pas de masse. Mais on peut imaginer que des mesures encore plus précises aboutissent à une masse non nulle des photons, même si on la sait extrêmement faible... Un tel résultat, aux effets à première vue imperceptibles, bouleverserait fortement les conceptions actuelles de la physique... En effet, dans ce cas, la vitesse de la lumière dans le vide ne serait plus comme aujourd'hui la « vitesse limite » qu'aucune particule, massique ou non, ne peut dépasser...
Énergie de masse
L'énergie fournie par les réactions nucléaires, sur Terre ou dans le Soleil, provient de l'« énergie de masse » E = m c2 : la désintégration d'un microgramme de matière, par exemple, fournit une énergie du même ordre de grandeur que l'énergie cinétique de plus de 100 tonnes lancées à 180 km/h ! La maîtrise, à des fins civiles, de la fusion nucléaire, en particulier, permettrait ainsi de résoudre les problèmes d'énergie sur Terre (sans les déchets nucléaires produits par les réactions de fission)... On en est malheureusement encore loin !
Mais comment la lumière peut-elle se déplacer à la même vitesse quel que soit l'observateur ?
Les changements de référentiel en relativité
Dans un changement de référentiel classique, si le point M a pour coordonnées x, y et z à l'instant t dans un premier référentiel d'origine O, dans un deuxième référentiel en mouvement par rapport au premier à la vitesse v, dirigée suivant (Ox), et dont l'origine O' coincide avec O à l'instant 0, les coordonnées de M seront x' = x - v t, y' = y et z' = z. Si la vitesse de M est V dans le premier référentiel, elle sera tout simplement V - v dans le deuxième.
Ces changements de référentiels peuvent sembler parfaitement naturels, et pourtant, l'expérience, tout comme le principe de relativité, nous montrent qu'ils sont faux. On doit définir un nouveau changement de référentiel qui laisse la vitesse c et l'ensemble des équations de Maxwell invariantes. Cette transformation s'appelle la transformation de Lorentz et s'écrit comme suit :
si les coordonnées d'un évènement donné sont x, y, z et t dans le premier référentiel défini plus haut, dans le deuxième référentiel ses coordonnées seront :
x' = γ (x - v t)
y' = y
z' = z
t' = γ (t - v x/c2)
On rappelle que le coefficient γ est le coefficient sans dimension : γ = (1 - v2/c2)-1/2.
Loi de composition des vitesses
Une conséquence de la transformation de Lorentz est de réviser la loi "classique" de composition des vitesses. On obtient une expression beaucoup plus compliquée, qui coïncide avec les lois habituelles pour des vitesses très inférieures à la vitesse de la lumière. On explicite ci-dessous la transformation des vitesses par changement de référentiel, ce qui montre qu'elle a perdu la simplicité de la transformation de Galilée.
Si un objet se déplace à la vitesse
V = V// + V⊥
dans un premier référentiel, dans un deuxième référentiel animé d'une vitesse v constante par rapport au premier, avec V// parallèle à v et V⊥ perpendiculaire à celle-ci, sa vitesse V' sera définie par la relation :
V' (1 - V.v/c2) = (V// - v) + V⊥ / γ
Si la norme de V vaut c, alors on a aussi V' = c ... La vitesse de la lumière est bien invariante!
Conséquences et paradoxes de la relativité restreinte
Intervalles de temps et taille des objets
On voit, d'après les équations de la transformation de Lorentz, qu'il ne se passe rien dans les directions y et z, perpendiculaires au mouvement. Par contre, il y a modification des longueurs dans le sens du mouvement, et il y a aussi (et peut-être est-ce la notion la plus difficile à accepter) modification des coordonnées temporelles de l'évènement.
Ainsi, on montre que si, dans le référentiel R1, deux évènements se produisant au même point d'un objet en mouvement à la vitesse v sont séparés par l'intervalle de temps Δ t, alors, dans le référentiel R2 dans lequel cet objet est immobile, ces deux mêmes évènements sont séparés par l'intervalle de temps Δ τ = Δ t / γ.
pour démontrer cette relation, il ne faut pas oublier que, dans le référentiel R1, l'objet est en mouvement à la vitesse v que l'on peut supposer colinéaire à l'axe (Ox). On a donc x = v t + x0 et l'équation de changement de référentiel τ = γ (t - v x/c2) donne Δ τ = γ (Δ t - v Δ x/c2) qui se réécrit Δ τ = γ Δ t (1 - v2/c2) soit Δ τ = Δ t / γ
Le temps τ, temps du référentiel dans lequel l'objet est immobile, est appelé "temps propre de l'objet".
γ vaut 1 pour v = 0 (si l'objet est immobile), dans tous les autres cas il est strictement supérieur à 1 et lorsque v tend vers c, γ tend vers l'infini. On a donc toujours, si v est non nulle, Δ τ < Δ t, le rapport entre les deux étant d'autant plus petit que v est proche de c pour s'annuler à la limite lorsque v tend vers c.
La durée écoulée est toujours moins grande dans le référentiel propre de l'objet que dans les autres référentiels.
Les tailles elles aussi sont modifiées. Ainsi, un objet de taille D dans son référentiel propre (celui dans lequel il est immobile) est de taille différente dans le référentiel dans lequel il est en mouvement (la distance entre deux points d'un objet s'obtient, comme en mécanique classique, en calculant la distance entre les positions de ces deux points au même instant). Plus précisément, dans les directions perpendiculaires au mouvement, les tailles ne sont pas modifiées, mais dans la direction du mouvement, si la dimension de l'objet était D dans son référentiel propre, elle devient D/γ dans le nouveau référentiel* . Ceci n'est pas non plus très intuitif a priori...
Pour ceux qui n'arriveraient pas à retrouver ce résultat par le calcul, voir des précisions dans la partie suivante : « les 'paradoxes' de la relativité restreinte ».
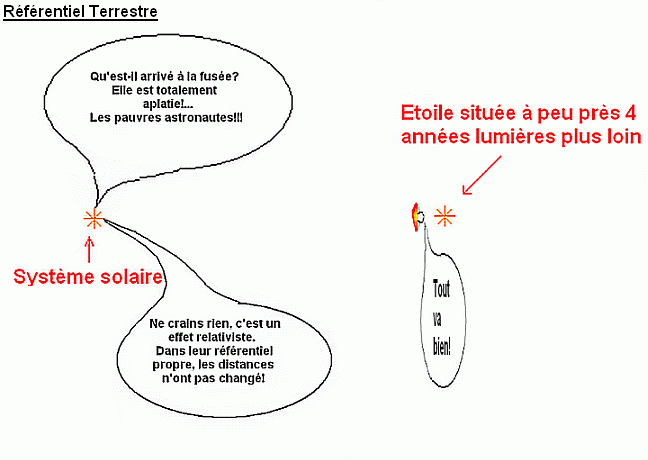
En fait, l'image de la fusée et des étoiles toutes en "taille normale" est fausse, quel que soit le référentiel dans lequel on se place... Cette image donne une idée des tailles dans le référentiel terrestre : la fusée est quasiment plate suivant la direction du mouvement. Ses autres dimensions ne sont pas modifiées.
La fusée est en mouvement dans le référentiel terrestre, sa longueur est donc plus faible que lorsqu'elle est immobile : sa taille est divisée par γ qui est ici très grand car la vitesse de la fusée est proche de c.
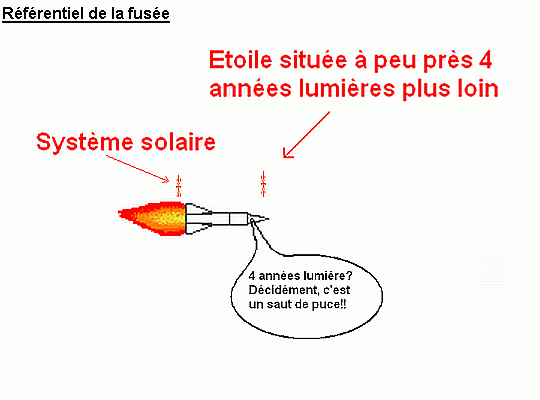
Longueurs dans le référentiel de la fusée. La fusée a la même taille qu'à l'arrêt, mais tous les objets qui étaient immobiles dans le référentiel précédent sont aplatis dans la direction du mouvement. La distance entre les deux étoiles, elle aussi, a été divisée par γ.
Dans le référentiel de la fusée, la fusée est immobile, elle est donc en taille normale. Par contre, les étoiles sont en mouvement par rapport à la fusée à une vitesse proche de c, toutes leurs dimensions sont donc divisées par γ. A la limite, si v tend vers c, γ tend vers l'infini et la distance entre les deux étoiles vaut zéro dans le référentiel de la fusée.
Les « paradoxes » de la relativité restreinte
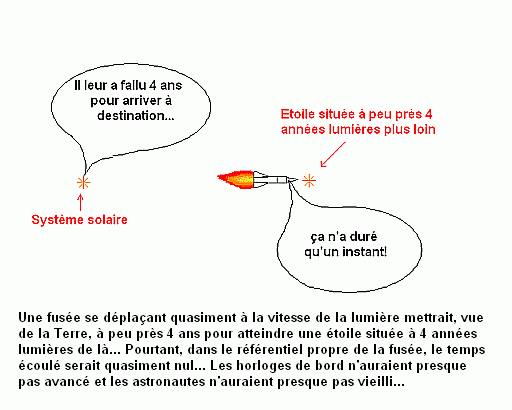
Reprenons l'histoire imaginaire de la fusée relativiste. Il semble difficile d'admettre que, dans le référentiel de la Terre, la fusée soit quasiment aplatie et mette 4 ans à atteindre sa destination tandis que dans celui de la fusée, c'est la distance entre les étoiles qui devient ridiculeusement petite (sur l'image, la fusée est même un peu plus longue, de son nez à l'extrémité des flammes qui sortent de ses tuyères, que la distance entre les étoiles!!) et le temps écoulé quasi nul.
Comment la fusée peut-elle être à la fois plus petite et plus grande que la distance entre les étoiles ?
Pour résoudre ce « paradoxe », il faut admettere que la notion de simultanéité n'est plus indépendante du référentiel. Reprenons l'histoire mise en scène plus haut : dans le référentiel de la fusée, sa pointe entre dans le système solaire de destination (évènement b) à l'instant où ses tuyères quittent notre système solaire (évènement a). La distance entre la pointe et les tuyères, à cet instant, est alors la distance entre les évènements a et b qui est, dans ce référentiel, égale à la distance entre les étoiles.
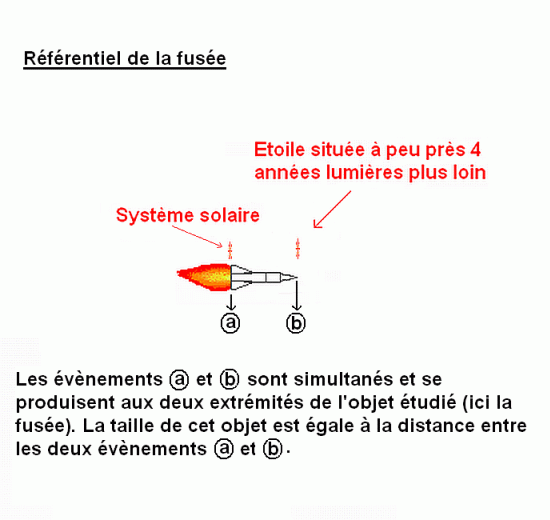
Dans le référentiel terrestre, cependant, ces deux évènements se produisent aussi, mais successivement : tout d'abord l'évènement a, puis, à peu près 4 ans après, l'évènement b. La distance entre les évènements a et b est bien égale à la distance entre les étoiles, soit, dans ce référentiel, 4 années lumière, cependant, la distance entre les évènements a et b ne représente plus la taille de la fusée, puisque a et b ne sont pas simultanés.
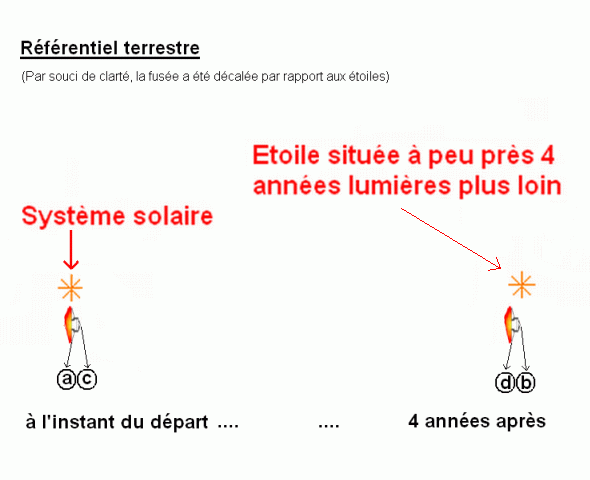
La taille de la fusée, dans ce référentiel, est la distance entre a et c, ou entre d et b, par exemple mais pas la distance entre a et b (a et c sont simultanés, de même que d et b, alors que a et b ne le sont pas).
Si on s'intéresse à l'évènement d, il s'agit de l'évènement dans lequel les tuyères de la fusée sont presque arrivées dans le système solaire de destination. Dans le référentiel de la fusée, cet évènement serait ultérieur à b : il faudrait que la fusée poursuive son voyage au-delà de l'instant où le nez de la fusée entre dans le système solaire de destination pour que les tuyères arrivent à proximité du but, dans la position qui correspond à l'évènement d.
Deux évènements simultanés dans un référentiel ne le sont pas nécessairement dans un autre. Seuls restent simultanés dans tous les référentiels 2 évènements qui se produisent au même instant et au même endroit.
Et les phases d'accélération et de décélération ?
Une fusée réelle, bien sûr, ne serait pas constamment en mouvement rectiligne et uniforme à vitesse proche de c. Il lui faudrait évidemment accélérer au départ (période pendant laquelle les astronautes verraient les distances raccourcir, et les gens restés sur Terre la fusée s'aplatir) et ralentir à l'arrivée (les objets reprendraient peu à peu leur taille "standard"). Ces périodes, cependant, pour être traitées mathématiquement, nécessitent l'introduction de la relativité générale... En relativité restreinte, en effet, on sait faire un changement de référentiel, d'un référentiel Galiléen à un autre, mais on ne sait pas traiter le cas des référentiels non galiléens...
Le « paradoxe des jumeaux »
Avec ce que nous venons de voir (si vous avez survécu jusqu'ici!), le « paradoxe des jumeaux » commence à s'éclaircir. Dans ce fameux « paradoxe », on imagine en effet que l'on envoie un jumeau dans l'espace alors que l'autre reste sur terre. Lorsque le jumeau astronaute revient sur Terre, il est plus jeune que son frère resté au sol.

Si l'on applique rapidement les lois de la relativité restreinte à ce problème, on peut penser que le voyageur, s'il s'est déplacé à la vitesse v, aura vu l'intervalle de temps Δ t / γ < Δ t s'écouler si son jumeau resté sur Terre a vu s'écouler la durée Δ t. Cependant, du point de vue du jumeau voyageur, c'est celui qui est resté sur Terre qui s'est déplacé à la vitesse v, et qui devrait donc être plus jeune... Comme les jumeaux, à l'instant initial et à l'instant final, sont au même instant au même endroit, ils le sont encore dans tous les référentiels et on ne peut pas invoquer des problèmes de simultanéité pour résoudre le problème.
Ce raisonnement est faux car, si le référentiel du jumeau resté sur Terre peut être considéré, en première approximation, comme Galiléen, celui du jumeau voyageur ne l'est pas : pour revenir à son point de départ, il ne peut pas avoir été constamment animé d'un mouvement rectiligne et uniforme, il doit forcément avoir fait demi-tour quelque part !
Le référentiel du jumeau voyageur n'étant pas Galiléen, la situation n'est pas symétrique, les deux référentiels ne sont pas équivalents.
Pour calculer le temps écoulé dans chaque référentiel, il faut faire intervenir la relativité générale. On trouve que le jumeau voyageur est effectivement plus jeune que le jumeau casanier. Cette propriété a été vérifiée expérimentalement avec des horloges atomiques extrêmement précises...
Un monde impossible ?
Si la vitesse de la lumière était nettement plus faible et si le monde, à notre échelle, était relativiste, beaucoup de choses seraient changées...

Si les objets de la vie quotidienne étaient relativistes, on aurait des problèmes dus aux fait que les notions de simultanéité ou d'ordre des évènements, sans compter les notions de durée et de longueur, dépendent du référentiel...

Heureusement, la causalité est respectée... Deux évènements reliés par un lien de causalité dans un référentiel sont reliés par le même lien dans tous les référentiels...
Cependant, même en relativité, la cause reste antérieure à l'effet dans tous les référentiels... Toutes les « évidences » de notre monde classique ne disparaissent pas, et, en particulier, les liens de causalité sont toujours respectés. Il est vrai que certains évènements peuvent se produire dans un certain ordre dans un référentiel et dans l'autre dans un autre (comme dans l'image mettant en scène les deux escargots), mais uniquement si aucun lien de causalité n'existe entre les deux.
Il est possible de démontrer cette affirmation. Pour cela, précisons tout d'abord la notion de causalité : un lien de causalité n'est possible entre deux évènements situés aux coordonnées (M,t) et (N,T) que s'il est possible à de l'information (particule, lumière, etc...) d'être transmise de M à N (ou de N à M) dans l'intervalle de temps |T-t|. Comme, ni les particules, ni l'information ne peuvent se déplacer à une vitesse supérieure à c, il faut que |MN/(T-t)| soit inférieur, ou à la limite égal à c.
Ainsi, certains évènements, s'ils sont séparés par une distance suffisamment grande (supérieure à c |T-t|), ne peuvent pas être reliés par un lien de causalité, et il se peut que l'ordre dans lequel ils se produisent diffère selon le référentiel choisi.
Si, par contre, un lien de causalité existe, montrons que l'ordre des deux évènements est le même dans tous les référentiels. Pour cela, on rappelle les équations de changement de référentiel :
T'-t' = γ (T-t) - γ v (X-x)/c2
un changement dans l'ordre des évènements (M,t) et (N,T) selon le référentiel, qui se traduirait par T'-t' < 0 et T-t > 0, n'est possible que si |X-x|/(T-t) > c2/|v| qui est lui-même supérieur ou égal à c, ce qui voudrait dire que l'information s'est propagée de l'évènement cause (M,t) à son effet (N,T) à une vitesse supérieure à celle de la lumière! En relativité, ceci est impossible !
On représente souvent les évènements qui peuvent être reliés par un lien de causalité sur un diagramme (X,T) :
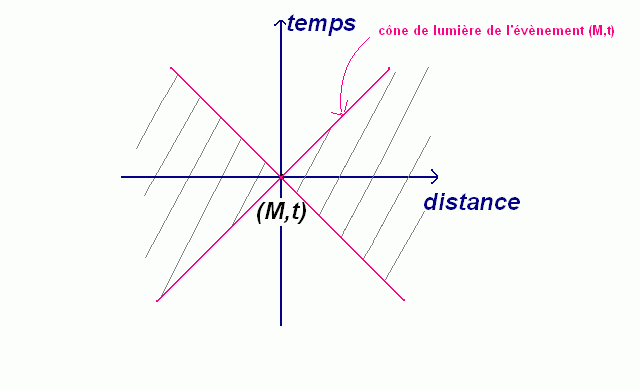
On a placé ici l'évènement (M,t) à l'origine du diagramme. La partie hachurée correspond à tous les évènements qui n'ont pas de lien de causalité avec (M,t). L'autre partie correspond aux évènements qui peuvent être, soit des causes de (M,t) (en-dessous de l'axe des abscisses), soit des conséquences (au-dessus de l'axe des abscisses). L'ensemble des évènements qui peuvent être reliés à (M,t) par un lien de causalité sont séparés par le cône contenant tous les évènements (N,T) tels que MN = c |T-t| et qui est appelé le "cône de lumière" de l'évènement (M,t).
Les évènements en-dehors du "cône de lumière" de (M,t) (caractérisés par MN > c |T-t|), dans la partie hachurée, sont totalement "invisibles" pour l'évènement (M,t).
Et la relativité générale ?
Expliquer les principes de la relativité générale, même de façon simplifiée, mériterait de longs développements. Je me contenterai ici de donner une idée minimale de quelques-uns des changements qu'apporte la relativité générale, comparativement à la relativité restreinte.
Le « paradoxe des jumeaux » nous a fait effleurer une des limites de la relativité restreinte (« special relativity » pour les anglophones). Dès que les référentiels impliqués ne sont pas des référentiels Galiléens, la relativité restreinte est insuffisante pour trouver la solution au problème. La relativité générale ne fait pas de distinction entre les référentiels Galiléens et ceux qui ne le sont pas et traîte tous ces référentiels de la même façon au sein du même formalisme mathématique. La relativité générale fait ainsi disparaître une des limites de la relativité restreinte.
Une autre des limitations de la relativité restreinte est le fait qu'elle ne prend pas bien en compte la gravitation.
Une des choses les plus remarquables, en mécanique classique, liées à la gravitation, est l'identité entre la masse inertielle et la masse pesante. La masse pesante est la grandeur qui intervient dans l'expression de la force de gravitation. Lorsqu'on écrit P = m g, la grandeur m que l'on fait intervenir est la masse pesante. L'intensité des forces de gravitation est proportionnelle à la masse pesante. Il existe aussi une autre grandeur appelée "masse", la masse inertielle, de laquelle va dépendre l'énergie cinétique que possède un objet du fait de sa vitesse et la résistance qu'il oppose à un changement de vitesse ou de direction (il est plus facile de faire dévier un chariot vide de sa course qu'un chariot plein). Lorsqu'on écrit Ec = 1/2 m v2, ou encore la troisième loi de Newton : F = m a où a est l'accélération de l'objet, la masse qui intervient est la masse inertielle. L'identité de ces deux masses n'est pas du tout "intuitive", c'est en fait un des constats les plus étonnants de la mécanique classique. La relativité générale, elle, va expliquer cette identité entre les deux masses, en identifiant la gravitation à une courbure de l'espace-temps. La gravitation n'est plus une "force" au sens classique du terme, mais un effet dérivant de la courbure de l'espace-temps. Si ce dernier est courbe, en effet, le plus court chemin entre deux points n'est plus une ligne droite mais une courbe appelée "géodésique". Les objets sont ainsi déviés au voisinage d'une masse importante parce que celle-ci courbe l'espace-temps.
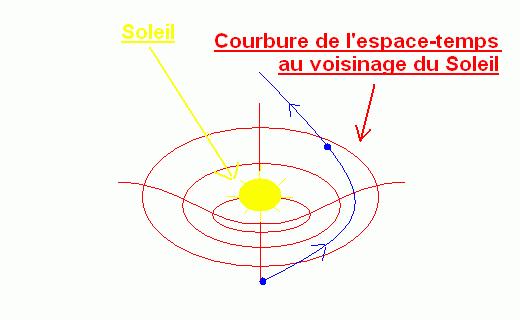
Une particule (en bleu sur l'image), initialement en mouvement rectiligne et uniforme, est déviée au voisinage du Soleil. En relativité générale, sa déviation est interprétée comme un effet de la courbure de l'espace-temps au voisinage de l'astre. La force de gravitation classique est ainsi devenue un effet "géométrique".
Cette nouvelle théorie de la gravitation a l'avantage d'expliquer naturellement l'identité entre masse pesante et masse inerte et d'intégrer la gravitation dans le cadre de la relativité.
La relativité générale a permis d'expliquer ou de prédire un certain nombre de résultats expérimentaux, comme l'avance du périhélie de Mercure, la déviation des photons au voisinage d'un corps céleste massif, l'existence des trous noirs... C'est une théorie au formalisme mathématique complexe mais dont l'existence est fondamentale pour l'astrophysique. De nos jours, certains objets de la vie courante, comme le GPS, doivent désormais tenir compte des effets relativistes...
La relativité restreinte et la relativité générale, avec la mécanique quantique, ont été pour le vingtième siècle de véritables révolutions de l'esprit.
Tous les raisonnements et les dessins qui ont été faits dans cet article, même lorsqu'on a fait s'exprimer des personnages, montrent les tailles, distances et durées réelles dans le référentiel considéré. On ne s'est pas préoccupé par contre des tailles, distances et intervalles de temps qui peuvent être perçus par l'observateur, et qui diffèrent des grandeurs réelles à cause du temps non nul que met la lumière pour arriver à l'observateur. Ceci sort du cadre de cet article mais le lecteur averti pourra s'amuser à faire les calculs correspondants pour se faire une idée de la différence entre ce que l'observateur voit et la réalité.
Article suivant : « Plus vite que la lumière ? ».
Article précédent : « Indices optiques : dérivation à partir des équations de Maxwell, signification physique, expression ».
Dossier : « La vitesse de la lumière ».
Pour citer cet article :
Relativité et vitesse de la lumière, Gabrielle Bonnet, septembre 2003. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/relat.xml




