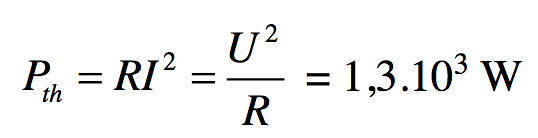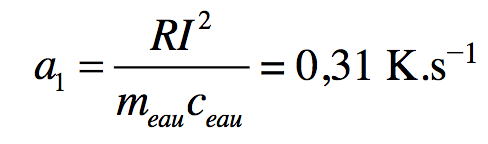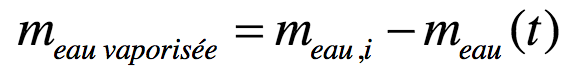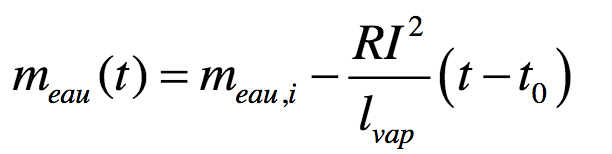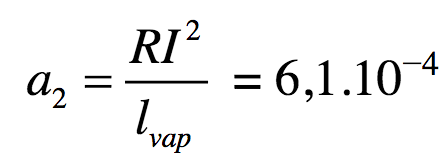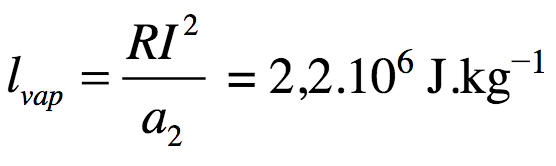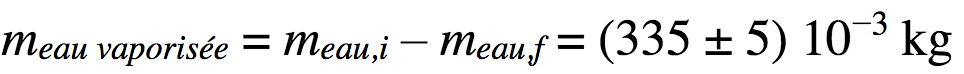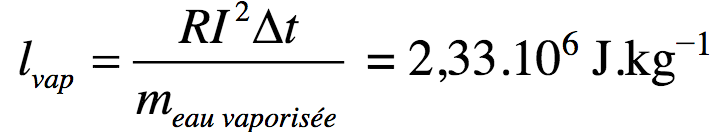Détermination expérimentale de la capacité thermique massique et de l'enthalpie massique de vaporisation de l'eau

De l’énergie thermique apportée à l’eau permet d’augmenter sa température ou d’effectuer la transition de phase liquide-vapeur (vaporisation). On se propose dans cet article de retrouver expérimentalement la capacité thermique massique et la chaleur latente massique de vaporisation (ou enthalpie massique de vaporisation) de l’eau pour mieux comprendre leurs effets.

On place une masse $m_{\mathrm{eau}}$ = 1,00 kg d’eau dans une bouilloire et on mesure à la fois la température de l’eau et la masse de l’ensemble au cours du temps, figure 1. la bouilloire reste ouverte tout au long de la manipulation. Un ventilateur permet en outre d'évacuer plus facilement la vapeur d'eau afin d'éviter que celle-ci ne se recondense dans le système. La laine de verre est placée autour de la bouilloire, mais pas au dessus, afin de limiter les pertes thermiques. La bouilloire dispose d’une résistance chauffante R = 40 Ω dissipant de l’énergie thermique par effet Joule. La puissance thermique moyenne dissipée vaut :

En prenant $U$ = 230 V la valeur efficace de la tension du secteur. Attention, on note tout de même que la tension du secteur n'est pas constamment égale à 230 V. Il existe des variations temporaires de ±10% sur la valeur efficace délivrée par le fournisseur d'électricité.

Figure 1.  Bouilloire vue de dessus. On distingue la résistance chauffante et la couche d’isolation thermique

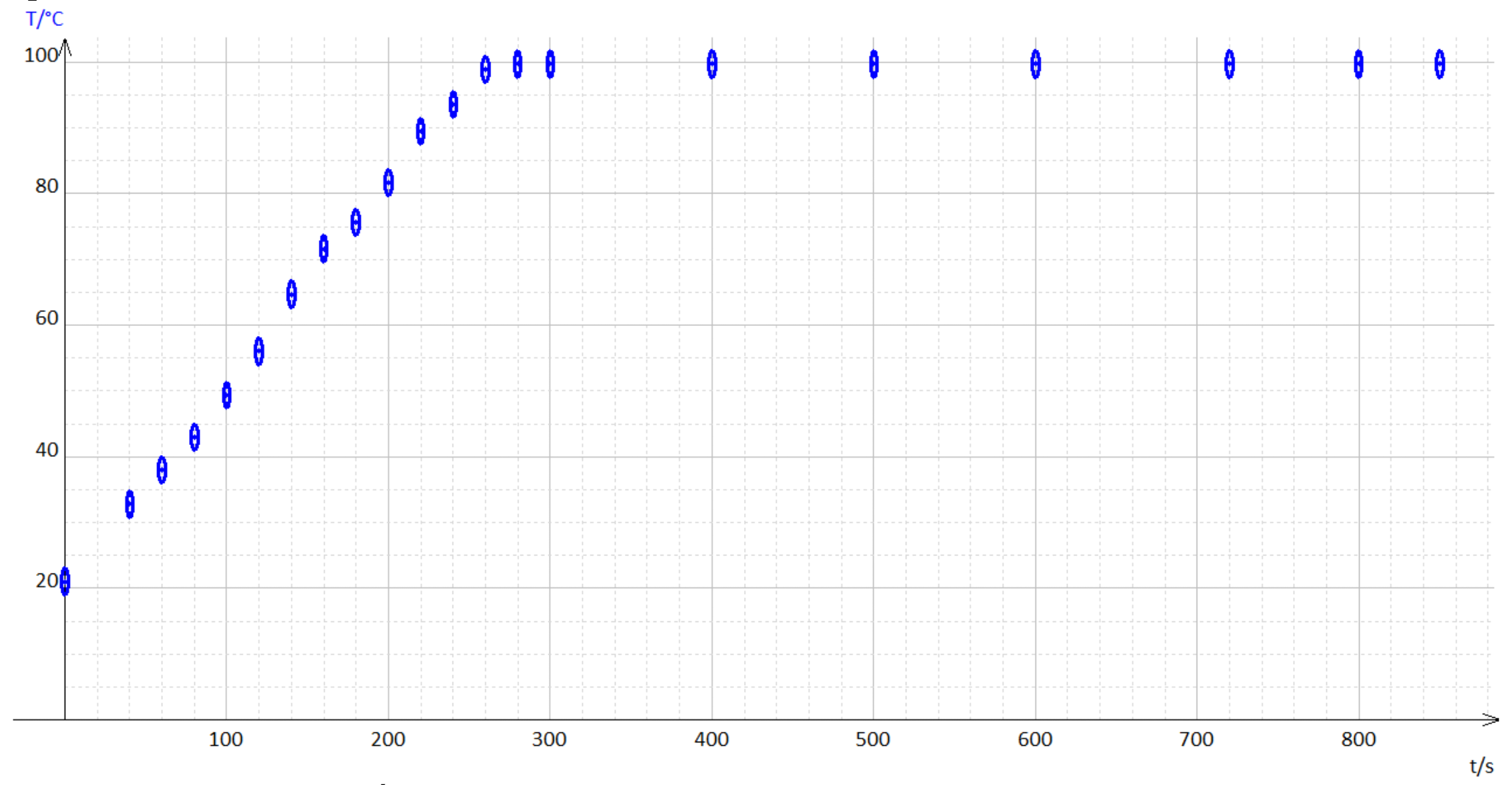
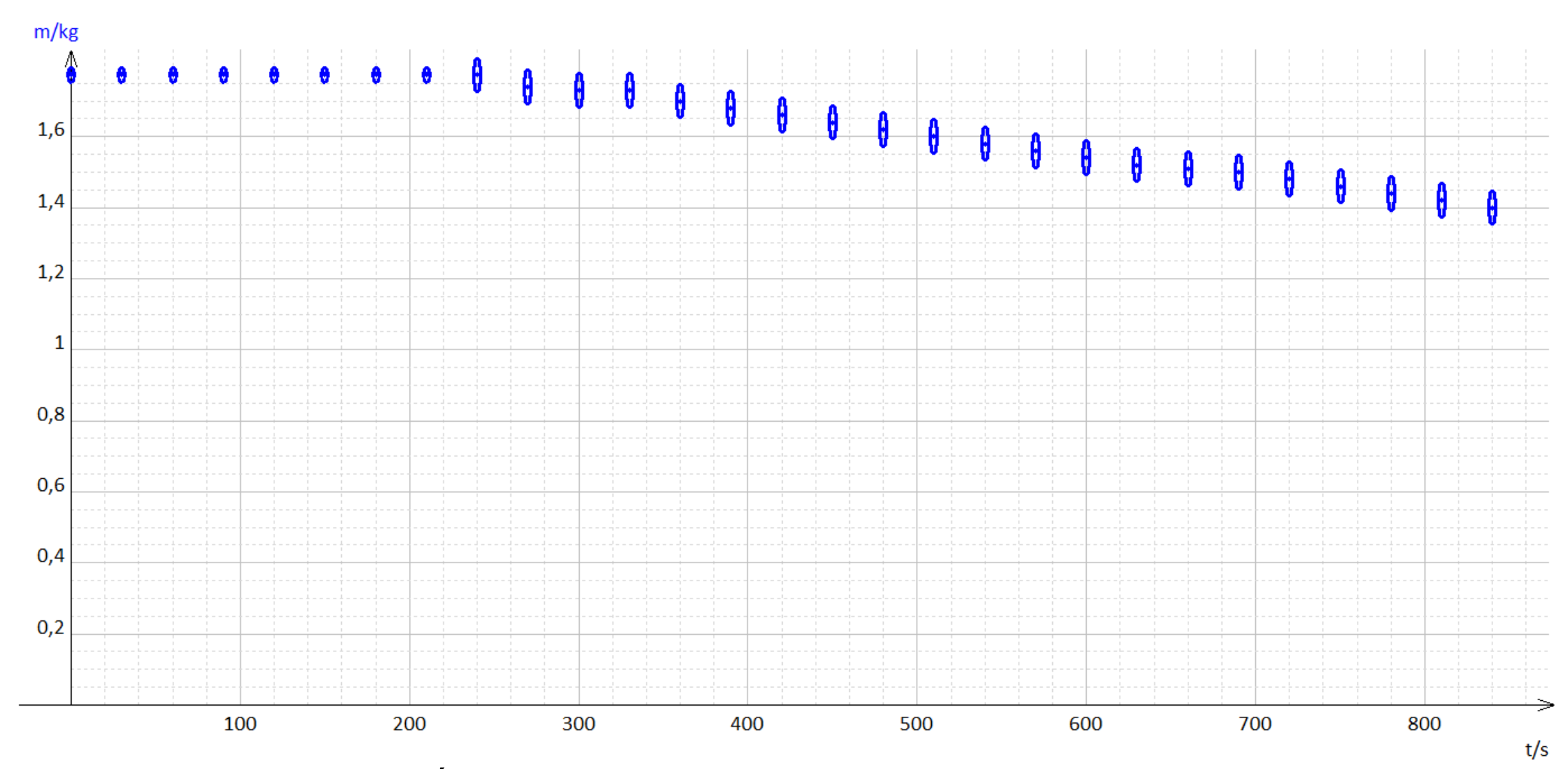
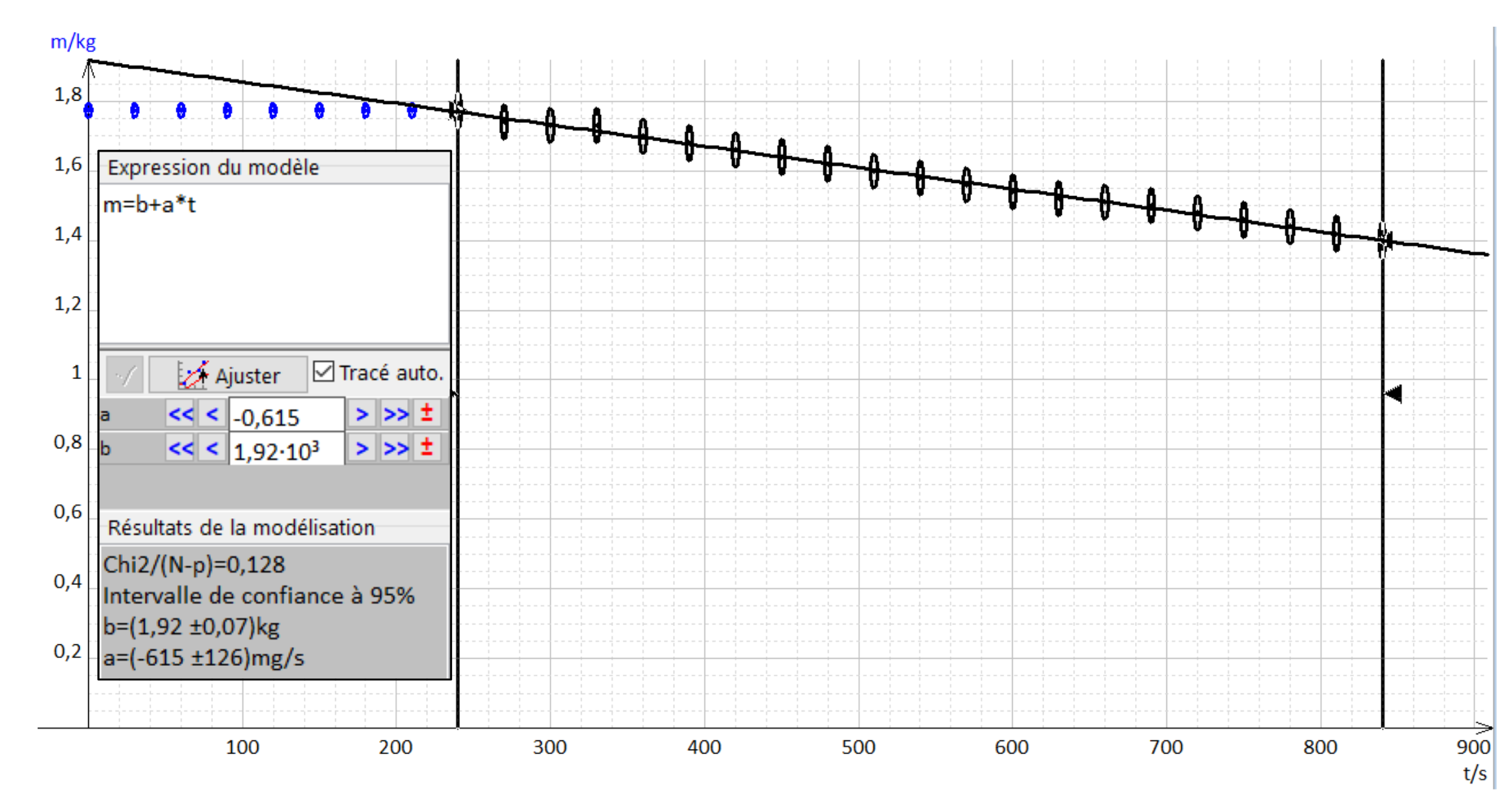
La température de l’eau augmente rapidement au cours du temps. Il faut bien mélanger l’eau dans la bouilloire pour homogénéiser la température. Pendant ce temps, la masse d’eau dans la bouilloire reste constante. À partir de 240 s, l’eau se met à bouillir. La température se stabilise alors au voisinage de 100°C, tandis que la masse d’eau dans la bouilloire diminue. Les remous dus à l’ébullition de l’eau font trembler la bouilloire sur la balance, ce qui rend plus difficile la mesure de la masse et tend à augmenter les incertitudes. Lors de l'expérience, il est alors nécessaire de scotcher soigneusement le fil d'alimentation.

On utilise un ventilateur qui permet d’évacuer la vapeur d’eau produite et éviter qu’elle ne se condense dans la bouilloire.

Finalement, ici, la bouilloire fait office de calorimètre bon marché.

Les évolutions de la température et de la masse de l’eau au cours du temps sont présentées sur les figures 2 et 3.

Figure 2.  Évolution de la température de l’eau au cours du temps. La température augmente jusque 100°C puis reste constante durant l’ébullition

Figure 3.  Évolution de la masse de l’eau au cours du temps. La masse reste d’abord constante pendant la phase de chauffe, puis diminue au cours de l’ébullition

On suppose que les pertes thermiques vers l’extérieur peuvent être négligées. Durant la phase de chauffe, l’énergie thermique apportée par la résistance chauffante permet d’augmenter la température de l’eau. La conservation de l’énergie permet d’écrire :

où $c_{\mathrm{eau}}$ est la capacité thermique massique de l’eau. Dans ce modèle, la température de l’eau évolue de façon affine avec le temps :

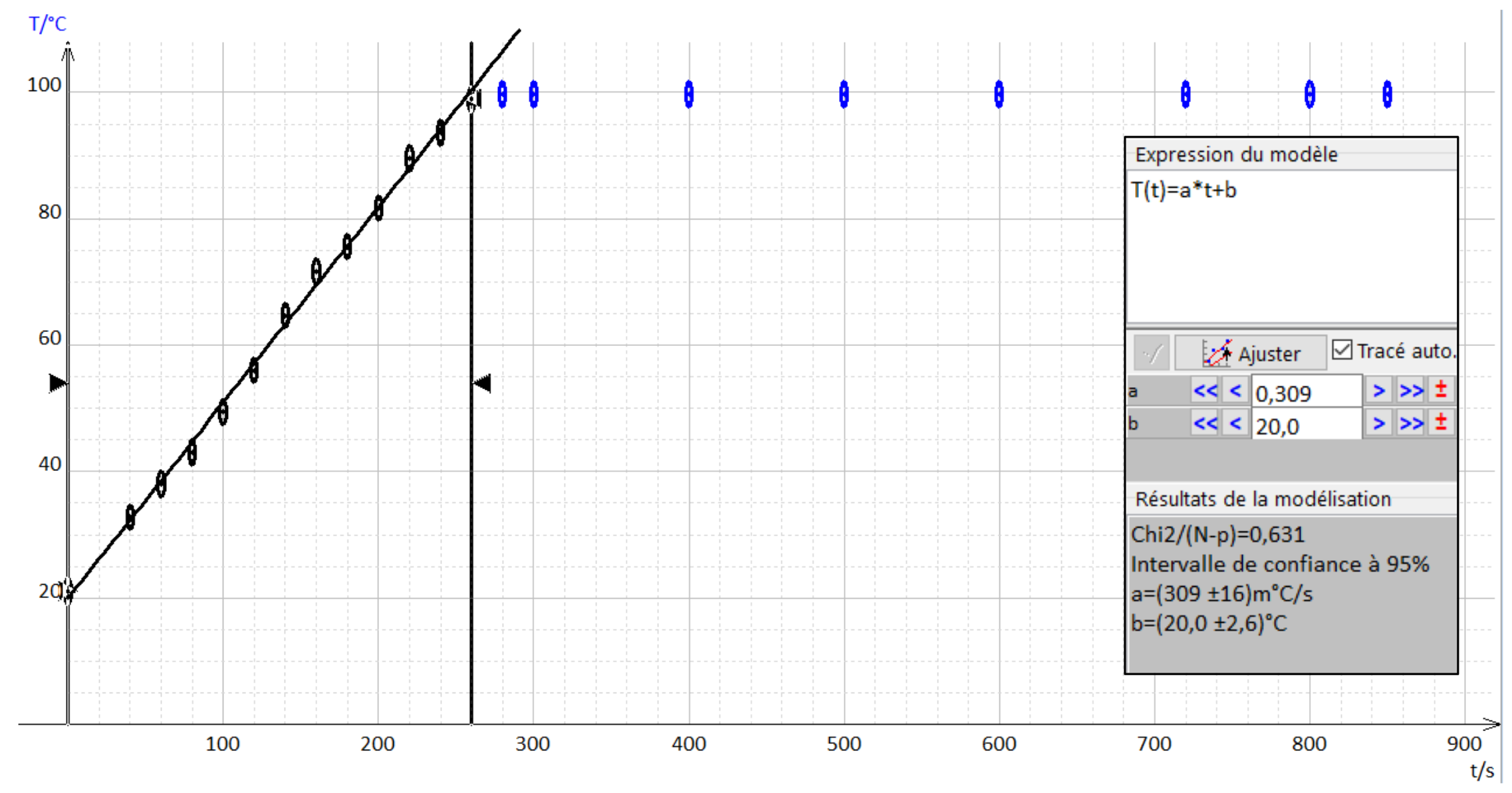
Ce résultat est bien en accord avec les points expérimentaux, figure 4.

Figure 4.  Présentation des différentes situations

Une régression linéaire pendant la phase de chauffe permet d’obtenir :

avec l’incertitude ${\mathrm{\Delta a}}_1$ = 0,02 K.s^-1

On en déduit :

avec l’incertitude relative : $\genfrac{}{}{0.1ex}{}{{\mathrm{\Delta c}}_{\mathrm{eau}}}{c_{\mathrm{eau}}}=\genfrac{}{}{0.1ex}{}{{\mathrm{\Delta a}}_1}{a_1}$ = 6,5%

On retrouve bien, aux incertitudes près, la valeur tabulée $c_{\mathrm{eau}}$ = 4,18.10³ J.kg^-1K^-1

Durant la phase d’ébullition, l’énergie thermique apportée permet la vaporisation de l’eau sous la pression atmosphérique constante. La conservation de l’énergie s’écrit dans ce cas :

où $l_{\mathrm{vap}}$ est l’enthalpie massique de vaporisation de l’eau et t₀ l’instant de début de l’ébullition. La masse d’eau vaporisée s’écrit en fonction de la masse d’eau initiale et de la masse d’eau restante :

Dans ce modèle, la masse d’eau dans la bouilloire varie de façon affine avec le temps :

Ce résultat est à nouveau en accord avec les mesures expérimentales, figure 5.

Figure 5.  Modélisation de la diminution de la masse d'eau durant l'ébullition

Une régression linéaire pendant l’ébullition permet d’obtenir :

avec l’incertitude ${\mathrm{\Delta a}}_2$ = 1,3.10^-4 kg.s^-1

On en déduit :

avec l’incertitude relative : $\genfrac{}{}{0.1ex}{}{{\mathrm{\Delta l}}_{\mathrm{vap}}}{l_{\mathrm{vap}}}=\genfrac{}{}{0.1ex}{}{{\mathrm{\Delta a}}_2}{a_2}$ = 21%

La valeur tabulée de l'enthalpie massique de vaporisation vaut $l_{\mathrm{vap}}$ = 2,1.10⁶ J.kg^-1.

On retrouve expérimentalement la valeur tabulée aux incertitudes de mesure près. Celles-ci sont particulièrement importantes pour cette expérience à cause de la mesure de la masse à la balance au cours de l’ébullition.

Après $\mathrm{\Delta t}$ = 600 s d’ébullition, on a arrêté la bouilloire et laissé l’eau se refroidir. On a alors mesuré la masse d’eau restante : $m_{\mathrm{eau,f}}$ = 665 ± 5.10^-3kg.

La masse d’eau vaporisée pendant cette durée vaut donc :

On en déduit une autre mesure de l’enthalpie de vaporisation de l’eau

avec l’incertitude relative : $\genfrac{}{}{0.1ex}{}{{\mathrm{\Delta l}}_{\mathrm{vap}}}{l_{\mathrm{vap}}}=\genfrac{}{}{0.1ex}{}{{\mathrm{\Delta m}}_{\mathrm{eau\; vap}}}{m_{\mathrm{eau\; vap}}}$ = 1,5%