Illustration expérimentale de la propagation de solitons le long d'une chaîne de pendules couplés

Un soliton est une onde de grande amplitude et de relativement faible extension spatiale capable de se propager sur de longues distances sans déformation.

Les solitons sont devenus indispensables pour décrire des phénomènes tels que la propagation de certaines ondes en hydrodynamique, les ondes localisées dans les plasmas astrophysiques, la propagation de signaux dans les fibres optiques, ou des aspects beaucoup plus microscopiques comme les phénomènes de transport de charge dans les polymères conducteurs, les modes localisés dans des cristaux magnétiques, la dynamique de macromolécules biologiques comme l'ADN et les protéines par exemple. Bien entendu tous ces systèmes ne sont décrits qu'approximativement par les équations de la théorie des solitons. On parle alors de quasi-solitons. Mais la caractéristique remarquable des solitons est qu'ils sont exceptionnellement stables vis-à-vis des perturbations. Ils sont en outre capables de se former spontanément dans un système physique auquel on fournit de l'énergie, par exemple sous forme thermique, par une onde électromagnétique ou une action mécanique, même si l'excitation initiale ne correspond pas exactement à un soliton. C'est cette propriété qui fait tout l'intérêt des solitons en physique car, si un système possède des caractéristiques permettant l'existence de solitons, et c'est le cas pour beaucoup d'entre eux, il existe alors une très forte chance qu'une excitation intense conduise à leur formation.

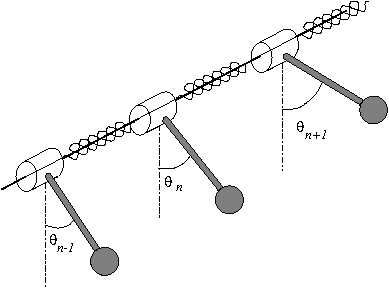
On réalise une chaîne de pendules simples couplés par des ressorts de torsion, schématisée sur la figure 1.

Thierry Dauxois

Figure 1. Éléments de la chaîne de pendules couplés par des ressorts de torsion

Les pendules sont mobiles autour d'un axe commun et deux pendules consécutifs sont reliés par un ressort de torsion. L'énergie du système est la somme, sur toutes les mailles de la chaîne, de trois contributions :

L'énergie initiale du système est injectée lors de l'excitation, réalisée en soulevant plus ou moins quelques pendules à une extrémité de la chaîne. On a filmé la propagation d'ondes le long de cette chaîne, différentes selon le type d'excitation.

Pour une faible excitation, c'est-à-dire un faible déplacement des pendules à un bout de la chaîne, les angles de torsion θ des pendules restent petits. On observe une onde progressive classique (du type phonon), solution d'une équation différentielle linéaire grâce à l'approximation sin θ ≃ θ (Voir « Les différentes équations du mouvement et leurs solutions » en fin d'article).

Cette vidéo permet de voir la propagation de ces ondes linéaires le long de la chaîne. A un instant donné, pratiquement tous les pendules de la chaîne sont en mouvement : l'onde est délocalisée. Arrivées au bout de la chaîne, ces ondes se réfléchissent, puis reviennent vers l'extrémité où elles ont été crées.

Cette vidéo propose unzoom sur le mouvement des pendules lorsqu'une onde linéaire se propage.

Pour une excitation forte - en imposant une rotation de plus d'un demi-tour aux premiers pendules - on observe le retournement successif des pendules suivants. La zone de retournement se propage sans déformation à vitesse constante : c'est un exemple de soliton. La perturbation ne concerne qu'une vingtaine de pendules à la fois, elle est donc localisée dans l'espace. L'équation différentielle correspondante est non linéaire, à cause du terme en sin θ (équation de sine-Gordon, lire en fin d'article la partie « Les différentes équations du mouvement et leurs solutions »).

Cette vidéo montre comment on crée une excitation de type soliton en faisant faire brutalement un tour complet aux pendules situés à l'extrémité droite de la chaîne. Un soliton se propage alors sans que l'on puisse noter de modification de sa forme ni de sa vitesse.

Photographie de la chaîne de pendules qui permet de montrer le passage des pendules à la verticale. Cette perturbation interpole donc deux états différents. À gauche, les pendules font un angle nul par rapport à la verticale, alors qu'à droite ils font un angle de 2π. Les pendules au centre, situés au niveau de la perturbation, correspondent à des valeurs de θ intermédiaires entre 0 et 2π.

Figure 5. La chaîne de pendules lors du passage d'un soliton

Origine du mot « soliton » :

Quelques propriétés remarquables de ces solitons :

Les solitons de SG peuvent exister au repos contrairement aux solitons hydrodynamiques. Le début de cette vidéo montre qu'on peut effectivement avoir une excitation fortement non linéaire et bien statique.

Les solitons ayant certaines caractéristiques de particules, on peut avoir l'idée de créer des collisions entre ces quasi-particules. Ces solitons ont la propriété remarquable de se croiser sans se voir ou presque.

Cette vidéo montre la collision d'un soliton statique, placé au milieu de la chaîne, avec un soliton mobile que l'on crée au niveau de l'extrémité droite de la chaîne. Après la collision, on retrouve le soliton statique au centre, non perturbé, alors que le soliton mobile, qui l'a traversé de façon transparente, continue sa course vers la gauche.

Il existe en réalité deux types de solution à l'équation de sine-Gordon : les solutions « soliton » et « antisoliton », représentées sur la figure suivante. Leur passage fait faire un tour complet aux pendules ; le passage d'un soliton les laisse avec un angle θ valant 2π tandis que celui d'un antisoliton les fait revenir à un angle θ nul. Comme elles sont associées à des variations rapides d'une grandeur - ici l'angle de torsion θ -, elles sont souvent désignées par le terme anglais « kink » (ou « antikink » pour l'antisoliton).

Thierry Dauxois

Figure 8. Solutions soliton (a) et antisoliton (b) de la chaîne de pendules

Dans un milieu infini comportant un seul soliton, on peut changer sa vitesse par des perturbations, ou même le stopper complètement, mais pas le faire disparaître. Les pendules n'étant pas dans le même état des deux côtés du soliton, on parle de soliton « topologique », par opposition aux solitons hydrodynamiques qui sont qualifiés de « non topologiques ».

Les solutions phonons (ondes linéaires), et solitons (ainsi que les antisolitons bien sûr) constituent l'ensemble des solutions du modèle sine-Gordon sur lesquelles on peut par conséquent décomposer tout état du système. Une méthode, que l'on appelle méthode de diffusion inverse, montre que ces solutions variées constituent en quelque sorte les « modes normaux » non linéaires du système puisque un état quelconque du système apparaît comme une combinaison de ces « modes ».

Pour aller plus loin, des livres et des sites internet :

En notant θ_n l'écart angulaire du pendule n par rapport à sa position d'équilibre, I le moment d'inertie d'un pendule par rapport à l'axe, C la constante de raideur des ressorts de torsion, ℓ la distance à l'axe de son centre de gravité, m sa masse et g l'accélération de la pesanteur, l'énergie du système s'écrit :

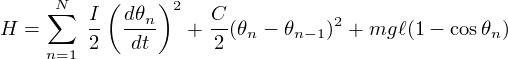
qui permet d'obtenir les équations du mouvement de la chaîne de pendules :

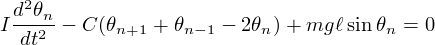
On ne connaît pas la solution exacte de ces N équations différentielles ordinaires. On peut cependant obtenir une solution approchée de cette équation grâce à l'approximation des milieux continus qui sera valable si le couplage entre les pendules est suffisamment fort pour que la variable θ varie peu d'un pendule à l'autre. Notons a la distance entre les pendules et remplaçons les variables discrètes θ_n par la fonction θ(x,t) où θ_n=θ(x=na,t). Le développement de Taylor de θ_n±1 conduit à :

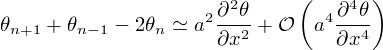
en tenant compte de la décroissance rapide des termes successifs qui contiennent les dérivées d'ordre croissant d'une fonction qui varie lentement avec l'espace. Nous nous limiterons ici au développement à l'ordre le plus bas, c'est-à-dire à son premier terme non nul.

En introduisant les deux quantités suivantes, 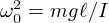et 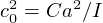, homogènes respectivement au carré d'une pulsation et d'une vitesse, on aboutit finalement à l'équation aux dérivées partielles :

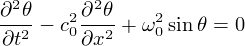
qui est connue sous le nom d'équation de sine-Gordon (ou plus brièvement "SG").

La chaîne de pendules n'est bien sûr qu'une réalisation approximative de l'équation SG puisqu'elle n'est pas décrite exactement par l'équation continue (les effets de la discrétisation n'étant pas totalement négligeables) mais surtout parce qu'elle est faiblement dissipative en raison des frottements au niveau de l'axe de rotation des pendules. Elle constitue néanmoins un modèle intéressant qui permet d'observer les propriétés remarquables des solitons.

Si l'on ne se restreint pas à des petits mouvements d'oscillations des pendules, on peut alors obtenir des solutions non linéaires et localisées spatialement dans le cas 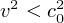. Ces solutions, qui se déplacent avec un profil constant, mobiles à la vitesse v, sont appelées solitons et ont pour expression

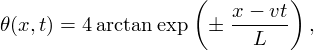
dans laquelle

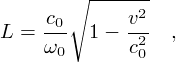
mesure l'extension spatiale de la solution.

La solution permet de retrouver une forme caractéristique liée à l'invariance de Lorentz relative à la vitesse c₀. La contraction de Lorentz du soliton correspond à la racine dans l'expression de L : la largeur du soliton tend vers 0 lorsque sa vitesse v tend vers la vitesse du son c₀. Cette contraction de Lorentz est visible sur l'expérience de la chaîne de pendules quand on compare la largeur d'un soliton statique à celle d'un soliton que l'on a lancé à vitesse élevée. La chaîne de pendules permet par conséquent de faire une « expérience de relativité » où c₀ joue le rôle de vitesse limite.

L'énergie de la solution

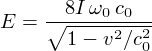
prend également la forme d'une expression « relativiste », vis-à-vis de la vitesse c₀, pour l'énergie d'une particule de masse 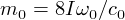. Le soliton de SG possède donc les propriétés d'une quasi-particule relativiste.