Activer le mode zen
Ressource au format PDF
Classification
L'horaire des marées et la masse de la Lune
02/07/2013
Résumé
Détermination du rapport masse de la Lune / masse de la Terre par la mesure du décalage horaire des marées aux syzygies et aux quadratures.
Table des matières
En 1687, Newton[1] effectue la première estimation du rapport masse de la Lune / masse de la Terre à 1/39,8 (aujourd'hui 1/81). Sa méthode est la suivante : 1) il utilise les variations mensuelles de la hauteur des marées dans le port de Bristol pour quantifier le rapport des marées lunaires sur les marées solaires à 4,48 (aujourd'hui 2,1) ; 2) ce rapport lui permet de calculer le rapport masse de la Lune / masse du Soleil ; 3) connaissant le rapport masse du Soleil / masse de la Terre, il peut calculer le rapport cherché (cf. Comment déterminer la masse de la Lune à partir des marées sur CultureSciences Physique.
En 1740, Daniel Bernoulli[2] reprend le même procédé mais il change la première détermination : il quantifie le rapport des marées lunaires sur les marées solaires non plus en utilisant la hauteur des marées mais leurs horaires. Il trouve un rapport de 2,5 ce qui lui permet de ramener le rapport masse de la Lune / masse de la Terre à 1/70. Dans cet article, nous exposons sa méthode pour trouver le rapport des forces de marées en nous appuyant sur la présentation très claire qu'en fait la marquise du Châtelet[3] dans ses commentaires aux Principes Mathématiques de la Philosophie Naturelle de Newton de 1756.
Figure 1. Les quatre personnages-clés de cette histoire
Newton (1643 – 1727), scientifique anglais assez universel mais surtout connu pour ses travaux en physique et mathématique. Son œuvre majeure Philosophiae Naturalis Principia Mathématica a été publiée en 1687.
Émilie du Chalelet (1706-1749), sans doute la première femme scientifique française (physique et mathématique). Elle est surtout connue pour avoir traduit (du latin au français) et commenté les œuvres de Newton et pour avoir été la maîtresse de Voltaire.
Daniel Bernouilli (1700-1782), mathématicien et physicien suisse, un des 3 membres célèbres de cette famille de scientifiques suisses avec son père Jean (1667-1748) et son oncle Jacques (1654-1705).
Pierre-Simon de Laplace (1749-1827), mathématicien, astronome et physicien français, un des plus grand scientifiques français du 19ème siècle, également connu pour ses rapports et dialogues avec Napoléon dont le très célèbre. Napoléon : « Monsieur de Laplace, je ne trouve pas dans votre système mention de Dieu ? », Laplace : « Sire, je n'ai pas eu besoin de cette hypothèse. […] Cette hypothèse [Dieu], Sire, explique en effet tout, mais ne permet de prédire rien. En tant que savant, je me dois de vous fournir des travaux permettant des prédictions ».
Une première approche qualitative
La période synodique de la Lune (intervalle entre deux Pleines Lunes consécutives) est de 29,53 jours. C'est le temps que met la Lune pour tourner de 360° par rapport à la ligne Terre-Soleil. Chaque jour, la Lune prend donc un peu de retard par rapport au Soleil. Elle se décale en moyenne chaque jour d'un angle égal à 360°/29,53 = 12,2°, ce qui fait qu'elle repasse au méridien du lieu environ 49 minutes après le Soleil ( (12,2×24h×60)/360 = 49min) le lendemain de la nouvelle Lune, 98 minutes (=1h36) le surlendemain... Ce décalage quotidien induit que les marées hautes se produisent toutes les 12h24 et non pas toutes les 12h. D'une journée à l'autre, la marée haute "du matin" (ou "du soir") retarde donc de 49 minutes par rapport à la mérée équivalente de la veille. Mais il ne s'agit que d'une valeur moyenne car dans les syzygies (Pleine et Nouvelle Lune), lorsque les actions de la Lune et du Soleil se conjuguent, la durée est plus courte (24h35min selon Bernoulli) et dans les quadratures (Premier et Dernier Quartier), lorsque les actions de la Lune et du Soleil se retranchent, elle est plus longue (25h25min toujours selon Bernoulli). Ces variations dans le retour des marées hautes proviennent des combinaisons multiples entre les marées lunaires et les marées solaires. Elles permettent de déterminer le rapport des marées lunaires sur les marées solaires.
Notre étude n'est possible que grâce à des hypothèses très simplificatrices : 1) l'orbite de la Lune et l'orbite apparente du Soleil sont supposées dans le plan de l'équateur ; 2) l'intervalle de temps entre deux marées hautes d'une journée sur l'autre est calculé uniquement pour des points de l'équateur terrestre ; 3) les effets dynamiques dus à la rotation terrestre (forces de Coriolis) et à la résonance des bassins océaniques ne sont pas pris en compte (hypothèse des marées d'équilibre).
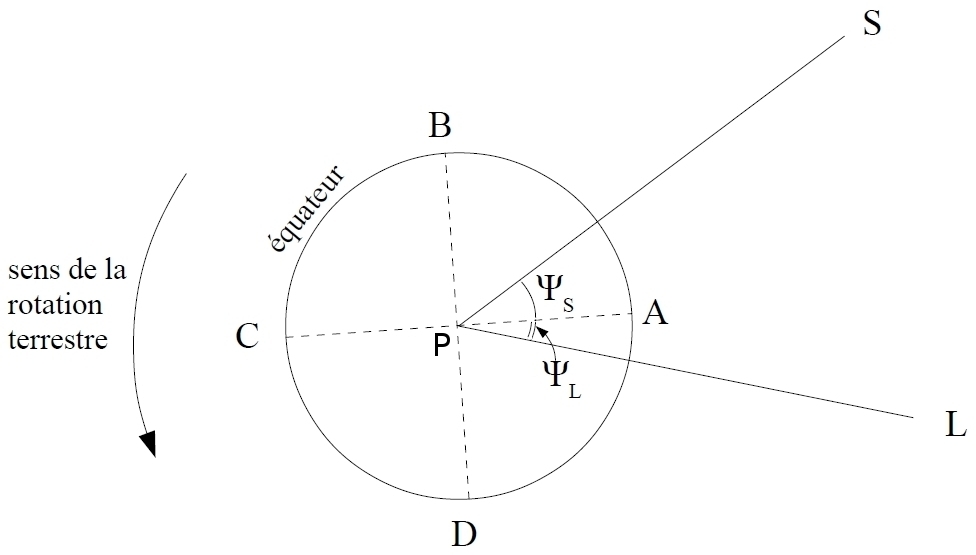
Figure 2. Schéma de principe des positions relatives Terre-Lune-Soleil pour l'étude des marées océaniques
Le schéma est dans le plan de l'équateur. Le point central est un pôle (P). ABCD est la surface de l'océan qui recouvre toute la Terre. Chaque astre (le Soleil, S, et la Lune, L) déforme la surface des eaux en un ellipsoïde dont le grand axe est dirigé vers lui (les déformations de l'océan ne sont pas représentées sur le schéma). La combinaison des deux ellipsoïdes génère une marée haute en A et en C et une marée basse en B et D. La Lune est repérée par rapport au point A par l'angle ΨL et le Soleil par l'angle ΨS . L'angle ΨS permet de connaître l'horaire de la marée.
Décalage des horaires de marées lors des syzygies
Lors d'une syzygie, la Terre, la Lune et le Soleil sont alignés (figure ci-dessous). La marée haute survient lors du passage des deux astres au méridien. Le jour suivant, la Lune s'est décalée par rapport au Soleil. La somme des déformations de l'océan dues à la Lune et au Soleil est maximale pour un point situé entre les deux astres. La marée haute advient donc après le passage du Soleil au méridien et avant celui de la Lune. Si les deux astres avait une action similaire, la marée haute se déroulerait exactement au milieu des deux passages, c'est-à-dire 24,5min après le passage du Soleil. Plus la Lune a une action prépondérante, plus la marée va se décaler vers le passage de la Lune.
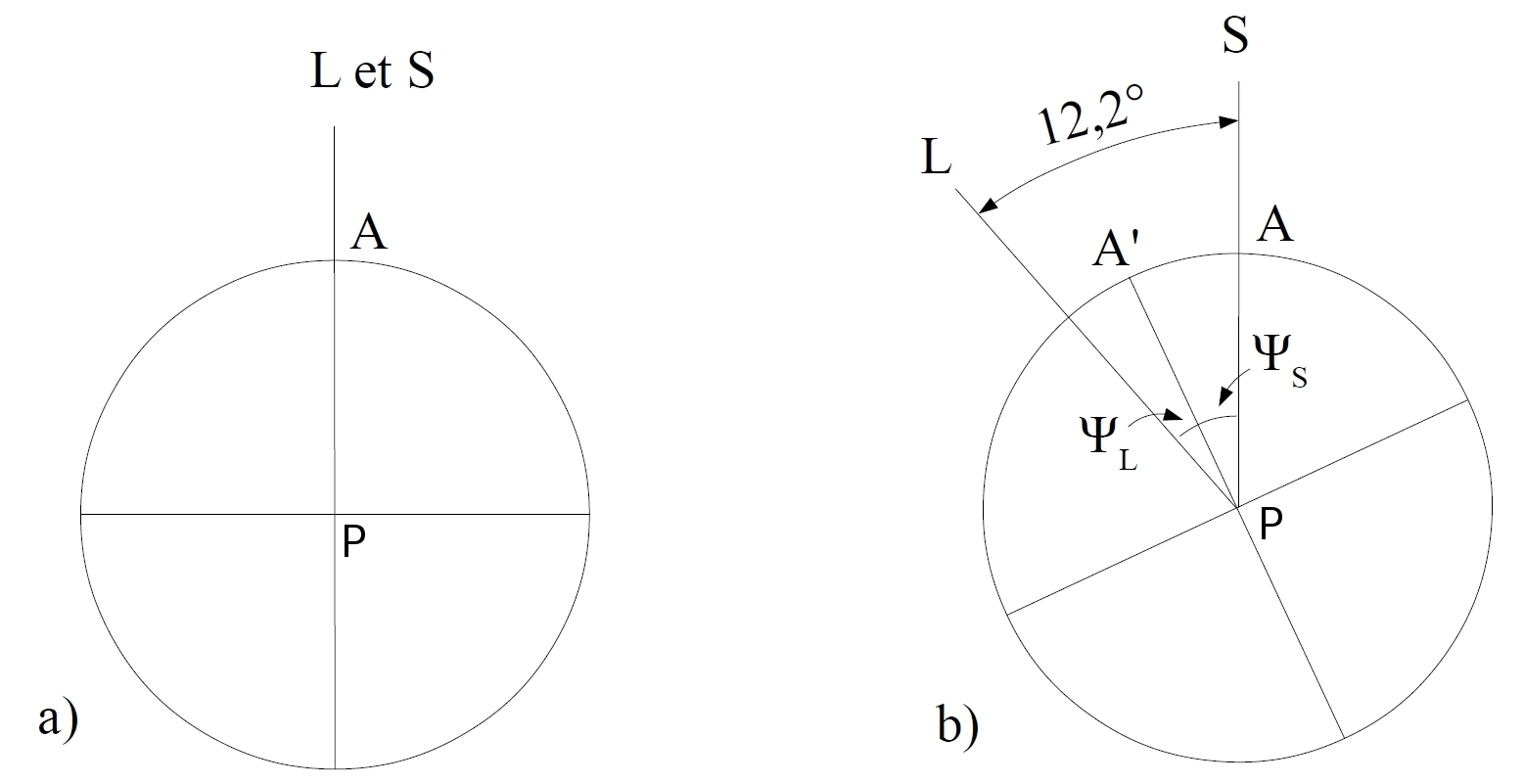
Figure 3. Décalage de l'horaire de marée haute aux syzygies (ici, la Nouvelle Lune)
a) Lors d'une Nouvelle Lune, la Lune et la Soleil sont au zénith d'un point A, où la marée est haute.
b) Le jour suivant la syzygie de Nouvelle Lune, la Lune s'est décalée de 12,2° par rapport au Soleil. Lorsque le Soleil repasse au méridien du lieu A (soit exactement 24h plus tard), la marée haute a lieu en A'. Le point A doit donc encore tourner de l'angle ΨS pour connaître la marée haute. L'angle ΨS, exprimé en minutes de temps, donne le décalage temporel de la marée haute d'une journée à l'autre.
Décalage des horaires de marées lors des quadratures
Lors d'une quadrature, les directions Terre-Lune et Terre-Soleil forment un angle droit. La marée haute a lieu lors du passage au méridien de la Lune puisque c'est elle qui a l'action prépondérante. Le jour suivant, la Lune se rapproche de l'axe Terre-Soleil. La somme des déformations de l'océan dues à la Lune et au Soleil est maximale pour un point situé entre les deux astres. La marée haute survient donc après le passage de la Lune au méridien. L'intervalle des marées hautes d'une journée à l'autre est supérieur à 24h49min.
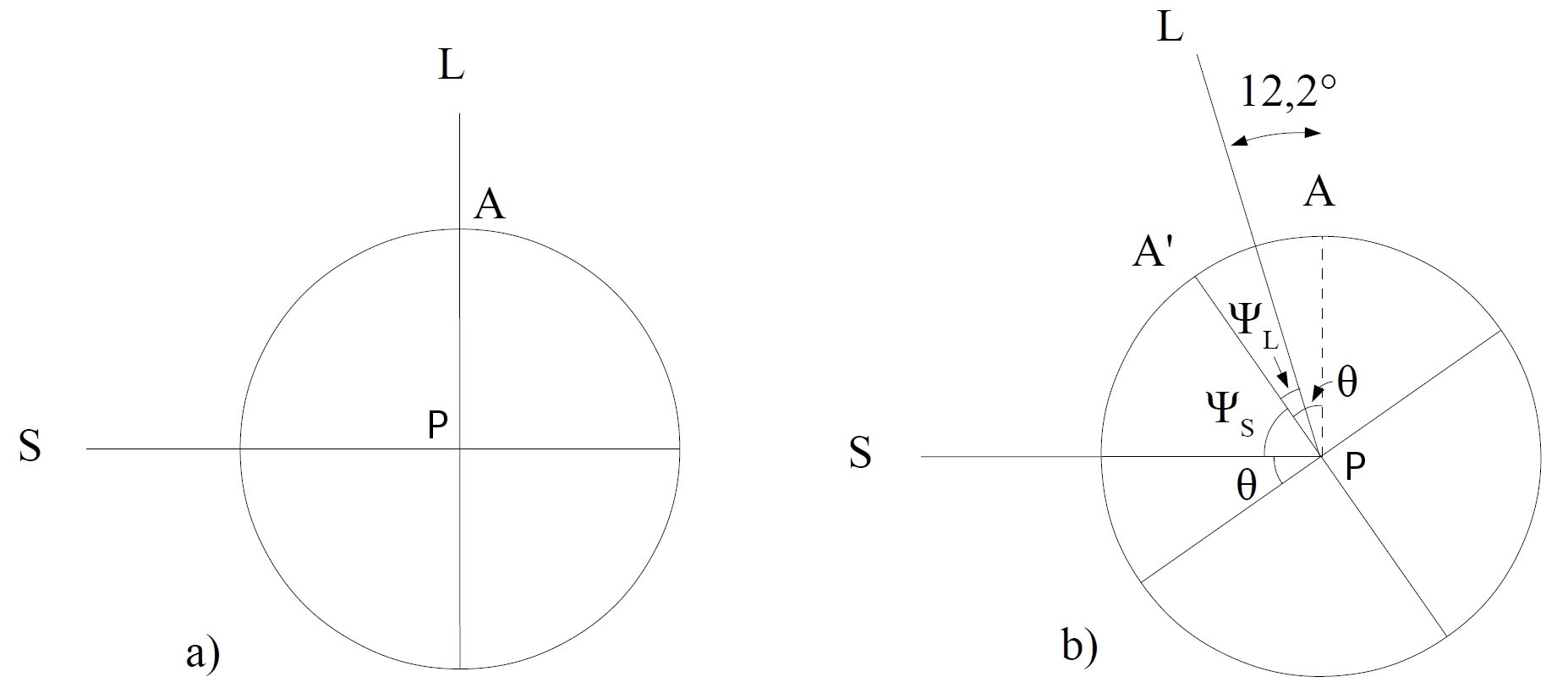
Figure 4. Décalage de l'horaire de marée haute aux quadratures (ici, le Dernier Quartier)
a) Lors d'une quadrature, la Lune est au zénith d'un point A lorsque le Soleil est dans l'horizon. La marée haute a lieu en A.
b) Le jour suivant la quadrature, la Lune s'est décalée de 12,2°. Lorsque le Soleil est à nouveau dans l'horizon du point A (soit exactement 24h plus tard), la marée haute à lieu en A'. Le point A doit donc encore tourner de l'angle θ = 90° - ΨS pour connaître la marée haute.
Approche quantitative
Expression donnant l'élévation des eaux sous l'action combinée de la Lune et du Soleil
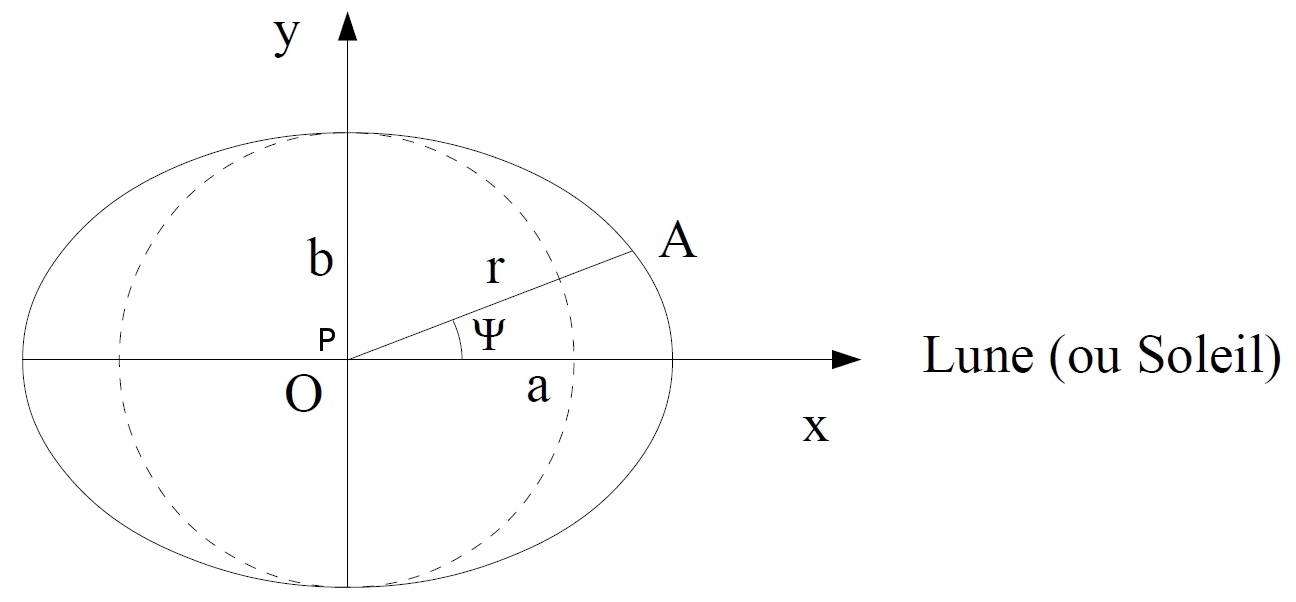
Sous l'action d'un astre seul (Lune ou Soleil), la surface de l'océan se déforme en un ellipsoïde (c'est l'hypothèse des marées d'équilibre). Dans le plan équatorial (sur lequel circulent les astres), la surface est donc une ellipse (cf. figure ci-dessus), de demi-grand axe a et de demi-petit axe b et d'équation cartésienne x2/a2+ y2/b2= 1. Le grand axe de l'ellipse est orienté vers l'astre perturbateur.
L'ellipse peut être paramétrée par : x = a.cosΨ et y = b.sin Ψ. En appelant β, la différence entre le demi-grand axe et le demi-petit axe on a : β=a−b et en supposant que cette différence est petite, l'équation de l'ellipse en coordonnées polaires s'écrit alors :
- r = ( x2+ y2)1/2 = (a2.cos2Ψ + b2.sin2Ψ)1/2 = (b2 + (a2 − b2).cos2Ψ)1/2.
Comme (a2 − b2) = (a+b).(a−b) ≈ 2bβ, il vient : r ≈ b (1 + (2β/b).cos2Ψ)1/2.
Soit, en faisant un développement limité : r ≈ b + β.cos2Ψ.
La Lune et le Soleil agissent simultanément. Comme les déformations occasionnées sont petites, on peut supposer que la surface des eaux est donnée par la somme des déformations. Avec ΨL l'angle repérant la Lune, ΨS celui repérant le Soleil (cf figure 1), βL la différence des demi-axes de l'ellipsoïde causé par la Lune et βS celle relative au Soleil, on a :
- r = constante + βL.cos2ΨL + βS.cos2ΨS.
Trouver le lieu et l'horaire de la marée haute revient à chercher le maximum de la fonction précédente, c'est-à-dire à annuler sa dérivée.
Dérivation de l'expression précédente pour en trouver le maximum
Les angles ΨL et ΨS varient au cours du temps en raison de la rotation propre de la Terre sur elle-même mais aussi du déplacement propre des astres sur leur orbite. Puisque le Soleil repasse au méridien du lieu en 24h et la Lune en 24h50min environ, la variation dΨL est un peu plus lente que la variation dΨS :
- |dΨL / dΨS| = 24h/24h50min=0,966.
Lors des syzygies ou des quadratures, la marée haute survient toujours pour un lieu situé entre les directions de la Lune et du Soleil. La variation de ΨL est donc inverse à celle de ΨS (lorsque l'un des angles augmente, l'autre diminue). Les variations angulaires sont donc de signe opposé, on peut donc reprendre le calcul précédent et écrire : dΨL = - 0,966.dΨS.
En dérivant l'expression donnant la surface des eaux, on obtient :
- βL.cosΨL.sinΨL.dΨL + βS.cosΨS.sinΨS.dΨS = 0,
soit, en faisant intervenir dΨL = - 0,966.dΨS :
- βL / βS = (cosΨS.sinΨS) / (0,966.cosΨL.sinΨL).
Application aux syzygies
La marée haute suivant la Nouvelle Lune (cf. figure 2) survient 35 minutes après le passage du Soleil au méridien, on a donc ΨS = 35/(24×60) x 360 = 8,75°. Puisque la Lune a pris 12,2° de retard par rapport au Soleil, on a alors ΨL + ΨS = 12,2°, d'où ΨL = 12,2° − ΨS = 3,45°.
On obtient alors : βL / βS = (cos8,75.sin8,75) / (0,966.cos3,45.sin3,45) ≈ 2,6.
Application aux quadratures
Puisque la marée haute suivant le Dernier Quartier (cf. figure 3) survient 1h25min (85min) après le lever du Soleil (passage dans l'horizon), θ=85/(24×60) × 360 = 21,25°, d'où ΨS = 90° - θ = 68,75°. On a également ΨL + ΨS = 90° - 12,2° = 77,8°, donc ΨL = 77,8° - 68,75° = 9,05°.
On obtient alors : βL / βS = (cos68,75.sin68,75) / (0,966.cos9,05.sin9,05) ≈ 2,3.
Conclusion
Bernoulli suppose que β, la différence entre le demi-grand axe et le demi-petit axe de l'ellipsoïde des marées est proportionnelle à la force de marée. Le rapport βL / βS, qu'il estime en moyenne à 2,5, lui donne donc directement le rapport des marées lunaires sur les marées solaires. En reprenant la méthode de Newton (cf. Comment déterminer la masse de la Lune à partir des marées sur CultureSciences Physique ou sur Planet-Terre), il peut donc en déduire le rapport masse de la Lune / masse du Soleil puis le rapport masse de la Lune / masse de la Terre.
La méthode est simple et élégante. Hélas, elle est très sensible aux valeurs des observations sur les intervalles des marées. En prenant un intervalle de 24h36min lors des syzygies, au lieu de 24h35min, on trouve que βL / βS = 2,9 ! Si la sensibilité est un peu moins grande aux quadratures, elle reste très importante. Or les observations sur l'horaire des marées sont très délicates. Grâce à une analyse des marées dans le port de Brest sur de nombreuses années, Laplace[4] trouve que l'intervalle entre les marées hautes d'une journée à l'autre est en moyenne de 24h39min lors des syzygies et de 25h15min lors des quadratures, ce qui donne pour le rapport βL / βS les valeurs respectives de 4,0 et 2,8. La méthode ne peut donc pas aboutir à un résultat fiable. C'est pourquoi, pour calculer le même rapport des marées lunaires sur les marées solaires, Laplace préfère revenir à un procédé reposant sur l'analyse des hauteurs, comme l'avait fait Newton. Il obtient βL / βS = 2,5, ce qui lui indique que la Lune est 75 fois moins lourde que la Terre[5].
[1] I. Newton, Principes Mathématiques de la Philosophie Naturelle, traduction de la marquise du Châtelet, 1756, réédition Sceaux, Jacques Gabay, 1990, Tome I, Livre III, proposition 37, p. 96-98.
[2] D. Bernoulli, Traité sur le flux et le reflux de la mer, in Pièces qui ont remporté le prix de l'Académie royale des sciences en 1740, Paris, Martin, Coignard et Guérin, Chapitre VI, Article 10, p.113-117.
[3] La marquise du Châtelet, Commentaires des Principes Mathématiques de la Philosophie Naturelle, publiés à la fin de sa traduction des Principes Mathématiques de la Philosophie Naturelle de Newton, réédition Sceaux, Jacques Gabay, 1990, Section V, articles 22 à 27, p.277-285.
[4] P.S. de Laplace, Traité de mécanique céleste, Tome V, Paris, Bachelier, 1825, réédition New York, Chelsea Publishing Compagny, 1969, Livre XIII, Chapitre IV, p.241.
[5] Ibid., p. 229.
Pour citer cet article :
L'horaire des marées et la masse de la Lune, Vincent Deparis, juillet 2013. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/masse-Lune-horaire-maree.xml