Comment déterminer la masse de la Lune à partir des marées

À l'époque de Newton, deux lois de mécanique sont reliées à la masse des corps du système solaire.

La troisième loi de Kepler. Loi découverte par Johannes Kepler en 1619, valable pour n'importe quelle planète mais que nous appliquons ici à la Terre, elle stipule que le carré de la période de révolution est proportionnel au cube de la distance au foyer, le Soleil. Newton établira que ce facteur de proportionnalité est $G.M_S$ (la masse d'une planète étant négligeable devant celle du Soleil). Soit $G$ la constante de la gravitation ; $n$ le mouvement moyen de la Terre sur son orbite (vitesse angulaire) : $n=\mathrm{2\pi }/T$ avec $T$ la période de révolution de la Terre autour du Soleil ; $d_S$ le demi grand axe de l'orbite de la Terre ; $M_S$ la masse du Soleil et $M_T$ la masse de la Terre (négligeable devant la masse du Soleil), on a donc :

La gravité. À la surface de la Terre, la gravité $g$ a été donnée par Newton en 1687. Soit $R$ le rayon de la Terre et en négligeant l'influence de la rotation journalière de la Terre, il vient :

La troisième loi de Kepler donne accès au produit $G.M_S$ et la pesanteur $g$ au produit $G.M_T$. Mais comme la constante gravitationnelle $G$ est inconnue à l'époque de Newton (elle ne sera "indirectement" déterminée par Henry Cavendish qu'en 1798), il n'y a aucun moyen de connaître la valeur absolue de $M_S$ ou de $M_T$, seul le rapport $M_S/M_T$ peut être calculé. À l'époque de Newton, on ne peut donc pas connaître directement la masse des corps mais uniquement leur masse relative à un autre corps.

Pour la Terre et le Soleil, les deux équations précédentes permettent d'écrire :

Avec $R=6371\text{km}$, $g=\mathrm{9,81}{\text{m.s}}^{\text{-2}}$, $n=\mathrm{1,99}.{10}^{-7}{\text{rad.s}}^{\text{-1}}$ ($T=\mathrm{365,25}\text{jours}$) et $d_{\mathrm{S}}=150\text{millions de km}$, on obtient :

Ce raisonnement ne peut pas être refait pour la Lune car on ne peut pas lui appliquer la troisième loi de Kepler puisqu'elle ne possède pas de satellite naturel. Newton contourne le problème en utilisant les marées océaniques.

Portrait de Newton (1642-1727), par Godfrey Kneller (1689)

Newton comprend que les marées résultent à la fois de l'action de la Lune et du Soleil et qu'elles sont une conséquence inévitable de l'attraction universelle des corps. Il explique que les parties de la Terre, situées à des distances différentes d'un astre (la Lune ou le Soleil), subissent des attractions différentes de la part de cet astre et que ce sont ces différences d'attraction qui mettent les mers en mouvement. La force de marée due à un astre (la Lune ou le Soleil) se calcule ainsi par la différence vectorielle entre l'attraction de l'astre en un point donné et l'attraction de l'astre au centre de la Terre.

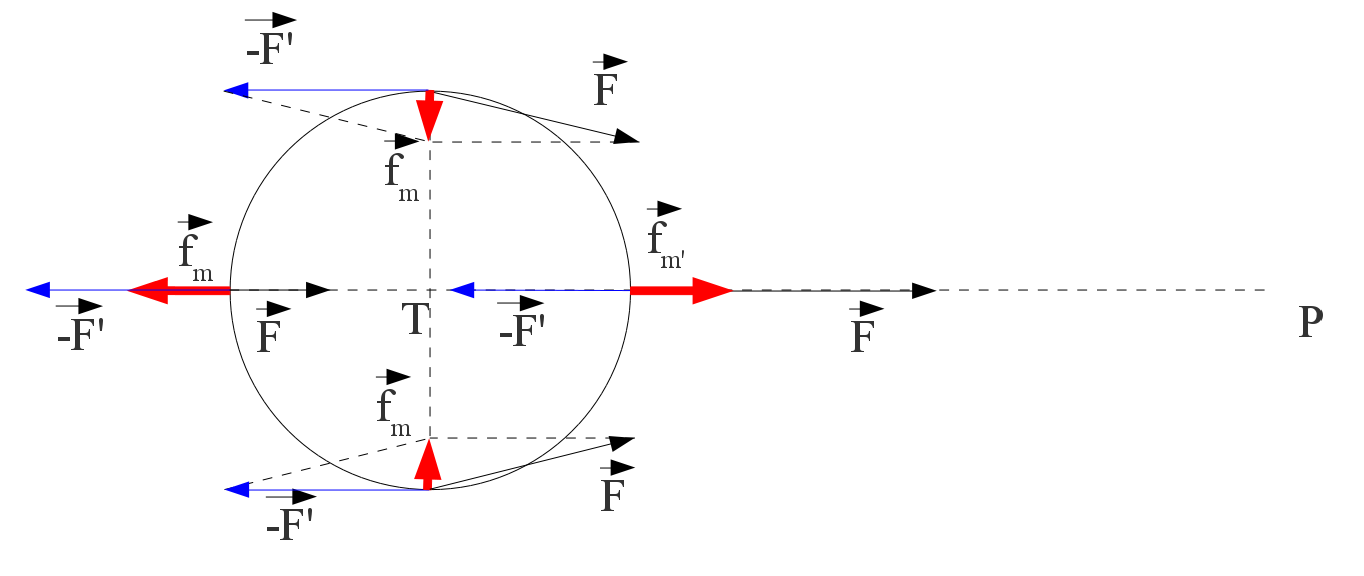
Figure 1. Forces de marée créées par l'astre P (Soleil ou Lune) en différents points de la surface terrestre

Le vecteur force de marée (en rouge) est donné par $\overrightarrow{f_m}=\overrightarrow{F}-\overrightarrow{\mathrm{F\text{'}}}$, avec $\overrightarrow{F}$ l'attraction de l'astre P au point considéré (en noir) et $\overrightarrow{\mathrm{F\text{'}}}$ l'attraction de P au centre T de la Terre (en bleu).

Les particules situées dans l'hémisphère tourné vers l'astre perturbateur sont plus attirées par l'astre que le centre de la Terre : la force de marée pointe vers l'astre. En revanche, les particules qui sont situées dans l'autre hémisphère sont moins attirées que le centre de la Terre : la force de marée est orientée dans le sens opposé. La force de marée s'oppose donc à la pesanteur pour le point situé à l'aplomb de l'astre perturbateur mais également pour le point situé de l'autre côté de la Terre. Elle a des effets identiques dans les deux hémisphères et présente une symétrie presque parfaite. Ceci permet de comprendre pourquoi les marées hautes surviennent au même instant des deux côtés de la Terre.

Newton suppose que la Terre est entièrement recouverte d'un océan. En raison de la symétrie de la force de marée, il affirme que l'océan se déforme en un ellipsoïde allongé, dont le grand axe est constamment dirigé vers l'astre perturbateur. La rotation de la Terre sur elle-même fait qu'un point de la surface terrestre passe successivement par les deux lieux d'élévation maximale et minimale de la mer, ce qui explique les deux marées basses et les deux marées hautes de la journée.

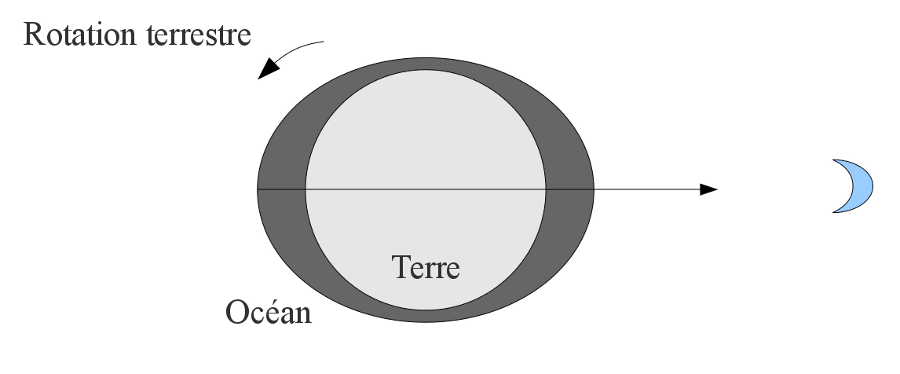
Figure 2. Déformation théorique de l'océan terrestre par les forces de marées

L'océan global, qui entoure la Terre, est déformé en un ellipsoïde par les forces de marée.

Un point de la Terre, entraîné par la rotation journalière, passe par les lieux d'élévation minimale et maximale de l'eau, d'où la succession des deux marées basses et des deux marées hautes au cours d'un journée.

Puisque deux astres agissent (la Lune et le Soleil), l'océan est déformé en deux ellipsoïdes dont les grands axes ont des directions différentes. Les deux ellipsoïdes se mélangent et en fonction de la position relative des astres, ils s'ajoutent (les marées de vives-eaux lors de la Pleine et de la Nouvelle Lune) ou se retranchent (les marées de mortes eaux lors du Premier et du Dernier quartier), ce qui permet à Newton d'expliquer les variations semi-mensuelles des marées.

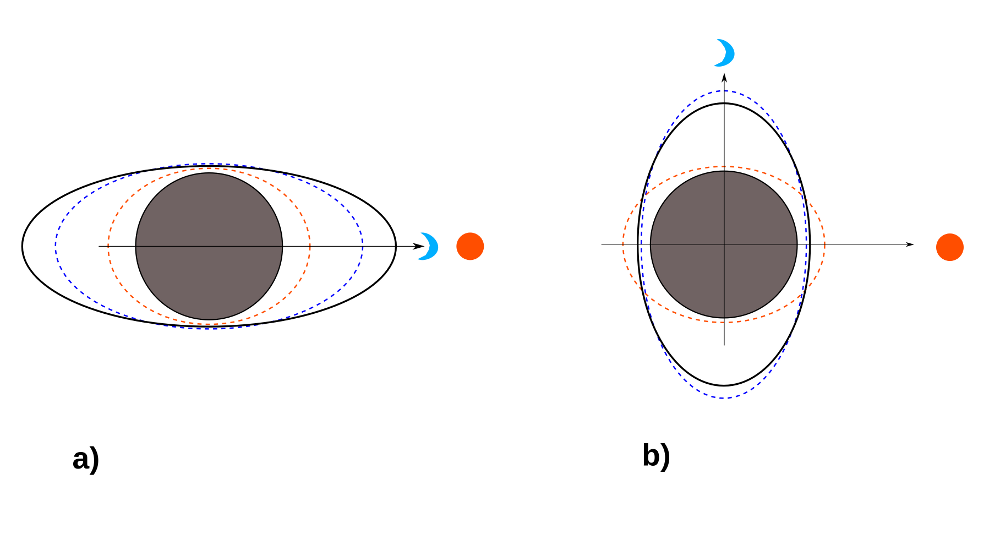
Figure 3. Marées de vives eaux et de mortes eaux

En bleu, la Lune et son "effet de marée" ; en orange, le Soleil et son "effet de marée" ; le trait plein noir indique l'effet de marée cumulé Lune - Soleil.

a) Lorsque la Terre, la Lune et le Soleil sont alignés (pleine ou nouvelle Lune), les marées lunaires et solaires s'ajoutent créant les marées de vives eaux.

b) Lorsque la Terre, la Lune et le Soleil sont en quadrature (premier ou dernier quartier), les marées lunaires et solaires s'opposent mutuellement, créant les marées de mortes eaux.

Newton montre encore que la force de marée exercée par un astre est proportionnelle à la masse de l'astre, au rayon de la Terre et inversement proportionnelle au cube de la distance Terre-astre. Avec nos notations ($M_L$ et $M_S$ les masses de la Lune et du Soleil, $d_L$ et $d_S$ les distances de la Lune et du Soleil à la Terre, et $R$ le rayon de la Terre), on a :

L'idée est de se servir de l'observation des marées pour déterminer le rapport entre les marées lunaires et les marées solaires. Ce rapport permet de connaître le rapport masse de la Lune / masse du Soleil et de là, connaissant le rapport masse du Soleil / masse de la Terre, nous pouvons avoir le rapport masse de la Lune / masse de la Terre. La méthode est basée sur la variation de la hauteur de la marée au cours de la lunaison.

Analyse des observations

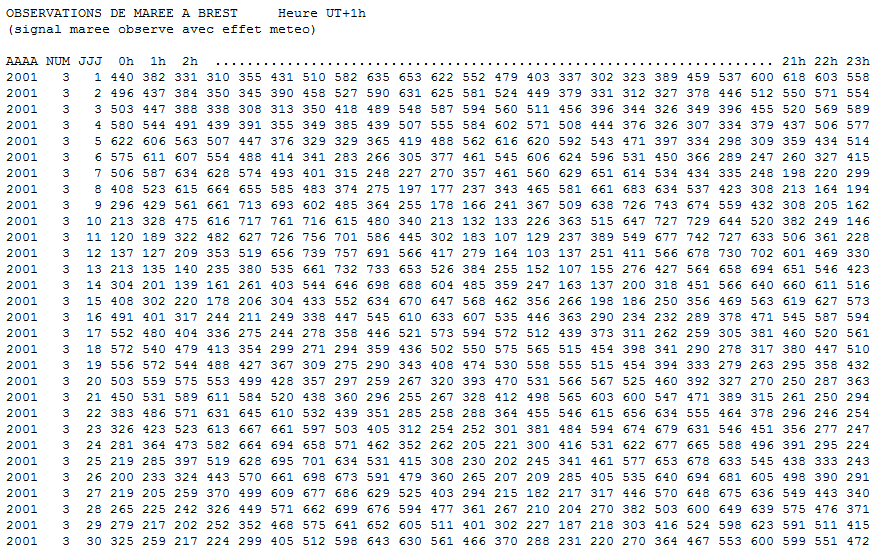
Nous utilisons les données disponibles sur le site internet du SHOM (Service hydrographique et océanographique de la marine : http://www.shom.fr/) pour appliquer la formule précédente. Nous trouvons un fichier de données (fichier brest-obs.txt) indiquant les hauteurs d'eau observées heure par heure pour tous les jours de l'année 2001 pour le port de Brest. Nous en donnons un extrait ci-dessous, qui concerne les 30 premiers jours de 2001.

Source - © 2001 SHOM

Figure 4. Extrait des données de marées observées à Brest

Sur internet, nous retrouvons également les dates des phases de la Lune pour l'année 2001.

Première analyse

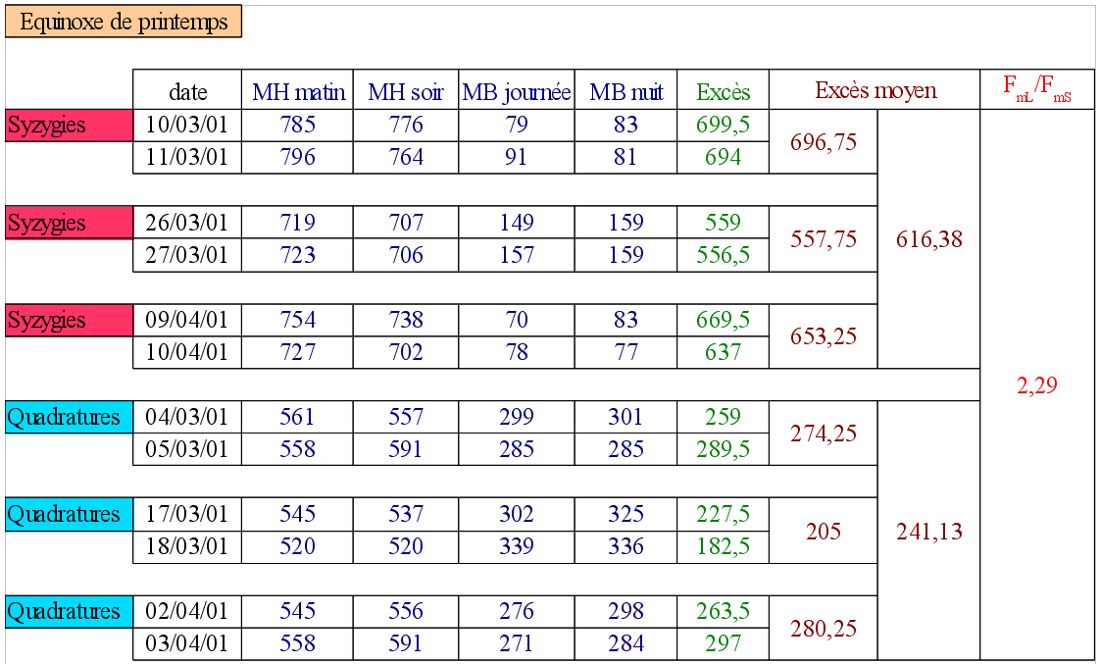
Nous regardons les hauteurs des marées lors des syzygies aux alentours de l'équinoxe de printemps (Pleine Lune le 9 mars et Nouvelle Lune le 25 mars). Ces marées des équinoxes sont les plus fortes de l'année. Les hauteurs d'eau sont données en cm, MH signifie marée haute et MB marée basse. L'excès est calculé en faisant la différence entre la somme des deux marées hautes quotidiennes et la somme des deux marées basses.

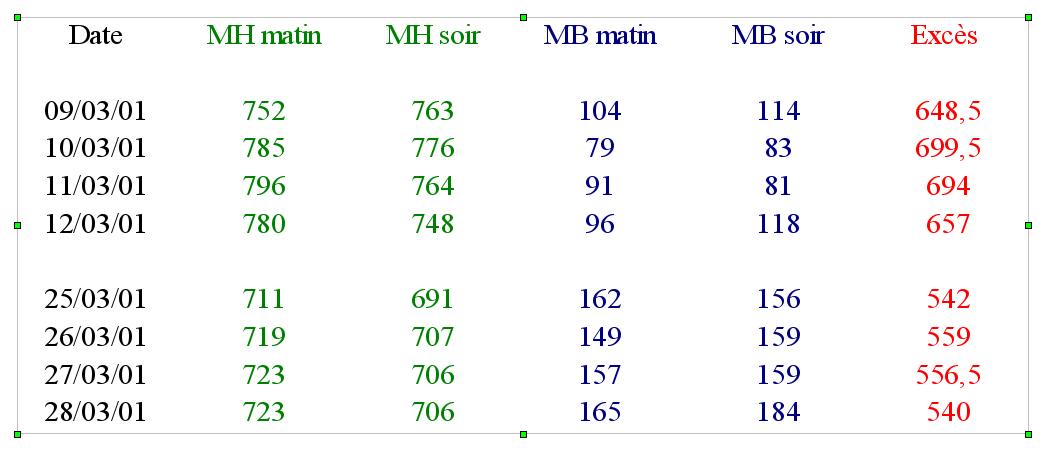
Figure 5. Extrait des données de marées observées à Brest

Traitement des données des marées lors des syzygies de mars 2001. MH signifie marée haute et MB marée basse. Hauteurs d'eau et excès donnés en cm.

Ces premiers calculs amènent deux constatations.

• Les plus fortes marées ne surviennent pas le jour même des syzygies mais le lendemain ou le surlendemain. De la même manière, la marée haute ne coïncide pas avec le passage de la Lune dans le méridien ou dans l'anti-méridien, de l'autre côté de la Terre, mais quelques heures plus tard. Ces retards montrent que les marées ne correspondent pas à des marées d'équilibre (notre hypothèse) mais sont perturbées par des phénomènes dynamiques (la rotation de la Terre entraîne le bourrelet de marée et la Lune "peine" à le ramener à son aplomb du fait de frottements des masses d'eau (on parle de retard à la déformation), ce qui explique qu'un lieu donné passe à l'aplomb de la Lune avant la marée haute, marée qui est donc en "retard").
• Il y a une très forte différence entre l'excès d'une syzygie à l'autre (on passe d'un excès de 7,0 m le 10 mars à un excès de 5,6 m le 26 mars, quinze jours plus tard). Ces différences proviennent essentiellement de la variation de la distance Terre-Lune. La Lune tourne en effet autour de la Terre sur une orbite elliptique, sa distance à la Terre varie considérablement. Ainsi le 9 mars, elle est située à 56,6 rayons terrestres de la Terre et le 25 mars à 62,3 rayons terrestres (nous trouvons ces informations sur le site internet de l'Institut de Mécanique Céleste et de Calcul des Éphémérides qui met à disposition un logiciel de calcul des éphémérides).

Conséquences à tirer de ces deux constatations.

• Nous ne calculerons pas directement l'excès de la marée haute sur la marée basse le jour des syzygies ni le jour des quadratures mais le lendemain et le surlendemain et nous prendrons la moyenne des deux jours.
• L'influence évidente de la distance Terre-Lune montre qu'il faut adopter une méthodologie adéquate pour analyser les observations. Nous nous servons du procédé de Laplace qui, en 1825, reprend la méthode de Newton en la perfectionnant.

Deuxième analyse avec l'aide de Laplace

Laplace remarque qu'un grand nombre de phénomènes perturbent les marées. Il explique que pour faire ressortir les phénomènes que l'on veut déterminer et augmenter nos chances de succès, il faut effectuer une combinaison avantageuse des observations. Nous exposons les différents points de notre méthodologie.

Prise en considération de l'excès de la haute mer sur la basse mer plutôt que simplement l'élévation de la marée haute. Par ce procédé, l'influence des conditions météorologiques (en particulier le vent) devient presque nulle : si le vent élève la hauteur d'une pleine mer, il élève à peu près autant la basse mer voisine et son effet disparaît dans la différence des deux hauteurs.

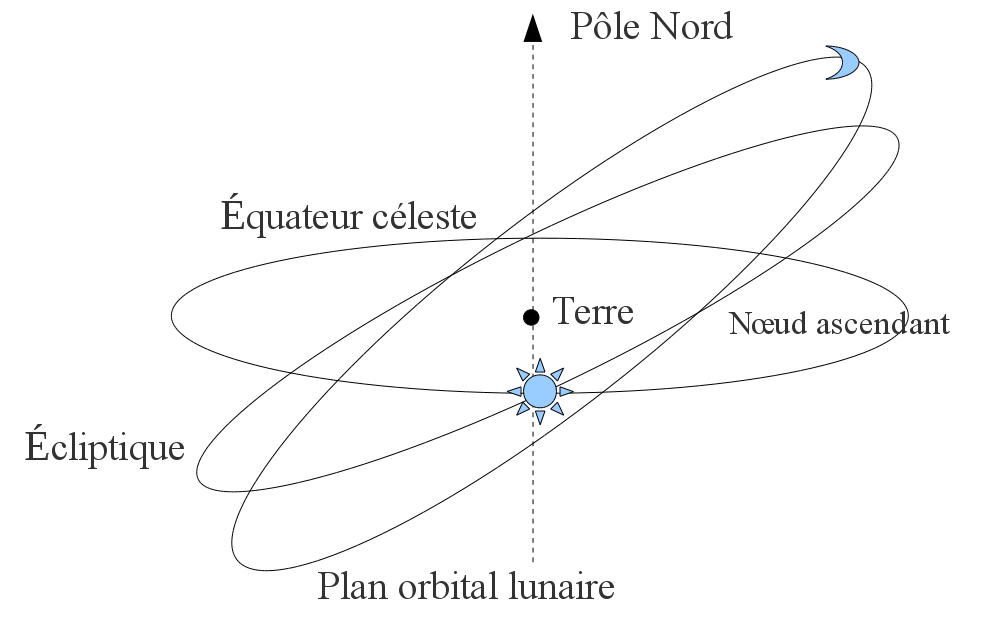
Choix du moment de l'année à considérer. Le moment des équinoxes est le plus judicieux car alors le Soleil est dans l'équateur céleste (plan perpendiculaire à l'axe Nord-Sud -axe Terre - étoile polaire-, passant par le centre de la Terre et contenant donc l'équateur géographique terrestre). La Lune est également à peu près dans l'équateur céleste au moment des Pleines et des Nouvelles Lunes d'équinoxes, elle a cependant une déclinaison au moment des premiers et des derniers quartiers qui perturbe son action (mais dont nous ne tiendrons pas compte).

Figure 6. Marées et positions relatives Terre - Lune- Soleil dans un repère géocentré

L'orbite de la Lune est légèrement inclinée par rapport à l'écliptique. Aux équinoxes, le Soleil est dans l'équateur céleste. Au moment des Pleines et des Nouvelles Lunes, la Lune est elle aussi à peu près dans l'équateur céleste (puisque la Terre, la Lune et le Soleil sont alignés), ce qui n'est plus le cas au moment des premiers et derniers quartiers.

Prise en compte de la variation de la distance Terre - Lune. Pour faire disparaître cette influence de la Lune, l'idée judicieuse de Laplace est de considérer trois syzygies (ou trois quadratures) consécutives autour des équinoxes et de faire la moyenne des excès en doublant la syzygie intermédiaire. Ainsi l'influence de la distance est moyennée car si la Lune est au périgée (plus proche distance de la Terre) lors d'une syzygie, elle sera à peu près à l'apogée (plus grande distance de la Terre) lors de la syzygie suivante.

Multiplication des observations. Pour améliorer les résultats, il conviendrait de ne pas travailler avec quelques observations isolées mais, au contraire, d'en utiliser un très grand nombre. Nous ne disposons cependant que des données de l'année 2001 et nous nous contenterons de faire la moyenne entre l'équinoxe de printemps et l'équinoxe d'automne pour cette année là.

Les résultats

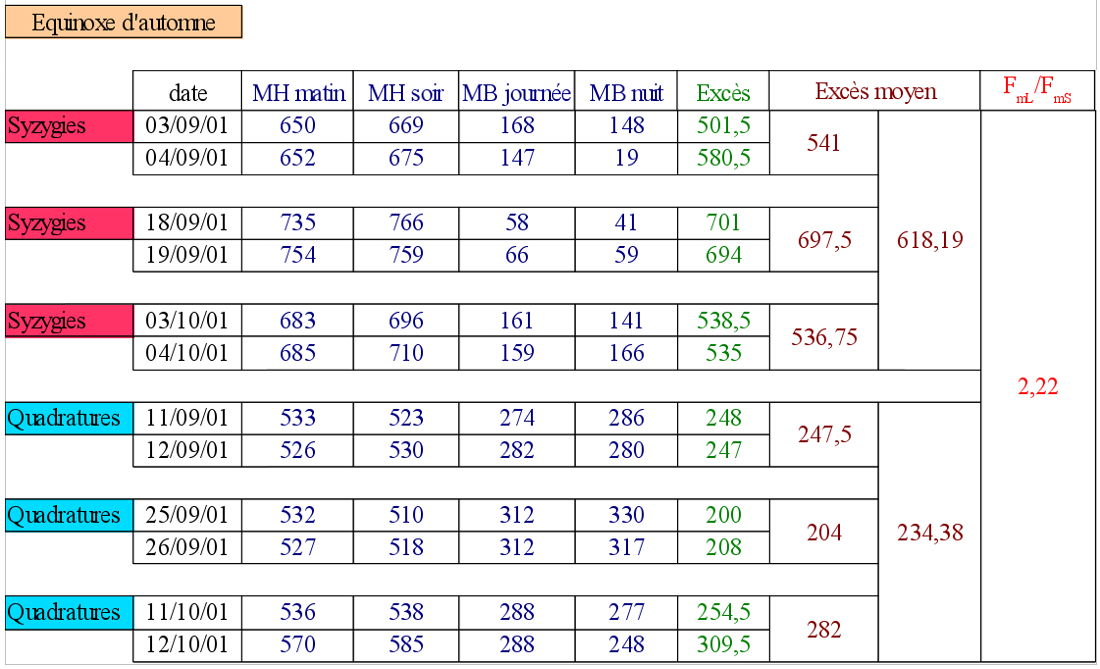
Pour l'équinoxe de printemps, nous étudions les syzygies du 8 mars, 25 mars et 8 avril (de l'année 2001) et les quadratures du 3 mars, 16 mars et 1^er avril. Pour l'équinoxe d'automne, nous étudions les syzygies du 2 septembre, 17 septembre et 2 octobre et les quadratures du 10 septembre, 24 septembre et 10 octobre.

Nous rappelons que le rapport des forces de marées lunaires sur les forces de marées solaires est calculé par : $\frac{h_{\mathrm{syz}}+h_{\mathrm{qua}}}{h_{\mathrm{syz}}-h_{\mathrm{qua}}}=\frac{F_{\mathrm{mL}}}{F_{\mathrm{mS}}}$.

Figure 7. Analyse des marées de l'équinoxe de printemps 2001

Figure 8. Analyse des marées de l'équinoxe d'automne 2001

La moyenne des résultats obtenus pour l'équinoxe de printemps et l'équinoxe d'automne donne : $\frac{F_{\mathrm{mL}}}{F_{\mathrm{mS}}}=\mathrm{2,25}$.

Malgré nos hypothèses très simplificatrices, le résultat est étonnamment proche de la valeur moderne (2,18). Pour savoir s'il s'agit d'un coup de chance ou si la méthode est robuste, il faudrait analyser les hauteurs de marées de plusieurs années différentes.