Activer le mode zen
Ressource au format PDF
Classification
L'expérience « laser-lune »
27/05/2011
Résumé
Un article du dossier « Les lasers en questions ». Mesure de la distance terre-lune par aller-retour d'une impulsion laser, principe, ordres de grandeurs.
Table des matières
Introduction
L'expérience « laser-lune » de l'Observatoire de La Côte d'Azur (OCA) a pour but la détermination précise de la distance terre-lune et de ses variations. Elle est située sur le plateau de Calern, près de Grasse.
Le principe est la mesure de la durée τ d'aller-retour d'une impulsion laser émise du sol terrestre vers un réflecteur lunaire. On en déduit la distance terre-lune D = cτ / 2. La valeur moyenne de la distance terre-lune étant d'environ 3,84.108 m, on prévoit un intervalle τ ≈ 2,56 s entre l'émission d'une impulsion et la réception du signal de retour correspondant. Actuellement, la distance D est déterminée au centimètre près, la précision atteinte sur la mesure de τ étant de δτ ≈ 10-10 s = 100 ps.
Figure 1. Laser de l'observatoire du CERGA
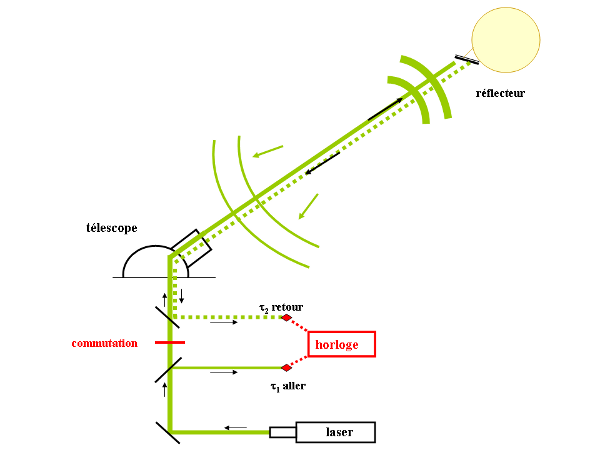
La figure 3 schématise les éléments de l'expérience.
Les détails sur l'instrumentation et l'analyse des mesures sont donnés sur les sites suivants : station de Télémétrie Laser-Lune - Observatoire de La Côte d'Azur ; centre d'analyse des données laser-lune SYRTE - Observatoire de Paris.
Des mesures similaires (lunar laser ranging, LLR) sont faites dans différents observatoires étrangers, notamment le récent projet APOLLO à Apache Point (Apache Point Observatory Lunar Laser-ranging Operation, Nouveau Mexique, USA). Un large réseau d'observatoires utilisent le même principe de télémétrie laser pour assurer le suivi précis des trajectoires de satellites artificiels (satellite laser ranging, SLR), la coordination se faisant à l'échelle internationale (International Laser Ranging Service). Les performances des mesures obtenues par laser-lune suscitent de nombreux développements et améliorations : voir par exemple à l'Observatoire de La Côte d'Azur la station de télémétrie laser MéO.
Dans cet article, nous abordons en particulier les deux questions suivantes :
- la proportion moyenne des photons détectés après réflexion sur la lune est inférieure à 1 sur 1019. Comment expliquer ce très faible rapport ?
- comment la traversée de l'atmosphère par le faisceau laser limite-t-elle la précision finale ?
Des applications numériques simplifiées permettent de comprendre certains des ordres de grandeurs des étapes de la mesure à partir des phénomènes physiques. Elles sont fondées sur les caractéristiques l'expérience française, décrites dans l'article détaillé Millimetric Lunar Laser Ranging at OCA de E. Samain et al, 1998, Astronomy& Astrophysics Supp. Series, 130, 235.
Proportion des photons détectés après réflexion
C'est la géométrie du faisceau laser et sa perturbation par la turbulence atmosphérique qui cause la perte de rayonnement entre l'émission de l'impulsion laser et la réception du signal réfléchi. Bien que très directif, un faisceau laser n'est jamais strictement parallèle. Il admet un petit angle d'ouverture θ qui est dû au phénomène de diffraction et dont la valeur est inversement proportionnelle à la dimension transversale du faisceau. La petitesse de l'angle θ caractérise la « cohérence spatiale » du faisceau. On a la relation usuelle θ =1,22 λ/d où d est le diamètre du faisceau (note 1).
Dans le cas du laser-lune la longueur d'onde est λ = 532 nm (laser YAG-Nd et doubleur de fréquence, lire à ce sujet l'article Laser dans l'ultra-violet). Le diamètre du faisceau à la sortie du laser est de 1,2 cm. Sa cohérence spatiale propre est donc caractérisée par l'angle θ ≈ 10 arcsec (note 2). Le faisceau laser passe par l'optique du télescope pour être dirigé vers la lune, ce qui élargit le faisceau laser et réduit son angle de divergence d'un facteur 5 environ. La prise en compte de l'effet de la turbulence, variable selon la qualité du ciel, détériore la cohérence et augmente la divergence d'un angle de l'ordre de 1 à 2 arcsec. En définitive la divergence effective du faisceau laser envoyé vers la lune est de 4 arcsec environ.
1. La relation usuelle θ = 1,22 λ/d donne la largeur angulaire à demie-intensité du cône de diffraction à l'infini d'une ouverture circulaire sur laquelle l'amplitude lumineuse est uniforme. Les lasers fournissent en général des faisceaux « gaussiens », l'amplitude sur la section de sortie diminuant exponentiellement en fonction du carré de la distance à l'axe. Dans ce cas, le coefficient de la relation est plus petit, en restant de l'ordre de grandeur de l'unité.
2. Il est commode d'évaluer les angles en unité de seconde d'arc (notée '' ou arcsec), car un angle 1 arcsec = 4,85.10-6 rad est un repère utile en astronomie : il représente la meilleure résolution spatiale possible des observations du ciel à partir du sol, du fait de la turbulence atmosphérique. La relation ci-dessus montre que c'est aussi la résolution angulaire théorique, limitée par la diffraction, d'un télescope de 13 cm de diamètre, pour la longueur d'onde λ = 532 nm.
Le faisceau laser atteint la lune avec une section de diamètre L1 = Dθ ≈ 7 km, où D est égale à la distance terre-lune (D ≈ 3,84.108 m). L'éclairement de la tache circulaire sur le sol lunaire a une structure irrégulière de type « speckle », due à la traversée de l'atmosphère terrestre. Le réflecteur lunaire est un panneau composé d'une mosaïque d'éléments catadioptriques, de type « coins de cube » (note 3). Compte tenu de l'efficacité de la rétro-reflexion et de l'inclinaison du panneau par rapport à la direction du laser, on peut considérer qu'il est équivalent à un miroir de diamètre ℓ1 ≈ 0,1 m. On évalue donc que la fraction réfléchie de la lumière laser, dans le rapport des deux surfaces, est approximativement égale à f1 = (ℓ1/L1)2 ≈ 2.10-10.
Source : NASA, Appolo XV Map and Image Library, image n° AS15-85-11468
Le faisceau de retour subit à nouveau un étalement angulaire, d'une part à cause de la diffraction par les éléments du réflecteur lunaire, d'autre part à nouveau par la traversée de l'atmosphère. Les « coins de cube » constituant le réflecteur ont une dimension de l'ordre du cm (note 3). Leur effet de diffraction produit un étalement du faisceau de l'ordre de 12 arcsec, plus important que celui de la turbulence atmosphérique. L'impact sur la terre couvre une surface de diamètre L2 ≈ 25 km. La fraction du faisceau réfléchi qui atteint le télescope de diamètre d2 = 1,54 m est donc au mieux égale à f2 = (d2/L2)2 ≈ 4.10-9.
La géométrie des faisceaux impose une limite au rapport entre les intensités reçue et émise : c'est la valeur du produit f1.f2 ≈ 8.10-19.
En tenant compte de l'atténuation dans l'atmosphère (absorption ou diffusion, ≈ 0,9), le filtrage spectral éliminant la lumière parasite (≈ 0,4), le rendement quantique de détection (≈ 0,2), on prévoit un facteur de retour d'environ 6.10-20.
Les mesures montrent qu'on ne détecte en moyenne qu'un seul photon de retour pour une centaine d'impulsions du laser émises en 10 s. Chaque impulsion du laser émet une énergie E = 0,3 J sur une durée de 0,3 μs (puissance-crête de 1 MW !). Pour une impulsion, le nombre de photons émis par le laser est N = E/hν = Eλ / hc = 0,8.1018. La fraction effective des photons détectés est donc en réalité encore plus petite, de l'ordre de 10-20.
3. Cinq réflecteurs furent déposés sur la lune par les missions Appolo et Lunakhod dans les années 1970. Les réflecteurs rétro-réfléchissants sont constitués d'une mosaïque d'éléments catadioptriques, dits « coins de cube », car constitués de trois petits miroirs plans perpendiculaires entre eux. Les valeurs numériques données ici sont celles du plus grand des réflecteurs, celui d'Appolo XV. Il est intéressant de signaler que le réflecteur Lunokhod-1 déposé en 1970 par l'automate de la mission soviétique Luna17 n'a pu être repéré que très récemment, en avril 2010 (UCSD Physicists Signal Long Lost Soviet Reflector on Moon).
Effet de l'atmosphère
Le faisceau laser traverse deux fois l'atmosphère, à l'aller et au retour.
D'une part la réfraction liée aux variations d'indice de l'air fait dévier légèrement le faisceau de la propagation rectiligne. Les fluctuations dues à la turbulence des masses d'air contribuent donc à la perte de photons entre l'émission et la réception (voir ci-dessus).
D'autre part on doit tenir compte du fait qu'une partie des trajets du faisceau laser s'effectue avec la vitesse de propagation de la lumière dans l'air cair = c0/n (voir l'article Laser et indice de l'air). L'indice n dépend de la densité, de la température et de l'humidité de l'air. C'est donc une fonction de l'altitude z qui peut varier en fonction du temps selon la pression atmosphérique et l'humidité de l'air.
La traversée de l'atmosphère ajoute un délai δτ par rapport à la durée de propagation du faisceau laser dans le vide. Il se déduit de la relation donnant l'augmentation du chemin optique :
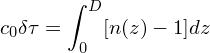 , pour un tir laser vertical.
, pour un tir laser vertical.
Lorsque le tir laser est incliné d'un angle β sur l'horizon (au zénith, β = 90°), ce délai est encore augmenté d'un facteur 1/sin β.
Avec cette correction, la mesure de la distance terre-lune D devient : D = c0 (τ - 2 δτ) / 2 = c0 τ / 2 - δD. Le terme correctif δD doit être évalué avec la même précision que celle à atteindre sur la mesure de D.
Pour un tir laser au zénith le terme δD est minimum, de l'ordre de 2 m (note 4). Il dépend aussi des conditions de pression, de température et d'humidité de l'air.
Des modèles d'atmosphère permettent d'évaluer avec une précision de l’ordre du millimètre la correction atmosphérique sur D en fonction des données du site d’observation et des conditions météorologiques.
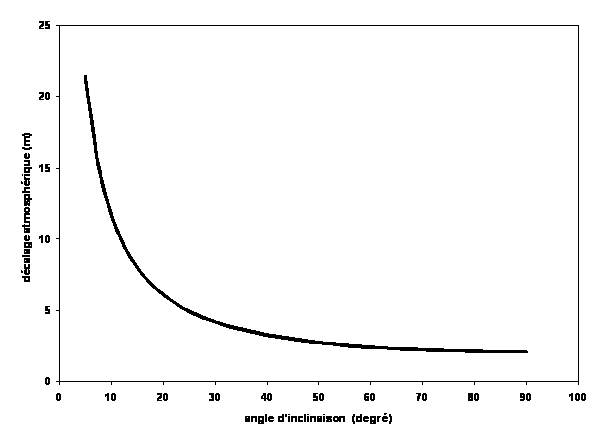
La figure 5 montre un exemple de variation de δD en fonction de l’angle β, pour des conditions usuelles sur le site de Grasse.
D’après les paramètres fournis par l’IERS (International Earth Rotation and Reference Systems Service), http://tai.bipm.org/iers/convupdt/convupdt_c9.html
4. On obtient une approximation simple du terme correctif pour un tir vertical.
On considère qu'à l'altitude z, la correction n(z)-1 sur l'indice de l'air est proportionnelle à la densité des molécules d'air, soit N(z) le nombre de moles par unité de volume, chacune ayant une masse M = 0,029 kg.
D'après la loi d'équilibre hydrostatique d'une tranche dz de l'atmosphère, on a la variation de pression : dP(z) = - M g N(z) dz où g est l'accélération de la pesanteur (supposée constante sur l'épaisseur de l'atmosphère).
Le supplément de trajet optique du faisceau dans l'atmosphère par rapport au trajet dans le vide s'obtient simplement par l'intégration suivante :
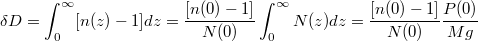
soit, en supposant la loi des gaz parfaits pour l'air à T = 288 K (constante R = 8,32 J.K-1) et avec n(0)-1 = 3.10-4
δD = [n(0)-1] RT(0)/Mg = 2,5 m
ce qui est en accord satisfaisant avec la valeur de la figure ci-dessus.
Conclusion
L'augmentation du nombre et des performances des mesures laser-lune permet une analyse de plus en plus précise de l'orbite et des mouvements de la lune. Les applications sont diverses, en astronomie, géophysique et physique fondamentale. Une meilleure connaissance de la dynamique de la lune, notamment de ses mouvement de « librations », renseigne sur sa structure interne (par exemple la caractérisation d'un coeur fluide au centre de la lune, à 20 % du rayon lunaire).
L'amélioration des éphémérides de la lune, c'est-à-dire la prédiction de sa position précise dans le ciel à chaque instant, a des implications plus générales en mécanique céleste. Elle permet d'affiner les systèmes de référence astronomiques qui sont à la base de l'étude des planètes ou astéroïdes, ainsi que celle des interactions terre-lune et de la dissipation due aux marées. Les éphémérides sont également largement utilisées pour la navigation spatiale.
Enfin, en atteignant la précision millimétrique, les mesures de la distance terre-lune offrent la possibilité de vérifier les lois physiques fondamentales de la gravité. Dans le cadre du test des nouvelles théories cosmologiques, il serait important de détecter d'éventuels très faibles écarts des mouvements du système terre-lune par rapport aux prédictions de la théorie de la relativité générale d'Einstein. Actuellement, considérant l'incertitude de 4 mm sur les mesures de la distance terre-lune, on trouve que les observations et les prédictions de la relativité générale sont compatibles jusqu'à la précision de 10-13. Par exemple l'écart relatif maximum est de 10-13 entre les valeurs de l'accélération du soleil sur l'orbite de la terre qui sont déduites du modèle observationnel d'une part et de la théorie de la relativité d'autre part.
Pour aller plus loin sur ce sujet, on pourra lire :
- « La lune au secours d'Einstein. Entre la relativité générale et les théories rivales, la distance Terre-Lune », Kenneth Nordtvedt, La Recherche, N°295 - 02/1997 ;
- « Lunar laser ranging science : Gravitational physics and lunar interior and geodesy », James G. Williams, Slava G. Turyshev, Dale H. Boggs, J. Todd Ratcliff, Advances in Space Research, Volume 37, Issue 1, 2006, Pages 67-71.
Pour citer cet article :
L'expérience « laser-lune », Marie-Christine Artru, mai 2011. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/laser-distance-terre-lune.xml