Activer le mode zen
Ressource au format PDF
Classification
Détermination de la température d'un support par méthode optique (2/2)
19/03/2018
Résumé
≪ Si vous regardez au-dessus d'une surface chaude, l'image apparaît souvent floutée à cause des fluctuations de densité de l'air chaud au-dessus de la surface. Peut-on déterminer la température de la surface en utilisant cet effet ? Quelle est la précision d'une telle mesure ? ≫. C'est ce problème qui a motivé l'étude présentée dans cet article.
Table des matières
Lire l'article précédent : Détermination de la température d'un support par méthode optique (1/2)
1. Mesure de la vitesse de montée des volutes
Il s'agit maintenant d'utiliser les films afin de remonter quantitativement à la vitesse de montée des volutes.
Pour ce faire, on utilise le mode spatio-temporel du logiciel ImageJ [1]. Cet outil permet de sélectionner une ligne horizontale ou bien verticale sur l'image, et de représenter côte à côte les allures de cette ligne sur les différentes images successives du film.
Comme on s'intéresse ici à un mouvement vertical, et que l'on souhaite s'affranchir des éventuels effets de bord, on sélectionne une ligne verticale au milieu de l'image.
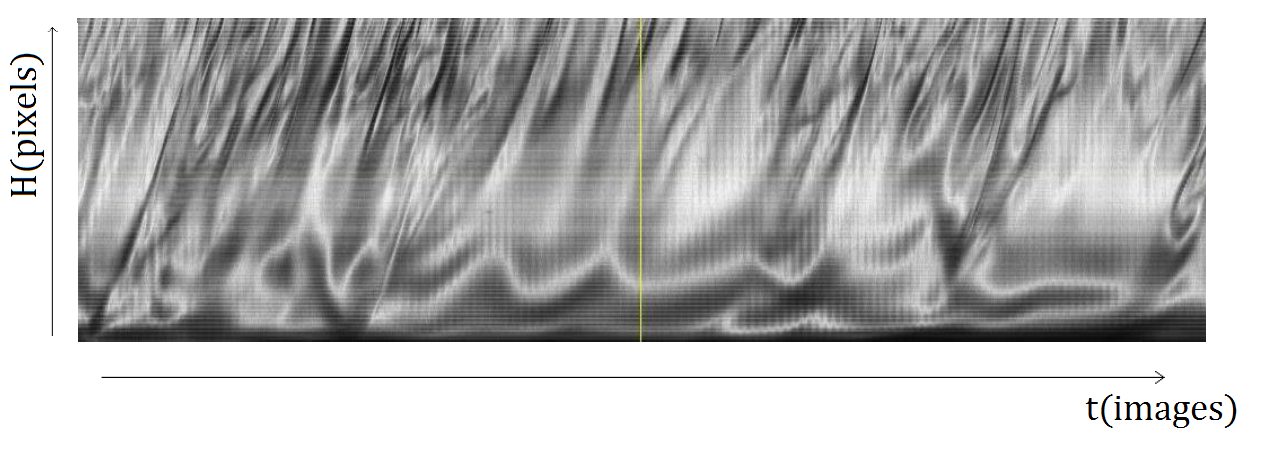
En la représentant horizontalement image par image, on obtient alors un diagramme spatio-temporel, comme celui représenté sur la figure 1.
 (a) Déplacement de la déformation du damier dans le temps en une abscisse donnée. En suivant la déformation, on peut retrouver la vitesse d’ascension du volute. (b) Diagramme spatio-temporel d'un bloc d'aluminium à T = 81 °C. Une ligne verticale, sur laquelle la hauteur peut se lire en pixels de la caméra, est représentée en fonction du temps croissant. On distingue une couche inférieure assez turbulente et une couche supérieure où on voit des taches noires et blanches gagner en altitude d'une image à la suivante, avec une vitesse (la pente des traits blancs montants) qui semble bien déterminée. Figure 1. Diagramme spatio-temporel |
L'intérêt du diagramme spatio-temporel est que l'on observe, au-dessus d'une couche limite de convection, une zone dans laquelle on voit nettement des volutes d'air chaud monter. La vitesse semble être proche pour les différents volutes ascendants (chacun correspond à un trait montant ici), ce qui en fait une grandeur pertinente pour un film donné.
Pour la mesurer, il reste à déterminer à quelle distance verticale effective au niveau du bloc correspond un certain nombre de pixels de la caméra. Pour cela, il suffit d'avoir pensé, au moment de tourner le film non perturbé par le bloc chaud, à disposer sur le côté de l'image une règle graduée verticale, au niveau bien sûr du support boy qui accueillera ensuite le bloc chaud. Le temps entre deux images est quant à lui simplement déterminé par la fréquence du film, ici 150 images/s, donc environ 6,67 ms entre deux images.
On pourra alors mesurer la vitesse de montée pour plusieurs traits, afin de calculer une moyenne pour un film donné, c'est-à-dire une température donnée. Il faudra ensuite répéter cette opération pour chacun des films pris, afin d'avoir la vitesse de montée des volutes en fonction de la température du bloc d'aluminium.
2. Présentation et commentaire des résultats
2.1 Vitesse d'ascension des volutes en fonction de la température
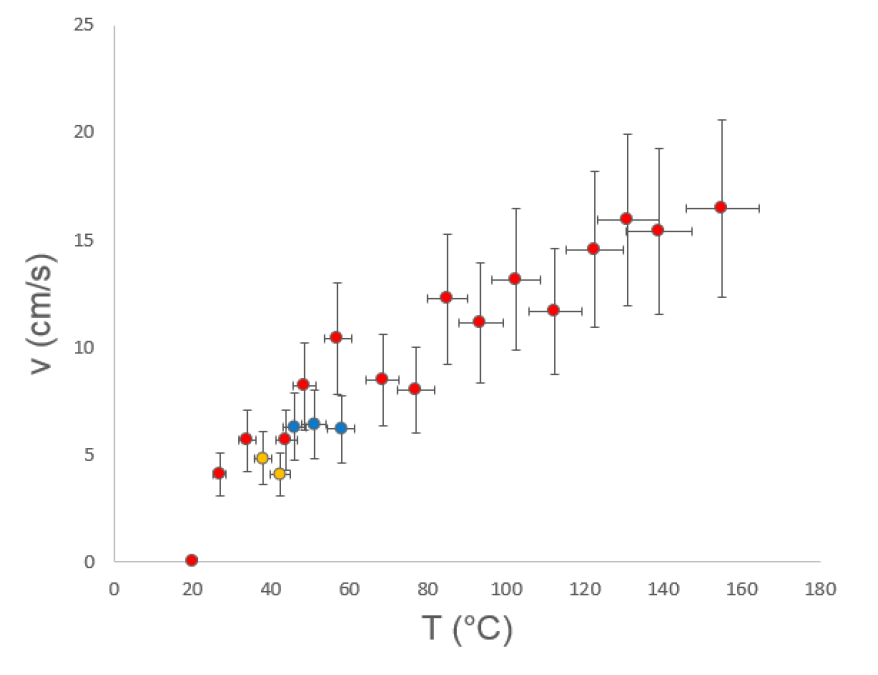
Le calcul de la vitesse v de montée des volutes à partir des films mène au graphique v = f (T),figure 2.
Sans surprise, on retrouve une vitesse nulle pour un bloc à température T = T0, puisque l'air surplombant ne reçoit pas d'énergie thermique du bloc. Sur le graphique, on trouve également des mesures effectuées pour deux autres matériaux (bois et PVC), avec des blocs de dimensions égales au bloc d'aluminium.
La convection ne dépendant pas a priori de la nature du matériau au contact de l'air, mais seulement de sa forme et de sa température : les points obtenus pour le bois et le PVC semblent se situer sur la même courbe que ceux obtenus pour l'aluminium.
 En rouge : les points obtenus pour le bloc d'aluminium, en jaune : ceux pour un bloc identique mais en bois et en bleu : ceux pour un bloc toujours identique mais en PVC. |
Les barres d'erreur sur la température proviennent de la variation de température indiquée par le thermocouple entre le début et la fin de l'enregistrement. Celles sur la vitesse proviennent de la dispersion statistique des différentes vitesses mesurées, par rapport à leur valeur moyenne. Sans surprise, ces deux sources d'incertitude augmentent avec T : un bloc plus chaud se refroidit plus vite et provoque une montée d'air plus turbulente. Les points semblent appartenir à une courbe globalement concave, que l'on peut difficilement approximer par une droite.
2.2 Modélisation du phénomène
Cette intuition est corroborée par le raisonnement énergétique suivant :
Un volute d'air donné (on admet que l'on peut le définir correctement) reçoit, dans la couche limite visible sur la figure 3, une énergie donnée par CV (T−T0), où CV est sa capacité thermique. Or on l'observe ayant un mouvement ascendant à la vitesse v, c'est-à-dire possédant une énergie cinétique donnée par mv2/2 où m est sa masse. Si on néglige, sur l'ascension filmée, ses variations d'énergie potentielle de pesanteur ainsi que sa déperdition de chaleur au profit de l'air environnant, on trouve que la vitesse de montée vérifie v2 ∝ (T − T0).
L'approximation faite ici est légitimée par le fait que sur la figure 3, les traits noirs et blancs semblent de pente constante. On peut alors tenter de tracer v2 en fonction de T.
 On distingue une couche inférieure assez turbulente et une couche supérieure où on voit des taches noires et blanches gagner en altitude d’une image à la suivante, avec une vitesse (la pente des traits noirs et blancs montants) qui semble bien déterminée. |
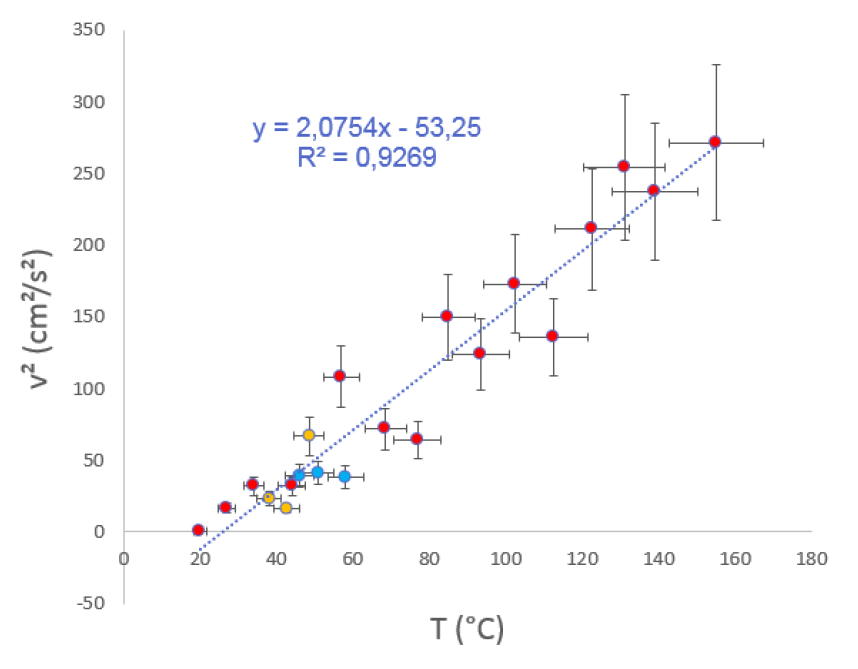
On obtient ainsi le graphique représenté sur la figure 4 : les points semblent ici alignés. Un ajustement affine donne un bon coefficient de corrélation et une annulation de v2 pour une valeur légèrement supérieure à T0, ce qui confirme notre analyse énergétique prévoyant v2 ∝ (T − T0).
On obtient donc une droite suffisamment robuste pour servir d'étalon à notre but initial, à savoir la mesure de la température T d'un support chaud à partir de mesures optiques sur le ≪ flou ≫ créé par un support chaud.
 En rouge : les points obtenus pour le bloc d'aluminium, en jaune : ceux pour un bloc identique mais en bois, et en bleu : ceux pour un bloc toujours identique mais en PVC. Un ajustement affine des données est représenté en pointillés, avec caractéristiques précisées en bleu. Figure 4. Allure de la courbe v2(T) obtenue |
3. Conclusion
Dans cet article, on a motivé et présenté une méthode expérimentale pour déterminer optiquement la température d'un support chaud, via la mesure de la vitesse de montée des volutes d'air chaud ascendants à son aplomb. Cette mesure est effectivement optique, puisque les volutes ont été traqués à l'aide de leur indice optique plus faible qui cause des déplacements apparents sur l'image d'un objet bien référencé. Les avantages principaux de cette méthode sont les suivants :
- Cette expérience est applicable à n'importe quel matériau constituant le support chaud comme on a pu le voir. Il faut tout de même que le support soit homogène : remarquons par exemple qu'une résistance chauffante en spirale n'établit pas une température uniforme sur un support horizontal ;
- Le protocole utilisé ici ne requiert aucunement que la lumière émise par le damier soit parallèle ou monochromatique. Il ne requiert pas non plus de travailler dans une pièce obscure, pour peu que le damier soit bien contrasté, ce qui le rend très aisé à mettre en place ;
- La précision sur la mesure de T à l'aide de la droite d'étalonnage obtenue est de l'ordre de 10 °C au maximum, et l'erreur relative sur T − T0 est presque toujours inférieure à 10%.
On pourra néanmoins se questionner sur les limites et prolongements suivants :
- La présence d'un courant d'air global au niveau de l'expérience peut être gênante et ajouter une vitesse fixe à tous les volutes. On peut s'en affranchir en apposant des panneaux de bois sur les côtés de la zone filmée ;
- Il faut adapter la taille des carreaux du damier à la longueur de la zone d'air chaud traversée : plus celle-ci est importante, plus la déviation moyenne des rayons l'est, et il faut s'efforcer de maintenir le côté d'un carreau au-dessus de cette déviation moyenne ;
- On peut également s'intéresser à l'air descendant au-dessous de blocs froids maintenus en l'air par des pinces bien isolées thermiquement : c'est une expérience dont la conception est symétrique de celle réalisée ici, et qui permettrait de tracer v2 pour T inférieure à T0 et ainsi de vérifier la symétrie attendue pour le graphe.
4. Protocole expérimental - Recommandations
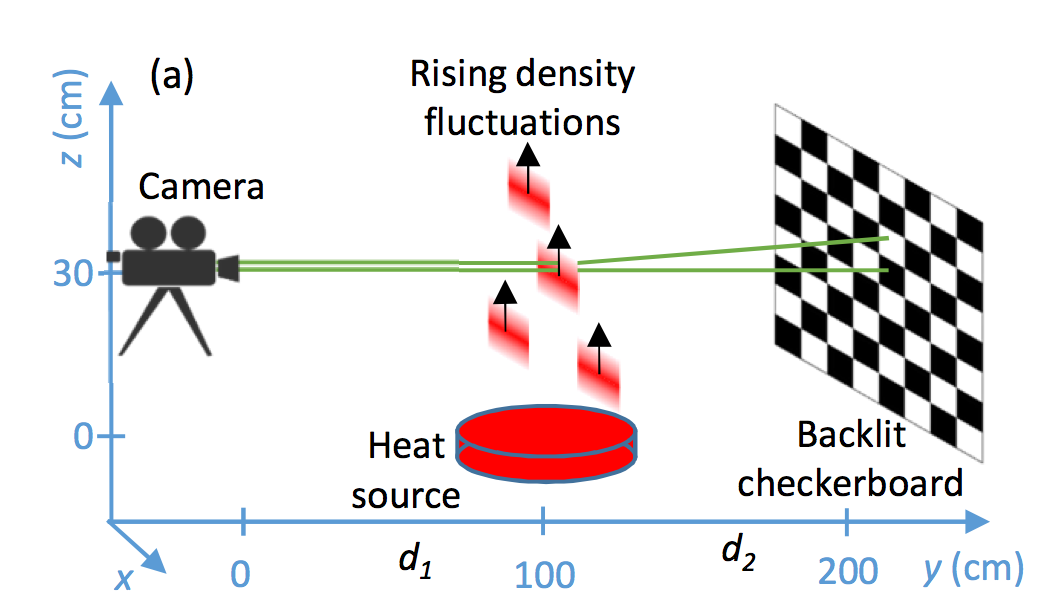
 Figure 5. Mise en œuvre expérimentale |
4.1 Choix du damier
On observe que certains carreaux du damier vont être en apparence déplacés verticalement ou horizontalement. La comparaison de ce film avec l'image de l'objet non perturbée par le support chaud permettra alors de voir où se situent les volutes d'air.
Plusieurs écueils se présentent néanmoins :
- Pour que la comparaison entre le film perturbé et une image non perturbée soit pertinente, il faut que le damier et la caméra soient fixes et que les carreaux soient tous de même dimension. Pour s'assurer de ce dernier point, on peut utiliser non pas un damier imprimé, mais un écran numérique affichant un damier, de sorte à avoir des carreaux faisant tous d par d pixels, avec d fixé pour tout le damier ;
- Si d est trop important, on verra bien les bords des carreaux bouger mais la distance entre deux déviations observables sera trop grande. La méthode employée ne nous donnera donc pas une cartographie précise des volutes d'air chaud.
- Si d est trop petit, la déviation typique d'un carreau risque d'être équivalente à la longueur de plusieurs carreaux alignés. On ne pourra alors plus dire quel est le carreau que l'on voit déplacé et il sera absolument impossible d'établir une cartographie précise des volutes d'air chaud.
Remarque sur le choix du damier
Au sujet du choix du pas du damier, le problème se retrouve par exemple dans l'observation de moirés (voir la vidéo de la Physique Animée : Superposition de phénomènes aléatoires : les moirés) ou encore lors d'observation de figures d'interférences. Par exemple dans le cas d'une figure obtenue à l'aide d'un interféromètre de Michelson, on ne peut pas connaître a priori l'ordre d'interférence.
Il y a donc un compromis à trouver sur d. Dans les expériences menées par la suite, nous avons travaillé avec d = 4 pixels. Ce choix permet d'avoir des carreaux plus grands que la déviation typique d'un pixel pour toutes les températures T de support que nous avons expérimentées, c'est-à-dire une gamme allant de 20 °C à 160 °C, dans une pièce à T0 = 20 °C.
4.2 Enregistrement des films
En ce qui concerne l'enregistrement des images, nous avons choisi d'utiliser une petite caméra Ximea noir et blanc, munie d'un objectif et capable de filmer à 150 images par seconde. Cette fréquence nous permet d'avoir une bonne précision sur la dynamique des volutes, qui montent avec des vitesses de l'ordre de 10 cm/s.
Les films obtenus par cette méthode ne permettent pas une analyse à l'œil nu, figure 6. Par contre, en imposant un contraste maximal à l'aide d'ImageJ, puis un flou gaussien, on arrive à la fois à rendre plus intenses et légèrement plus étendues ces figures blanches. Pour rendre l'expérience plus spectaculaire, on peut utiliser des niveaux de rouge plutôt que des niveaux de gris. Ceci permet d'obtenir des films tout à fait probants : figure 7.
4.3 Supports chauffés
En guise de support chaud, nous avons opéré avec des blocs d'aluminium cylindriques chauffés dans une étuve. Notons qu'un four de cuisine convient également très bien.
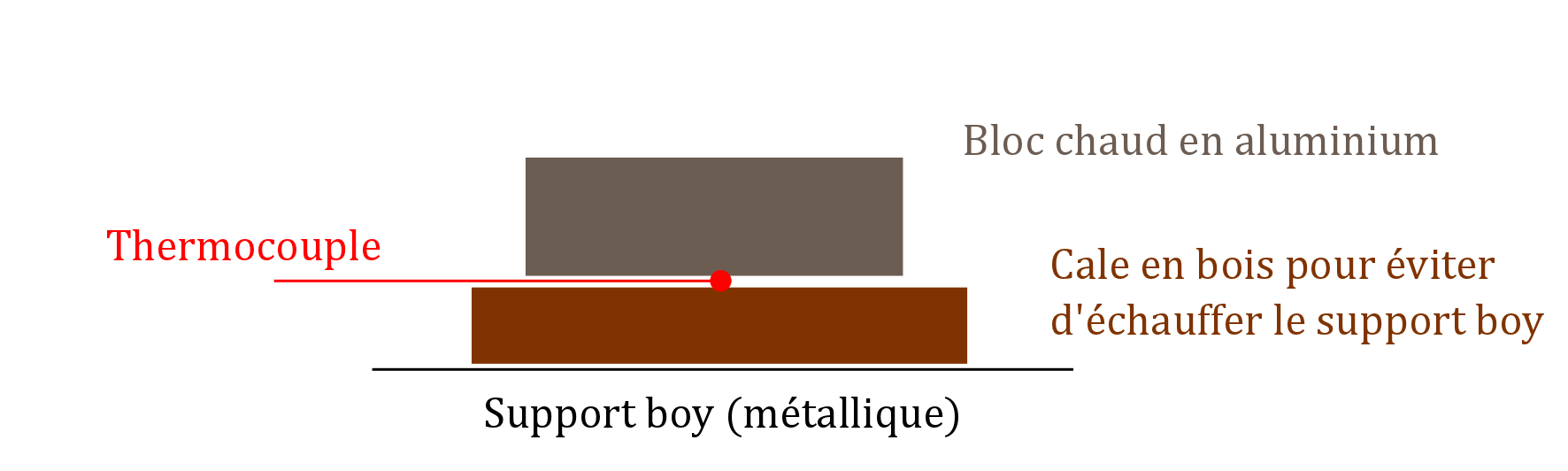
La taille du bloc est contrainte : il doit être de diamètre suffisant (au moins 10 cm) pour avoir une zone d'air chauffé suffisamment large, et pouvoir ainsi négliger les effets de bord sur le film. Il doit également ne pas être trop épais (moins de 5 cm, typiquement) afin de pouvoir être considéré à température quasi-uniforme après un temps de chauffe raisonnable. Cette considération est due au fait que pour quantifier la pertinence de l'expérience, nous avons également mesuré la température du support chaud, c'est-à-dire du bloc, à l'aide d'un thermocouple d'enseignement. Afin de ne pas perturber la dynamique de l'air surplombant, le thermocouple a été placé sous le bloc, ce qui permet au passage de le maintenir bien appuyé contre celui-ci, figure 8.
L'expérience est assez sensible au bruit vibratoire ambiant : un léger choc contre la table d'appui de la caméra (ou celle du damier) provoque déjà une déviation apparente des pixels du damier filmé.
Pour prendre l'image non perturbée du damier, nous avons filmé celui-ci une trentaine de secondes puis calculé, à l'aide du logiciel ImageJ, une image moyenne sur ce film (le logiciel calcule la moyenne des niveaux de gris obtenus pour chaque pixel de la caméra). Ce processus de moyennage a pour but de lisser l'éventuel bruit mécanique ambiant. On obtient donc une image de référence pour le damier.
On place ensuite le bloc d'aluminium, chauffé à 160 °C sur un support boy disposé entre le damier et la caméra. On a toutefois pris garde d'insérer une planchette de bois entre le bloc et le support boy, afin d'éviter que ce dernier ne s'échauffe aussi et ne crée ses propres mouvements de convection. Inutile de préciser que des gants anti-chaleur sont nécessaires pour transporter le bloc d'aluminium de l'étuve au support. On attend un peu (10 secondes suffisent), afin de laisser au mouvement de convection le temps de s'établir, puis on lance l'acquisition d'un film d'une trentaine de secondes environ. On relève vers le milieu de l'acquisition la température indiquée par le thermocouple que l'on a pris soin d'insérer entre la planchette et le bloc d'aluminium. Cette température doit être relevée vers le milieu du film afin de minimiser l'erreur de mesure. En effet, la température du bloc d'aluminium diminue durant le film, puisqu'il cède de l'énergie thermique à l'air qui le surplombe (c'est justement ce qu'on cherche à observer !) et à T = 160 °C dans une pièce à T0 = 20 °C, ce processus est assez efficace pour être sensible sur la durée du film.
Maintenant, il suffit de laisser le bloc refroidir et de relancer plus ou moins souvent (tout dépend du nombre de points souhaité) des films d'une trentaine de secondes, tout en relevant à chaque fois la température vers le milieu du film. On retrouve ici que pour que ce relevé reste pertinent, il faut un bloc pas trop épais.
5. Pistes d'exploitation
[1] ImageJ, logiciel libre, codé en Java, multiplateforme, qui permet le traitement et l'analyse d'images. https://imagej.net/Welcome
Pour citer cet article :
Détermination de la température d'un support par méthode optique (2/2), mars 2018. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/determination-temperature2-2.xml
