Activer le mode zen
Ressource au format PDF
Mots-clés
- rhéologie
- fluide newtonien
- fluide complexe
- écoulement
- contrainte
- cisaillement
Classification
Comment les fluides coulent-ils ?
11/04/2011
Résumé
Description des différents comportements des fluides sous cisaillement. Fluides newtoniens et fluides complexes.
Table des matières
L'eau et l'air sont de loin les fluides les plus présents dans la vie courante. Les propriétés de ces fluides usuels sont connues depuis des siècles. Il existe cependant de nombreux domaines dans lesquels des fluides dit complexes (ayant un comportement plus riche que les fluides usuels) revêtent une importance cruciale : l'écoulement du sang, du pétrole, des plastiques fondus, des gels à cheveux, du dentifrice ou encore des diverses préparations culinaires en sont des exemples.
Cellule de cisaillement
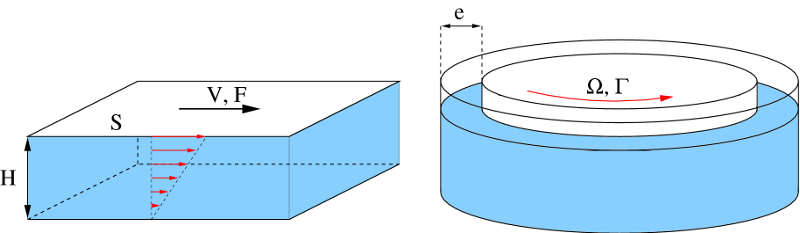
Afin de caractériser l'écoulement d'un fluide, les physiciens et ingénieurs étudient son comportement sous cisaillement. Il s'agit de placer une couche du liquide entre deux plaques parallèles et de faire avancer l'une des deux plaques (la plaque supérieure sur la figure 1 gauche). On peut choisir d'imposer la force F appliquée à la plaque mobile ou la vitesse de déplacement V. Le fluide étudié est alors cisaillé par les plaques planes parallèles. Cette géométrie est nommée cisaillement plan-plan.
Simple pour les simulations numériques, cette géométrie est difficilement utilisable expérimentalement car l'on rencontre des problèmes aux bords de la cellule : soit on place des parois verticales qui peuvent modifier l'écoulement, soit le fluide peut s'échapper de la cellule de cisaillement. On utilise souvent une géométrie différente : la cellule de Couette (figure 1 à droite). Elle est constituée de deux cylindres concentriques dont la différence de rayon e est appelée gap (écartement en anglais). Comme dans le cas de la cellule plan-plan, on impose au cylindre intérieur soit une vitesse de déplacement (ici une vitesse de rotation Ω), soit une force (ici un couple Γ). En pratique, le gap est souvent choisi petit (quelques millimètres) par rapport au rayon des cylindres afin de s'approcher au mieux d'une géométrie plane et d'éviter l'apparition d'instabilités.
À gauche, cellule plan-plan : le fluide est compris entre deux plaques parallèles distantes de H. La plaque supérieure se déplace à vitesse V et subit une force F. À droite, cellule de Couette : le fluide est compris entre deux cylindres concentriques distants de e. Le cylindre intérieur est en rotation à vitesse Ω et subit un couple Γ.
L'étude des écoulements, science nommée rhéologie, consiste à mesurer le lien entre déformation (ou vitesse de déformation) d'une part, et contraintes (c'est-à-dire les forces) d'autre part.
Dans le cas de la cellule plan-plan, la force nécessaire pour cisailler le fluide est proportionnelle à la surface S des plaques et l'on préfère ainsi définir la contrainte : σ = F/S (mesurée en Pascal). De plus, la grandeur pertinente pour caractériser l'intensité du cisaillement n'est pas la vitesse V mais la vitesse rapportée à l'épaisseur H. On définit ainsi le taux de cisaillement : γ̇ = V/H (mesuré en s-1).
Dans la géométrie de Couette, on peut choisir soit d'imposer le couple grâce à un moteur (c'est à dire la contrainte) et de mesurer la vitesse de rotation (c'est à dire le taux de cisaillement), soit d'imposer la vitesse de rotation et de mesurer le couple nécessaire pour y arriver. De façon générale, la rhéologie consiste à relier la contrainte σ au taux de cisaillement γ̇.
Fluides newtoniens
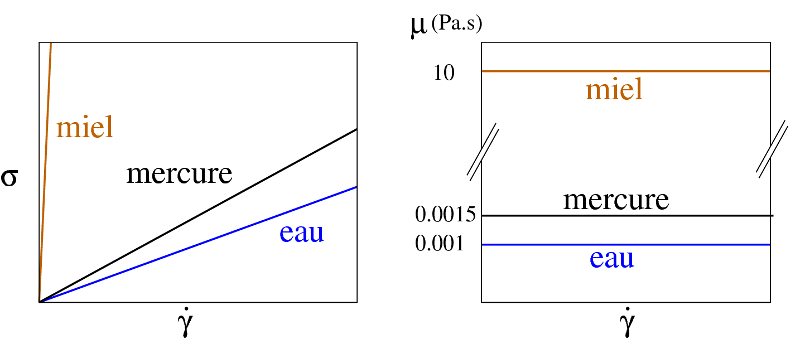
Les fluides usuels présentent une relation simple entre contrainte et taux de cisaillement : ils sont proportionnels. Le coefficient de proportionnalité est appelé viscosité dynamique μ et l'on peut écrire : σ = μ γ̇. La viscosité se mesure en Pa.s. Les fluides qui vérifient cette relation de proportionnalité sont dit fluides newtoniens. On peut résumer ces propriétés en traçant σ en fonction de γ̇, ou de façon équivalente la viscosité µ = σ/γ̇ (voir figure 2 pour quelques fluides usuels). Il faut noter que ces grandeurs peuvent varier fortement avec la température du fluide.
Fluides complexes
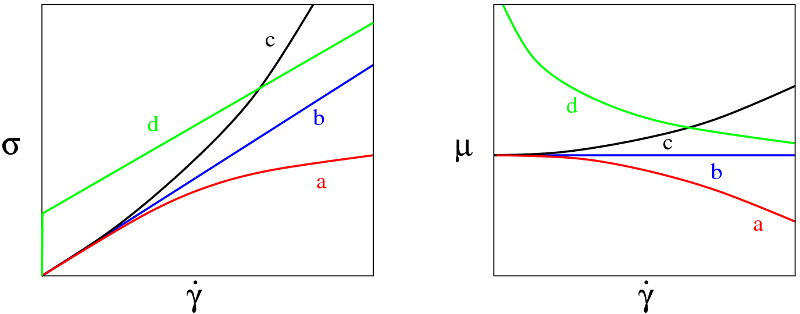
Si la majorité des fluides constitués de molécules simples ont un comportement newtonien, de nombreux autres fluides (dit non-newtoniens) n'obéissent pas à cette relation. Il s'agit des fluides complexes qui sont souvent constitués de molécules longues (polymères), de molécules chargées (farine de maïs comme celle vendue par la marque Maïzena) ou encore d'un mélange d'eau et de constituants « solides » (boues) ou biologiques (le sang). De façon générale, la viscosité effective de ces fluides, définie comme le rapport entre contrainte et taux de cisaillement µ = σ/γ̇, peut dépendre de nombreux paramètres physiques et peut par exemple évoluer avec le temps. Nous allons nous intéresser plus particulièrement aux fluides dont la viscosité ne dépend que du taux de cisaillement mais ne reste pas constante. On peut classifier ces fluides en trois catégories résumées sur la figure 3.
Fluides Newtoniens (b) : On reconnait le comportement des fluides newtoniens sur les courbes (b) de cette figure : la relation entre contrainte et taux de cisaillement est linéaire et la viscosité donc constante. De nombreux fluides courants tombent dans cette catégorie : l'eau, l'air, les huiles alimentaires...
Fluides rhéo-fluidifiant (a) : Le cas des courbes (a) est plus intéressant : lorsque l'intensité du cisaillement augmente, la contrainte est plus faible que celle d'un fluide newtonien, c'est-à-dire que la viscosité diminue. Ces fluides sont ainsi appelés rhéo-fluidifiants : plus on les cisaille, plus ils s'écoulent facilement. De nombreuses solutions de polymère présentent cette caractéristique. Une application pratique a été trouvée dans les peintures : le caractère rhéo-fluidifiant permet d'étaler facilement la peinture sur un mur car il est fortement cisaillé par le pinceau et il empêche la formation de gouttes ou de coulures car la viscosité augmente fortement lorsque le cisaillement diminue, c'est-à-dire lorsque l'on retire le pinceau.
Le sang est également un exemple bien connu de fluide rhéo-fluidifiant. Cette propriété est très intéressante pour la circulation sanguine car elle facilite l'écoulement du sang à travers les capillaires et autres artérioles les plus fins. En effet, le faible diamètre des capillaires induit un accroissement du taux de cisaillement ce qui rend le sang plus fluide et aide ainsi la circulation.
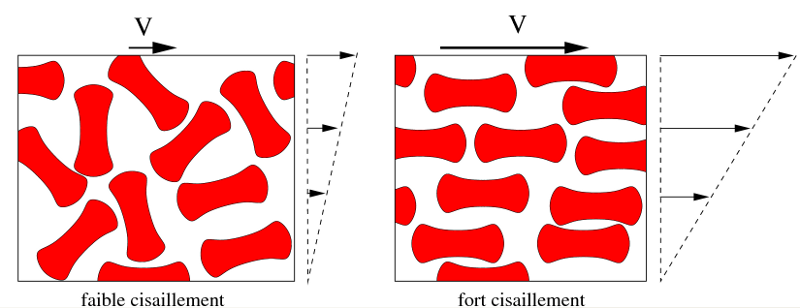
L'explication microscopique du caractère rhéo-fluidifiant réside dans la composition du sang qui est assimilable à de l'eau chargée de nombreux composants biologiques dont l'un des plus importants est le globule rouge. Les globules rouges (ou érythrocytes) sont fortement anisotropes : ils ont la forme d'un ballon de football dégonflé (voir figure 4). Lorsque le cisaillement est faible, l'orientation des globules est aléatoire mais lorsque le cisaillement augmente, ils s'alignent dans le sens de la circulation. De plus, sous fort cisaillement, les globules rouges ont tendance à s'agréger en rouleaux ce qui diminue encore la viscosité. L'écoulement est ainsi facilité par l'organisation microscopique du fluide complexe (figure 5).
Figure 4. Écoulement du sang | Figure 5. Écoulement du sang |
Fluides rhéo-épaississants (c) : à l'inverse des courbes (a), les courbes (c) sont caractéristiques des fluides dont la viscosité augmente lorsqu'ils sont fortement cisaillés. Ils deviennent ainsi plus « épais », d'où l'appellation rhéo-épaississant. Ce type de fluide est plus rare mais il existe quelques exemples bien connus. Le premier est une solution aqueuse concentrée de farine de maïs. Ce fluide est très facile à préparer : il suffit d'ajouter graduellement une petite quantité d'eau à la farine en remuant doucement avec une cuillère jusqu'à ce que le mélange présente un aspect liquide. On peut alors aisément constater le caractère rhéo-épaississant du fluide en le remuant avec une cuillère ou une fourchette : si l'on remue doucement, le fluide offre une résistance proche de celle de l'eau alors que si l'on tente de remuer énergiquement, le fluide offre une résistance digne du plus visqueux des miels.
Un autre exemple de fluide rhéo-épaississant sont les sables mouvants. Les histoires racontent que lorsque que l'on tombe dans les sables mouvants, plus on se débat et plus il est difficile d'en sortir. En effet, les sables mouvants (constitué essentiellement d'eau et de petits grains de sable) sont des fluides rhéo-épaississants : plus l'on s'agite et plus la viscosité du milieu est grande. Pour s'en sortir, il faut tirer lentement et avec constance sur les jambes et autres pieds pris au piège. On pourra remarquer que le danger des sables mouvants n'est pas d'y couler (ce qui est impossible en vertu de la poussée d'Archimède qui interdit que le corps humain, moins dense que de l'eau chargée de sable, ne coule dans ce milieu) mais de mourir de noyade, pris au piège lorsque la marée monte.
Le caractère rhéo-épaississant des suspensions de grains de sable dans l'eau trouve son origine microscopique dans la résistance hydraulique qu'offrent les grains à l'écoulement de l'eau. Lorsque l'on cisaille fortement le fluide, l'eau cherche à s'écouler entre les grains. Or deux des caractéristiques principales des sables mouvants sont leur forte concentration en grains, ainsi que la faible taille de ces derniers (de l'ordre de quelques dizaines de μm). Les grains constituent ainsi un milieu poreux, dont les interstices sont étroits et peu nombreux, ce qui offre une grande résistance à l'écoulement de l'eau comme la figure ci-dessous l'illustre.
Fluides à seuil (d) : La dernière catégorie des fluides complexes est celle des fluides à seuil. Comme on peut le voir sur la figure 3 gauche, pour un tel fluide le taux de cisaillement reste nul tant que la contrainte n'a pas atteint une valeur critique nommée contrainte seuil. En dessous du seuil, la viscosité correspondante est infinie car la contrainte peut être non nulle alors que le taux de cisaillement est rigoureusement nul. Ces fluides peuvent ainsi supporter une contrainte tout en résistant à l'écoulement. Quelques exemples sont les gels à cheveux, la mousse à raser ou encore le dentifrice. En effet, pour faire sortir le dentifrice de son tube, il faut exercer une certaine pression : si la pression est trop faible, le dentifrice ne sort pas. Une autre démonstration de l'existence de la contrainte seuil réside dans le fait que ces fluides peuvent rester « solides » sur un plan incliné. Si l'inclinaison est trop faible, la contrainte de cisaillement (ici la projection du poids le long du plan) est inférieure à la contrainte seuil et le fluide ne s'écoule pas. Contrairement aux fluides newtoniens, rhéo-fluidifiants ou rhéo-épaississants qui s'écouleront et s'étaleront au bout d'un certain temps, un fluide à seuil peut se maintenir sur une surface inclinée et conserver une forme.
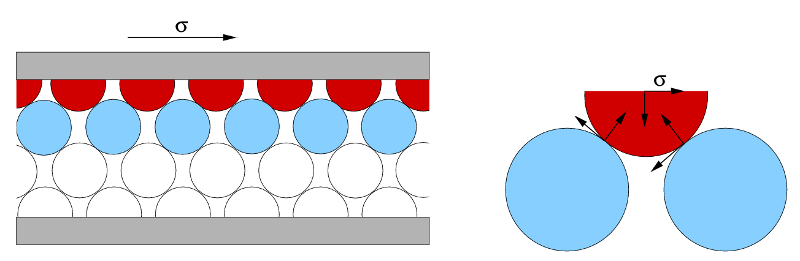
Un autre exemple de fluide à seuil est le sable sec. En effet, un empilement de sable peut conserver une surface non plane et non horizontale, de même qu'une couche de sable posée sur un plan faiblement incliné y restera indéfiniment. Étudions l'exemple d'empilement de grains de la figure 7 où l'on applique une force à la plaque supérieure. Les grains de la couche rouge cherchent à avancer par rapport à ceux de la couche bleue (on cherche à cisailler le milieu). Ils subissent de la part des grains bleus une force dirigée vers le haut (la réaction normale) et vers la gauche (réaction tangentielle). Ainsi, pour avancer, les grains rouges doivent surmonter les grains bleus (et donc vaincre la gravité) mais aussi vaincre les frottements. Cet exemple illustre le fait que l'on peut exercer une contrainte non nulle sans que celle-ci ne provoque d'écoulement. Dans ce modèle simple on peut calculer géométriquement la contrainte seuil et en déduire l'angle maximal d'un tas de sable.
Le même genre d'analyse géométrique permet d'expliquer l'existence d'une contrainte seuil dans les mousses dites sèches (de type de la mousse à raser). Une mousse sèche est constituée de cellules polyédriques remplies d'air et dont les faces sont constituées de films liquides. La figure ci-dessous est un exemple d'une mousse bidimensionnelle réalisée entre deux plaques de verre. Pour que la mousse soit cisaillée, il faut que le réseau de polyèdres se réarrange. Or celui-ci présente une certaine élasticité pour de faibles contraintes et de faibles déformations. Il se déforme alors de façon réversible, c'est-à-dire qu'il retrouve sa forme initiale lorsque la contrainte est relâchée. Il faut ainsi que la contrainte de cisaillement soit suffisamment importante pour franchir le seuil d'irréversibilité et provoquer un écoulement.
Conclusion
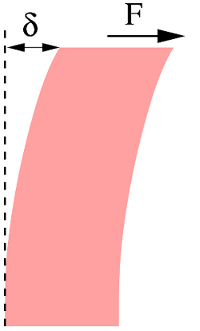
Les comportements présentés dans cet article sont des comportements idéaux et ne reflètent pas entièrement la complexité de la réalité. Une des complications observée est que la viscosité n'est pas toujours une fonction monotone du taux de cisaillement. De nombreux fluides sont rhéo-épaississants pour des forts taux de cisaillement alors qu'ils sont rhéo-fluidifiants aux faibles taux de cisaillements. D'autre part, la contrainte seuil des fluides à seuil est souvent très délicate à mesurer et parfois même à définir tant le comportement limite aux faibles taux de cisaillement s'éloigne de la vision schématique de la figure 3. La liste des nuances à apporter à la description faite ici serait longue, mais il existe une caractéristique majeure des matériaux réels qui n'a pas été abordée dans cet article. Nous avons fait l'hypothèse que la contrainte ne dépendait que de la vitesse de déformation (le taux de cisaillement), ce qui est caractéristique d'un fluide. À l'inverse, les solides élastiques sont caractérisés par une contrainte qui dépend directement de la déformation (et non plus seulement de sa vitesse de déformation). C'est le cas d'une gomme que l'on tient verticalement et que l'on soumet à un cisaillement (figure ci-contre) : pour de faibles déformations δ, la force est proportionnelle à δ. La gomme se comporte donc comme un ressort. Ces deux comportements idéaux (fluide visqueux et solide élastique) constituent une bonne approximation pour certains matériaux (comme l'eau ou le caoutchouc) mais le comportement réel de nombreux matériaux est intermédiaire : selon la contrainte, la déformation ou le taux de déformation, ils peuvent présenter un comportement fluide, solide ou intermédiaire. Ces matériaux sont ainsi appelés visco-élastiques et seront présentés dans un article futur. | Figure 9. Solide élastique sous cisaillement |
Pour citer cet article :
Comment les fluides coulent-ils ?, Nicolas Taberlet, avril 2011. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/comment-coulent-les-fluides.xml