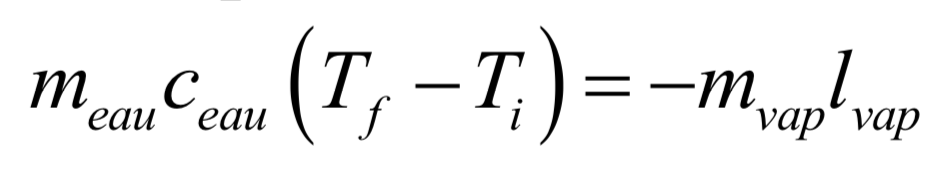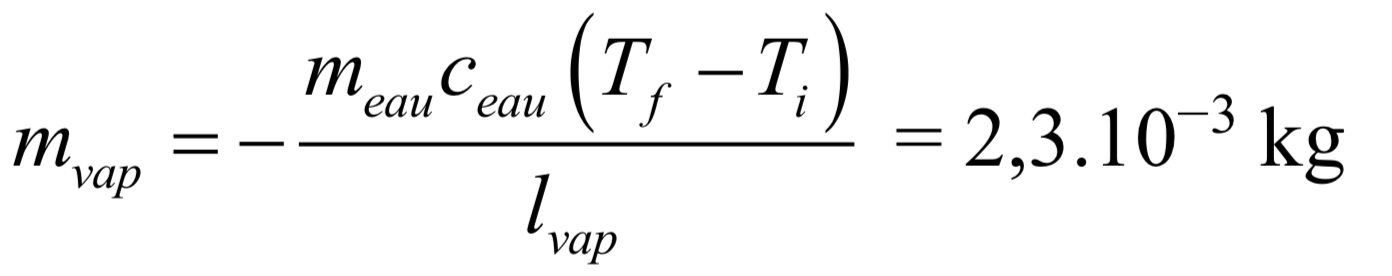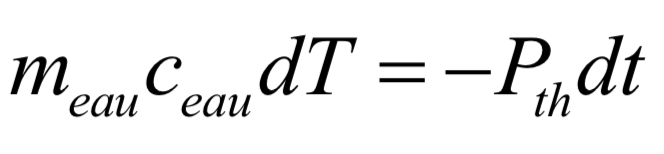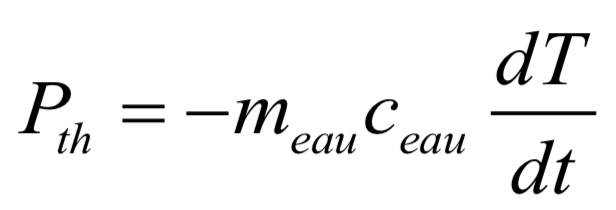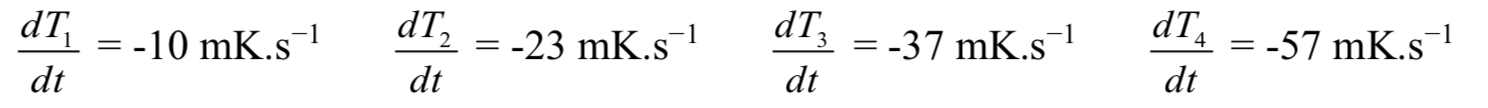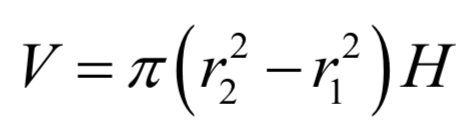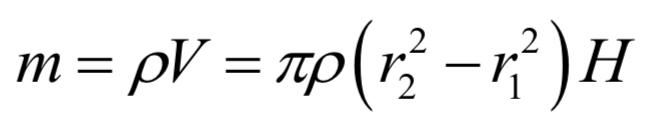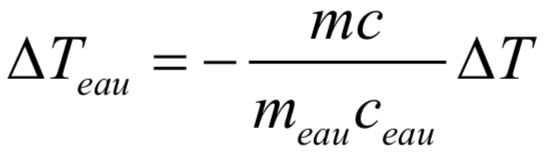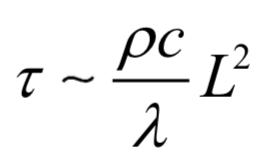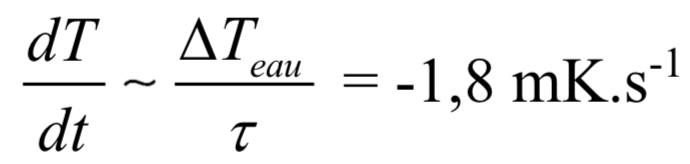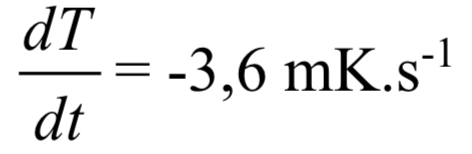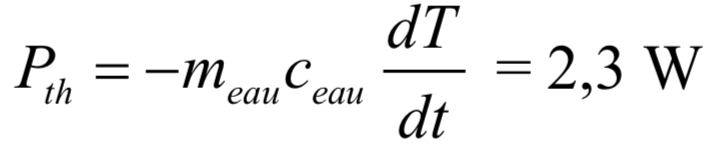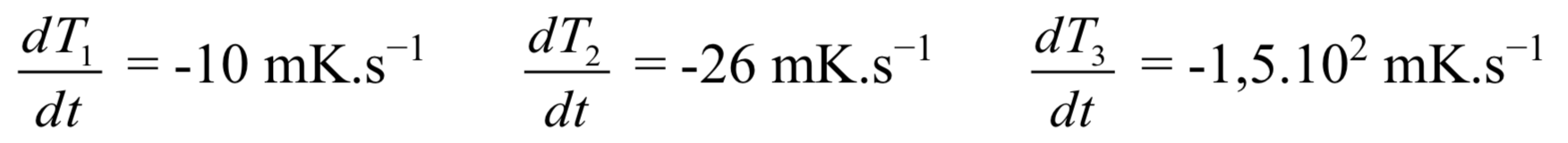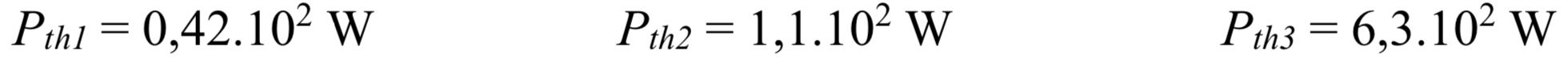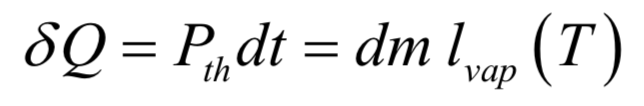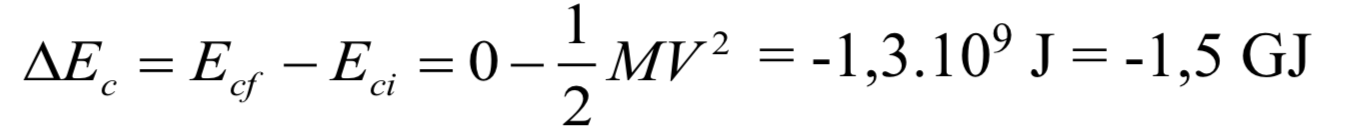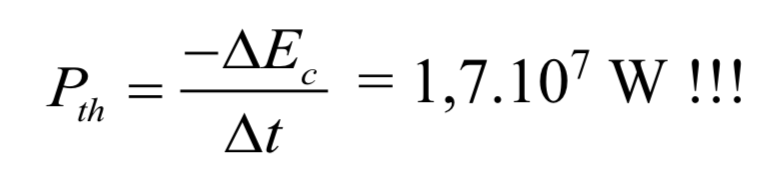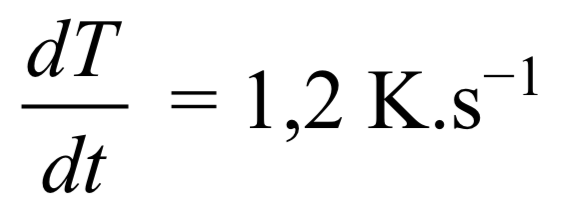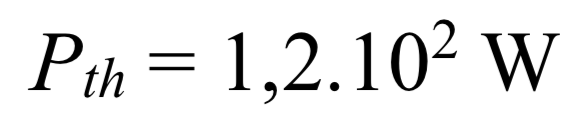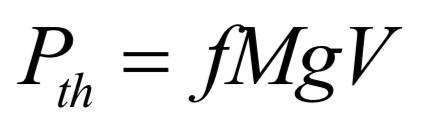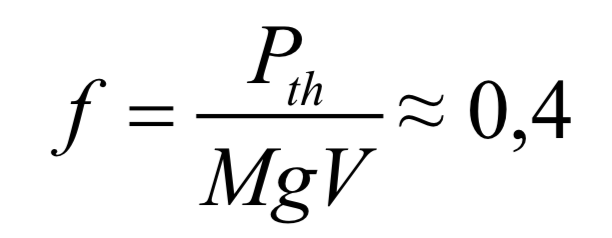En cas de surchauffe il faut évacuer !

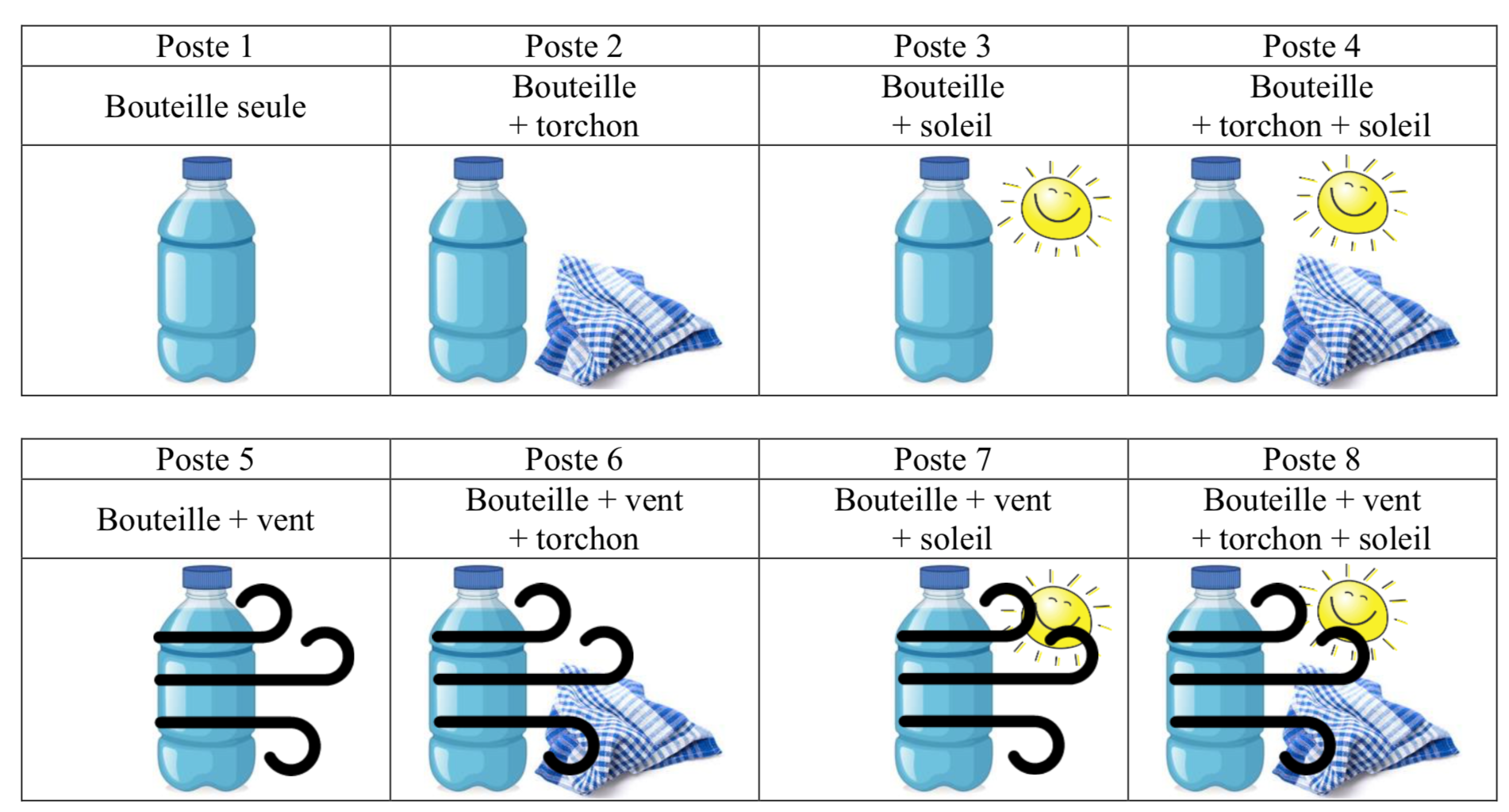
Nous allons chercher à comparer la température de l’eau dans une bouteille dans plusieurs situations : enveloppée ou non d’un torchon mouillé, placée ou non au soleil (en fait sous une lampe à incandescence !), placée ou non dans un courant d’air (créé par un ventilateur).

L’expérience, présentée figure 1, comporte 8 postes avec des bouteilles d’eau identiques (33 cL), à la température ambiance (22°C). On mouille les torchons avec de l’eau à température ambiante (on verse environ 15 cL d’eau sur chaque torchon), on déclenche un chronomètre pour chaque poste et on mesure la température de l’eau au cours du temps, sans oublier d’agiter régulièrement les bouteilles pour uniformiser la température de l’eau.

Figure 1.  Présentation des différentes situations pour comparer la température de l'eau

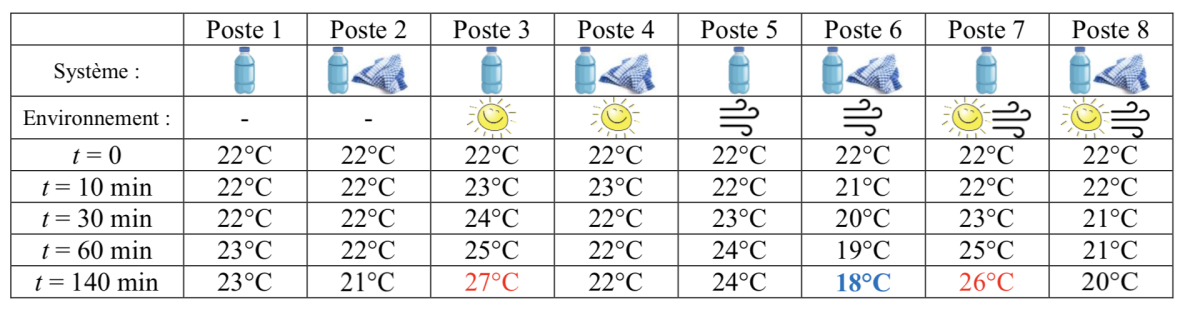
Les résultats obtenus sont regroupés dans le tableau ci-dessous, figure2.

Ces résultats sont principalement figuratifs et une différence de 2°C est difficilement significative. Mais nous allons nous appuyer sur cette première expérience pour approfondir les effets de l'évaporation de l'eau.

Figure 2.  Résultats expérimentaux pour les différentes situations

Remarques

Figure 3.  Image des bouteilles 1, 3 et 6 à la caméra thermique après 140 min

Conclusion

Le moyen le plus efficace de refroidir l’eau dans la bouteille est effectivement de l’envelopper d’un torchon mouillé et de placer l’ensemble dans un courant d’air. Si la bouteille est au soleil, cela marche aussi mais le refroidissement est moindre. Cette méthode est utilisée par les ouvriers du bâtiment qui doivent travailler sur des chantiers extérieurs en été pour refroidir leur bouteille d’eau.

L’évaporation de l’eau dans le torchon, favorisée par le courant d’air, nécessite en fait de l’énergie thermique. Celle-ci est prélevée à l’eau dans la bouteille qui voit sa température diminuer. Peut-on prévoir la quantité d’énergie prélevée par cette évaporation ? Le système peut-il être utilisé dans d’autres situations ?

La température de l’eau dans la bouteille est une mesure de son énergie interne. L’évaporation de la masse $m_{\mathrm{vap}}$ d’eau dans le torchon va prélever l’énergie $m_{\mathrm{vap}}{l}_{\mathrm{vap}}$ où $l_{\mathrm{vap}}$ est la chaleur latente massique de vaporisation de l’eau à la température de l’expérience.

La conservation de l’énergie permet ainsi d’écrire, pour la masse $m_{\mathrm{eau}}$ d’eau dans la bouteille qui passe de la température $T_i$ = 22°C à la température $T_f$ = 18°C :

Où $c_{\mathrm{eau}}$ est la capacité thermique massique de l’eau. On rappelle : $c_{\mathrm{eau}}$ = 4,18.10³ J.kg^-1.K^-1 et $l_{\mathrm{vap}}$ = 2,4.10⁶ J.kg^-1 à pression atmosphérique.

On en déduit la masse d’eau qui s’est évaporée (en négligeant toute perte thermique) :

Remarque : ici on considère le rendement idéal. Nous n'avons pas tenu compte de l'énergie perdue pour refroidir l'air à proximité du torchon mouillé.

Dans l'expérience précédente, la quantité d’eau évaporée représentait environ 1,5% de la masse d’eau contenue initialement dans le torchon. Le processus de vaporisation de l’eau est donc particulièrement efficace pour prélever de l’énergie au système sous forme thermique. Ce principe est utilisé dans les dissipateurs à caloducs.

Nous proposons maintenant, de la même manière, 4 postes pour étudier les effets de l'utilisation de caloducs, figures 5 et 6.

Notons que les quatre calorimètres sont placés dans le courant d’air créé par un ventilateur afin de minimiser toute perturbation due à des mouvements d’air extérieur. La mesure de la température se fait par l’intermédiaire de thermocouples reliés à une interface d’acquisition informatisée.

Figure 5.  Photo des quatre vases de Dewar dans différentes configurations De gauche à droite : Vase de Dewar seul – Vase de Dewar avec 2 tubes vides – Vase de Dewar avec 2 et 4 caloducs.

Figure 6.  Les postes 2 à 4 avec l’interface d’acquisition

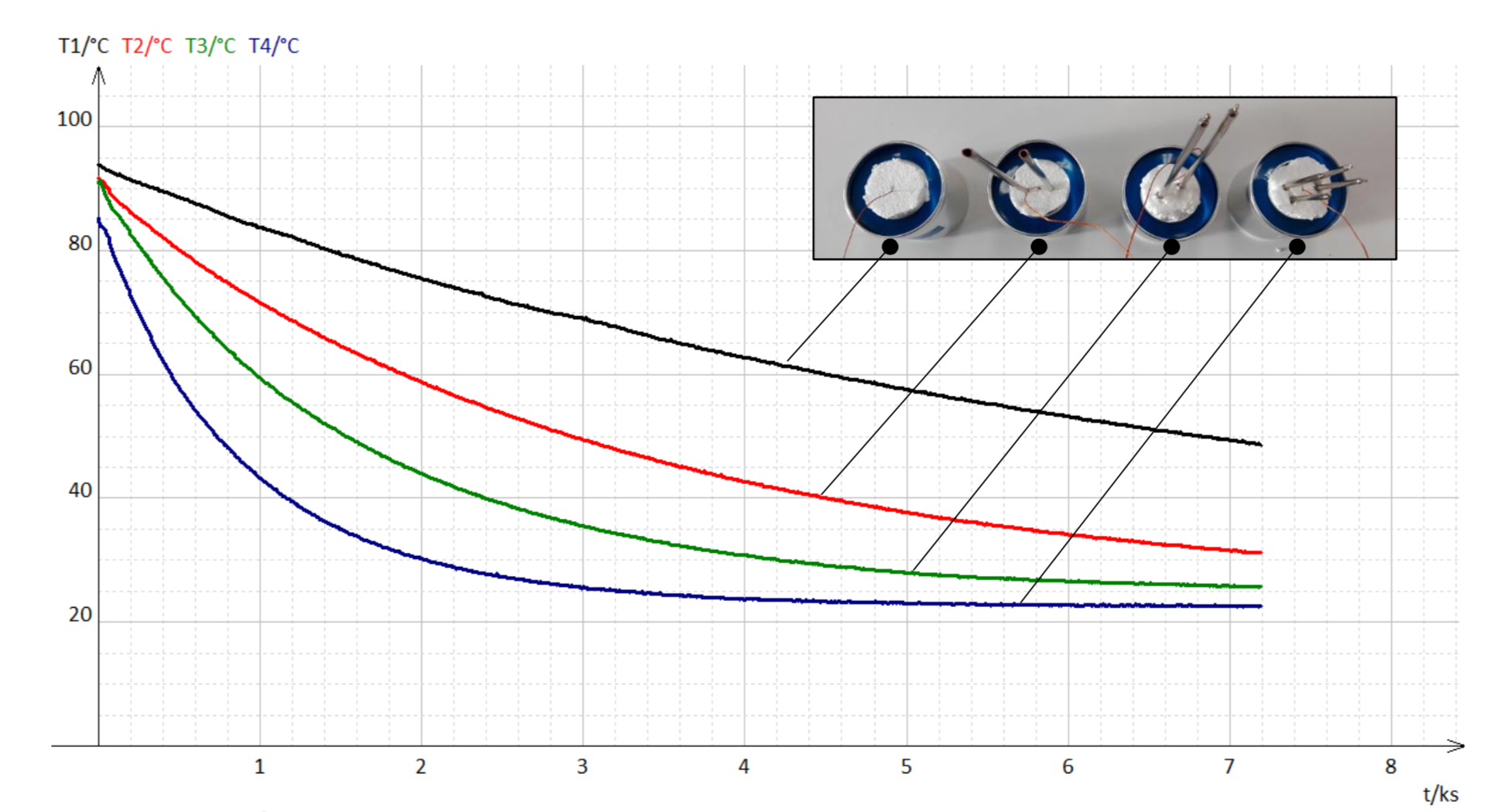
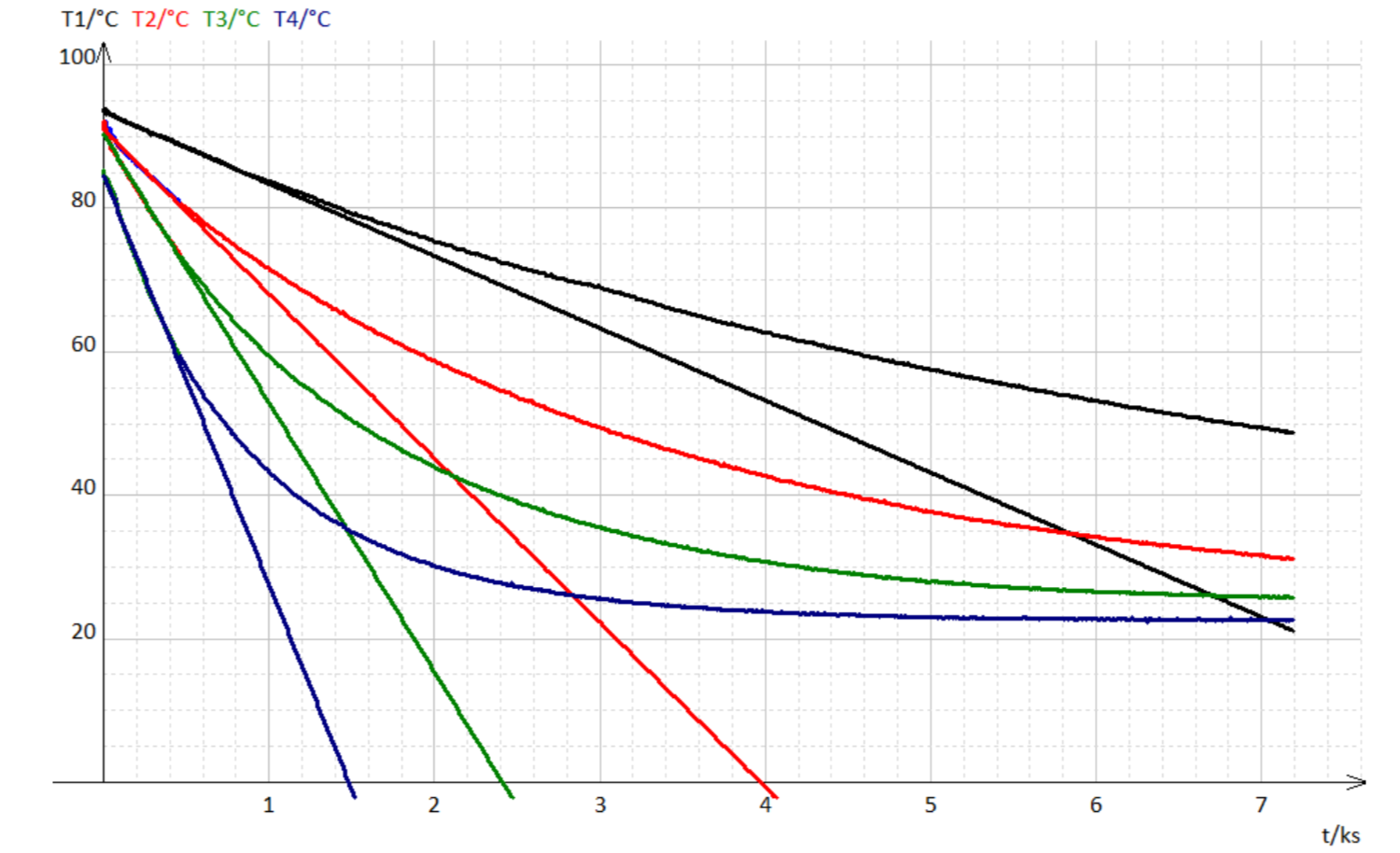
Les mesures de température au cours du temps sont reportées sur le graphe, figure 7.

Figure 7.  Évolution de la température de l’eau dans les vases de Dewar au cours du temps. Attention, l'échelle est donnée en kilosecondes

T1 : Vase de Deware seul – T2 : Vase de Deware avec radiateurs – T3 : Vase de Deware avec 2 caloducs – T4 : Vase de Deware avec 4 caloducs

Les températures initiales sont de l’ordre de 90°C, légèrement différentes d’un vase de Deware à l’autre, le temps de préparer chaque poste avant l’acquisition. Les températures diminuent toutes au cours du temps pour se rapprocher de la température ambiante pour laquelle il y aurait équilibre thermique.

On constate tout d’abord que le vase de Deware seul (poste 1) n’est pas tout à fait calorifugé car la température décroît de manière significative au cours des deux heures d’acquisition. La température du poste 2 décroît plus rapidement grâce à l’effet des dissipateurs thermiques jouant le rôle de radiateur. La température du poste 3 et celle du poste 4 diminuent cependant encore plus rapidement, permettant un refroidissement très efficace de l’eau du vase de Deware. L’effet des caloducs est donc très notable.

Est-il possible de caractériser la puissance thermique perdue dans chaque cas ?

On considère le système constitué par la masse $m_{\mathrm{eau}}$ d’eau dans le vase de Deware et on note $P_{\mathrm{th}}$ la puissance thermique dissipée à l’extérieur. En l’absence de tout chauffage, l’énergie thermique ainsi libérée est directement prélevée sur l’énergie de l’eau, contribuant à diminuer sa température. La conservation de l’énergie entre les instants proches $t$ et $t+dt$ s’écrit alors :

ce qui permet d’écrire :

La puissance dissipée par le système peut ainsi être obtenue directement grâce à la pente de la courbe T(t), figure 8. On mesure graphiquement la pente à l’origine de chaque courbe pour comparer les puissances dissipées en début d’expérience.

Figure 8.  Tracé des tangentes à l’origine de l'évolution de la température de l’eau dans les vases de Deware au cours du temps

On mesure ainsi, pour chaque expérience :

En prenant $m_{\mathrm{eau}}$ = 150.10^-3 kg et $c_{\mathrm{eau}}$ = 4,2.10³ J.kg^-1 (valeur tabulée), on obtient les puissances dissipées :

La puissance dissipée est ainsi plus importante avec l’effet caloduc. On peut d’ailleurs quantifier chaque effet :

La puissance thermique dissipée par les caloducs est loin d’être négligeable : chaque caloduc dissipe en moyenne 8 W de puissance thermique, dont 50% est dû à l’effet radiateur et 50% à l’effet caloduc. Enfin, la puissance thermique dissipée dépend de la température du système : elle est d’autant plus faible que l’écart de température avec l’extérieur diminue. Après un temps assez long, on aurait des puissances thermiques dissipées nulles, indiquant que l’équilibre thermique est atteint.

Il manquerait une expérience témoin. Car dans un premier temps, dans le vase, on ajoute un caloduc qui n’est pas à la température de l’eau (100°C), mais à température ambiante.

On se propose ici de déterminer l’influence de capacité thermique et de la conductivité thermique du caloduc dans l’expérience sur la mesure de la température de l’eau avec effet radiateur.

Les caloducs utilisés sont en cuivre (nickelé extérieurement) et mesurent 250 mm de long avec un diamètre extérieur de 6 mm et un diamètre intérieur de 0,3 mm.

Les tubes ont alors une masse volumique ρ = 8,96.103 kg.m^-3, une capacité thermique massique c = 380 J.kg^-1.K^-1 et une conductivité thermique λ = 401 W.m^-1.K^-1.

En notant r₁ et r₂ les rayons intérieur et extérieur du tube respectivement et H la longueur du caloduc, le volume de métal dans le tube s’écrit :

D'où la masse du tube :

On en déduit la masse totale d’un tube de cuivre : m = 12.10^-3 kg

Cette masse n’a pas été mesurée directement, mais l’ordre de grandeur semble tout à fait cohérent.

On étudie le réchauffement du tube de la température ambiante 20°C à la température de travail initiale 100°C. D’après le premier principe appliqué au système supposé isolé {tube + eau dans le calorimètre} pendant cette étape :

L’eau qui se refroidit réchauffe le tube. La variation de température de l’eau vaut :

Avec m_eau = 150.10^-3 kg dans le calorimètre, on obtient ΔT_eau = -0,6 K

Cette variation de température semble plutôt faible par rapport aux températures mesurées. Evaluons à présent la puissance thermique prélevée à l’eau pendant le réchauffement du tube. Le temps caractéristique de diffusion thermique dans le tube s’exprime en outre par :

où L est une taille caractéristique de la diffusion dans le tube.

La diffusion se fait principalement radialement pour la partie immergée. Avec L = 3 mm, on obtient : τ = 0,08 s

Le temps de diffusion radiale est même en réalité beaucoup plus petit puisqu’il s’agit seulement de réchauffer le tube sur une épaisseur de 0,3 mm.

Si on considère la conduction thermique le long du tube extérieur avec L = 200 mm (longueur émergée du tube), on obtient cette fois : τ = 3,3.10² s

En combinant ce temps caractéristique avec la variation de température de l’eau dans le calorimètre, on aboutit à une pente :

soit encore, pour deux caloducs plongés dans l’eau (comme dans l’expérience présentée) :

ce qui correspond à une puissance thermique prélevée à l’eau pendant la phase de réchauffement du tube :

Cette puissance représente environ 30% de la puissance mesurée (7,7 W) et attribuée à l’effet radiateur.

Conclusion

La prise en compte du réchauffement du tube permet d’affiner la mesure de la puissance thermique dissipée par effet radiateur dans les caloducs et de mieux interpréter les mesures. L’effet n’est pas énorme sans toutefois être complètement négligeable. Un modèle plus complet devra envisager les différents phénomènes au cours du temps afin de pouvoir quantifier précisément leurs effets respectifs. Cependant, l’influence du réchauffement des tubes devient négligeable lorsque l’on étudie la vaporisation de l’eau dans le tube qui prélève une puissance thermique bien plus élevée.

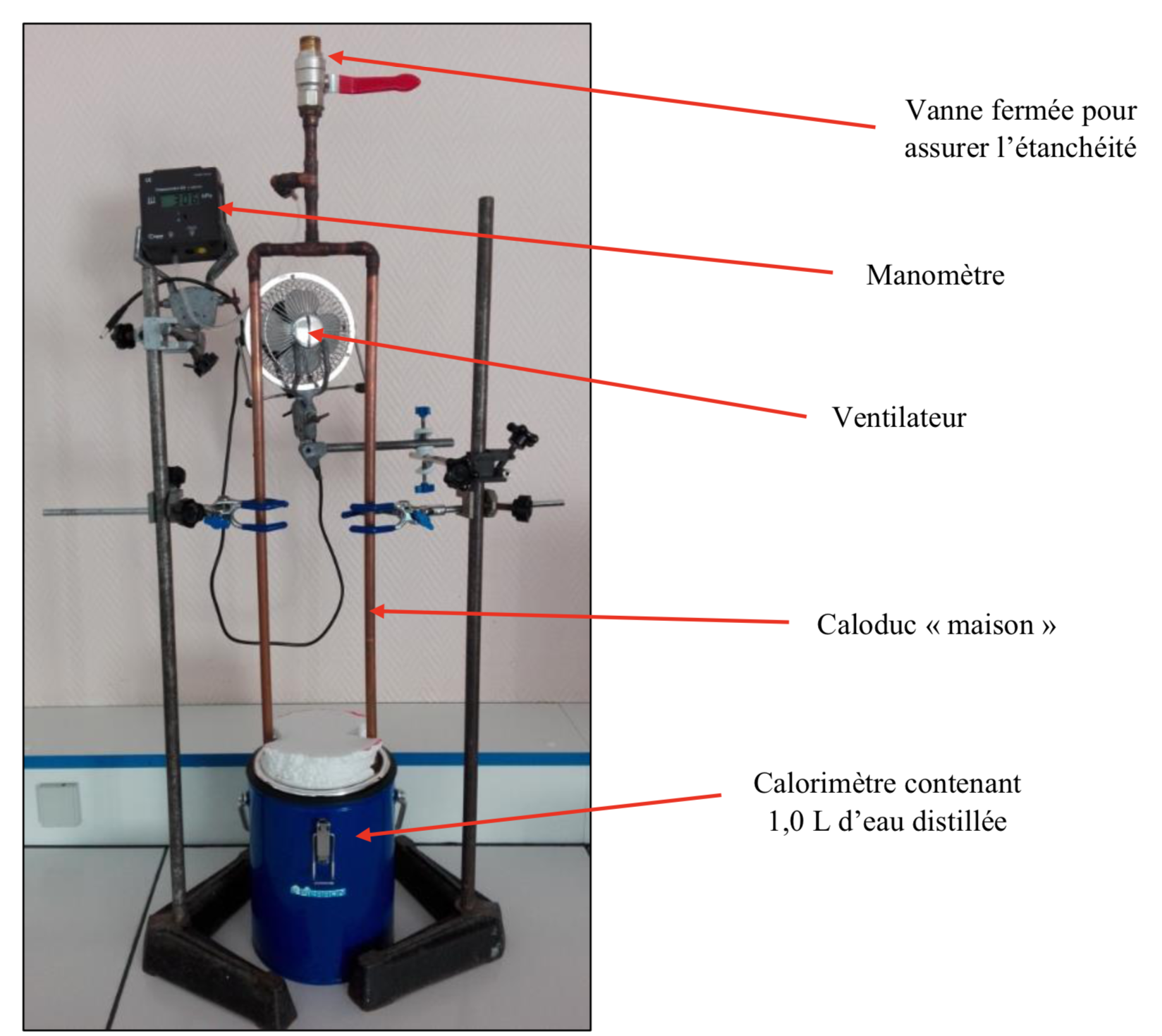
Notre caloduc « maison » est fabriqué avec des tuyaux de cuivre soudés de diamètre intérieur 10 mm. Ses dimensions ont été choisies pour s’adapter parfaitement aux calorimètres du laboratoire. Une vanne permet d’assurer une étanchéité parfaite du système lorsque celle-ci est fermée. Un manomètre permet de contrôler la pression qui règne à l’intérieur des tuyaux, figure 9.

Figure 9.  Caloduc « maison »

Lorsque les tubes sont vides d’eau, le système sert de dissipateur thermique par effet radiateur : l’énergie thermique est alors prélevée par simple conduction thermique dans le cuivre pour être transférée à l’extérieur (dans l’air ambiant).

Pour être utilisé comme caloduc, le dispositif nécessite un peu de préparation :

On verse dans le tube 90 mL d’eau distillée par la vanne ouverte. On met ensuite la base à chauffer pour faire bouillir l’eau à l’intérieur pendant 45 minutes, la vanne restant ouverte. Nous avons utilisé un système de chauffage des tubes de verre utilisé au laboratoire de chimie. La vapeur d’eau créée pendant cette ébullition permet ainsi de chasser l’air des tuyaux. Enfin, on ferme la vanne, on éteint le chauffage et on laisse le système se refroidir. On constatera (à la fin des expériences) qu’il reste alors 35 mL d’eau dans le tube. Il reste donc essentiellement de l'eau liquide en équilibre avec de la vapeur d'eau.

Lorsque le dispositif est à température ambiante, on remarque que la pression dans le tube atteint 55 hPa, soit une pression presque 20 fois inférieure à la pression atmosphérique ! Il règne donc un vide partiel dans notre système... C’est le principe de l’expérience du Bouillant de Franklin [3].

On reprend le principe des expériences faites avec les caloducs commerciaux.

On place 1,0 L d’eau bouillante dans un calorimètre et on mesure l’évolution de la température de l’eau au cours du temps grâce à une acquisition informatique, figure 10. On refait l’expérience dans les trois situations suivantes :

Figure 10.  L’expérience consiste à plonger le caloduc « maison » dans le calorimètre et à mesurer l’évolution de la température de l’eau au cours du temps. Le capteur de température (non représenté ici) est relié à une carte d’acquisition informatique

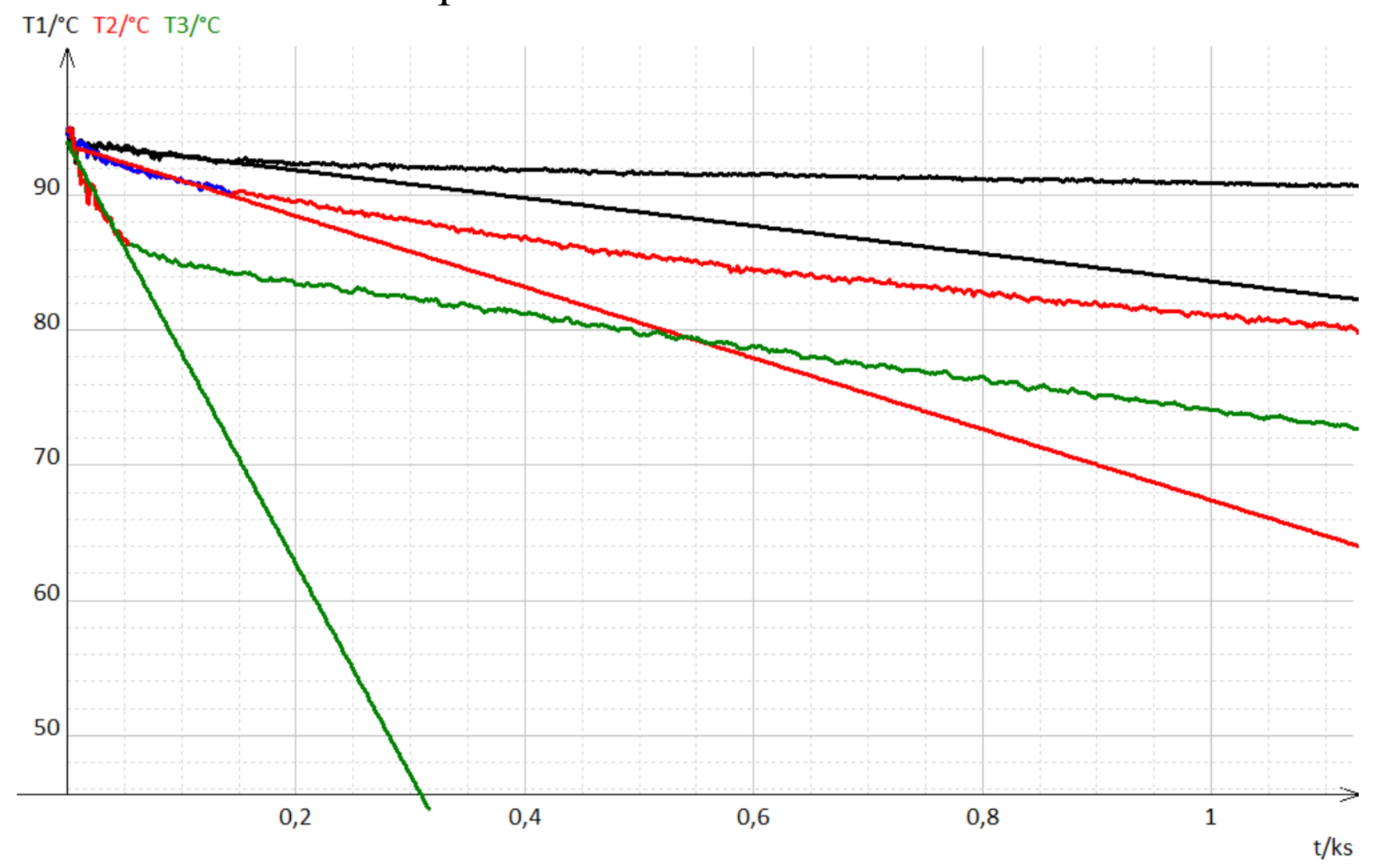
Les mesures de température au cours du temps pour les trois expériences sont reportées sur le graphe, figure 11.

Figure 11.  Évolution de la température de l’eau dans le calorimètre au cours du temps

Courbe 1 (noir) : Calorimètre seul -  Courbe 2 (rouge) : Calorimètre + caloduc à tubes vides -  Courbe 3 (vert) : Calorimètre + caloduc « maison ».

L’eau se refroidit lentement dans le calorimètre seul, indiquant une bonne isolation thermique. Le refroidissement est plus rapide avec le dissipateur à tubes vides et encore plus rapide avec le caloduc « maison », ce qui confirme à nouveau l’efficacité de l’effet caloduc dans le tube, comme cela avait été déjà constaté avec les caloducs commerciaux.

On remarque cependant que l’évolution de la température avec le caloduc est extrêmement rapide uniquement pendant les 60 premières secondes de l’expérience. Ensuite, l'évolution suit le même rythme que dans l'expérience avec le caloduc à tubes vides.

On mesure graphiquement la pente des tangentes à chaque courbe au début de l’expérience :

On note, tout de même que la mesure de la pente de la tangente de la courbe 2 reste approximative et permet de donner une idée qualitative des pertes thermiques par effet radiateur et prélevée à l’eau pendant la phase de réchauffement du tube.

On en déduit la puissance thermique dissipée dans chaque cas par la relation :

Où $m_{\mathrm{eau}}$ = 1,0 kg et $c_{\mathrm{eau}}$ = 4,2.10³ J.kg^-1, on trouve :

Les pertes thermiques par le calorimètre valent ainsi :

L’effet caloduc seul dissipe une puissance thermique presque 8 fois supérieure à celle de l’effet radiateur ! Notre caloduc « maison » joue bien son rôle de dissipateur thermique efficace !

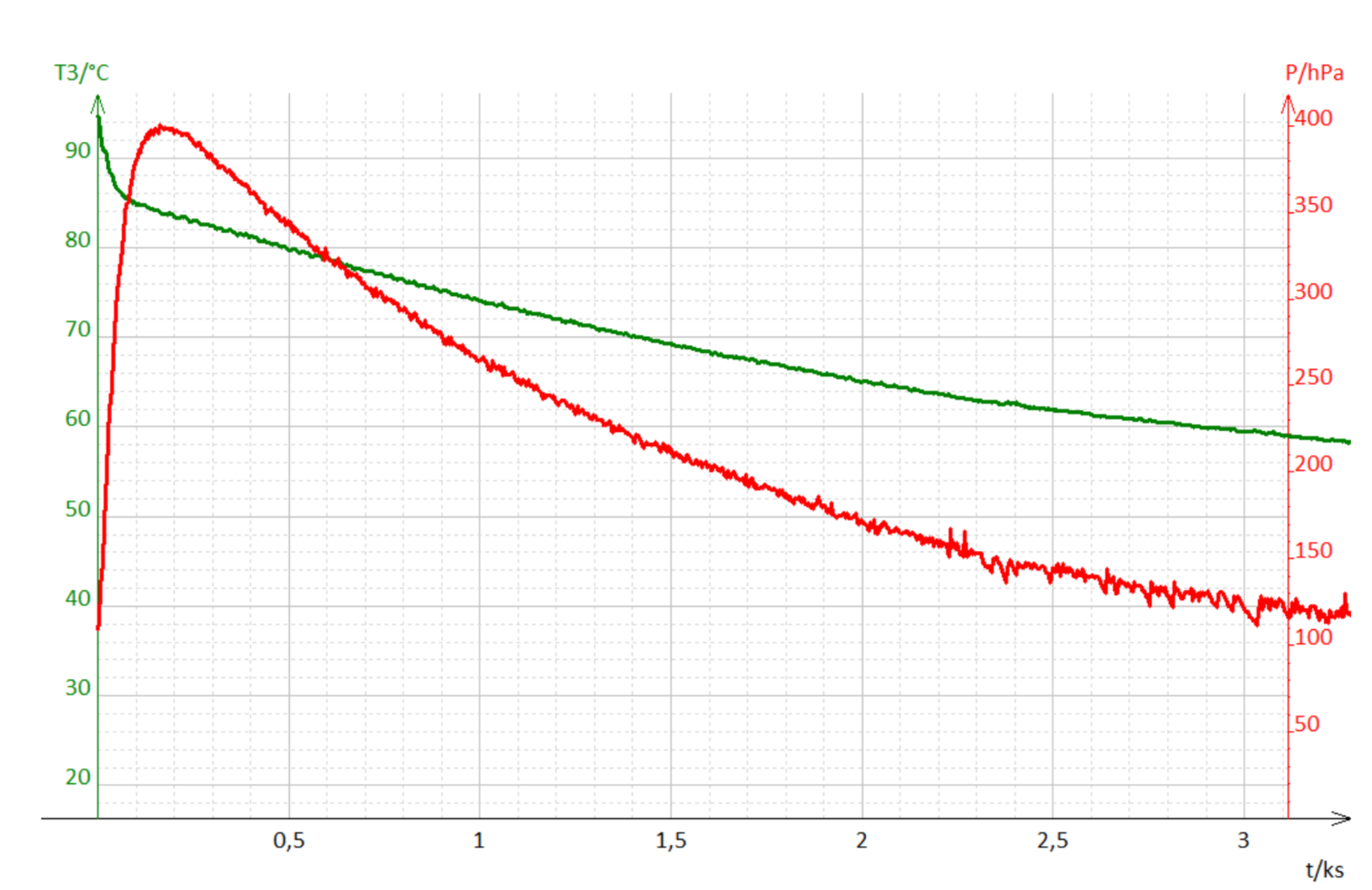
Afin de comprendre les phénomènes mis en jeu, on trace l’évolution de la pression dans le tube au cours du temps, mesurée avec le manomètre, figure 12.

Figure 12.  Évolution de la température (vert) et de la pression (rouge) dans le caloduc « maison » au cours du temps

On constate que la pression dans le tube augmente très rapidement pendant les trois premières minutes de l’expérience, avant de diminuer lentement au cours du temps. Expérimentalement on a même pu observer un « bruit » d’ébullition dans le tube au moment où l’on a versé l’eau bouillante dans le calorimètre... Le tracé de la pression en fonction de la température permet de retrouver simplement le diagramme de phase de l’eau.

L’efficacité de notre caloduc « maison » à thermosiphon est maximale lorsque la température du milieu à refroidir est comprise entre 85°C et 95°C car la vaporisation de l’eau dans le tube est alors la plus efficace. Lorsque la température est plus basse, on retrouve le fonctionnement du dissipateur thermique à effet radiateur. Pour pouvoir utiliser notre caloduc sur des plages de températures plus importantes, il faudrait diminuer encore la pression qui règne dans le tube.

Notre caloduc « maison » à thermosiphon absorbe une puissance thermique $P_{\mathrm{th}}$ = 520 W pendant environ 60 s. Cette puissance est utilisée pour vaporiser l’eau dans le tube et assurer la circulation du fluide.

L’énergie thermique à apporter pour vaporiser une masse $dm$ d’eau pendant la durée $dt$ vaut :

où $l_{\mathrm{vap}}\mathrm{(T)}$ est l’enthalpie masse de vaporisation de l’eau à la température T. On en déduit la masse d’eau vaporisée par unité de temps sous la forme du débit massique :

En prenant $l_{\mathrm{vap}}$ = 2,1.10⁶ J.kg^-1 et $P_{\mathrm{th}}$ = 520 W, on obtient  $D_m$ = 2,5.10^-4 kg.s^-1

En considérant que la vaporisation dure $\mathrm{\Delta t}$ = 60 s, la masse d’eau vaporisée vaut : $m_{\mathrm{vap}}=D_m\mathrm{\Delta t}$ = 15.10^-3 kg, ce qui représente 43% de l’eau présente initialement dans le tube !

Le système de refroidissement à caloduc tient ainsi son efficacité de la vaporisation de l’eau dans le tube qui permet une circulation du fluide et un échange thermique rapide avec le milieu extérieur.

Au début de l’expérience, l’eau dans le calorimètre a une température comprise entre 95°C et 85°C. Cela réchauffe rapidement le tube et l’eau à l’intérieur...qui se met à bouillir ! Cette ébullition de l’eau à une température inférieure à 100°C (température d’ébullition de l’eau sous la pression atmosphérique) est rendue possible car la pression initiale dans le tube est très faible !

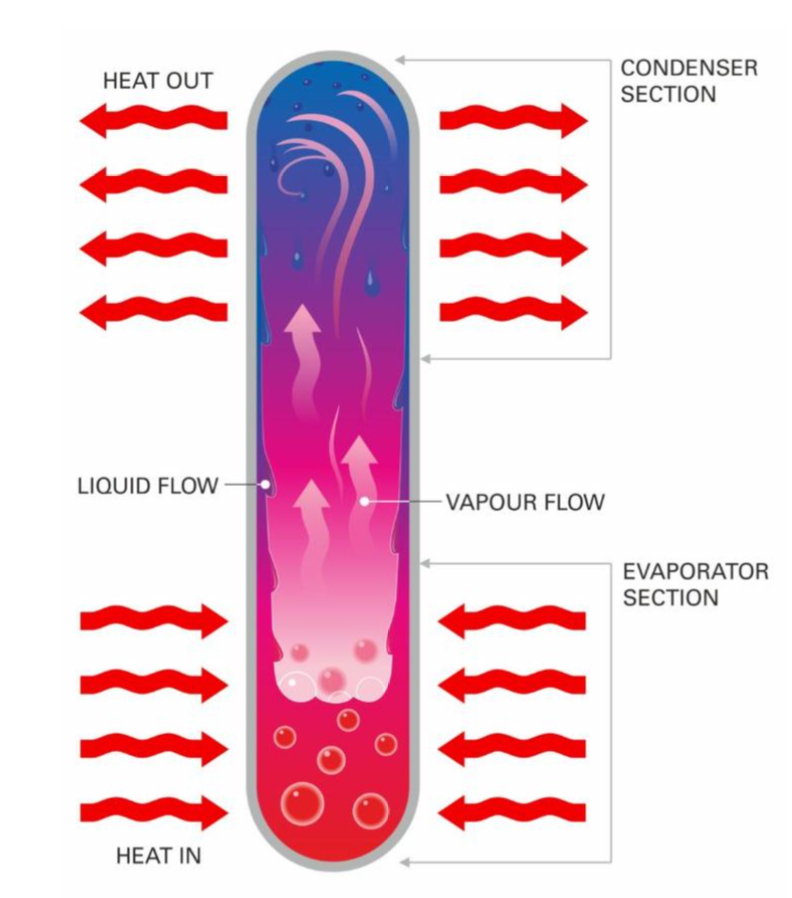
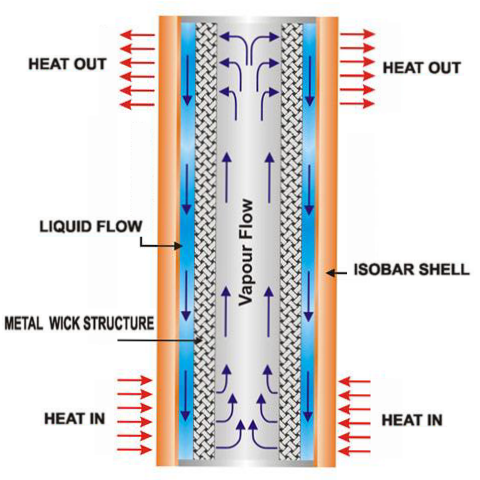
La puissance thermique absorbée par le caloduc permet la transition de phase de l’état liquide à l’état vapeur. La vapeur d’eau monte alors dans le tube, se refroidit à cause du courant d’air créé par le ventilateur, se liquéfie sur les bords intérieurs et retombe pour être à nouveau vaporisée... Notre caloduc « maison » utilise la gravité pour assurer la circulation du fluide à l’intérieur selon le principe des thermosiphons, employés notamment dans les systèmes de chauffage solaire.

Figure 13.  Principe de fonctionnement d'un caloduc gravitaire (source : www.etekina.eu)

Figure 14.  Principe de fonctionnement d'un caloduc capillaire (source : https://www.acrolab.com/isobar-heat-pipes)

Dans le cas du caloduc gravitaire, le liquide (en bas) se vaporise au contact de la source de chaleur en absorbant de l’énergie ; la vapeur ainsi créée monte, se liquéfie en libérant de l’énergie et redescend sous forme liquide par gravité, figure 13.

Un caloduc commercial fonctionne sur le même principe, mais le retour de la vapeur est assuré par capillarité dans une structure de mailles (wick) ou des poudres métalliques très fines. Un tel système peut être utilisé en principe dans tous les sens, figure 14.

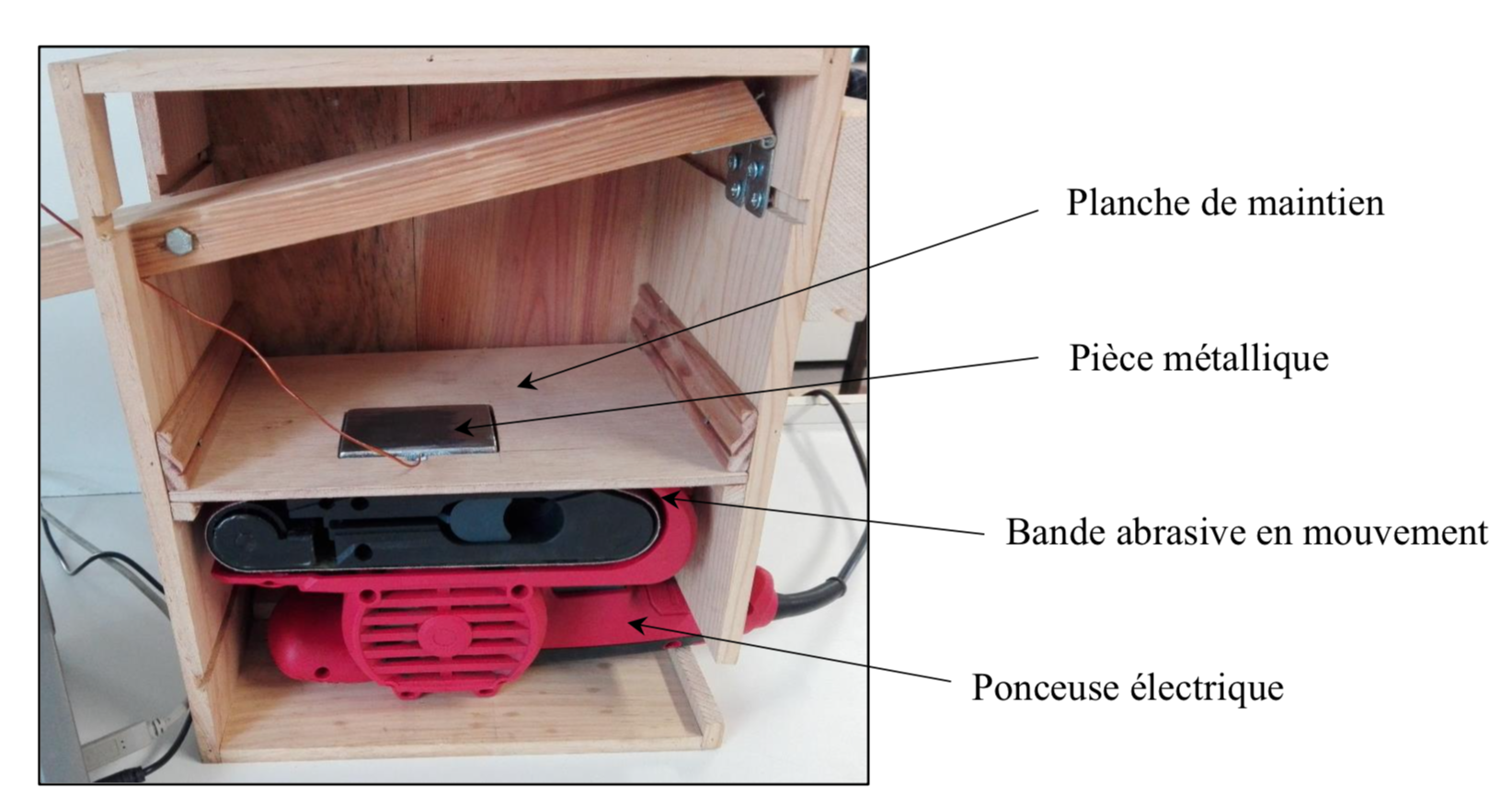
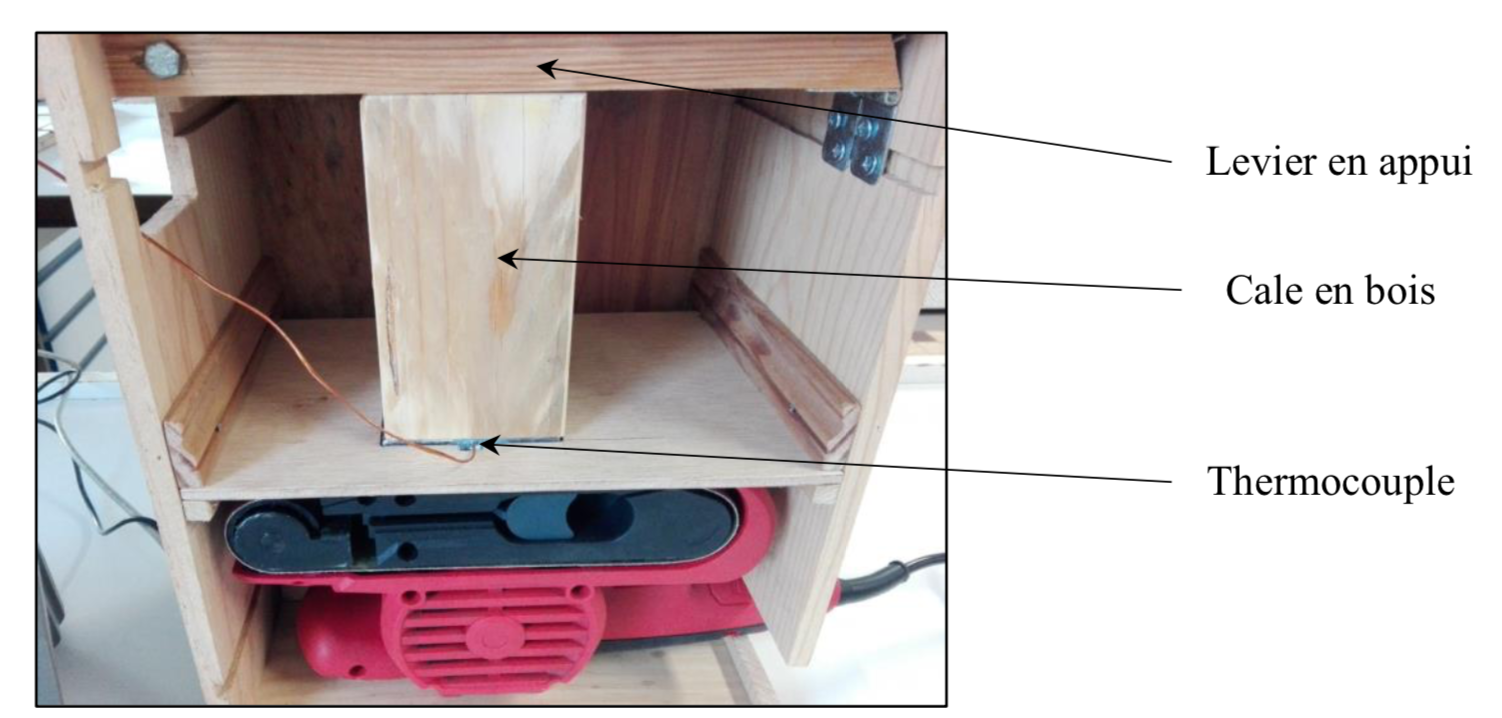
On se propose de modéliser expérimentalement le système de freinage d’un train à grande vitesse en utilisant une pièce en acier en appui sur une ponceuse à bande, figure 15.

Figure 15.  Dispositif expérimental de freinage d'une ponceuse

La pièce métallique (parallélépipède en acier de dimensions 75 mm x 50 mm x 8 mm et de masse 220 g) est maintenue en appui sur la bande de la ponceuse par un levier et une cale en bois. On place des masses marquées à l’extrémité du levier pour exercer une force connue sur la pièce métallique. Un thermocouple placé dans l’épaisseur de la pièce et relié à une interface d’acquisition informatique permet de mesurer la température au cours du temps. La ponceuse est reliée à la prise électrique par l’intermédiaire d’un alternostat permettant d’imposer la tension d’alimentation et de régler ainsi la vitesse de la bande.

Étalonnage de la vitesse de déplacement de la bande

Afin de connaître la vitesse de déplacement de la bande, nous avons tout d’abord réalisé un étalonnage du montage.

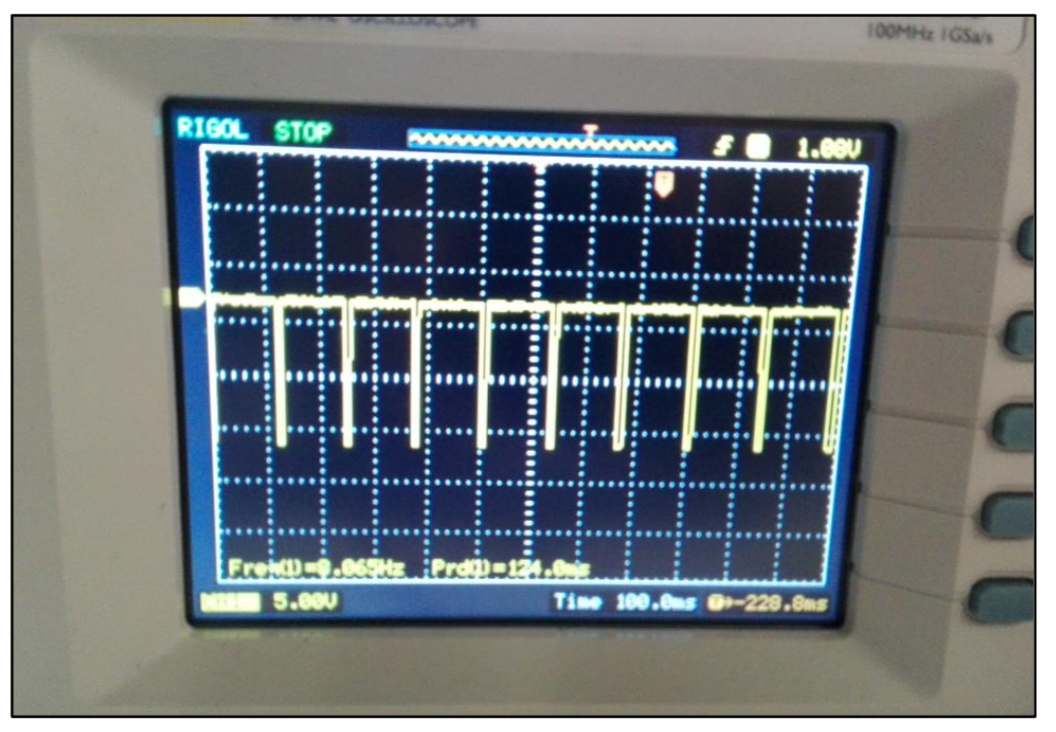
Un disque est mis en rotation par le contact avec la bande. On mesure sa vitesse de rotation en déterminant la fréquence de clignotement d’un faisceau laser passant par deux trous du disque, figure 16. Le faisceau laser est en effet envoyé sur un montage à photodiode relié à un oscilloscope numérique, figure 17.

Figure 16.  Montage d’étalonnage de la vitesse de la bande

Figure 17.  Capture d’écran de l’oscilloscope numérique avec le signal délivré par la photodiode

On note f_laser la fréquence de clignotement du laser. Puisque le disque comporte deux trous, la fréquence de clignotement est deux fois plus grande que la fréquence de rotation. La vitesse de rotation Ω du disque vaut alors simplement Ω = π f_laser.

La vitesse V de la bande s’obtient ainsi par la relation : V = R Ω = π f_laser où R = 14,9 cm est le rayon du disque utilisé.

Par exemple, pour une fréquence f_laser = 8,0 Hz (figure 17), on obtient : V = 3,7 m/s.

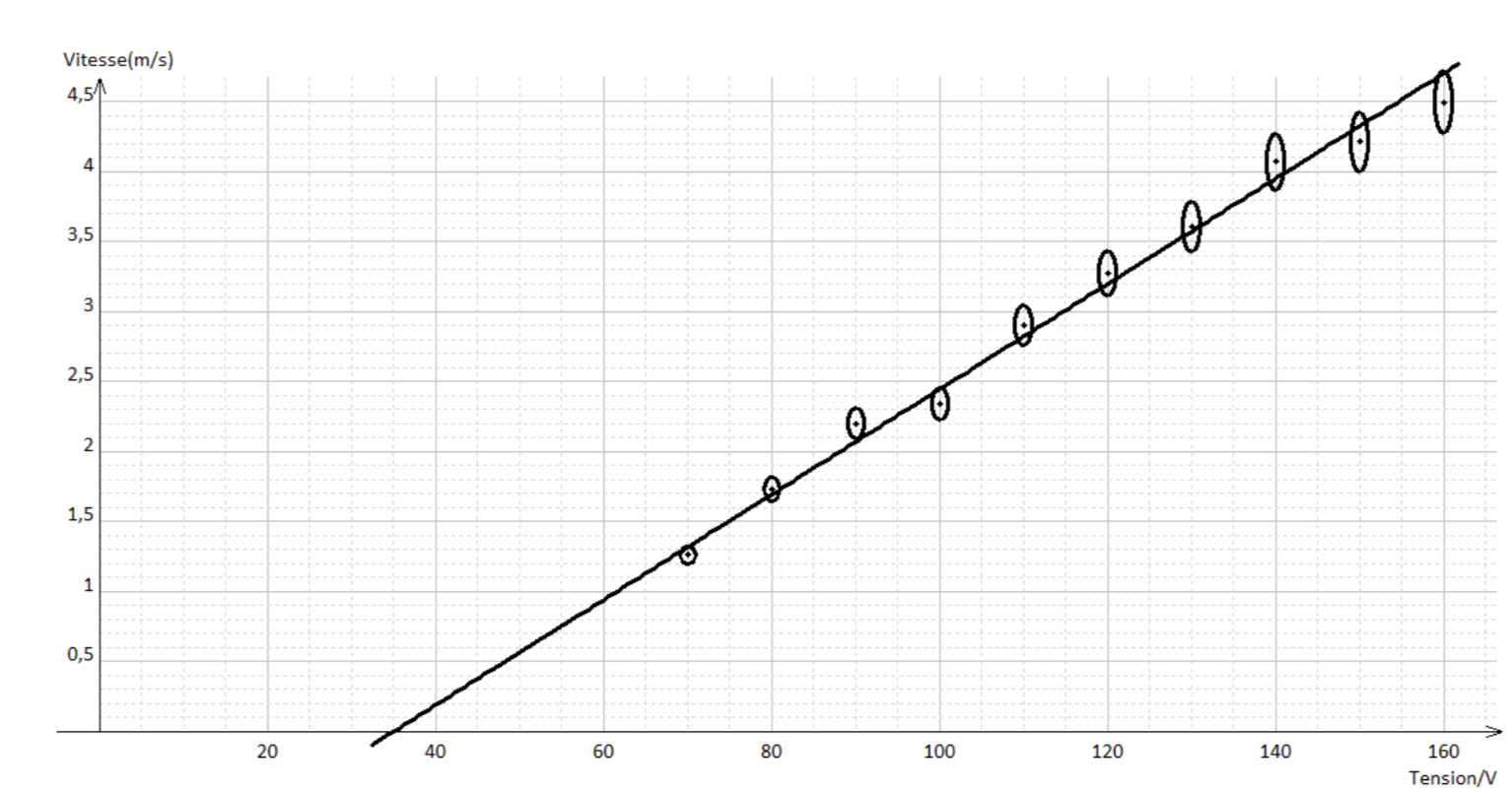
On mesure ainsi la vitesse de translation de la bande en fonction de la tension d’alimentation, figure 18. Notons que nous avons limité la tension d’alimentation à 160 V pour cet étalonnage, car au-delà le disque tournait vraiment très vite et cela pouvait devenir dangereux...

Figure 18.  Vitesse de translation de la bande en fonction de la tension d’alimentation

On peut considérer une relation affine entre la vitesse V et la tension d’alimentation u : V(m.s^-1) = −1,3 + 0,038 u (V)

En extrapolant cette relation à tout le domaine d’utilisation de la ponceuse, on peut déterminer la vitesse maximale de la bande, obtenue pour u = 240 V : V_max = 7,8 m/s (soit 28 km/h).

À l’aide du levier, on appuie sur la plaque (avec un total de 650 g de masses marquées à l’extrémité) pour augmenter le frottement sur la bande. La masse équivalente de la pièce métallique sur la bande vaut alors 3,9 kg (mesuré avec une balance placée à la place de la ponceuse). On mesure alors expérimentalement la température de la plaque d’acier au cours du temps lorsque l’on allume la ponceuse.

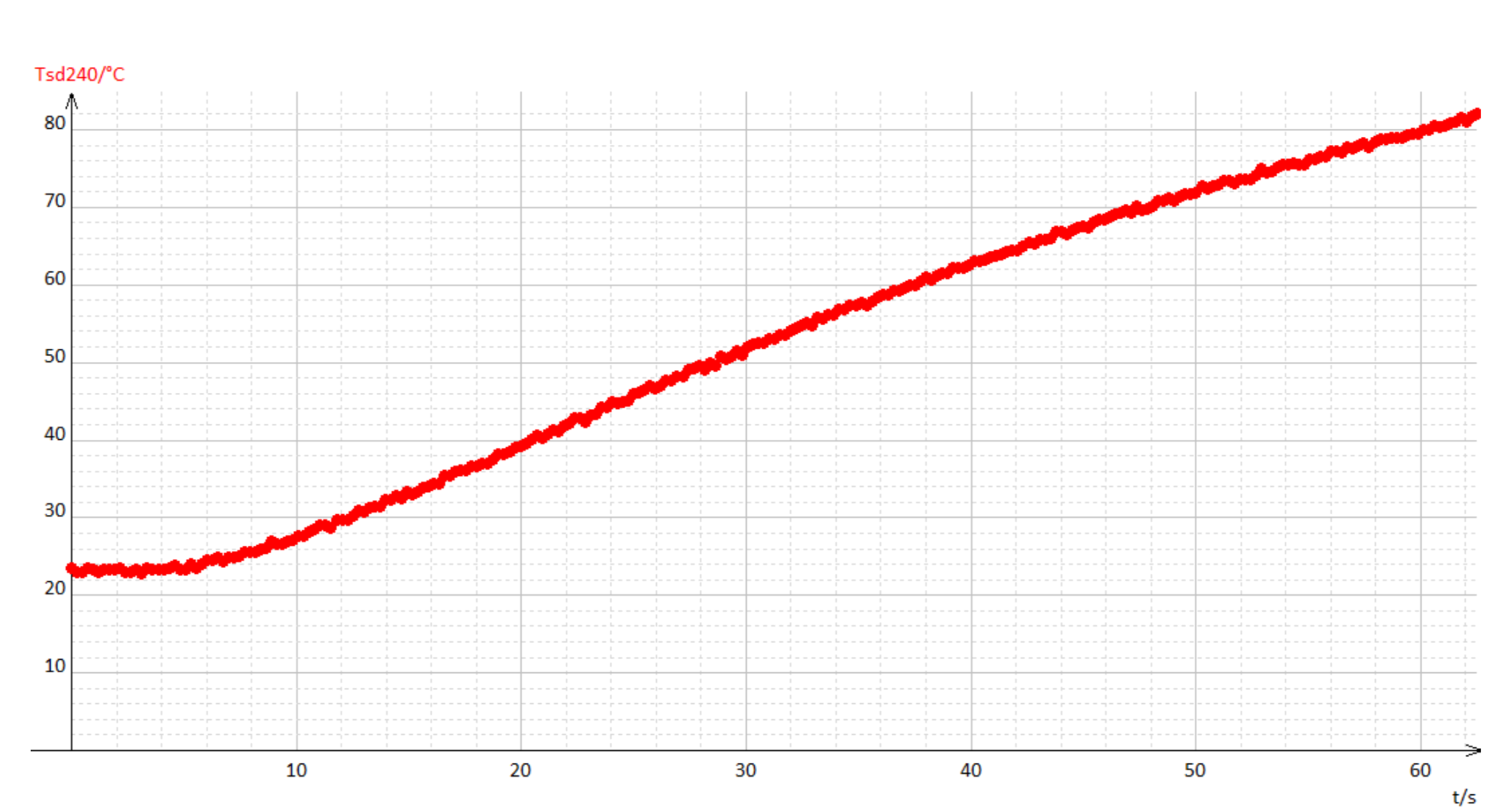
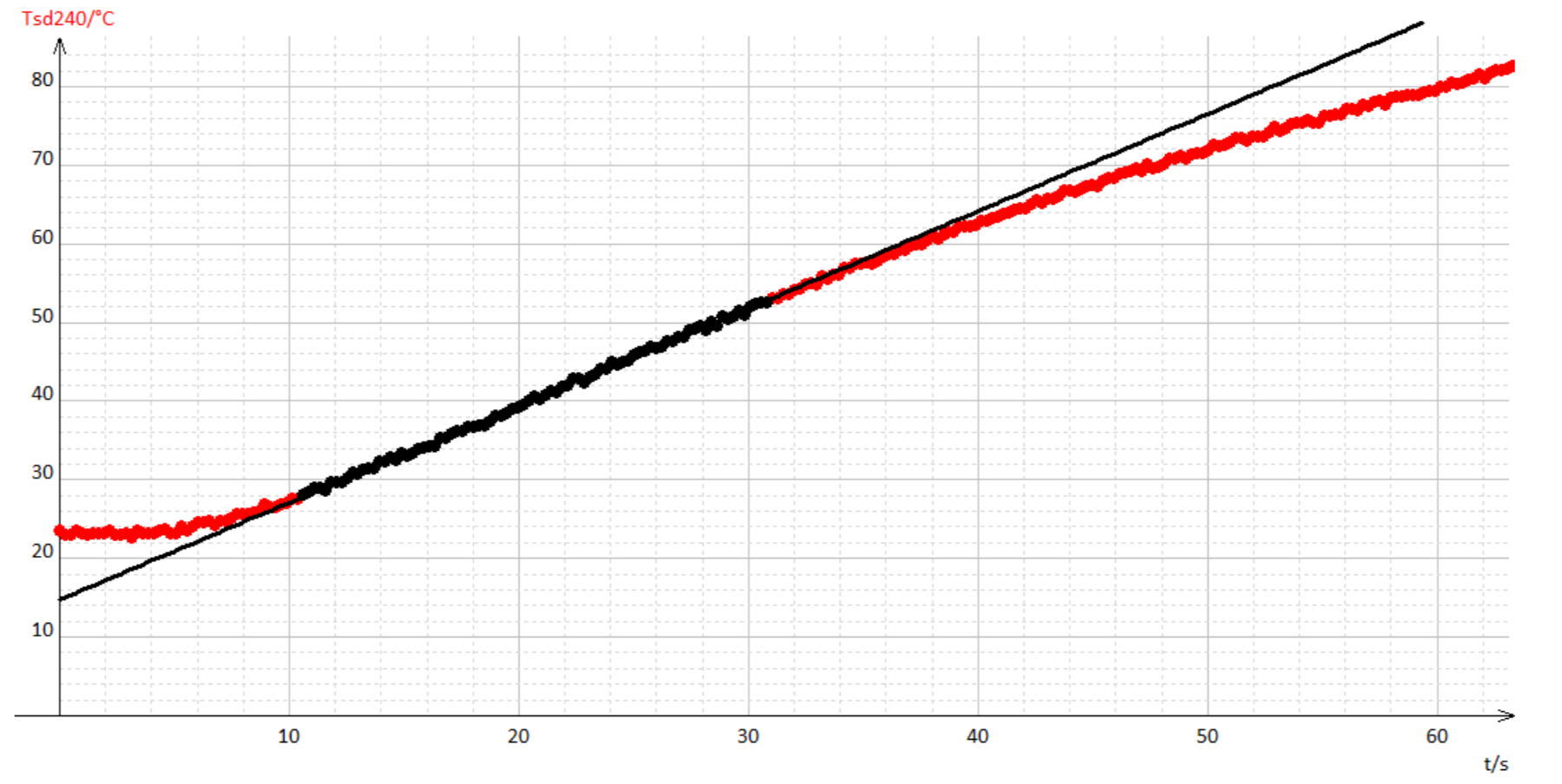
La courbe de température obtenue pour une tension d’alimentation de 240 V est reportée figure 19.

Figure 19.  Température de la plaque métallique au cours du temps. Tension d’alimentation 240 V – Vitesse de la bande 7,8 m.s-1

On observe que la température de la plaque en acier augmente au cours du temps, du fait des frottements sur la bande, modélisant le freinage. Cependant, la montée en température n’apparaît que quelques secondes après le démarrage de la ponceuse, le temps que l’énergie thermique diffuse de proche en proche dans l’épaisseur de la plaque.

Comme cela a déjà été fait précédemment, on peut relier la pente de la courbe T(t) à la puissance thermique apportée à la plaque par le chauffage :

On mesure la pente graphiquement, figure 20.

Figure 20.  Température de la plaque métallique au cours du temps Tension d’alimentation 240 V – Vitesse de la bande 7,8 m.s-1

L’écart au modèle linéaire est relativement faible. Les pertes thermiques sont donc très faibles pendant les premières secondes de chauffe. On mesure ainsi :

Avec m_acier = 2,2.10^-1kg et c_acier = 4,7.10² J.kg^-1.K^-1, on peut calculer la puissance thermique apportée par les frottements avec la bande abrasive :

La force de frottement $F$ qui s’exerce sur la plaque peut s’écrire : $F=fMg$ où $f$ est le coefficient de frottement entre les deux solides, $M$ = 3,9 kg la masse équivalente de la plaque en appui sur la bande et $g$ l’accélération de la pesanteur. En considérant que la puissance de cette force de frottement est entièrement dissipée sous forme thermique (en réalité une partie de cette puissance sert à poncer la plaque !), on obtient la relation :

c’est-à-dire, avec $V$ = 7,8 m.s^-1 :

On retrouve le coefficient de frottement caractéristique entre de l’acier et une garniture de frein [5]. Notre modèle est tout à fait cohérent avec un système de freinage réel !

On constate enfin que sur l’échelle de temps considérée l’évolution de la température est quasiment linéaire avec le temps, ce qui indique que la plaque en acier est pratiquement isolée thermiquement et qu’il n’y a presque pas de pertes thermiques.

Après 60 s, la pièce métallique atteint une température avoisinant 80°C.

Est-il possible de limiter la température atteinte par la pièce métallique en utilisant un dissipateur thermique ?

Nous avons monté un dissipateur thermique commercial à caloducs sur notre pièce métallique afin d’étudier les transferts thermiques dans la nouvelle situation. Il s’agit d’un dispositif de dissipation thermique utilisé dans les ordinateurs, combinant la conduction thermique dans les tubes, l’effet caloduc et la convection imposée par un ventilateur intégré, figure 21.

Figure 21.  Gauche : Dissipateur thermique. Droite : Dissipateur thermique pour ordinateur monté sur la pièce métallique en appui sur la ponceuse

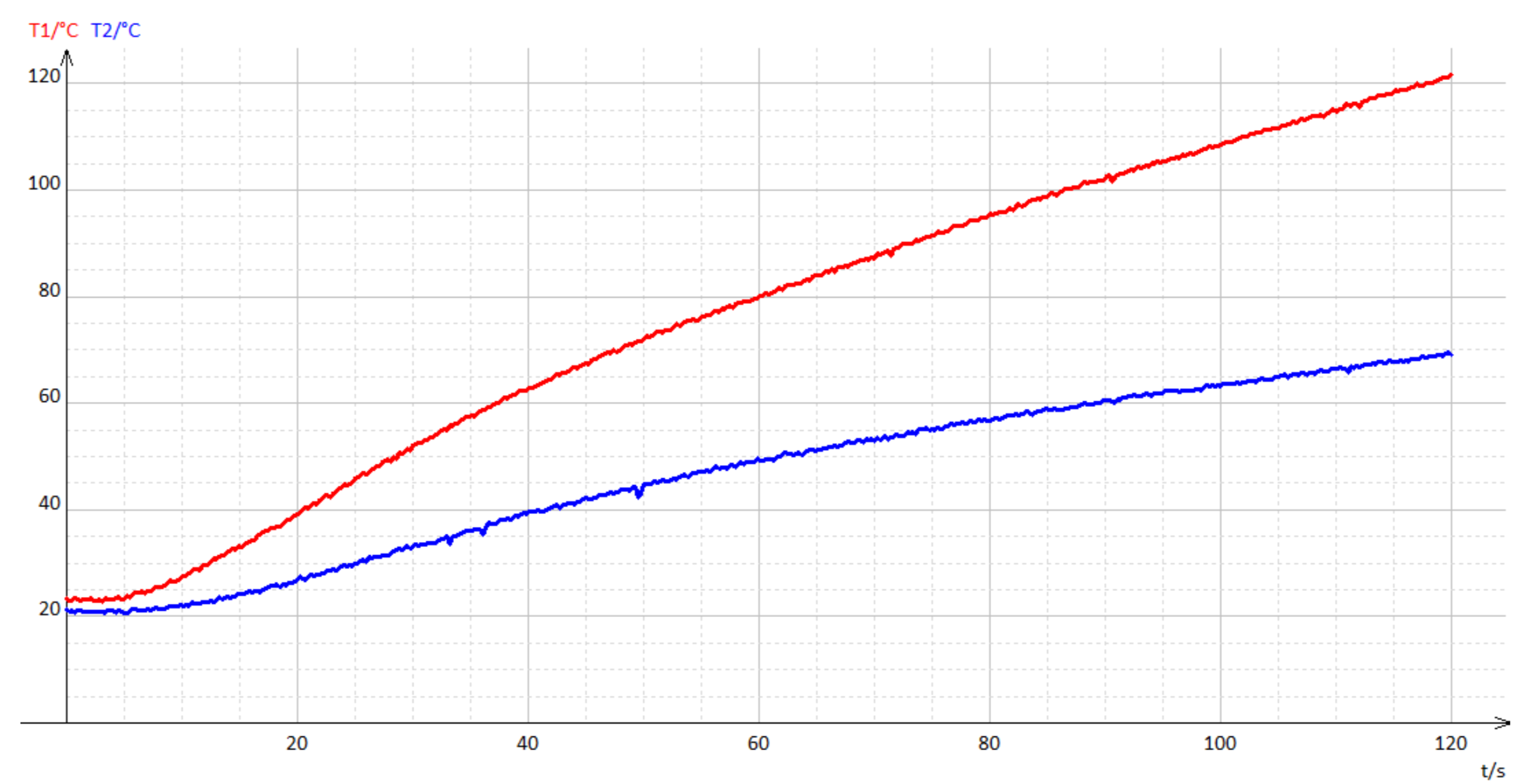
On mesure alors la température de la plaque dans les mêmes conditions que précédemment sur une durée de 120 s, en présence du dissipateur thermique, pour une tension d’alimentation de la ponceuse de 240 V, figure 22.

Figure 22.  Évolution de la température de la plaque

Sans dissipateur thermique (en rouge – T1) ; Avec dissipateur thermique à caloducs (en bleu – T2); Tension d’alimentation 240 V – Vitesse de la bande 7,8 m.s-1.

On constate que la température de la plaque évolue bien plus lentement en présence du dissipateur thermique. La température après 120 s vaut seulement 70°C, contre 120°C sans le dissipateur – on avait même pu vaporiser des gouttelettes d’eau à la surface de la plaque à la fin de l’expérience ! Ce qui montre à nouveau l’efficacité du système de refroidissement à caloducs.

On souhaiterait cependant pouvoir atteindre un régime stationnaire pour lequel la puissance apportée serait complètement dissipée sous forme thermique, la température de la pièce métallique restant constante. Il faut pour cela attendre plus longtemps, ce qui risquerait d’endommager notre ponceuse...

Nous avons donc eu l’idée de placer la pièce métallique directement sur une plaque chauffante, dans trois situations différentes : sans dissipateur (pièce métallique seule), avec dissipateur à caloducs et avec dissipateur modifié (les tubes ont été sciés pour éviter l’effet caloduc et obtenir un radiateur seul), figure 23.

Figure 23.  Pièce métallique sur une plaque chauffante (gauche) avec dissipateur à caloducs (milieu) ou radiateur seul (droite)

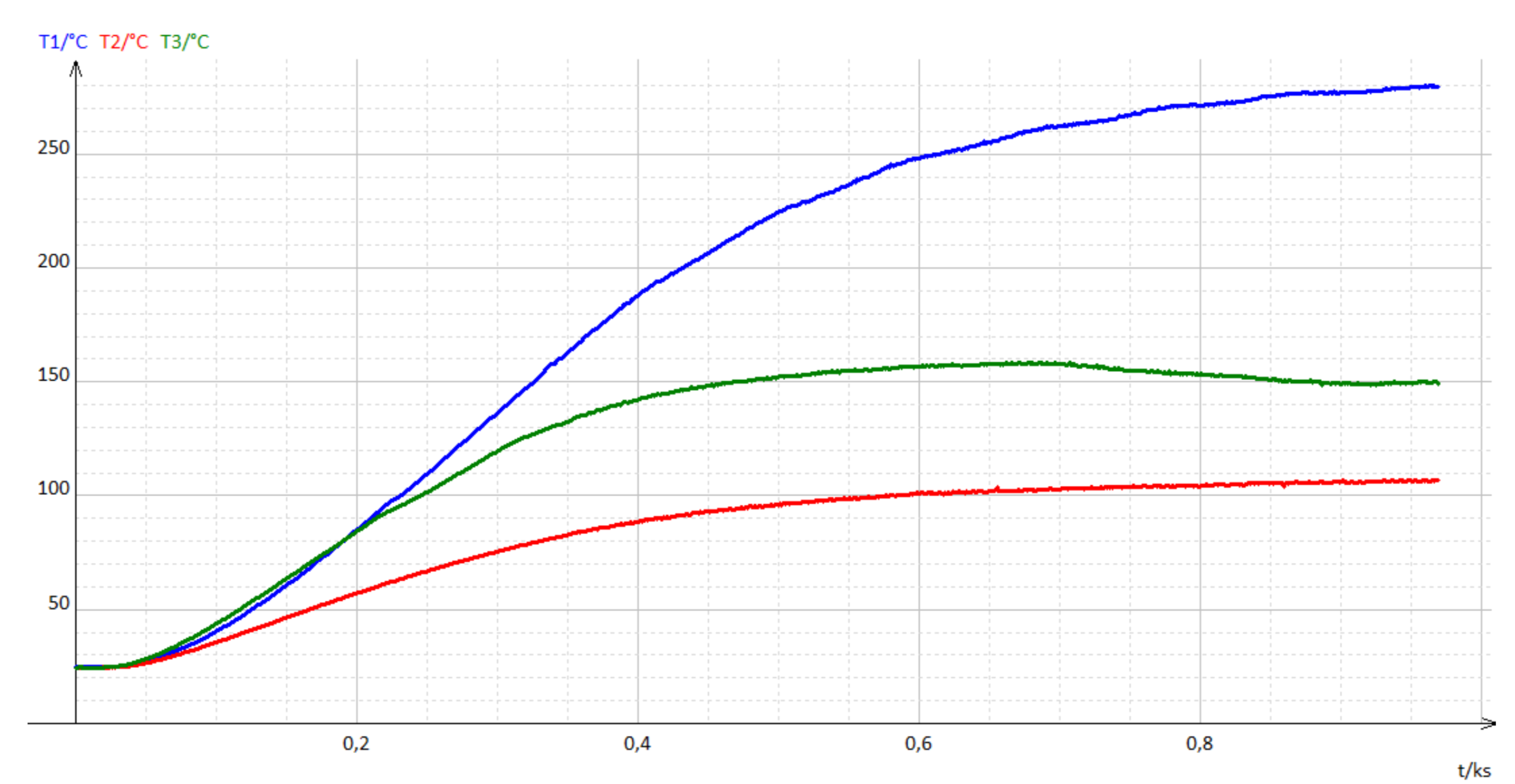
L’évolution de la température dans chaque cas est présentée sur la figure 24.

Figure 24.  Évolution de la température dans la pièce métallique

Pièce métallique seule (bleu – T1) ; avec caloduc (rouge – T2) ; avec radiateur seul (vert – T3)

Une fois encore, l’effet caloduc est très marqué : alors que la pièce métallique seule atteint 280°C après 950 s, le radiateur permet de limiter l’échauffement à 150°C et le dissipateur à caloducs à 100°C !

Le régime stationnaire avec le dissipateur à caloducs est effectivement atteint après 950 s, pour une température limite de 100°C. On va maintenant pouvoir déterminer la puissance thermique apportée à la pièce seule en évaluant la pente de la courbe au voisinage de 100°C, figure 25.

Figure 25.  Détermination la puissance thermique apportée à la pièce seule au voisinage de 100°C

Pièce métallique seule (bleu – T1) ; avec caloduc (rouge – T2) ;

Comme précédemment, la puissance thermique apportée vaut :

Finalement, notre dissipateur thermique à caloducs est donc capable d’évacuer 50 W de puissance thermique en régime stationnaire à une température de l’ordre de 100°C, permettant d’éviter l’échauffement intempestif de la pièce métallique.

Dans le cas du freinage d’un train, le frottement mécanique entre les pièces crée un échauffement thermique qu’il faut évacuer efficacement si on veut éviter une déformation du système, une perte de freinage, donc une situation potentiellement dangereuse. Un système de refroidissement à caloducs permettrait ainsi de diminuer sensiblement la température des disques de freinage et pourrait venir en complément du système de refroidissement actuel. Notons enfin qu’en pratique, les moteurs du TGV peuvent aussi servir de génératrice lors de la phase de freinage, convertissant ainsi l’énergie mécanique du train en énergie électrique.