Cuillère, mon beau miroir...

Catherine Simand Figure 1. Vue de l'intérieur d'une cuillère

Catherine Simand Figure 2. Vue de l'extérieur d'une cuillère

L'image de la bougie est inversée dans le premier cas et pas dans l'autre.

Pourquoi voyons-nous à l'envers quand nous regardons le creux d'une cuillère, et à l'endroit quand nous regardons le côté bombé ?

En première approximation la cuillère constitue un miroir sphérique qui est concave ou convexe, selon qu'on observe la réflexion sur la face creuse ou sur la face bombée. Pour la cuillère photographiée, on évalue entre 2 et 4 cm la valeur du rayon R de la sphère équivalente et à environ 10 cm la distance de la flamme à la surface réfléchissante.

Les constructions géométriques suivantes montrent la position de l'image de la bougie dans chacun des cas, miroir concave ou convexe. Les points C et F représentent le centre de courbure et le foyer du miroir sphérique de sommet S (en valeur algébrique SC= + ou - R, si le rayon de courbure est R).

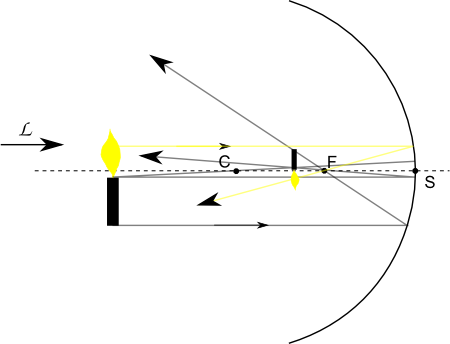Catherine Simand Figure 3. Miroir sphérique concave ; l'objet est placé avant le centre de courbure C

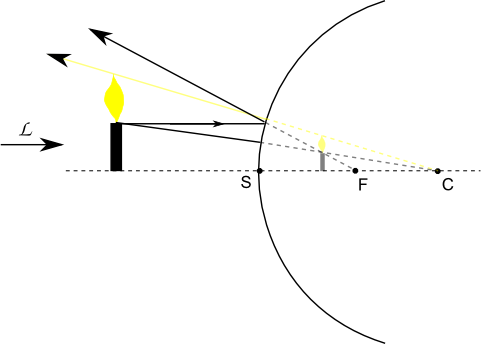Catherine Simand Figure 4. Miroir sphérique convexe

On constate que l'image est réelle et renversée dans le cas concave, et qu'elle est droite et virtuelle dans le cas convexe. L'image est plus petite que l'objet : si la bougie est à une distance 2R du miroir, on peut calculer le grandissement qui est de -1/3 (cas concave) ou +1/5 (cas convexe).

Nous vous proposons une sélection d'animations qui permettent de déterminer la position de l'image en fonction de celle de l'objet :

Comment pratiquement voit-on à travers un miroir ?

Un observateur ne perçoit une image que par les rayons lumineux qui pénètrent dans ses yeux. Les pupilles sélectionnent des rayons lumineux réfléchis par la surface du miroir et provenant initialement de points-objets situés du même coté que l'observateur par rapport au miroir. Par exemple ceux émis par la flamme de la bougie sont réfléchis par le miroir, passent (réellement ou non) par l'image de celle-ci et leur direction particulière leur permet de pénétrer dans l'œil de l'observateur.

Le cas du miroir sphérique convexe ou de la cuillère côté bombé correspond à la vision d'une image virtuelle, tout comme le miroir plan, plus usuel. L'observateur interprète les rayons lumineux réfléchis comme provenant de l'image de l'autre coté du miroir. Les images prévues pour la vision oculaire sont généralement virtuelles et localisées à grande distance, car l'oeil se fatigue moins s'il n'a pas à accommoder.

Comment peut-on voir une image réelle ? La vision d'images réelles se fait usuellement par l'intermédiaire de la lumière diffusée par un écran (projection, cinéma...). Il est possible de regarder directement une image réelle si elle n'est pas trop lumineuse et en accommodant correctement. Lorsque l'on regarde la cuillère côté creux, l'image réelle et renversée d'un objet lointain se forme juste devant le foyer F, et l'oeil accommode sur cette image, à 1 ou 2 cm devant le miroir. Il n'est pas toujours aisé de percevoir cette accommodation en avant de la cuillère. Elle est plus facilement perceptible si l'on regarde l'image d'un objet proche ou avec un miroir de plus grand rayon de courbure, parce que l'image est située plusieurs centimètres devant le miroir.

Comment expliquer la netteté des images photographiées ?

Elle est étonnante, car les miroirs sphériques ne sont pas stigmatiques et encore moins les faces de la cuillère aux formes plus complexes.

On est dans le cas du stigmatisme approché grâce aux conditions de Gauss qui sont réalisées pour le système bougie-cuillère-appareil photo ci-dessus. La bougie de diamètre 4 cm est à peu près centrée sur l'axe optique. L'appareil photo, situé à environ 1 m de la cuillère, est dans une direction faisant un angle d'une douzaine de degrés avec l'axe optique. Les rayons lumineux issus de l'objet, réfléchis par le miroir et atteignant l'objectif de l'appareil photo s'écartent assez peu de l'axe, l'inclinaison est au maximum de 12 degrés (Arctan (2/10) ≃ 11°).

Pour des objets plus écartés de l'axe optique, les conditions de Gauss ne sont plus remplies. On observe de la distorsion (en barillet dans les deux cas photographiés) : les droites sont courbées, les angles sont modifiés et les images sont déformées. On peut s'en convaincre en observant un papier quadrillé par réflexion sur une cuillère ou une louche.

Applications des miroirs sphériques

Les miroirs concaves sont utilisés pour leur capacité à concentrer la lumière provenant d'une source lointaine (télescope, four solaire...) ou à transmettre en faisceau quasi parallèle la lumière émise par une petite lampe (lampe de poche, phare d'automobile). Ils sont aussi utiles quand il est pratique d'obtenir une image plus grande que l'objet, par exemple comme miroir de toilette grossissant. Le rayon de courbure du miroir est suffisant pour que, naturellement, on place son visage entre le foyer et le sommet.

Les miroirs convexes peuvent former des images petites d'un objet éloigné et sont alors utiles pour leur grand champ de vision : miroirs de surveillance, rétroviseurs d'automobiles, ou miroirs au coin de rues pour permettre de voir derrière un obstacle.