Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
L'holographie numérique rapide ou comment suivre des objets en 3D avec une seule caméra.
03/06/2013
Résumé
Cet article présente le principe d'enregistrement et de restitution d'un volume contenant des micro-objets par l'holographie numérique. Ce travail a été réalisé en collaboration avec Jean-Louis Marié, Michel Lance, Nathalie Grosjean et Loïc Méès du Laboratoire de Mécanique des Fuides et d'Acoustique de l'École Centrale de Lyon et Jérome Gire et Corinne Fournier du Laboratoire Hubert Curien de l'Université de St Etienne.
Table des matières
I. Présentation de l'holographie numérique en ligne
1. Introduction
Les mesures optiques sont non-intrusives et précises. Elles sont incontournables dans de nombreux domaines de la recherche et du développement comme en mécanique des fluides, en géophysique (turbulence atmosphérique, transport de sédiments), dans le secteur médical (écoulements dans des microcavités), dans l’industrie automobile (sprays, émissions polluantes), dans l’industrie chimique (écoulements multiphasiques réactifs). Parmi ces techniques, l’holographie numérique recèle un potentiel considérable, en raison de sa relative simplicité de mise en oeuvre et de son caractère tridimensionnel.
2. Contexte historique
Le principe de l'holographie a été découvert en 1948 par Dennis Gabor. Mais son utilisation n'a été possible qu'avec l'apparition des premiers lasers dans les années 1960.
Les premiers hologrammes étaient enregistrés sur des plaques photographiques. Cela rendait l'utilisation de cette technique contraignante de par le temps et le savoir faire nécessaire au développement chimique des plaques. Le passage de l'holographie optique vers le numérique s'est effectué dès les années 1970. Et depuis les années 2000, l'holographie numérique n'a cessé de se développer bénéficiant des progrès technologiques en matière de capteurs de caméra, de capacité de stockage de données et de puissance de calcul des ordinateurs.
3. Principe d'enregistrement
L'holographie numérique est une technique d'imagerie optique qui offre l'énorme avantage d'enregistrer l'information tridimensionnelle d'un objet sur un seul support bidimensionnel, contrairement aux techniques classiques d'imagerie par stéréoscopie. Elle permet ainsi d'accéder à la taille, la forme et la position dans l'espace de l'objet étudié.
La configuration présentée ici est un montage dit « en-ligne » où la caméra est placée face à la source lumineuse (laser). Ce montage se prête particulièrement à l'étude de micro-objets répartis dans un volume. Il est robuste aux vibrations, simple à mettre en oeuvre et nécessite que peu de puissance lumineuse.
On s'intéresse ici à l'utilisation de l'holographie pour étudier le comportement de toutes petites gouttelettes d'eau (60 microns) dans un écoulement turbulent. L'illustration est donnée sur la figure 1, photo prise en pause longue qui permet de visualiser les trajectoires des gouttelettes.
Source - © 2009 D. Chareyron
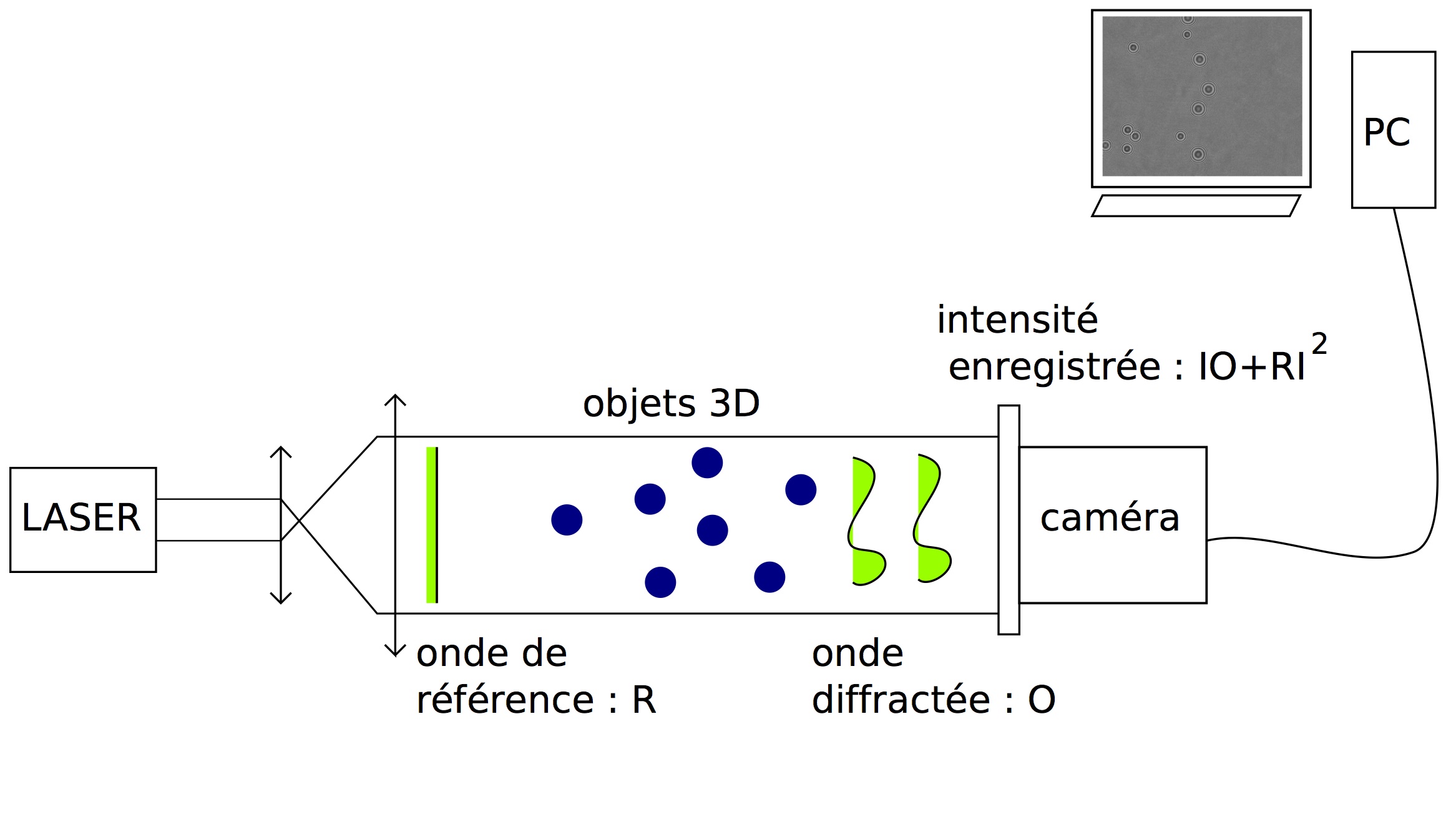
Le montage utilisé est présenté sur la figure 2. L'enregistrement d'un hologramme consiste à éclairer un objet par une source de lumière cohérente. Les interférences entre l'onde de référence et l'onde diffusée par l'objet sont alors enregistrées sur le capteur de la caméra. C'est la phase de l'onde diffusée par l'objet qui contient l'information 3D de l'objet.
Les informations 3D des particules illuminées sont enregistrées sur un capteur 2D et sont ensuite reconstruites grâce aux propriétés de cohérence de la source de lumière utilisée. Pour une bonne cohérence spatiale, la source doit être ponctuelle. La cohérence temporelle elle, est liée au caractère monochromatique de la source.
Source - © 2009 D. Chareyron
On note R l'onde de référence et O l'onde diffractée. : Et où φ R représente la phase de l'onde de référence et φ la phase de l'onde émise par l'objet. L'amplitude totale résultant de l'interférence de ces deux ondes est : Le capteur photosensible enregistre l'intensité de l'onde résultante : Ainsi, l'information 3D est contenue dans la phase de l'amplitude du signal est enregistrée dans l'hologramme sous la forme de franges d'amplitude modulée, associées au terme . |
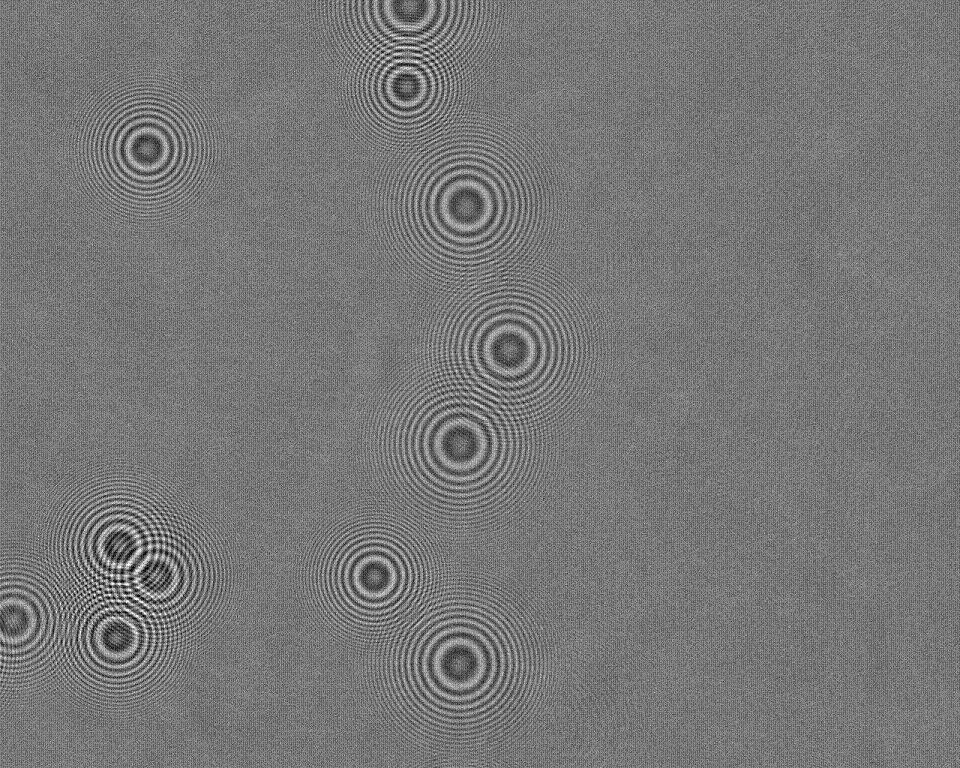
Les hologrammes acquis en ligne ont aussi l'avantage d'être partiellement interprétables à l'oeil nu.
Source - © 2009 D. Chareyron
4. Restitution ou mise au point numérique
Avant l'ère des caméras numériques, il était nécessaire dans un premier temps de développer les plaques sur lesquelles l'hologramme était enregistré. La restitution, c'est à dire l'étape permettant de remonter aux informations initiales sur l'objet était ensuite réalisée par ré-éclairement de celui-ci par la même onde de référence R que celle utilisée lors de l'enregistrement.
Aujourd'hui, à l'aide de l'holographie numérique, la restitution de l'hologramme est fondée sur la simulation numérique de la diffraction. On parle alors de mise au point numérique.
Source - © 2009 C. Fournier
Figure 4. Mise au point numérique ou restitution
L'enregistrement sous forme numérique de l'hologramme modifie le rapport signal sur bruit et limite les fréquences enregistrées à la fréquence de Nyquist Shannon. Les paramètres entrant en compte sont : le nombre de pixels du capteur, la taille de chacun des pixels, l'homogénéité de la sensibilité du capteur, c'est-à-dire sa réponse à un éclairage uniforme et sa dynamique. Une grande dynamique permet un bruit de quantification plus faible et donc une meilleure précision de positionnement des objets et de mesure de taille.
La figure 5, illustre le principe de reconstruction par mise au point numérique. Un algorithme vient analyser chaque plan selon l'axe z afin de déterminer la position des particules dans le volume. Dans l'illustration, on cherhce à retrouver la composante z d'une mire placée dans le volume éclairé.
Source - © 2009 C. Fournier
5. Reconstruction
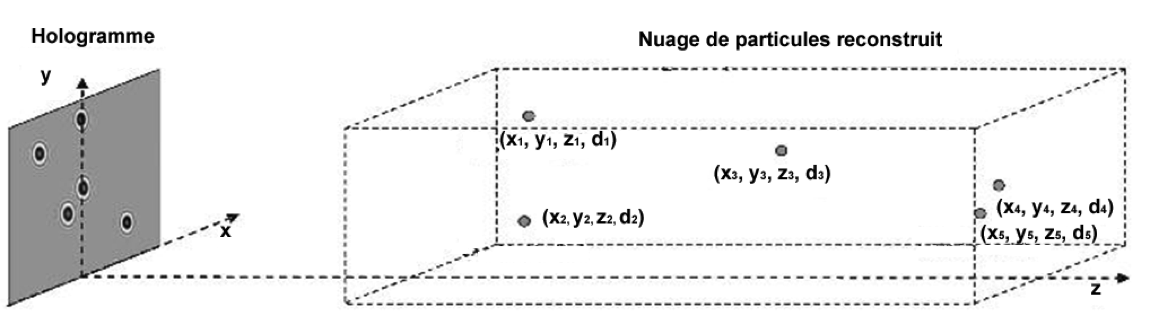
L'étape de reconstruction consiste à analyser les plans restitués pour en déduire la position et la taille des objets restitués.
Source - © 2009 C. Fournier
Figure 6. Étape de reconstruction
II. Reconstruction des trajectoires des gouttelettes
1. Suivi des objets
L'utilisation d'une caméra rapide permet de suivre l'évolution des objets dans le temps. Il s'agit de choisir une fréquence d'échantillonnage suffisamment grande pour ne pas perdre les objets d'une image à la suivante et estimer avec précision leurs trajectoires.
La video présentée sur la figure 7 correspond à un enregistrement des hologrammes à une fréquence de 1 000 images / seconde.
Source - © 2009 D. Chareyron
Figure 7. Extrait de l'enregistrement à 1 000 images / seconde
La séquence est visualisée ici au ralenti.
Les algorithmes de tracking utilisés pour remonter aux trajectoires de particules sont nombreux et reposent sur des critères plus ou moins compliqués comme la prise en compte de la vitesse de la particule au pas précédent (amplitude et direction), l'accélération, la forme de l'objet, etc.
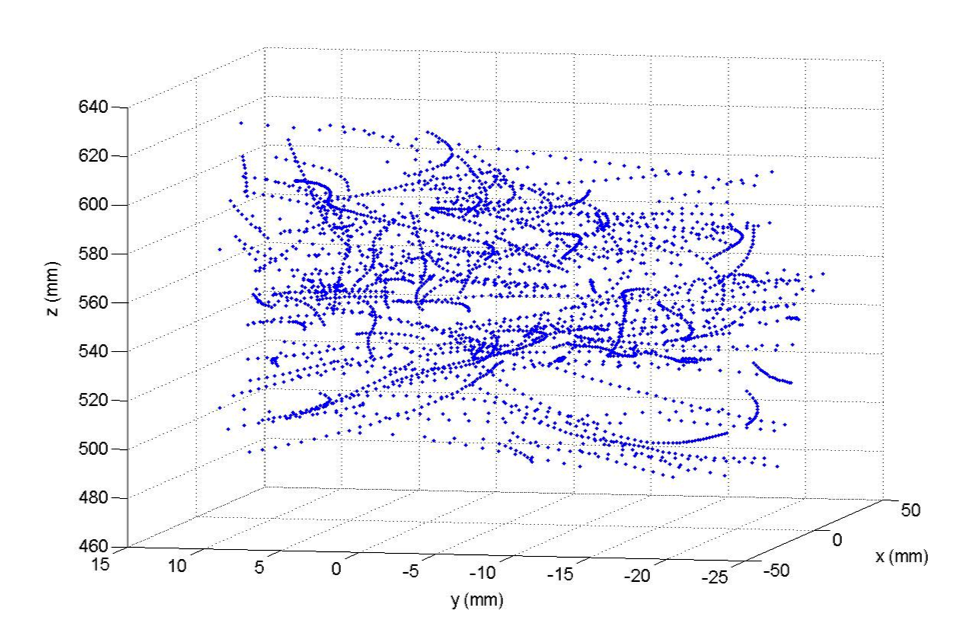
La figure 8 présente la reconstruction de quelques dizaines de trajectoires.
Source - © 2009 D. Chareyron
Figure 8. Reconstruction de trajectoires
2. Diagnostiques sur les diamètres
L'holographie numérique permet d'avoir aussi accès à la taille des particules enregistrées. Il est alors possible de suivre à chaque pas de temps la valeur du diamètre des goutellettes étudiées.
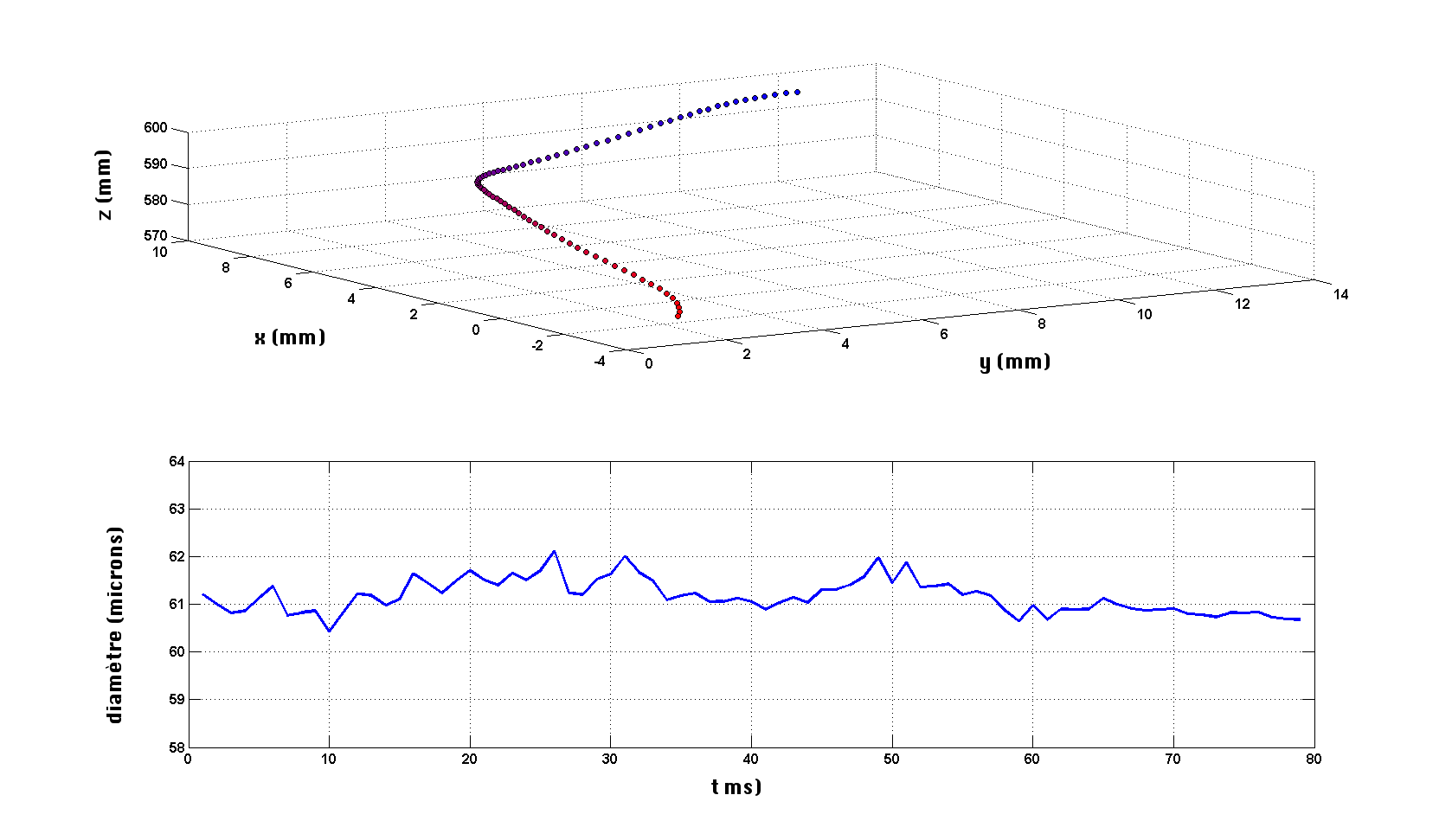
Sur la figure 9 une trajectoire est reconstruite et on peut observer la valeur du diamètre détecté par l'instrumentation au cours du temps. Chaque pas de temps correspond à 1 ms.
Source - © 2009 D. Chareyron
Le temps est codé du bleu vers le rouge.
La valeur du diamètre reste constante le long de la trajectoire, ce à quoi on s'attend pour des gouttelettes d'eau à température ambiante. L'écoulement est suffisamment dilué pour ne pas voir de coalescence de gouttes entre elles. Les petits écarts correspondent au bruit de la mesure qui est très faible, ici 2 % de la mesure.
Conclusion
L’holographie reste une des seules techniques de mesure en mécanique des fluides permettant d’estimer la taille, la position, la vitesse d’objets répartis dans un volume. Comme toute technique elle possède ses limites :
- le nombre d’objets ne doit pas être trop important (environ moins d’une centaine de particules),
- pour des raisons de contraste la taille des objets ne doit pas être inférieure à environ 10 µm (dans un montage à grandissement un, c'est-à-dire sans objectif, cette taille minimale peut être diminuée mais au détriment du champ d’étude).
- la précision transversale (perpendiculairement à l’axe optique) est 50 fois plus élevée que la précision longitudinale (profondeur).
L’holographie numérique en ligne présente l’énorme avantage d’être simple et rapide à mettre en oeuvre (environ une demi journée pour une personne inexpérimentée) et utilisable sur des objets solides ou liquides. Dans un contexte industriel ces avantages sont primordiaux. De plus, les dernières avancées technologiques dans le domaine des caméras rapides, avec des résolutions de plus de un million de pixels à une cadence de plus de 10000 images par seconde, permettent de suivre des objets dans le temps ou encore de visualiser la topologie de champs de concentration ou de température.
Références :
- Laboratoire de Mécanique des Fuides et d'Acoustique de l'École Centrale de Lyon.
- Laboratoire Hubert Curien de l'Université de St Etienne.
- Optique pour l'ingénieur : cours d'optique en libre accès de l'université du Maine.
Pour citer cet article :
L'holographie numérique rapide ou comment suivre des objets en 3D avec une seule caméra, Delphine Chareyron, Corinne Fournier, juin 2013. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Holographie-gouttes-Chareyron.xml
