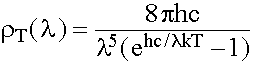Le corps noir

Un corps noir est un corps qui absorbe, sans la réfléchir ni la diffuser, toute l'énergie électromagnétique qu'il reçoit. Ainsi, une boite avec une toute petite ouverture est généralement une bonne approximation d'un corps noir. Un tel "corps noir" reçoit de l'énergie, s'il n'en émettait pas, sa température augmenterait indéfiniment... Ceci est irréaliste, un corps noir réémet donc l'énergie qu'il a absorbée sous forme de rayonnements électromagnétiques. La quantité d'énergie réémise dépend de sa température. Ainsi, on a une "loi de rayonnement du corps noir" qui donne la valeur de l'énergie émise en fonction de la température du corps noir.

Toutefois, lorqu'on a dit cela, on n'a fait qu'effleurer le problème. En fait, le problème du corps noir est un problème qui a été à l'origine, par la « catastrophe ultraviolette » qu'il a engendrée, de la révolution quantique... Lire sur ce thème l'article « Fenêtre ouverte sur la mécanique quantique » par Gabrielle Bonnet.

Les physiciens se sont intéressés à la loi de rayonnement du corps noir dès le début du vingtième siècle, et ont calculé, en vertu des lois de la physique classique, la densité d'énergie rayonnée dans chaque gamme de longueur d'onde :

ρ(λ,T) dλ = 8 π k T /λ⁴ dλ

ρ(λ,T) dλ est la quantité d'énergie émise correspondant à des longueurs d'onde comprises entre λ et λ + dλ, par un corps noir à la température T.

k, constante de Boltzmann, vaut k = 1,3806503 × 10^-23 m².kg.s^-2.K^-1

Toutefois, cette formule ne correspond pas à l'expérience.

Gabrielle Bonnet

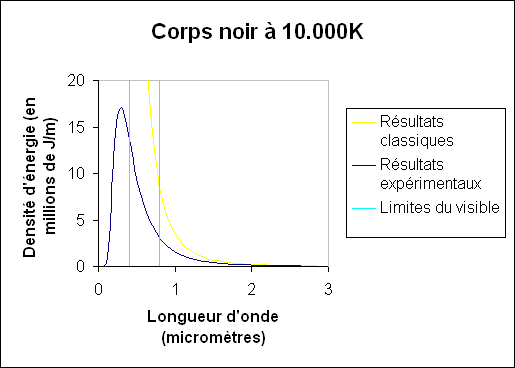
Figure 1. Corps noir à 10.000K

Alors que les courbes théoriques et expérimentales correspondent raisonnablement bien pour les grandes longueurs d'onde, il n'y a plus du tout accord pour les petites longueurs d'ondes où on voit les valeurs expérimentales être beaucoup plus faibles que les valeurs théoriques qui, elles, devraient tendre vers l'« infini ». C'est ce que l'on a appelé à l'époque la « catastrophe ultraviolette ».

Il a fallu l'avènement de la physique quantique pour expliquer cette « catastrophe » et trouver enfin moyen de faire correspondre théorie et expérience.

Dans la pratique, la loi de rayonnement du corps noir décrit convenablement le rayonnement, sous l'effet de la chaleur, par exemple d'un filament chauffé. Ainsi, les lampes à incandescence émettent un rayonnement qui obéit à la loi du corps noir.

De la même façon, le spectre continu émis par les étoiles (et dont une partie va être absorbée, donnant ainsi le spectre de raies qui nous est familier) peut être décrit aussi convenablement par la loi de Planck.

Le maximum de la courbe donnant la densité d'énergie émise en fonction de la longeur d'onde est donné par la loi de Wien :

λ_max = h c / (4,965 kT).

et l'énergie totale émise est donnée par la loi de Stefan :

Flux énergétique émis intégré sur toutes les longeurs d'ondes = σ T⁴ où σ = 5,67 × 10^-8 S.I.

On constate tout d'abord que la quantité totale d'énergie émise croît avec la température du corps noir : plus le corps est chaud, plus il émet de l'énergie électromagnétique.

On constate ensuite que le maximum d'énergie est émis pour une longeur d'onde qui décroît avec la température. Par conséquent, lorsque la température d'un corps s'élève, il émet d'abord dans l'infrarouge (ainsi, on peut repérer un être vivant la nuit grâce à des lunettes à infrarouge qui permet de déceler le rayonnement produit par tout corps chaud). Ensuite, lorsqu'il commence à émettre dans le visible, ce corps est d'abord rougeoyant, puis vire au jaune, puis au blanc...

Lorsque la température devient très intense, comme dans certaines étoiles, la lumière émise va l'être principalement dans les courtes longeurs d'onde, et l'objet nous apparaitra donc bleu.

La loi de rayonnement du corps noir est utilisée régulièrement dans sa forme la plus simple (variation de la couleur avec la température), dès la de seconde, pour déduire de sa couleur la température approchée d'une étoile. La plupart des personnes qui ont fait des études supérieures ont déjà vu la loi de Planck et ses corollaires (loi de Wien ou loi de Stefan).

Il n'est pour autant pas toujours évident que ce qui est quantifié, dans la loi du corps noir, ce ne sont pas les niveaux d'énergie de la matière (comme dans le cas des spectres d'émission ou d'absoption atomiques ou moléculaires du programme de seconde), mais le rayonnement lui-même.

Nous espérons que cet article bref favorisera une meilleure compréhension de cette double quantification (de la matière, et du rayonnement) qui existe en physique quantique, et de la façon dont cela explique l'universalité de la loi du corps noir, son indépendance par rapport au matériau qui constitue ce corps.