Analyse numérique appliquée à une source de tension, en langage python

Dans un premier temps, on importe les bibliothèques python nécessaires au traitement des données et à l'affichage des graphiques, figure 2.

Figure 2.  Importation des bibliothèques python utilisées

On consigne les valeurs de tension et de courant obtenues expérimentalement, figure 3.

Les vecteurs U et I sont définis comme des tableaux (array) faisant appel à la bibliothèque numpy (np). L'intensité a été relevée en milliampère, d'où la multiplication des valeurs par 10^-3, qui se note en python 10**(-3).

On remarque que les items d'un vecteur sont séparés par des virgules. La notation décimale est codée par un point.

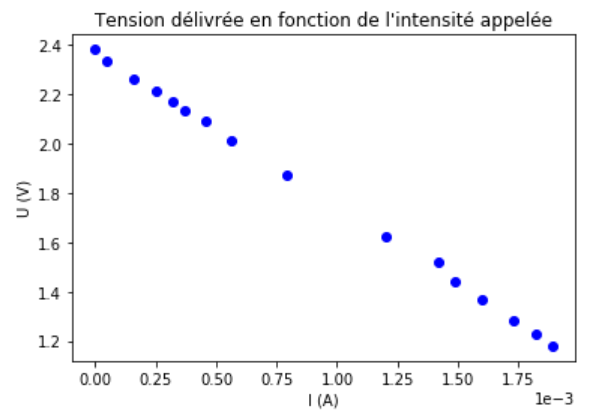
On propose ici, simplement pour vérifier, un premier tracé des points. La fonction plot appelle la bibliothèque pyplot (plt), on renseigne d'abord l'axe des abscisses (I), l'axe des ordonnées (U) et le format du tracé (bo) : des points ronds tracés en bleu.

La fonction plt.show() permet d'afficher la figure a l'ecran.

Figure 3.  Valeurs de tension et courant mesurées et premier tracé

On obtient la figure 4.

Figure 4.  Premier tracé des valeurs expérimentales correspondant au code de la figure 3

Maintenant, nous ajoutons le titre, les axes et les unités sur le tracé, figure 5.

On affiche les valeurs d'intensité sous la forme de l'écriture scientifique pour plus de visibilité en utilisant la fonction ticklabel_format de la manière suivante :

ticklabel_format (écriture scientifique, axe concerné, prise en compte pour toutes les valeurs du vecteur).

Figure 5.  Code Python pour le tracé de la caractéristique tension - courant de la source de tension

On obtient la caractéristique tension - courant, figure 6.

Figure 6.  Représentation graphique de la caractéristique tension - courant de la source de tension

Nous modélisons les données expérimentales à l'aide d'une regression linéaire. Nous utilisons la fonction pré-existante linregress dans la bibliothèque scipy.stats, figure 7.

La fonction renvoie :

On demande ensuite, à l'aide de la commande print, d'afficher à l'écran les valeurs trouvées. Les termes entre cotes "" s'écrivent tels quels, alors que les autres renvoient aux valeurs des variables. Pour obtenir l'affichage du caractère Ω, pour les ohms, le langage python utilise le caractère Unicode 937.

Figure 7.  Code python de la régression linéaire

Le code renvoie les valeurs suivantes :

E_g = 2.3673840162590967 V

r_g = 622.8309185078344 Ω

Pour garder du sens physique par rapport à la précision donnée par les multimètres, on affiche une valeur arrondie du résultat calculé à l'aide de la fonction round. On choisit de ne garder que 2 décimales pour la valeur de la tension à vide et une seule décimale pour la valeur de la résistance interne du générateur, figure 8.

Figure 8.  Code python pour arrondir les valeurs de la tension à vide et de la résistance interne

Le code renvoie donc les valeurs suivantes :

E_g = 2.37 V

r_g = 622.8 Ω

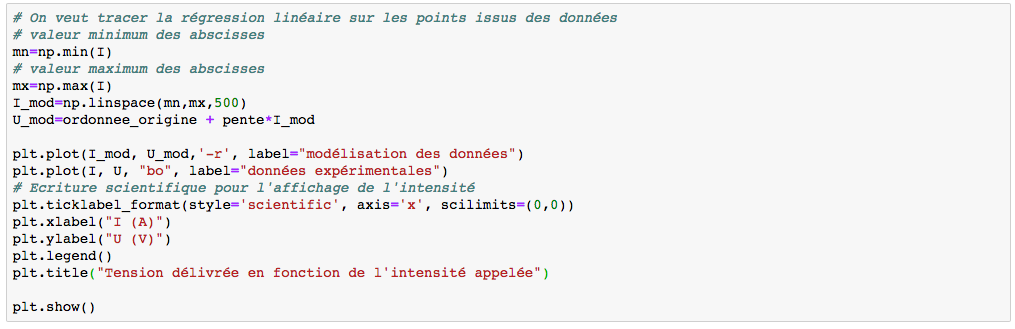
Pour tracer la regression linéaire calculée à partir des données, nous avons besoin de créer deux vecteurs : I_mod correspondant aux abcsisses et U_mod correspondant aux ordonnées. On choisit pour I_mod un vecteur contenant 500 points, avec comme valeurs minimales et maximales les mêmes que celles obtenues expérimentalement. La création du vecteur est réalisée à l'aide de la fonction linspace, de la manière suivante :

Définition d'un vecteur (linspace) partant de la valeur de I minimum (mn), à la valeur de I maximum (mx), contenant 500 points (500).

La modélisation de la tension U_mod est réalisée selon le fonctionnement de la source de tension réelle : U = E_g - r_g I

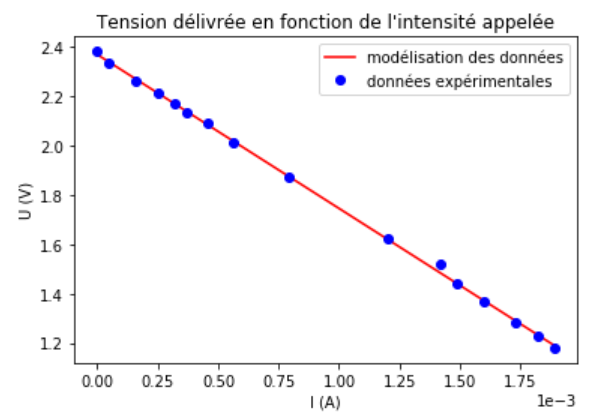
On trace la modélisation à l'aide d'une ligne rouge (-r). On ajoute une légende (label) pour chaque courbe, l'affichage est gérée par la fonction plt.legend().

Figure 9.  Code python pour tracer la régression linéaire sur les données

Le programme affiche le graphique, figure 10.

Figure 10.  Représentation graphique de la caractéristique tension - courant de la source de tension en bleu et sa modélisation par une régression linéaire en rouge

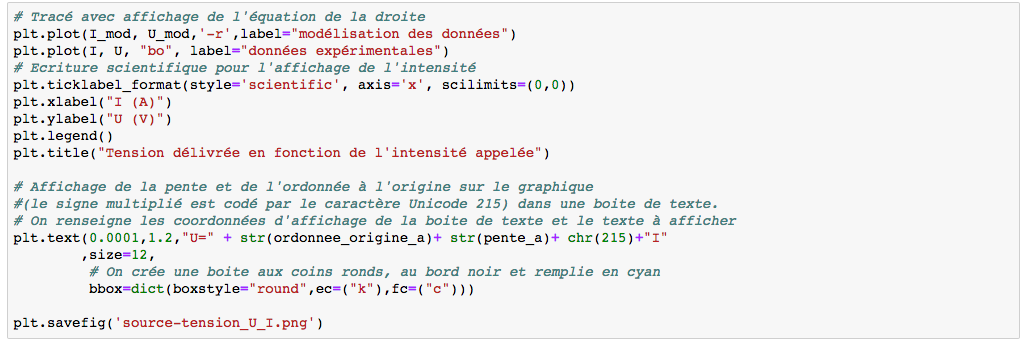
On souhaite ajouter l'équation de la régréssion linéaire sur le graphique, figure 11. On utilise la fonction plt.text de la manière suivante :

Définition de la boite de texte plt.text ( position X de la boite, position Y de la boite, texte contenu dans la boite, taille de la police, puis on définit les attibuts de la boite (bbox) : boite aux coins ronds, au bord noir et remplie en cyan).

La fonction plt.savefig permet d'enregistrer la figure.

Figure 11.  Code python pour afficher les données expérimentales, la régression linéaire et l'équation de la droite

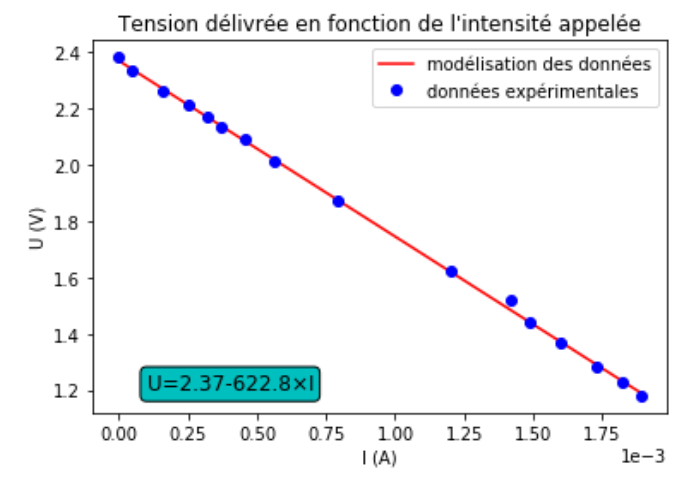
Le programme affiche le graphique, figure 12.

Figure 12.  Représentation graphique de la caractéristique tension - courant de la source de tension en bleu et sa modélisation par une régression linéaire en rouge

Les données constructeur du GBF, indiquent une valeur de résistance de sortie du GBF de 600 Ω.

Dans ce permier exemple volontairement simple, nous avons choisit de ne pas faire apparaître de barres d'erreurs. Ce sera l'objet d'un prochain article.