Principe du passage de l'analogique au numérique

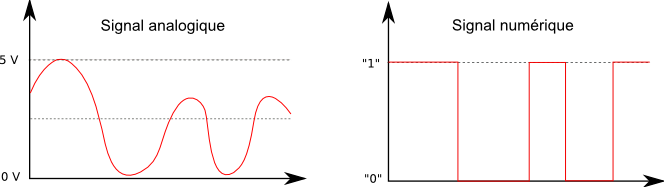
Un signal analogique est un signal continu qui peut prendre une infinité de valeurs, alors que le signal numérique est un signal discret (discontinu), qui se résume en une succession de « 0 » et de « 1 ».

Figure 1.  Signal analogique et signal numérique

L’objectif de la numérisation est de transformer le signal analogique qui contient une quantité infinie d'amplitudes en un signal numérique contenant lui une quantité finie de valeurs.

Le passage de l'analogique au numérique consiste en 2 étapes successives : l'échantillonnage et la conversion analogique-numérique (CAN).

Figure 2.  Dispositif d'enregistrement numérique d'un son

Le nombre d'échantillons composant le signal numérique devra être suffisamment grand pour pouvoir représenter le signal analogique de départ mais pas trop grand non plus pour ne pas être trop volumineux.

Deux facteurs devront être ajustés pour répondre à ce cahier des charges : la précision et la rapidité.

Le premier paramètre à fixer est la vitesse à laquelle seront prélevés les échantillons pour que la reconstruction du signal de sortie soit fidèle au signal d'entrée. La fréquence d'échantillonnage doit être suffisamment grande. En effet, si celle-ci est trop faible, les variations rapides du signal ne pourront être retranscrites.

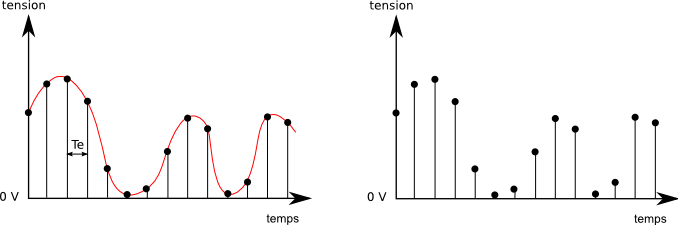
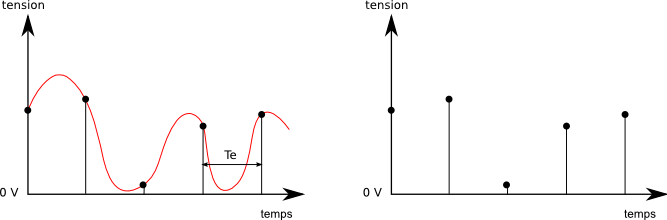
Voici deux exemples d'échantillonnage du même signal pour deux fréquences ${f_e}_1=\frac{1}{{T_e}_1}$ et ${f_e}_2=\frac{1}{{T_e}_2}$.

Figure 3.  Signal échantillonné à T_e1

Figure 4.  Signal échantillonné à T_e2>T_e1

Dans le premier exemple, la fréquence d'échantillonnage choisie permet de reproduire les variations du signal. Par contre dans le second exemple, il est clair que les échantillons recueillis ne sont pas suffisants pour reconstruire le signal d'origine.

Le théorème de Shannon permet de connaître la fréquence d'échantillonnage à choisir pour un signal donné :

Pour reconstruire un signal de sortie de manière fidèle au signal d'entrée, il faut choisir une fréquence d'échantillonnage au moins deux fois supérieure à la fréquence maximale contenue dans le signal d'entrée.

$f_e>2f_{\max }$

Si cette règle n'est pas respectée, des fréquences parasites qui n'appartiennent pas au signal de départ apparaissent. Ce phénomène est le repliement spectral ou aliasing.

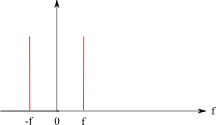
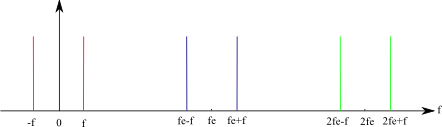
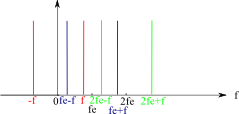
Exemple 1 : Cas d'un signal sinusoïdal

Figure 5.  Spectre d'un signal sinusoïdal
fe respecte le critère de Shannon Figure 6. Spectre du signal sinusoïdal échantillonné à $f_e>2f_{\max }$	fe ne respecte pas le critère de Shannon Figure 7. Spectre du signal sinusoïdal échantillonné à $f_e<2f_{\max }$

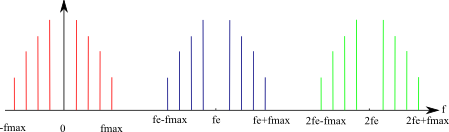
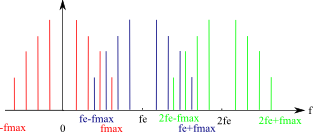
Exemple 2 : Cas d'un signal quelconque

fe respecte le critère de Shannon Figure 8.  Spectre d'un signal quelconque échantillonné à $f_e>2f_{\max }$

fe ne respecte pas le critère de Shannon Figure 9.  Spectre d'un signal quelconque échantillonné à $f_e<2f_{\max }$

Lorsque le critère de Shannon n'est pas respecté, la fréquence d'échantillonnage est trop proche de la fréquence maximale du signal et on observe le mélange des fréquences hautes et des fréquence plus basses (voir figure 5 à 9).

On observe que dans les deux exemples ci-dessus il devient impossible d’effectuer une séparation correcte des fréquences lorsque le critère de Shannon n'est pas respecté.

La précision ou résolution du signal obtenu en sortie va dépendre du convertisseur utilisé, autrement dit de l'électronique mise en oeuvre. La limite théorique de la résolution est définie par le nombre de bits du convertisseur analogique numérique.

L'exemple de la figure 1 montre un signal analogique codé sur 1 bit, seules deux valeurs sont possibles pour ce bit soit « 0 » soit « 1 ». La précision est alors très faible et ne permet pas un résultat satisfaisant.

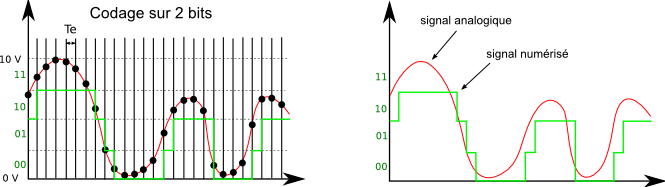
Lorsque le codage s'effectue sur 2 bits, chaque bit pouvant prendre deux valeurs (« 0 » ou « 1 »), 2² valeurs seront stockées soit un pas de quantification de 2,5 V $\left(\frac{10}{4}\right)$.

Dans cet exemple, le signal a une amplitude de 10 volts :

• 0 à 2,5 V, le code sera « 00 »
• 2,5 V à 5 V, le code sera « 01 »
• 5 V à 7,5 V, le code sera « 10 »
• 7,5 V à 10 V, le code sera « 11 »

Plus le nombre de bits sera important et meilleure sera la précision, mais plus le signal occupera de mémoire !

Figure 10.  Signal analogique codé sur 2 bits

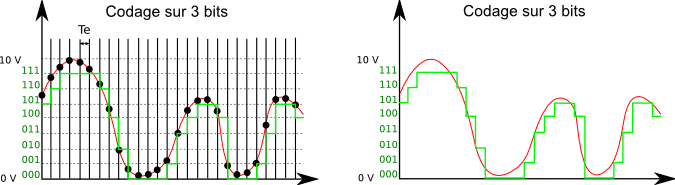
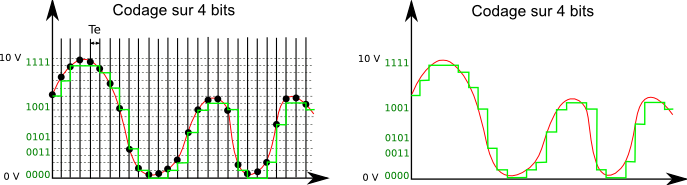
Voici deux exemples de codage sur 3 et 4 bits à fréquence d'échantillonnage fixe.

Figure 11.  Signal analogique codé sur 3 bits

Figure 12.  Signal analogique codé sur 4 bits

Le réglage des paramètres (précision et rapidité) se fera donc en fonction des contraintes (taille du signal… ) et de l'utilisation souhaitée. Il faudra donc faire des compromis entre précision et taille du signal.

De façon générale la précision, liée au nombre de bits, dépend de la technologie du convertisseur utilisé.

Les avantages des systèmes numériques sont certains. Cependant, notons que le passage dans le numérique s'accompagne d'une perte d'information puisque du signal analogique ne sont conservés que des échantillons. L'enjeu est donc de prendre suffisamment d'échantillons avec une cadence acceptable pour reconstruire au mieux le signal de départ tout en gardant un signal qui ne soit pas trop gourmand en espace.

Article suivant : « Comment convertir un signal analogique en signal numérique au laboratoire »

Références

Article précédent : « De l'intérêt de passer dans le monde numérique ».

Dossier : « Traitement du signal ».