Activer le mode zen
Ressource au format PDF
Classification
L’éolienne a le vent en poupe !
Construction d'une éolienne de Savonius
12/10/2020
Travail réalisé dans le cadre des XXVIIe Olympiades de Physique sous la tutelle de Romain Dardevet, professeur de Physique-Chimie.
Résumé
Qui n’a jamais été étonné de voir une éolienne tourner dès que le vent se lève ? Celle-ci convertit par sa rotation l’énergie cinétique du vent en électricité.
Se soulèvent alors quelques questions : quelle énergie peut être récupérée de cette rotation ? Quelles données physiques peuvent-être étudiées ? Comment est produite l’énergie électrique des éoliennes ?
Dans le cadre de ce projet nous avons choisi d'étudier le modèle d’éolienne Savonius hélicoïdal qui de par sa forme et ses dimensions permet une analyse dans des souffleries en laboratoire plus aisée. Tout d’abord nous avons élaboré un protocole afin d’établir un rendement, puis nous avons souhaité produire un alternateur artisanal afin de bien comprendre la physique en jeu.
Table des matières
Ce travail fait l'objet de deux articles. Dans le premier, on présente l'éolienne de Savonius et la caractérisation d'un prototype expérimental. Dans le deuxième article, on s'intéresse à la fabrication complète (rotor et stator) de l'éolienne étudiée. Lire le premier article : L’éolienne a le vent en poupe - Caractérisation d'une éolienne de Savonius - rendement
1. Construction d'une éolienne
Nous avons choisi de fabriquer une éolienne de toutes pièces.
Cette maquette, figure 1, a connu quelques évolutions tout au long des expérimentations qui ont suivi.
Figure 1. Dimensions et constitution de l'éolienne |
Remarque : le cadre permet de maintenir l’éolienne et d’assurer la solidarité avec la soufflerie dans laquelle elle sera testée.
2. Réalisation du rotor
2.1 Mesure du champ magnétique créé par un aimant
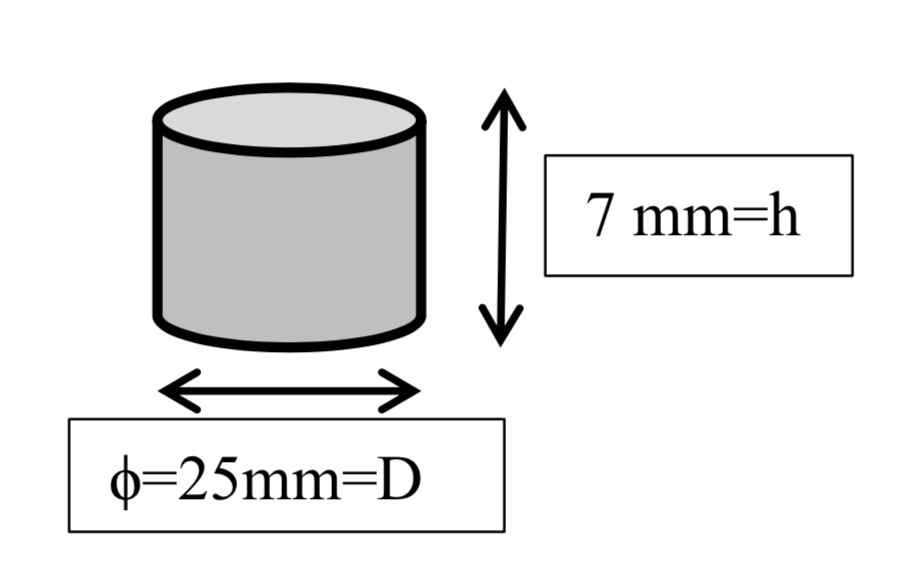
Afin de réaliser l’alternateur, nous avons acheté des aimants. Nous avons commencé par mesurer le champ magnétique créé par un seul aimant en fonction de la distance à l'aimant, à l’aide d’un teslamètre, figure 2.
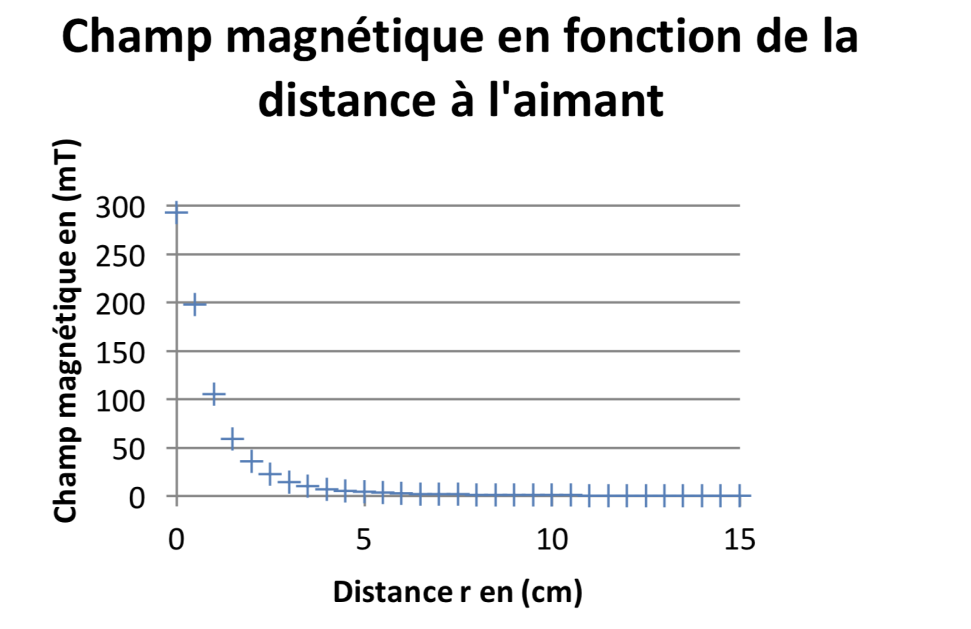
Nous avons obtenu le champ magnétique en fonction de la distance, figure 3.
Le champ magnétique créé par un dipôle magnétique et la distance sont liés par la relation :
Avec M le moment magnétique de l'aimant (Am-2), r la distance à l'aimant (m), et μ0 la perméabilité magnétique du vide (μ0 = 4π.10-7 TmA-1).
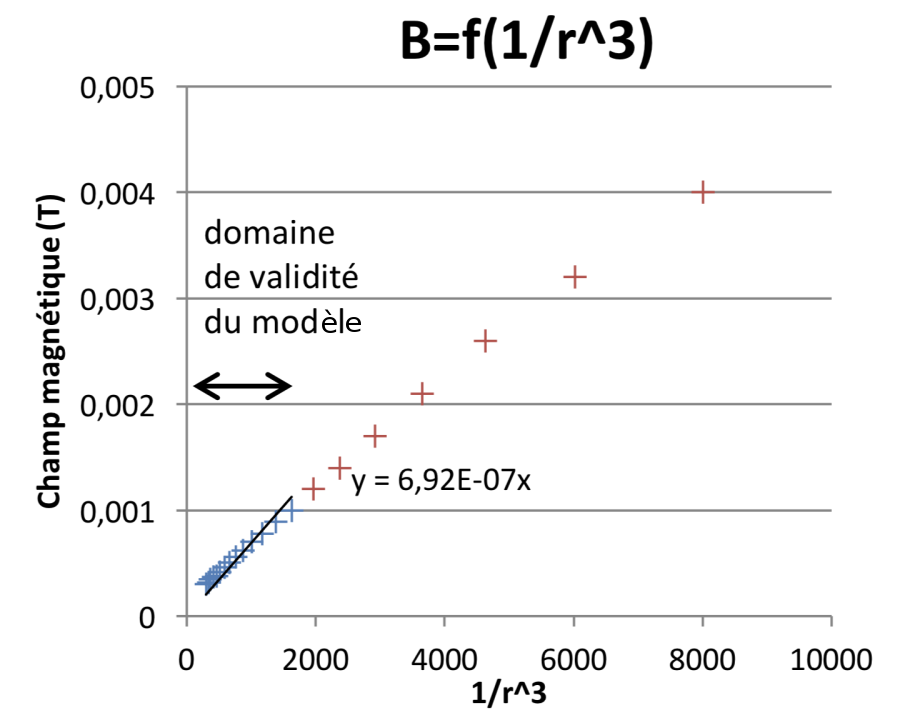
Cette relation n’est valable qu’à grande distance comme le montre la courbe suivante, figure 4.
On constate qu’il y a bien proportionnalité pour une distance à l’aimant assez grande, soit 1/r3 très petit. En outre nous prenons en compte ici les points au-delà de 8 cm.
À partir du coefficient de la droite il est possible de retrouver la valeur du moment magnétique en mesurant la pente :
6,9.10-7 Donc M ≈ 3,5 Am2
Pour avoir un point de comparaison nous avons calculé la valeur du moment magnétique à partir des données du constructeur. Nous avons utilisé des aimants au néodyme S-25-07-N de chez Supermagnete.com. Le champ magnétique rémanent moyen fourni par le constructeur est Br = 1,3 T Il est lié au moment magnétique M par : Avec V le volume de l’aimant : 1,37.10-4 m3 On peut alors calculer le moment magnétique de l'aimant : 3,55 Am2 |
En comparant avec les données du constructeur, la valeur trouvée de l’aimantation est cohérente. Par ailleurs on retiendra que plus on s’éloigne du dipôle plus le champ magnétique diminue. De cette constatation nous pouvons en tirer que nous devons rapprocher les bobinages le plus possible des aimants afin de générer une tension maximale.
2.2 Champ magnétique créé par le rotor en rotation devant une bobine
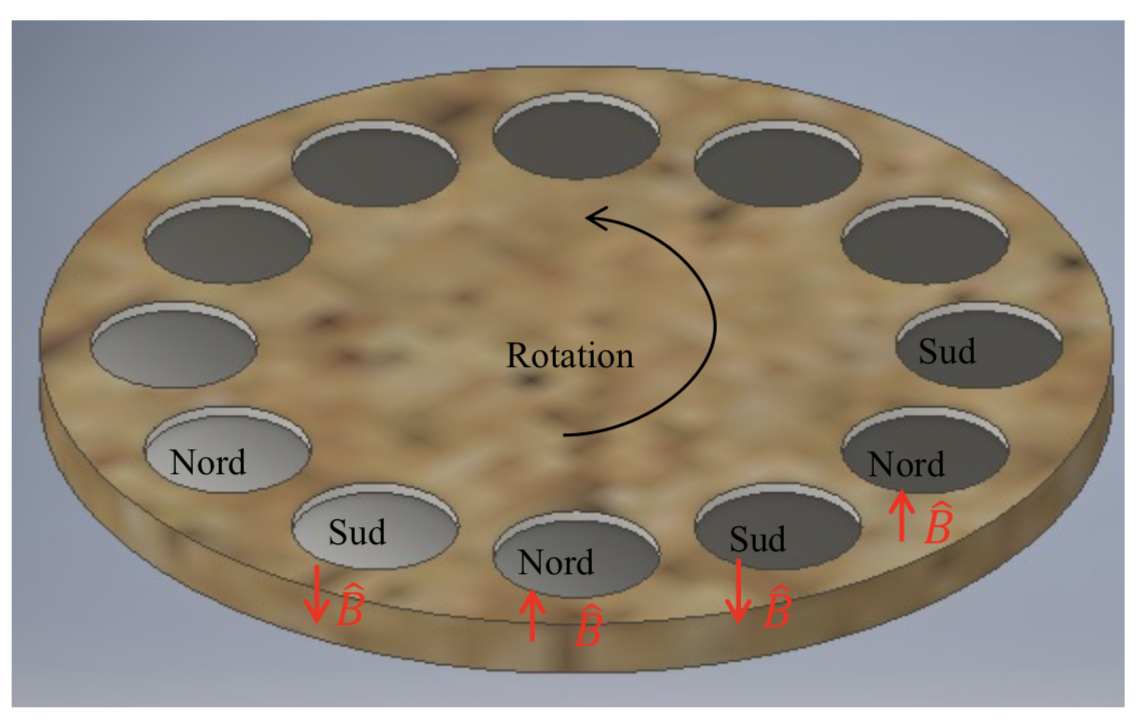
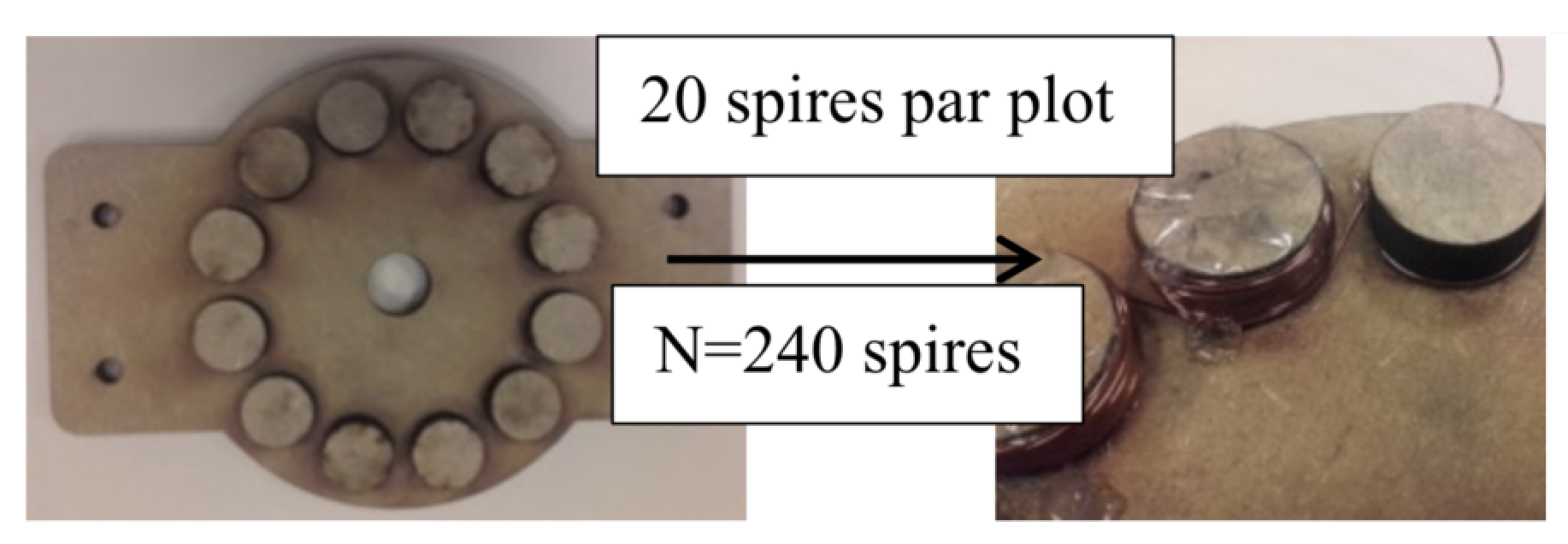
Les aimants choisis ont été mis en place sur un plateau de manière circulaire afin d’être fixés sur l’éolienne, figure 6. Afin de s'assurer que les 12 aimants étaient correctement placés et bien alternés (pôles Nord, puis Sud) nous avons mesuré le champ magnétique engendré par le plateau lorsque celui-ci est en légère rotation. Pour cela nous avons fixé un teslamètre au-dessus de l’éolienne et nous avons mis en rotation celle-ci. |
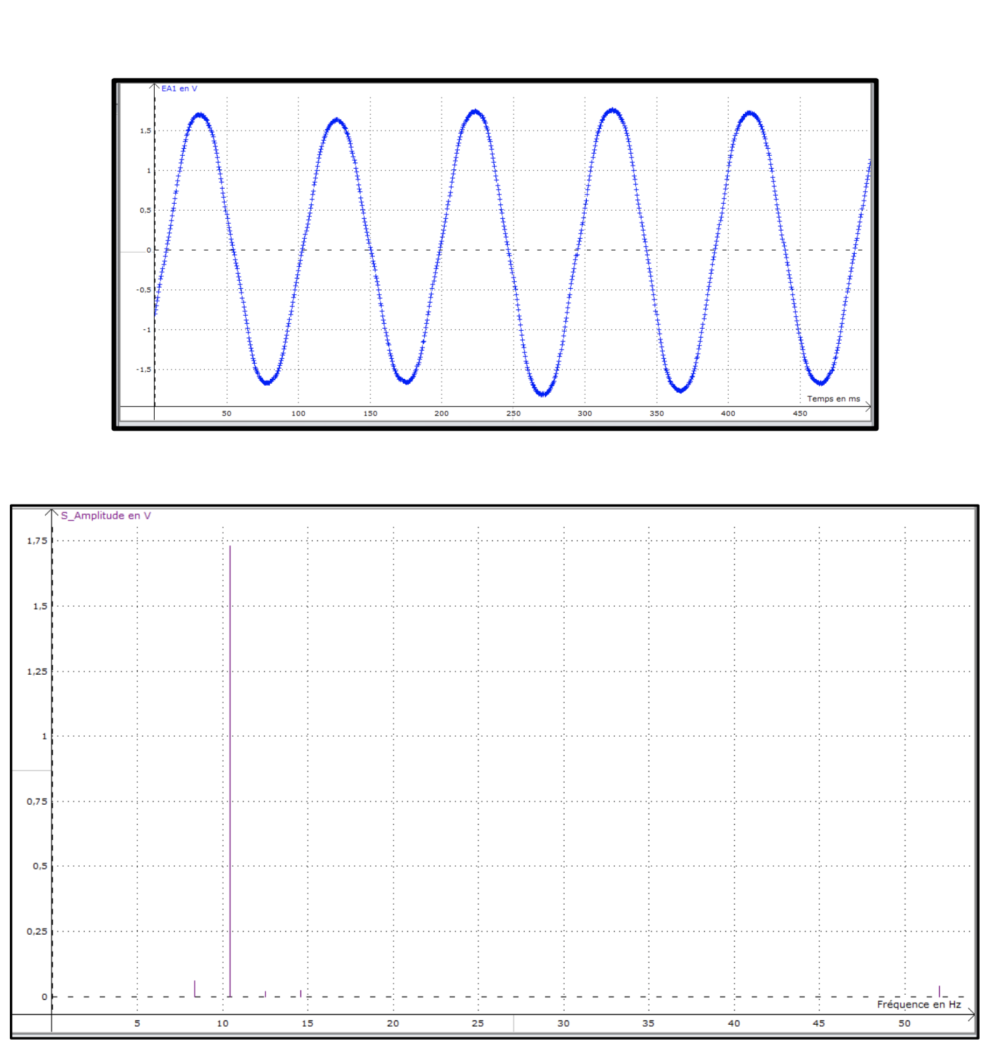
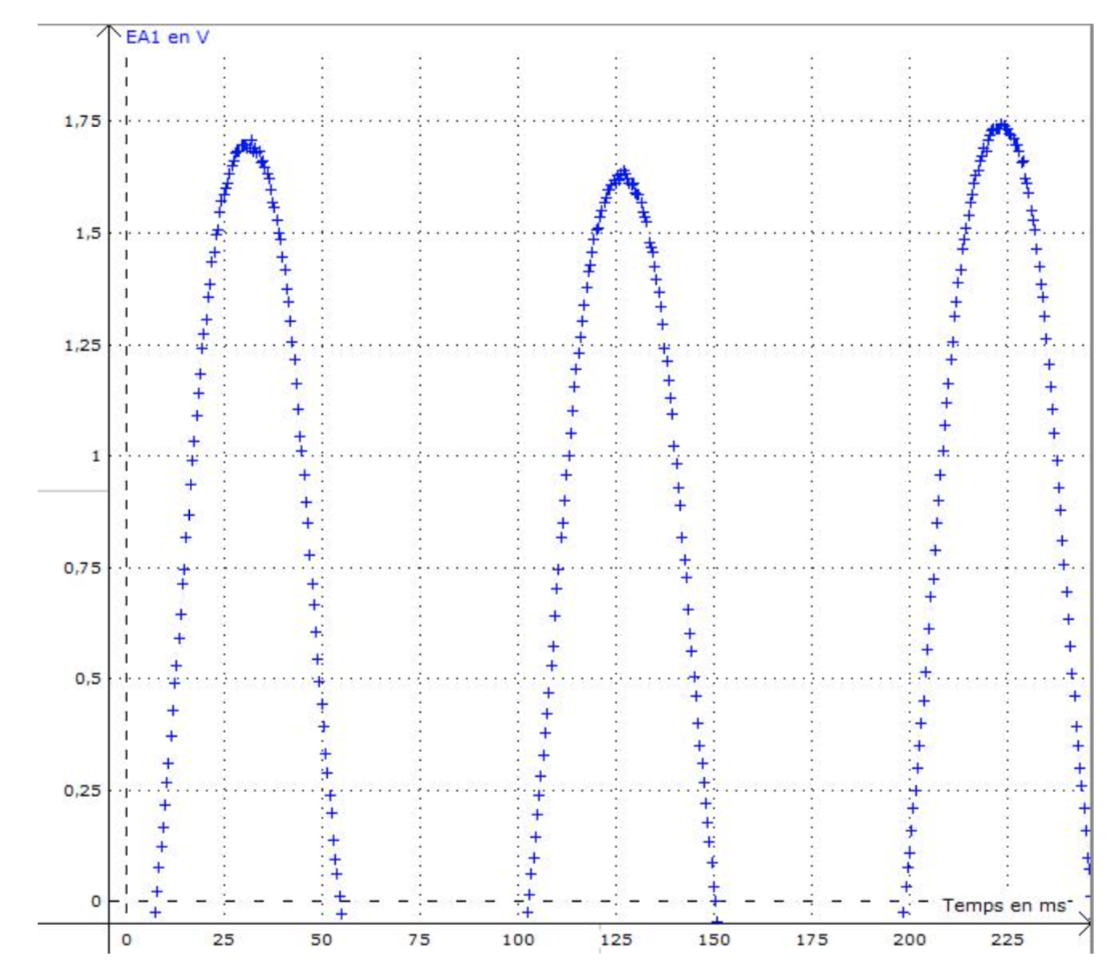
Le signal que nous avons obtenu ressemble à une sinusoïde, figures 7 et 8, cela nous permet de conclure que :
- les aimants sont donc correctement positionnés afin d’avoir une alternance de pôles Nord et de pôles Sud ;
- le champ magnétique créé est quasi-sinusoïdal.
Pour compléter l’étude nous avons tracé le spectre du champ magnétique. Celui-ci présente presque toute son énergie dans une seule raie, le signal est donc bien sinusoïdal, figure 7.
On relève Umax = 1,75 V ce qui correspond à Bmax = 175 mT.
Il est alors possible de modéliser le champ magnétique créé par la fonction mathématique :
| est la pulsation du champ magnétique (rad.s-1) ; est la vitesse angulaire du disque (rad.s-1) ; est la fréquence du champ magnétique (Hz) ; est la fréquence de rotation du disque (tr.s-1) ; est le nombre de paires de pôles (Nord-Sud) sachant qu'ici, on a N = 12 aimants |
Finalement on a : avec = 175 mT
Cette alternance des pôles est primordiale car c’est elle qui assure la variation du champ magnétique nécessaire pour induire des courants dans un circuit électrique qui sera le stator (partie statique) de notre générateur.
3. Réalisation des bobinages statoriques
3.1 Évaluation du nombre de spires
On cherche le nombre de spires nécessaire à l’obtention d’une tension de sortie efficace de 9 V pour une fréquence de rotation de l'éolienne de 16 tr.s-1 (ce qui correspond à une vitesse de vent de 6,4 m/s).
Pour calculer le nombre de spires nous avons utilisé la Loi de Lenz-Faraday qui exprime la tension générée aux bornes d’une bobine lorsque le champ magnétique qui la traverse varie :
est la tension générée par induction (force électromotrice induite) et le flux du champ magnétique à travers le bobinage tel que : où est est le nombre de spires et la section de la bobine.
Nous avons vu que notre rotor générait un champ magnétique :
Avec 6 paires de pôles, n la fréquence de rotation et Bmax ≈ 175 mT (valeur du champ magnétique à quelques millimètres de l'aimant).
On a donc :
3.2 Calcul de la résistance du bobinage
Lors de notre première expérimentation nous avions rencontré un problème avec la résistance électrique de la génératrice. Pour être sûr de ne pas être à nouveau confronté à ce problème nous avons tout d’abord calculé puis mesuré la résistance du bobinage.
La résistance électrique d’un conducteur cylindrique se calcule par la formule suivante :
Avec la résistivité du cuivre, 1,7.10-8 Ω.m, L la longueur et S la section du conducteur.
La section du conducteur est (0,3.10-3)2 = 2,82.10-7 m2
La longueur de fil est L = nombre de plots × nombre de spires par plot × 2π × rayon d'un plot = 12 × 20 × 2π × 13.10-3 = 19,6 m.
Nous aurons donc une résistance totale : 1,7.10-8 = 1,7 Ω
3.3 Réalisation des bobines
Nous avons réalisé le bobinage, figure 9. Nous avons disposé 12 plots bobinés dans la même configuration que les aimants. Les plots sont reliés en série.
Figure 9. Réalisation du bobinage |
3.4 Mesure de la résistance induite
Afin de vérifier les valeurs théoriques, nous avons mesuré à l’ohmmètre une résistance de 1,36 Ω ce qui est très proche de la valeur théorique. La résistance totale sera un peu plus élevée compte tenu des soudures et raccordements.
4. tension générées
4.1 Mesure de la tension générée et comparaison avec la prédiction théorique
Nous avons effectué une mesure de la tension induite afin de la comparer aux prédictions théoriques. La valeur obtenue, pour une vitesse de rotation de 16 tr.s-1 soit une vitesse de vent de 6,4 m/s, est de 6 V efficace environ, ce qui ne correspond pas au 9 V efficace attendu au début du dimensionnement.
Pourquoi existe-t-il un tel écart ?
4.2 Analyse des différences entre valeur théorique et valeur réelle de la tension générée
Influence du nombre d'aimants
Le dimensionnement (calcul du nombre de spires) ayant été effectué à partir de l’étude du champ magnétique créé par un seul aimant nous nous sommes demandé quelle influence a la juxtaposition des aimants sur l’amplitude du champ magnétique créé par l’ensemble des aimants.
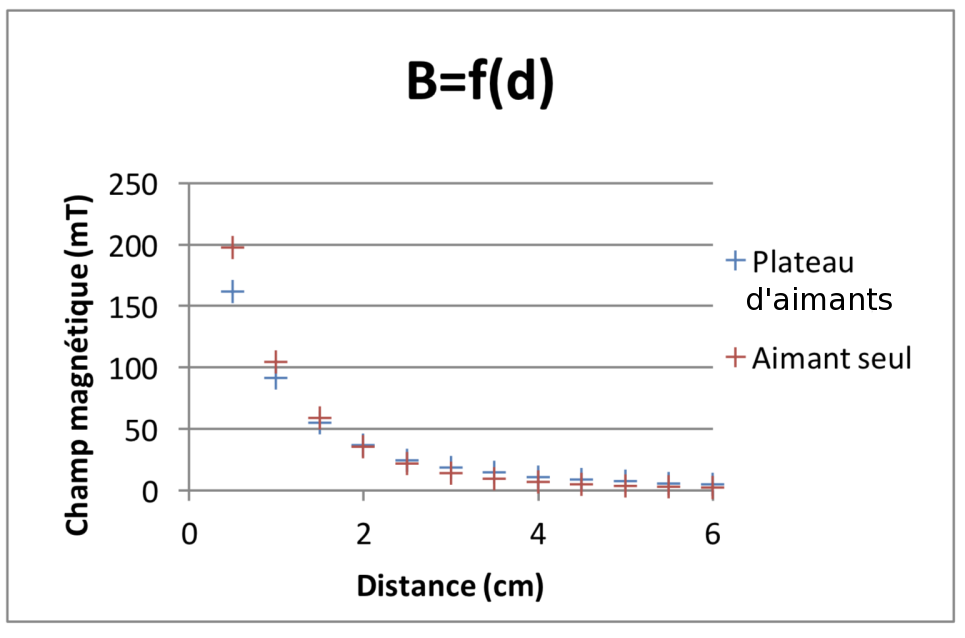
Pour mettre en évidence cet effet, nous avons mesuré le champ magnétique en fonction de la distance dans l’axe d’un des aimants du plateau, figure 10.
En comparant avec l’étude réalisée pour un seul aimant, on constate que le champ magnétique est plus faible lorsque les aimants sont côte à côte, en particulier à très faible distance, cas de notre étude. Cela explique en partie la différence obtenue entre la tension générée expérimentale et la prévision théorique, figure 11.
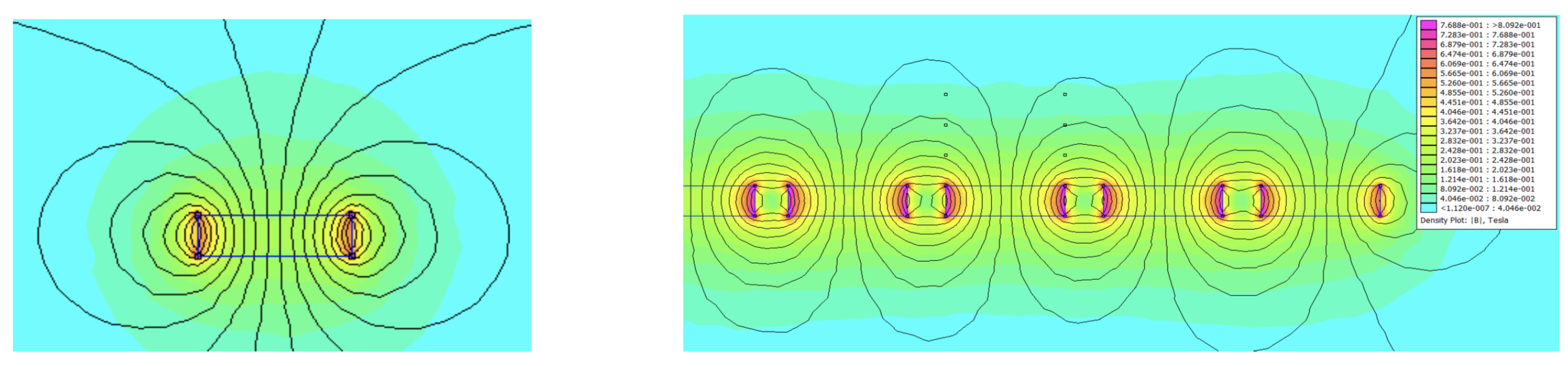
Cela se vérifie aussi par simulation numérique où l’on constate qu’à distance équivalente le champ magnétique est plus faible pour les aimants côte à côte, figure 12.
Influence de la hauteur des bobines
D’autre part nous avons pensé que les écarts observés étaient peut-être dûs aussi au fait que nous n’avions pas tenu compte de la hauteur du bobinage lors du dimensionnement et donc de la diminution du champ magnétique en fonction de la distance.
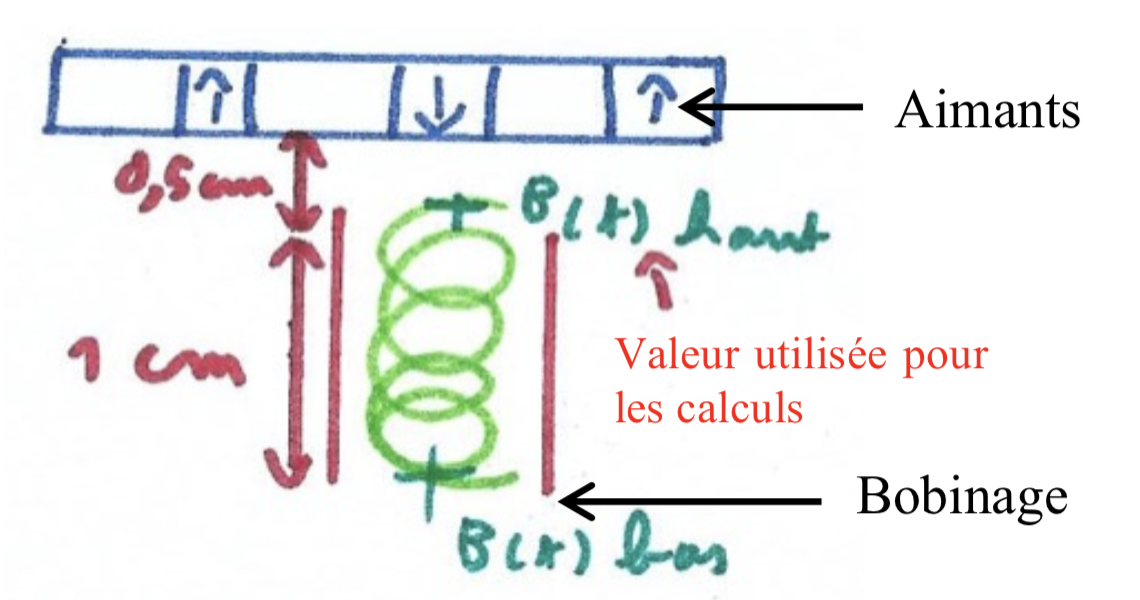
Comme le montre le schéma, figure 13, la distance aux aimants n’est pas la même en haut et en bas du bobinage. Or nous avons vu précédemment que le champ magnétique est fonction de la distance aux aimants.
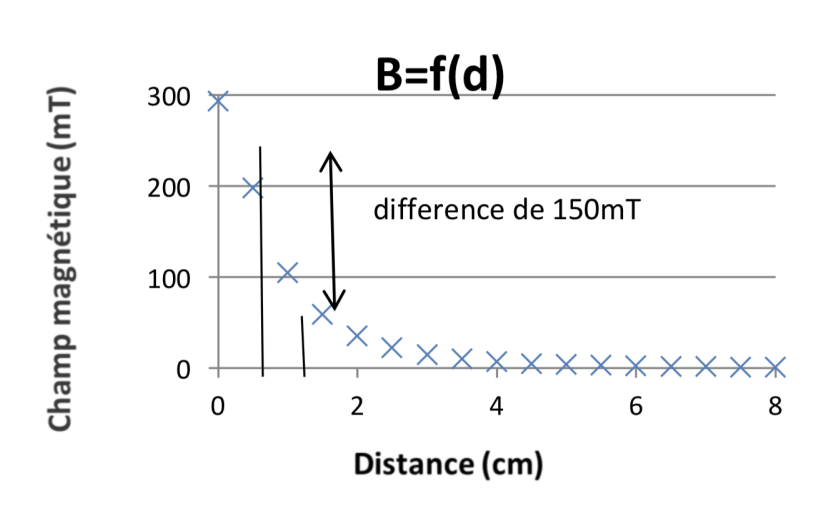
Donc la tension générée par les spires du haut est différente de celle générée par les spires du bas. Sur le graphique, figure 14, on constate une différence de 150 mT entre les deux extrema ce qui peut justifier les écarts entre valeur théorique et valeur mesurée. Pour obtenir un résultat plus proche de la réalité nous aurions pu utiliser la valeur du champ magnétique moyen soit : Bmoy = Bhaut + Bbas / 2
Répartition du champ non uniforme sur la surface des spires
Un autre point qui n’a pas été pris en compte est l’évasement des lignes de champ. Comme le montre le schéma, figure 15, le champ magnétique n’a pas la même valeur sur toute la surface de la bobine.
Nous avons aussi analysé les simulations numériques pour voir l’évolution de l’amplitude du champ magnétique tout le long de la surface de l'aimant et pour différentes distances à l'aimant, figure 16.
On constate que le champ magnétique n’est pas uniforme sur toute la surface embrassée par les spires. On retrouve que plus on s'éloigne, plus la valeur du champ diminue.
Conclusion : influence de la distance bobinages-aimant
En conclusion, nous avons fait varier la distance des bobinages et mesuré la tension générée sur le dispositif complet, figure 17.
On illustre ainsi la grande dépendance entre la distance des bobinages et la tension induite générée.
Conclusion et évolution du protoype
En conclusion, pour minimiser les effets de la distance entre les aimants et les spires du bobinage, nous avons essayé de minimiser l’espacement entre le stator (bobines) et le rotor (aimants) sans que cela génère des frottements. Celui-ci est ajusté afin d’être de l’ordre de quelques millimètres.
Finalement, pour obtenir une tension induite plus élevée, nous avons aussi choisi d'augmenter le nombre de spires en réalisant un deuxième bobinage, figure 18.
Nous avons mesuré la tension induite aux bornes des bobinages à l'aide d'un oscilloscope, figure 19. Pour une fréquence de rotation, ici d’environ 2,6 tr.s-1, les deux bobinages (jaune) fournissent une tension environ double de la tension fournie par un seul bobinage (vert), ce qui est cohérent avec le nombre de spires.
Avec le deuxième bobinage, placé en série avec le premier, la résistance totale est de 2,8 Ω ce qui reste relativement peu élevé et relativement proche de la valeur théorique. Les valeurs expérimentales sont plus élevées en raison des soudures et de la connectique. Nous pouvons tirer de cette mesure que les pertes par effet Joule dans les bobines seront limitées.
Avec les deux bobinages en série, pour une fréquence de rotation de 16 tr.s-1 (vitesse de vent de 6,4 m/s), on retrouve bien une tension de 9 V efficace.
Lire l'article : L’éolienne a le vent en poupe - Caractérisation d'une éolienne de Savonius - rendement
Pour citer cet article :
L’éolienne a le vent en poupe ! - Construction et caractérisation d'une éolienne de Savonius, Sébastien Chéry, Nino Morvan-Heckel, octobre 2020. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/eolienne-olympiades2.xml