Activer le mode zen
Ressource au format PDF
Classification
L’éolienne a le vent en poupe !
Caractérisation d'une éolienne de Savonius - rendement
05/10/2020
Travail réalisé dans le cadre des XXVIIe Olympiades de Physique sous la tutelle de Romain Dardevet, professeur de Physique-Chimie.
Résumé
Qui n’a jamais été étonné de voir une éolienne tourner dès que le vent se lève ? Celle-ci convertit par sa rotation l’énergie cinétique du vent en électricité.
Se soulèvent alors quelques questions : quelle énergie peut être récupérée de cette rotation ? Quelles données physiques peuvent-être étudiées ? Comment est produite l’énergie électrique des éoliennes ?
Dans le cadre de ce projet nous avons choisi d'étudier le modèle d’éolienne Savonius hélicoïdal qui de par sa forme et ses dimensions permet une analyse dans des souffleries en laboratoire plus aisée. Tout d’abord nous avons élaboré un protocole afin d’établir un rendement, puis nous avons souhaité produire un alternateur artisanal afin de bien comprendre la physique en jeu.
Table des matières
Ce travail fait l'objet de deux articles. Dans le premier, on présente l'éolienne de Savonius et la caractérisation d'un prototype expérimental. Dans le deuxième article, on s'intéresse à la fabrication complète (rotor et stator) de l'éolienne étudiée. Lire le deuxième article : L’éolienne a le vent en poupe - Construction d'une éolienne de Savonius
1. Description de l'éolienne
1.1 Éolienne Savonius
Sigurd Savonius (1884-1931) était un architecte et un inventeur finlandais (figure 1). C’est en observant un bateau propulsé par de gros cylindres verticaux en rotation (Buckau) que lui est venue l’idée en 1924 de l'invention de l’éolienne verticale Savonius (figures 2 et 3).
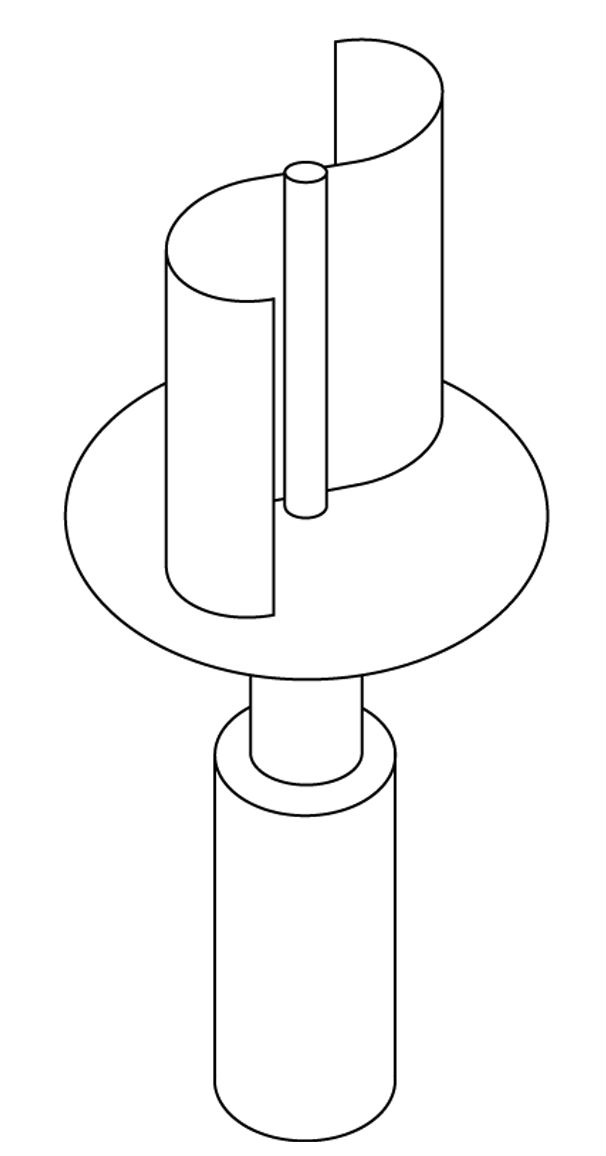
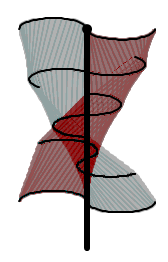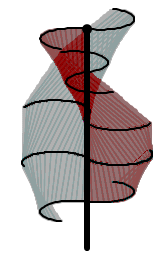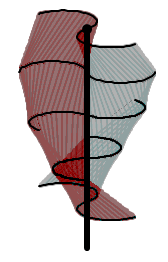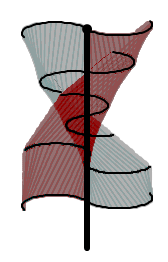
L’éolienne Savonius est constituée schématiquement de deux ou plusieurs godets demi-cylindriques légèrement désaxés. Son faible encombrement lui permet d’être facilement inséré sur les bâtiments. Il existe aujourd’hui différents types d’éoliennes Savonius comme par exemple l’éolienne Savonius hélicoïdale qui fait l’objet de notre étude (figure 7).
Figure 2. Rotor de Savonius (Source Wikimedia) | Figure 3. Éolienne de Savonius (Source UVED) |
1.2 Fonctionnement
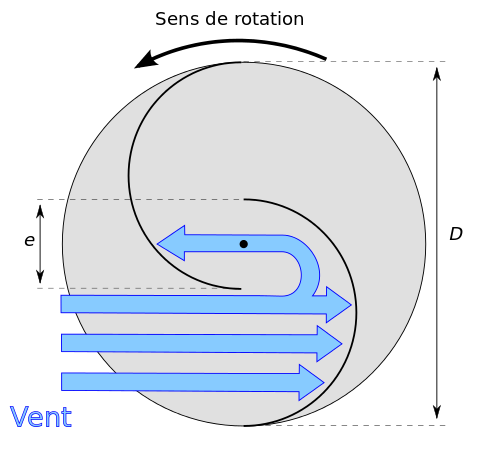
L'éolienne de Savonius fonctionne sur le principe de la traînée différentielle : la partie convexe présente une force de traînée (force s’opposant au mouvement du vent) inférieure à la force de traînée de la partie concave. Cette différence entre les forces crée un couple qui met en rotation l’éolienne, figures 4 et 5.
L’espace laissé entre les deux demi-cercles permet de laisser s’insérer un filet d’air afin de faciliter la rotation de l’éolienne et d’améliorer son rendement. L’espace optimal entre les godets doit être de 1/6 du diamètre de l’éolienne, figure 6.
1.3 Savonius hélicoïdale
Ce type d’éolienne (figures 7 et 8) est une amélioration de l’éolienne Savonius : elle repose hélicoïdalement autour de l'axe de rotation. Cela permet d'avoir une meilleure prise au vent, de façon continue en fonction de l’angle de rotation pour augmenter le rendement de l’éolienne.
1.4 Limite de Betz
Albert Betz, un physicien allemand, a montré en 1919 que la puissance mécanique maximale pouvant être récupérée par une éolienne est limitée.
La masse d’air traversant le rotor d’une turbine éolienne à axe horizontal fonctionnant en milieu ouvert, dispose d’une énergie cinétique dépendant de la surface captée par l'éolienne, de la vitesse du vent et de la masse volumique de l'air.
La puissance cinétique incidente du vent qui traverse l'éolienne s'écrit :
Avec ρ la masse volumique de l’air, S la surface balayée par le rotor et v1 la vitesse du vent en amont du rotor, figure 9.
Ce flux exerce alors une pression sur les pales du rotor qui entraînent ce dernier dans un mouvement de rotation, créant ainsi un couple moteur au niveau de l’arbre de transmission horizontal.
La vitesse du vent en sortie de turbine, v2 ne peut pas être nulle, ainsi l’énergie cinétique ne peut pas être entièrement récupérée.
La puissance développée par l'éolienne s'écrit (en considérant un écoulement stationnaire où l'air est un fluide incompressible), en étudiant une ligne de courant et en appliquant le théorème de Bernoulli :
Il y a une compétition entre deux phénomènes opposés : l'éolienne récupère d'autant plus d'énergie qu'elle freine plus le vent (ce qui est traduit par le terme (v12 − v22 )), mais elle en récupère d'autant moins que le débit est plus faible, or le ralentissement réduit le débit (ce qui est traduit par le terme (v1 + v2)).
Le maximum est atteint lorsque v2 = 1/3 v1
On a alors :
Plus généralement, on note la puissance développée par l'éolienne :
Avec Cp, le coefficient de puissance, ou rendement aérodynamique, de la machine.
Betz a montré, dans le cas d’une turbine à axe horizontal fonctionnant en milieu ouvert, que la puissance utile disponible sur l’arbre moteur à l’aval du rotor ne peut pas dépasser 16/27ème (soit 59%) de la puissance mécanique maximale récupérable, il s’agit là de la valeur limite de Cp [7]. Cette loi s'applique à tous types d'éoliennes à pales.
2. Rendement énergétique
Nous allons nous intéresser ici au calcul du rendement de l'éolienne de Savonius que nous avons fabriquée. L'année précédente, pour notre T.P.E., nous avions réalisés des modèles informatiques de ce type d'éolienne. Ils ont pu être réinvestis afin de matérialiser facilement notre maquette par impression 3D. L'alternateur, couplé à l'éolienne, a été fabriqué de toutes pièces. On peut retrouver en détail le montage et sa caractérisation dans l'article : L’éolienne a le vent en poupe - Caractérisation d'une éolienne de Savonius - Construction d'une éolienne de Savonius.
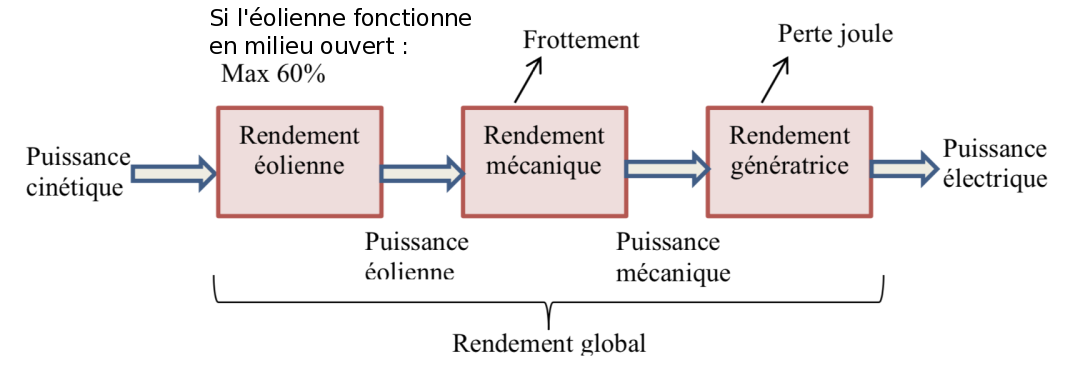
2.1 Décomposition des differents rendements
Pour réaliser le bilan énergétique, nous avons décomposé les différents rendements, figure 10.
2.2 Rendement global
Mesure de la puissance récupérée
Nous avons fait le choix d'étudier notre éolienne dans une soufflerie. La loi de Betz ne s'applique alors pas dans un canal de section constante.
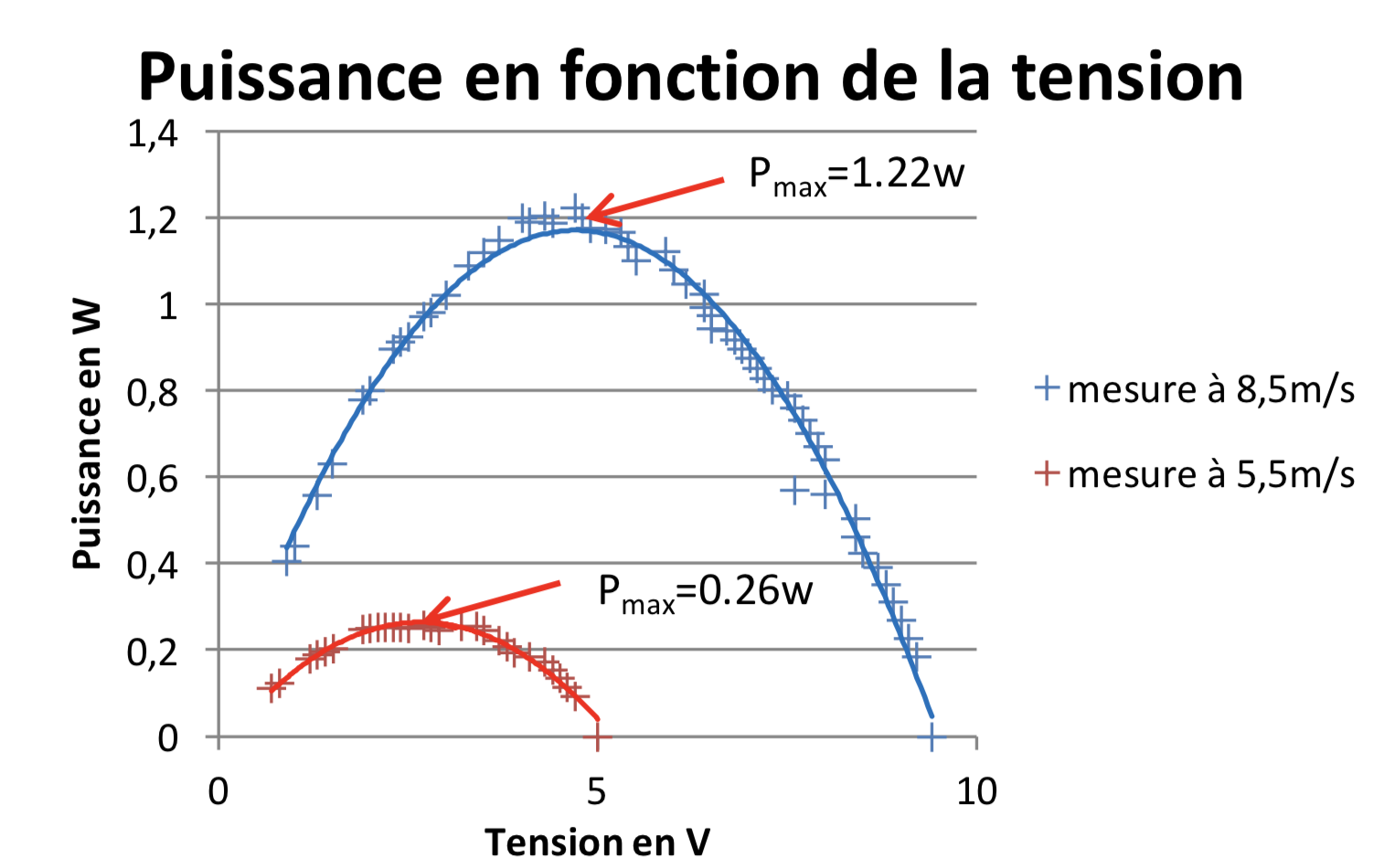
Nous avons effectué deux séries de mesures à deux vitesses de vents différentes. Le protocole est présenté figure 11. La mesure de la puissance est donnée figure 12.
À l'aide des mesures nous pouvons trouver les puissances électriques maximales récupérables :
- Pour 9,5 m/s la puissance maximale est de 1,22 W
- Pour 6.5 m/s la puissance maximale est de 0,26 W
Calcul de la puissance cinétique du vent
Nous avons calculé la puissance cinétique du vent.
- Pour un vent de 9,5 m/s : ≈ 13,4 W
- Pour un vent de 6,5 m/s : ≈ 4,3 W
Calcul du rendement global
Nous en déduisons le rendement global :
- Pour un vent de 9,5 m/s : ≈ 9,1%
- Pour un vent de 6,5 m/s : ≈ 5,9%
Le rendement est faible. Ici, dans un canal fermé, nous ne sommes pas limités par la loi de Betz. On se rend compte qu'il est difficile d'obtenir un bon rendement sur un premier prototype d'éolienne créée de toutes pièces. Mais cela nous a permis de découvrir la physique et les limitations techniques mises en jeu.
2.3 Calcul du rendement de la génératrice - pertes Joules dans les bobinages
Connaissant la puissance électrique générée par l’éolienne et la résistance des bobinages, il est possible de calculer le rendement électrique de la génératrice.
- Pour un vent de 9,5 m/s, on a : ≈ 91%
- Pour un vent de 6,5 m/sn on a : ≈ 86%
3. Conclusion
Pour conclure notre étude nous pouvons dire que l’éolienne Savonius peut être une des solutions envisagées pour permettre la transition énergétique en particulier dans les applications domestiques. Nous avons constaté qu’elle s’insérait facilement dans un petit espace, d'autres essais nous ont permis de voir que plus l’éolienne est grande plus elle génère d’énergie.
Remerciements
Nous tenions à remercier monsieur Dardevet qui nous a suivi tout au long de notre projet. Nous voulions aussi remercier Madame Mathieu qui nous a proposé de participer initialement aux défis de la physique pour le XXIème siècle. Enfin nous remercions le personnel du lycée qui nous a rendu possible l’accès aux installations techniques et aux laboratoires du lycée.
Réréfences
- [1] Futura-sciences, Quels sont les types d'éoliennes ?, https://www.futura-sciences.com/planete/questions- reponses/energie-renouvelable-sont-types-eoliennes-1226/
- [2] COURTY, Jean-Michel, KIERLIK, Edouard, Les éoliennes verticales, Pour la science (N°440), Juin 2014, p.84-86.
- [3] Le Comptoir Eolien, Les différents types d’éoliennes
- [4] Wikipédia , Éolienne
- [5] Fraenkel, P.L., Les machines élévatoires
- [6] Enerlice, Tout savoir sur l’éolienne Savonius
- [7] Énergie électrique : génération éolienne - ENS Paris-Saclay
- [8] Wikipédia , Rotor de Savonius
- [9] EM6 : Dipôle magnétique
- [10] Jancovici , Pourrait-on alimenter la France en électricité uniquement avec de l’éolien ?
- [11] F4jr , Étude théorique d'une éolienne
- [12] odpf , Dans le vent !
- [13] Ces , eduparck [logiciel] version 2013 disponible sur les ordinateur du lycée
- [14] Wikipédia , Sigurd Savonius
- [15] Winside
Pour citer cet article :
L’éolienne a le vent en poupe ! - Caractérisation d'une éolienne de Savonius - rendement, Sébastien Chéry, Nino Morvan-Heckel, octobre 2020. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/eolienne-olympiades1.xml