Activer le mode zen
Ressource au format PDF
Mots-clés
- numérique
- conversion
- analogique
- quantification
- convertisseur d'énergie
- expérience
- critère de Shannon
- échantillonneur-bloqueur
- bit
- échantillonnage
Classification
Comment convertir un signal analogique en signal numérique au laboratoire
29/06/2012
Résumé
Cet article détaille de façon expérimentale les étapes qui permettent la conversion analogique numérique au laboratoire.
Dans la première partie de l'article, on explique le fonctionnement du convertisseur qui reçoit en entrée un signal analogique continu pour le convertir en sortie en un signal numérique composé d'une succession de 0 et de 1 (voir l'article précédent : « Principe du passage de l'analogique au numérique »). Puis dans une deuxième partie, on convertit un signal sinusoïdal délivré par un générateur. Cette opération permet de détailler le choix des paramètres vu dans l'article précédent et notamment le choix de la fréquence d'échantillonnage et ses effets sur le signal de sortie.
Un article du dossier « Traitement du signal ».
Table des matières
Convertisseur analogique-numérique
L'objectif de cette partie est de montrer comment un signal analogique que l'on choisit ici continu peut être numérisé sur 3 bits.
Présentation
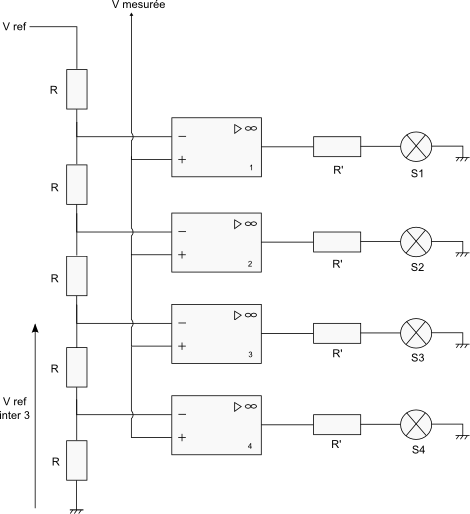
Le convertisseur utilisé est un convertisseur parallèle (flash). Il est constitué de 4 amplificateurs opérationnels (boitier TL084) montés en comparateur. L'amplificateur opérationnel possède deux entrées : V+ et V-. La sortie du comparateur affiche une tension égale à +15 V si V+ > V-, et -15 V sinon.
On applique sur l'entrée V+ le signal à convertir (Vmesurée) et sur l'entrée V- la valeur de référence qui sert à la comparaison.
A la sortie des comparateurs, des diodes électroluminescentes s'allument si la sortie du comparateur indique +15 V ce qui permet rapidement de savoir si Vmesurée > V+.
Figure 1. Schéma du convertisseur analogique-numérique utilisé pour cette expérience
Figure 2. Convertisseur analogique-numérique utilisé pour l'expérience
Figure 3. Zoom sur la plaquette contenant les 4 amplificateurs opérationnels du circuit intégré TL 084
Le convertisseur utilisé possède 4 amplificateurs soit 4 niveaux de comparaison. Si la valeur de référence Vref = 5 V alors les 4 niveaux successifs intermédiaires à l'entrée V+ de l'amplificateur opérationnel sont 1 V, 2 V, 3 V et 4 V.
Exemple : Vref = 5Ri et Vref inter 3 = 2Ri d'où Vref inter 3 = (2R/5R) Vref = 2/5 Vref
Application numérique : Vref inter 3 = 2 V
Les diodes électroluminescentes s'allument si la tension de sortie du comparateur est positive soit +15 V ce qui permet de donner un encadrement de la tension mesurée. Pour connaître la valeur de la tension mesurée, il faut faire un transcodage selon le tableau suivant :
Tableau 1. Transcodage
|
S1 S2 S3 S4 |
Binaire |
Décimal | |
|---|---|---|---|
|
Vmesurée < 1V |
0 0 0 0 |
0 0 0 |
0 |
|
1V < Vmesurée < 2 V |
0 0 0 1 |
0 0 1 |
1 |
|
2V < Vmesurée < 3 V |
0 0 1 1 |
0 1 0 |
2 |
|
3V < Vmesurée < 4 V |
0 1 1 1 |
0 1 1 |
3 |
|
4V < Vmesurée < 5 V |
1 1 1 1 |
1 0 0 |
4 |
Exemple : Si la diode S4 s'allume (S4 = 1), la tension en sortie du comparateur est donc positive ce qui signifie que l'entrée V+, Vmesurée, est supérieure à l'entrée V- : Vmesurée > 2 V (niveau de comparaison du comparateur 4). Et si la diode S3 reste éteinte, alors Vmesurée < 4 V. Ce résultat permet donc de déterminer un encadrement de Vmesurée.
Dans le cas présent, le codage s'effectue sur 3 bits, limitant ainsi la précision. Plus le nombre de bits sera grand, plus le nombre de niveaux successifs augmentent et meilleur est l'encadrement.
Tests au laboratoire
Le signal mesuré est un signal continu qui est envoyé à l'entrée positive de l'amplificateur opérationnel. L'éclairement des diodes électroluminescentes permet de déduire l'encadrement de la tension mesurée.
Dans l'exemple de la figure 2, les diodes S3 et S4 sont allumées. Si on se réfère au tableau précédent, ceci indique que la tension mesurée est comprise entre 2 et 3 V. Un voltmètre placé aux bornes du générateur indique la tension mesurée et l'on peut lire Vmesurée = 2,07 V.
Un autre exemple figure 4 montre que les diodes S2, S3 et S4 sont allumées ce qui donne l'encadrement de la tension entre 3 et 4 V. Le voltmètre indique Vmesurée = 3,16 V.
Figure 4. Convertisseur analogique-numérique Vmesurée = 3,16 V
Ces deux exemples permettent d'illustrer le principe de la conversion analogique–numérique. Le signal à mesurer est discrétisé grâce aux différents niveaux de comparaison indiqués par les diodes.
Après avoir détaillé la discrétisation, nous allons dans la partie suivante mettre en oeuvre l'échantillonnage d'un signal sinusoïdal.
Echantillonnage
Dans le cas d'un signal variable tel qu'un signal sinusoïdal la tension mesurée varie au cours du temps. Il faut en amont échantillonner (cf article précédent) le signal afin que la tension à mesurer soit comparée à des intervalles de temps régulier. On utilise pour cela un échantillonneur-bloqueur.
L’échantillonneur-bloqueur est un montage électronique permettant de prélever aux instants d’échantillonnage nTe la valeur X(nTe) du signal continu x(t) et de maintenir cette valeur jusqu’à l’instant (n+1)Te.
Cette fonction est assurée ici par un circuit intégré : AD 781
Une entrée est réservée au signal à échantillonner et une seconde entrée permet d'envoyer un signal TTL dont la fréquence correspond à la fréquence choisie pour l'échantillonnage. (cf article précedent choix de la fréquence).
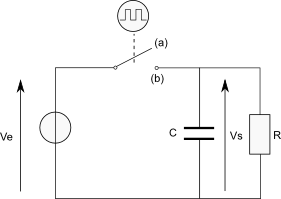
Un échantillonneur-bloqueur peut être réalisé au laboratoire à l'aide d'un interrupteur commandé (4066) par un signal TTL c'est à dire un signal carré qui prend deux valeurs : 0 V et 5 V, dit signal d'horloge, d'un condensateur et une résistance en parallèle.
Le signal que l'on échantillonne est un signal de la forme avec f = 1 kHz.
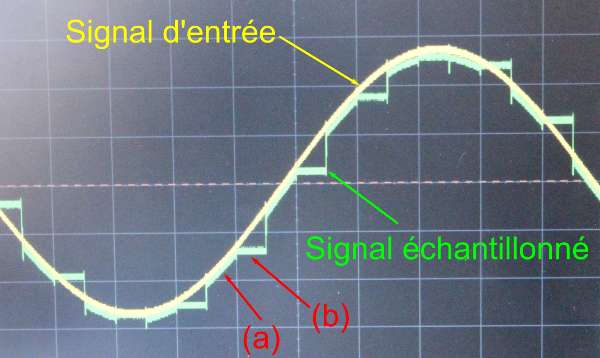
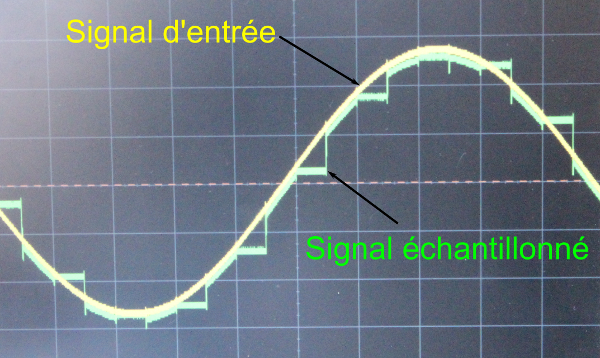
Figure 6. Signal d'entrée et signal échantillonné
Remarque : La constante de temps τ = RC est choisie suffisamment grande par rapport à la période d'échantillonnage pour que le condensateur n'ait pas le temps de se décharger.
Choix du rapport cyclique
Le réglage de la fréquence d'échantillonnage se fait par l'intermédiaire d'un signal TTL. La fréquence de ce signal correspond à la fréquence d'échantillonnage.
Le signal carré prend une valeur haute 5 V pendant T/2 puis une valeur basse pendant T/2 et ainsi de suite. Sur certains générateurs de tension, le rapport entre le temps haut et le temps bas peut varier et peut être réglé par l'utilisateur. On parle de rapport cyclique.
Voici trois exemples de signaux en sortie de l'échantillonneur-bloqueur avec des signaux TTL de rapport cyclique différents :
On remarque que le rapport cyclique modifie le temps de blocage de l'échantillonneur-bloqueur mais ne modifie pas la fréquence à laquelle sont choisis les échantillons.
Dans la pratique, on choisit généralement un rapport cyclique faible afin de tendre vers un signal impulsionnel.
Effet de la fréquence d'échantillonnage
On cherche maintenant à étudier l'effet de la fréquence d'échantillonnage pour la reconstruction future du signal. Le signal d'entrée est un signal sinusoïdal de fréquence 1 kHz. Le critère de Shannon (voir l'article précédent : « Principe du passage de l'analogique au numérique ») nous indique que la fréquence d'échantillonnage doit être supérieure à 2 fois la fréquence maximale du signal soit fe > 2 kHz
Dans le cas où le signal d'entrée est connu et est composé que d'une fréquence, le choix de la fréquence d'échantillonnage est aisé puisque le critère de Shannon s'applique directement. Lorsque le signal à traiter est plus riche en harmoniques, des opérations de filtrage du signal en amont sont nécessaires pour fixer la fréquence maximale du signal que l'on souhaite traiter. On étudie ici un cas simplifié pour illustrer la technique.
Les 4 fréquences d'échantillonnage testées sont 20 kHz, 10 kHz, 1,2 kHz et 800 Hz.
Cas où le critère de Shannon est respecté
Source - © 2012 M. Glénat et D. Chareyron
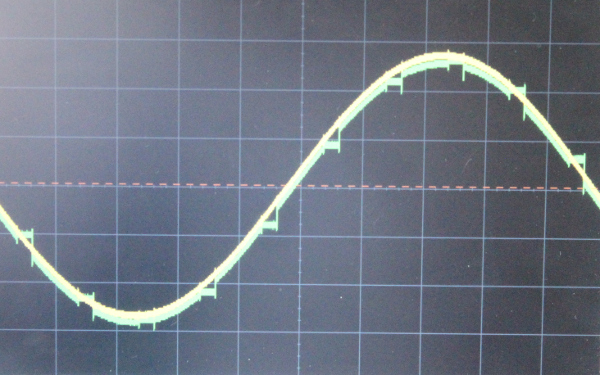
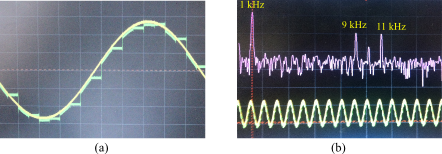
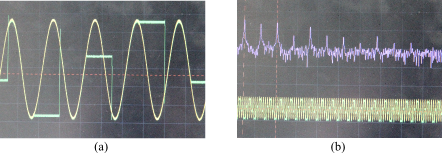
(a) Représentation temporelle : Signal jaune : signal d'entrée Ve ; Signal vert : signal de sortie Vs
(b) Représentation fréquentielle : Pic principal à 1 kHz ; largeur de la fenêtre à l'écran : 16 kHz
Les pics que l'on observe à 9 kHz et 11 kHz correspondent aux fréquences centrées autour de fe (fe-f et fe+f) (voir l'article précédent : « Principe du passage de l'analogique au numérique »)..Une opération de filtrage passe bas est réalisée pour ne conserver que les fréquences représentatives du signal. Les fréquences introduites lors de l'opération d'échantillonnage sont supprimées.
Figure 12. Fréquence d'échantillonnage 10 kHz
Source - © 2012 M. Glénat et D. Chareyron
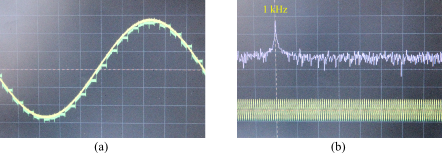
(a) Représentation temporelle : Signal jaune : signal d'entrée Ve ; Signal vert : signal de sortie Vs ;
(b) Représentation fréquentielle : Pic principal à 1 kHz ; largeur de la fenêtre à l'écran : 5 kHz
Les fréquences centrées autour de fe existent mais n'apparaissent pas dans la largeur de la fenêtre choisie.
Figure 13. Fréquence d'échantillonnage 20 kHz
Pour les fréquences égales à 10 et 20 kHz, le critère de Shannon est parfaitement respecté.
En temporel, on remarque que le signal de sortie (vert) suit bien le signal d'entrée (jaune). Une étape supplémentaire de lissage du signal permettrait de retrouver parfaitement le signal d'entrée.
En fréquentiel, on voit aussi que le pic correspond à la fréquence du signal mesuré. La reconstruction connaissant la fréquence du signal est facilement réalisable.
Cas où le critère de Shannon n'est pas respecté
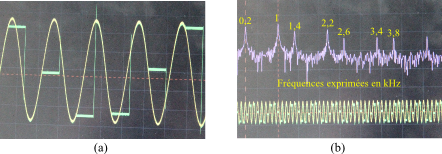
Figure 14. Fréquence d'échantillonnage 1,2 kHz
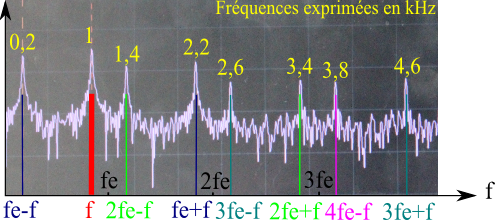
Figure 15. Zoom sur le contenu fréquentiel du signal de sortie fe = 1,2 kHz
Dans cet exemple, le phénomène de repliement de spectre apparaît (voir l'article précédent : « Principe du passage de l'analogique au numérique »).
Les résultats sont similaires pour fe = 800 Hz.
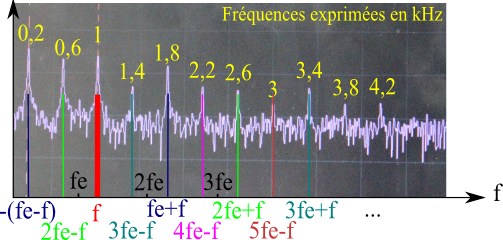
Figure 16. Fréquence d'échantillonnage fe = 800 Hz
Figure 17. Zoom sur le contenu fréquentiel du signal de sortie fe = 800 Hz
Pour les fréquences égales à 800 Hz et 1,2 kHz, les conditions du critère de Shannon ne sont plus respectées.
En temporel, le signal de sortie dans les deux cas ne suit plus le signal d'entrée. La fréquence d'échantillonnage est trop proche de la fréquence du signal et trop peu d'échantillons du signal sont prélevés.
Les conséquences sont aussi notables dans le domaine fréquentiel puisque toutes les fréquences sont mélangées. On ne reconnaît plus les fréquences du signal et les fréquences introduites lors de l'opération d'échantillonnage.
Lorsque la fréquence d'échantillonnage est trop proche de la fréquence maximale du signal, il est impossible de retrouver la fréquence fondamentale f.
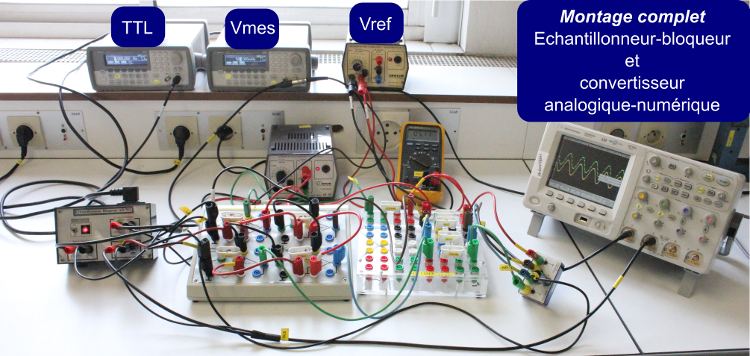
Montage complet : échantillonnage et conversion
Le montage complet du système
Figure 18. Schéma du convertisseur analogique-numérique utilisé pour cette expérience
Le fonctionnement du système complet est présenté ci-dessous en vidéo.
L'oscilloscope est réglé de façon à voir en même temps les variations de la tension et l'affichage des diodes électroluminescentes.
Article précédent : « De l'intérêt de passer dans le monde numérique ».
Dossier : « Traitement du signal ».
Pour citer cet article :
Comment convertir un signal analogique en signal numérique au laboratoire, Mathilde Glenat, Delphine Chareyron, juin 2012. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/conversion-analogique-numerique-experience.xml