Activer le mode zen
Ressource au format PDF
Classification
L'arc-en-ciel
24/01/2003
Article publié sur le site Planet-Terre par Benoît Urgelli le 15 juin 2001.
Résumé
Une explication et des images du phénomène de l'arc-en-ciel : sa forme, sa position par rapport à l'observateur, les arcs-en-ciel doubles, etc...
Table des matières
Pourquoi un arc en ciel ?
L'arc en ciel est un phénomène de dispersion de la lumière du soleil sur un mur d'eau. La lumière est réfléchie et réfractée à l'intérieur des goutelettes. L'indice n de l'eau n'étant pas le même pour les différentes couleurs composant la lumière blanche, celles-ci sont séparées à la sortie de la goutelette comme elles le sont à la sortie d'un prisme. La lumière bleue, par exemple, est préférentiellement réfléchie suivant un angle de 40,5° par rapport aux rayons du soleil, tandis que la lumière rouge est préférentiellement réfléchie suivant un angle de 42,4°.
Nous allons ici montrer comment on peut déterminer l'angle correspondant à une couleur donnée, une goutte d'eau étant modélisée par une sphère d'indice n. Puisque la taille des gouttes d'eau est très grande devant la longueur d'onde de la lumière, on peut appliquer les règles de l'optique géométrique. On obtient les trajectoires des rayons lumineux comme sur la figure. Le rayon rentre dans la goutte, est réfléchi à l'intérieur (seule une faible proportion est réfléchie, le rayon transmis ne donne lieu à aucun phénomène particulier), puis ressort.
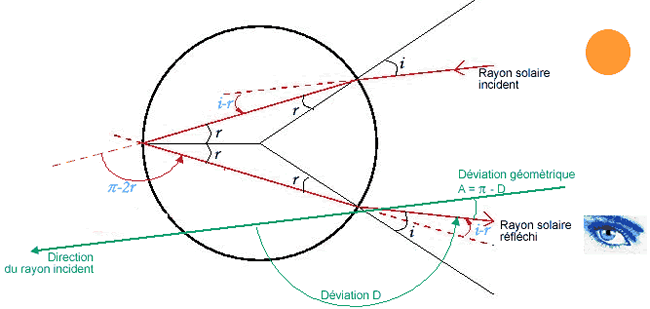
Cas d'une unique réflexion (arc-en-ciel primaire)
L'addition des angles en bleu sur la figure donne la valeur de la déviation du rayon réfléchi par rapport au rayon solaire incident. On a D= π +2i-4r, où i et r sont reliés par la loi de Descartes sin i = n sin r. La déviation dépend donc de l'angle i d'attaque du rayon, qui dépend du point d'arrivée du rayon sur la goutte. Si l'on ne travaille pas avec des angles orientés, la déviation est donnée par l'angle : A= π -D = 4 r - 2 i
L'angle non orienté i varie entre 0 et π/2, la déviation A varie donc elle aussi : il n'y a pas une seule valeur possible pour A. Cependant, toutes les valeurs de A ne sont pas équivalentes : à certaines valeurs correspond une forte intensité lumineuse, tandis qu'à d'autres est associée une intensité lumineuse nulle. La figure ci-dessous montre que A varie entre 0 et une valeur Amax d'environ 40° (que l'on peut aussi trouver par le calcul : voir la note ci-dessous), par conséquent, il n'y a pas de rayon dévié avec un angle A > Amax : l'intensité lumineuse déviée avec un angle supérieur à Amax est nulle. De plus, aux valeurs proches de Amax correspond une grande plage de valeurs de i , donc l'intensité lumineuse réfléchie dans cette direction-là sera maximale.
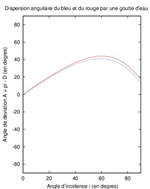
Courbes donnant A en fonction de i pour la lumière bleue (n=1,344, Amax = 40,5°) et la lumière rouge (n=1,331, Amax = 42,4°)
Pour agrandir l'image, cliquez ici.
La figure montre que la valeur de Amax dépend de n : on retrouve que l'intensité lumineuse réfléchie est maximale lorsque A = Amax = 40,5° pour la lumière bleue et lorsque A = Amax = 42,4° pour la lumière rouge.
Cette valeur maximale Amax peut être, soit déterminée graphiquement, soit calculée en dérivant la fonction A(i) = 4 r - 2 i = 4 sin-1(sin i / n) - 2 i. Elle est minimale pour cos2(i) = ((n2-1)/3).
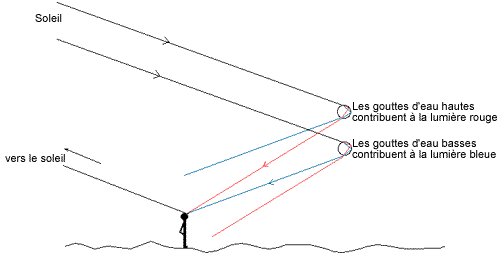
La figure ci-dessus montre que les gouttes d'eau qui envoient de la lumière vers l'observateur sous un angle de 42,4° sont plus hautes que les gouttes d'eau qui lui envoient de la lumière sous un angle de 40,5°. Par suite, la lumière venant des gouttes d'eau hautes sera plus rouge aux yeux de l'observateur que la lumière venant des gouttes d'eau les plus basses, dans laquelle le bleu dominera.
On voit donc un arc-en-ciel de couleurs, la couleur rouge se trouvant à l'extérieur de l'arc-en-ciel et la couleur bleue à l'intérieur.
La forme de l'arc-en-ciel
Ainsi, les rayons lumineux perçus par l'observateur et dans lesquels le rouge (bord externe de l'arc-en ciel) domine correspondent à l'ensemble des rayons issus du mur de pluie et faisant un angle de 42,4° avec la direction des rayons solaires (cf schéma). Les rayons lumineux constituant chaque couleur de l'arc-en-ciel forment alors des cônes de sommet les yeux de l'observateur et d'axe le rayon solaire passant par les yeux de l'observateur. L'angle entre une des génératrices du cône et son axe est alors la valeur de Amax correspondant à la longueur d'onde considérée. Cet angle a été représenté sur le schéma pour le bord externe de l'arc-en-ciel (couleur rouge) : il vaut 42,4° environ.
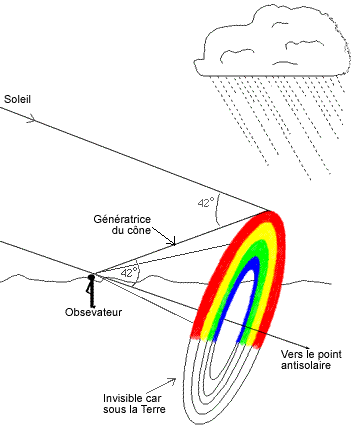
On appelle parfois "point antisolaire" le point situé à l'infini (dans la direction opposée au soleil) sur la droite passant par les yeux de l'observateur et parallèle aux rayons solaires, c'est-à-dire sur l'axe des cônes décrits ci-dessus.
Plusieurs réflexions sont possibles dans la goutte, donnant lieu au phénomène de double arc en ciel, que l'on peut observer si les conditions sont bonnes.
L'arc secondaire est moins lumineux et l'ordre des couleurs est inversé par rapport a l'arc-en-ciel primaire. La génératrice du cône correspondant à la couleur bleue (qui se trouve au voisinage du bord externe de l'arc-en-ciel) fait un angle de 53,7° avec la droite passant par les yeux de l'observateur et le point antisolaire.
Enfin la bande comprise entre les arcs primaires et secondaires s'appelle la bande sombre d'Alexandre.
La bande sombre d'Alexandre : le ciel est plus sombre à l'extérieur de l'arc-en-ciel, dans la bande sombre d'Alexandre, qu'à l'intérieur. En effet, la lumière est réfléchie dans toutes les directions comprises entre 0 et Amax. Au-dessous de l'arc-en-ciel, A < Amax : de la lumière est réfléchie dans cette direction, mais au-dessus, A > Amax , donc il n'y a pas de lumière réfléchie dans cette direction via une seule réflexion.
Une galerie d'images
Accéder à des « Images d'arc-en-ciel ».
Pour aller plus loin
Quelques activités (expérience...) sur l'arc-en-ciel sur le site de l'académie de Caen
Consulter l'ouvrage : Qu'est ce que l'optique géométrique de Luc Dettwiller chez Dunod Université (particulièrement les pages 88 à 94)
Pour citer cet article :
L'arc-en-ciel, Stéphane Peysson, janvier 2003. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/arcenciel.xml




