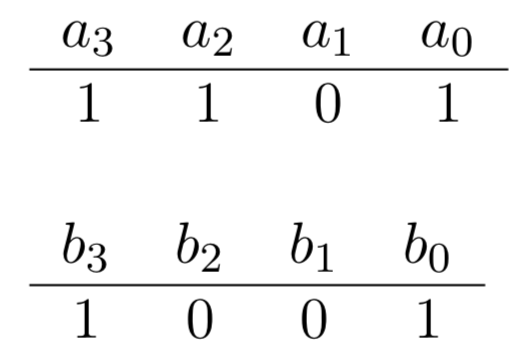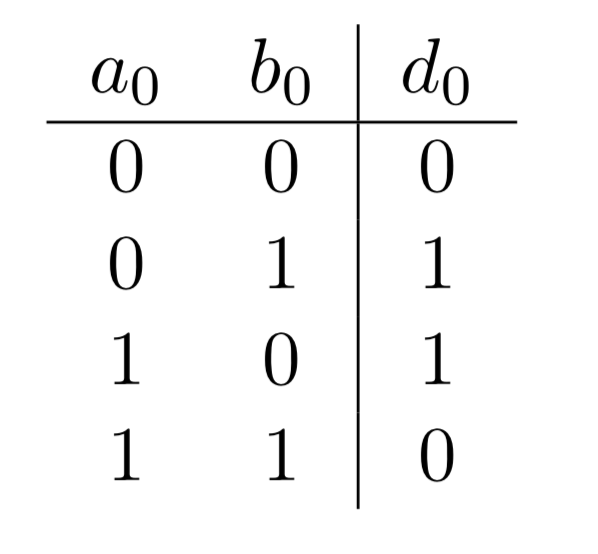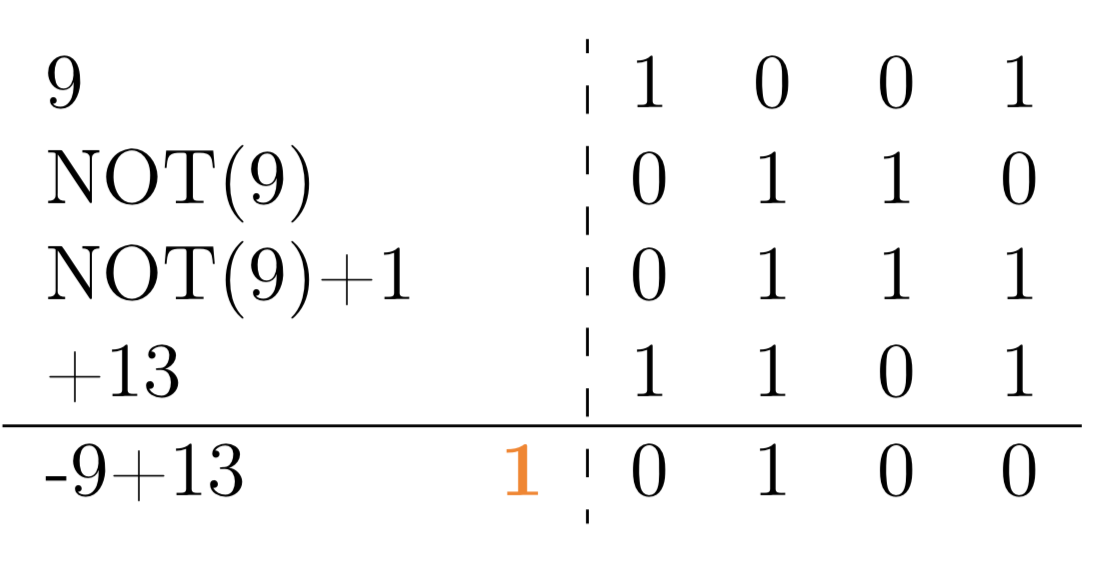Activer le mode zen
Ressource au format PDF
Mots-clés
- binaire
- numérique
- bit
- porte logique
- écoulement
Classification
TP - Fabrication d'un additionneur numérique hydraulique
21/09/2021
Résumé
Dans cet article nous présentons un additionneur binaire hydraulique facile à construire et basé sur des principes physiques simples.
Table des matières
1. Introduction
1.1 Les débuts des machines à calculer
Historiquement, après l'apparition de tables de calcul, bouliers et règles à calculer, les premières machines à calculer fonctionnaient de manière mécanique. La « Pascaline », mise au point par Blaise Pascal (vers 1645) permettait de réaliser des additions et des soustractions par un habile système de roues et d'engrenages. Une des principales caractéristiques de cette machine résidait dans son report automatique des retenues. Plus tard, en 1671, Gottfried Wihelm Leibniz perfectionna la machine de Pascal pour effectuer aussi des multiplications et des divisions.
Par la suite de nombreuses autres machines mécaniques puis électromécaniques ont été proposées. Les progrès les plus marquants reposent sur l'invention du transistor en 1947 pour lequel John Bardeen, William Shockley et Walter Brattain du laboratoire Bell ont reçu le prix Nobel. Avec la naissance du microprocesseur (circuit intégré regroupant tous les composants qui constituent un processeur), en 1971, la fréquence de calcul a augmenté considérablement. En effet, les derniers microprocesseurs possedent plus de 10 milliards de transistors intégrés et réalisent plus de 10 000 milliards d'opérations par seconde.
L'additionneur binaire hydraulique que nous présentons ici a un fonctionnement similaire aux premières machines mécaniques et son intérêt est avant tout pédagogique et non basé sur ses performances en temps de calcul.
1.2 Numération binaire
Une des taches fondamentales réalisées par un ordinateur est de résoudre des opérations arithmétiques. Ajouter des nombres binaires (\(a\) et \(b\)) n’est rien de plus qu’une routine très simple.
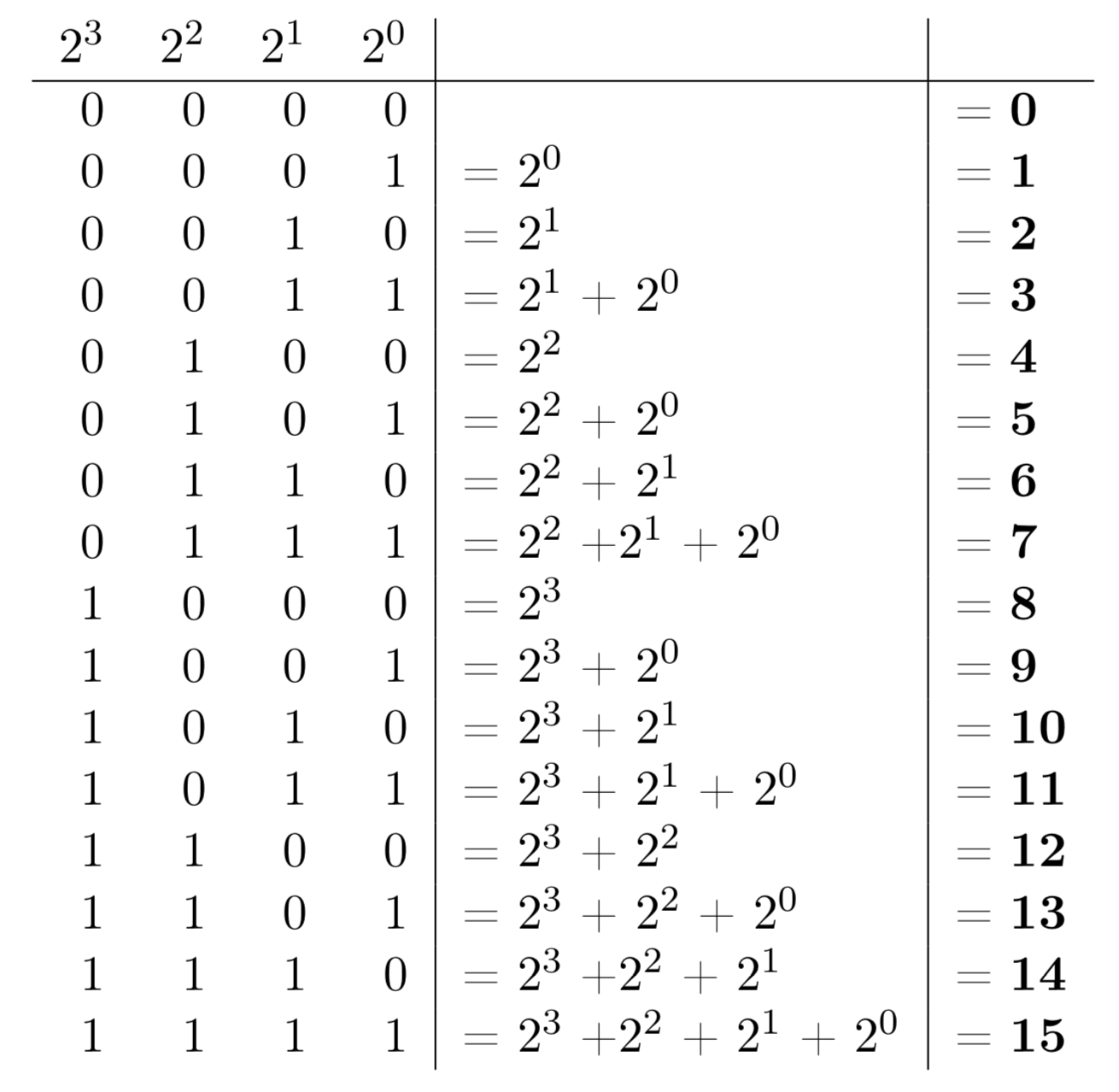
Rappelons, dans un premier temps, le principe de numération binaire. Par exemple, avec 4 bits on peut compter de 0 à 15, figure 1.
Figure 1. Numération binaire Avec 4 bits, il est possible de compter de 0 jusqu'à 15. |
2. Ajouter deux nombres binaires
2.1 Opérations logiques
Une fois le principe de numération binaire rappelé, nous pouvons maintenant effectuer une addition.
Prenons deux nombres binaires (\(a\) et \(b\)) codés sur quatre chiffres, figure 2.
L'addition de \(a\) : 1101 (= 13) avec \(b\) : 1001 (= 9) est calculée de la manière suivante, du bit de poids le plus faible \(a_0\) et \(b_0\) jusqu'au bit de poids le plus fort \(a_3\) et \(b_3\) :
- 1 plus 1 donne zéro avec une retenue de 1
- 0 plus 0 donne zéro, ce qui fait 1 avec la retenue précédente
- 1 plus 0 donne 1
- 1 plus 1 donne 0 avec une retenue de 1
Le résultat est : 10110 (= 22).
Lorsque l’on ajoute le premier chiffre de chaque nombre (\(a_0\) et \(b_0\)), on obtient le premier chiffre de leur somme (\(d_0\)) et la première retenue (\(c_0\)). La retenue est égale à 1 si et seulement si \(a_0\) = \(b_0\)=1. La somme est égale à 1 si et seulement si soit \(a_0\) soit \(b_0\) est 1 (pas les deux à la fois).
Ces opérations spécifiques pour la somme et la retenue peuvent être représentées par des fonctions logiques.
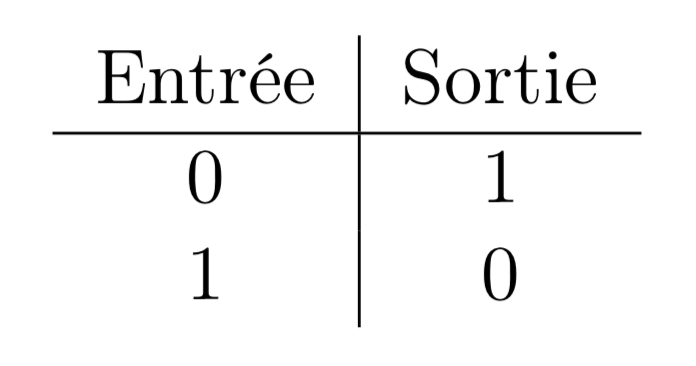
Afin de comprendre le principe des fonctions logiques, prenons un des exemples les plus simples : l'inversion logique ou fonction NOT (ou NON en français). Chaque fonction logique est définie à partir d'un tableau, appelé table de vérité, qui indique la valeur de sortie selon toutes les possibilités des valeurs d'entrée. Pour cette table, il n'y a qu'une entrée (un chiffre binaire) qui peut prendre deux valeurs : 0 ou 1. La table de vérité de la fonction NOT montre que si l'entrée est dans l'état 0, la sortie se trouve dans l'état 1 et réciproquement, figure 3.
Figure 3. Table de vérité de la fonction NOT Si l'entrée est dans l'état 0, la sortie se trouve dans l'état 1 et réciproquement. |
Revenons maintenant à notre additionneur. Comme nous l'avons vu plus haut, le chiffre correspondant à la somme (\(d_0\)) des deux premiers chiffres binaires est égal à 1 si et seulement si soit \(a_0\) soit \(b_0\) est 1 (pas les deux à la fois). On a donc la table de vérité de la figure 4. La table de vérité comporte maintenant deux entrées \(a_0\) et \(b_0\) et présente toutes les possibilités de combinaisons de ces deux entrées.
La sortie \(d_0\) est 1 si et seulement si soit \(a_0\) soit \(b_0\) est 1 (pas les deux à la fois). Pour les autres combinaisons, la sortie \(d_0\) est 0. |
La fonction logique à laquelle correspond cette table de vérité est la fonction XOR (XOU en français pour OU exclusif).
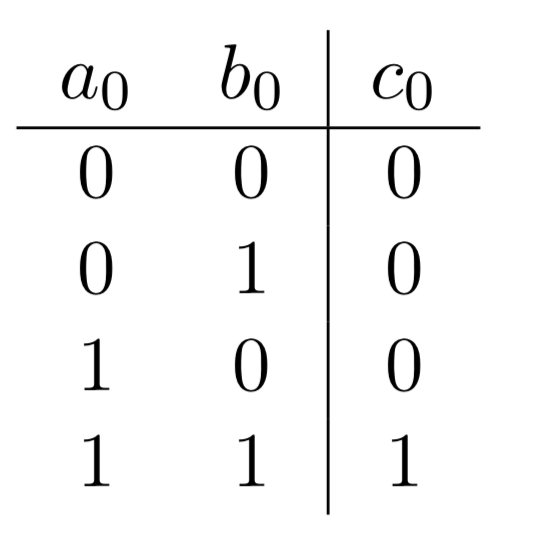
Écrivons maintenant la table de vérité représentant la première retenue (\(c_0\)). Comme nous l'avons vu plus haut, la retenue est égale à 1 si et seulement si \(a_0\) = \(b_0\) = 1. On a donc la table de vérité de la figure 5.
La sortie \(c_0\) est 1 si et seulement si soit \(a_0\) et \(b_0\) = 1. Pour les autres combinaisons, la sortie \(c_0\) est 0. |
La fonction logique à laquelle correspond cette table de vérité est la fonction AND (ET en français).
Finalement, on peut résumer les opérations de la somme et de la retenue de la manière suivante :
\(d_0\) = \(a_0\) XOR \(b_0\)
\(c_0\) = \(a_0\) AND \(b_0\)
2.2 Portes hydrauliques AND et XOR
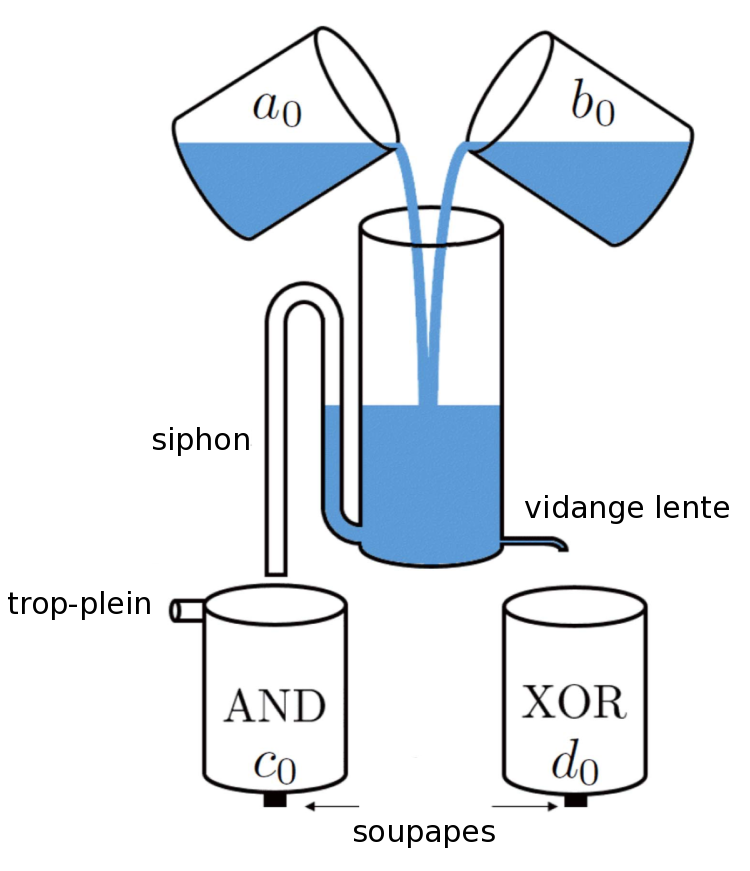
Nous venons de voir que l’addition des chiffres ne requiert que des portes AND et XOR. Le montage hydraulique est présenté sur la figure 6. Il combine ces deux types de portes sur un seul dispositif.
Un récipient central de volume \(V_0\) vient recueillir le contenu simultané de deux pots, plus petits, représentant \(a_0\) et \(b_0\). Si les pots sont vides, ils correspondent à la valeur 0, et s'ils sont plein à la valeur 1. Leur volume est égal à \(V_0/2\).
Un petit trou est percé au bas à droite du récipient principal, annoté « vidange lente », pour permettre à son contenu de sortir lentement. De l’autre côté du récipient central, en bas à gauche, se trouve cette fois un gros trou connecté à un siphon dont la hauteur est supérieure à la moitié du récipient.
Si et seulement si un seul des deux pots est plein (soit \(a_0\) soit \(b_0\)), l’eau versée dans le récipient central va graduellement se vider par la vidange lente dans le pot de droite (\(d_0\)). Par contre, si les deux pots sont pleins, le siphon se retrouve presque instantanément rempli et le contenu du récipient principal s'évacue rapidement dans le pot de gauche (\(c_0\)). Un trop-plein est ajouté dans ce pot afin de s’assurer du bon fonctionnement du calcul binaire.
Notons que même si le siphon est amorcé et l’eau rapidement évacuée du récipient central, il peut rester un peu d’eau qui s’écoule par la vidange lente. Les diamètres de cet orifice et celui du siphon doivent être choisis pour que l’écoulement vers le siphon soit toujours prépondérant.
À l'aide de ce dispositif, les pots fournissent le résultat de l’opération : le pot de droite réalise l’opération XOR et le pot de gauche l’opération AND.
Finalement, les pots en haut et en bas jouent le rôle de mémoire et le récipient central représente les portes logiques.
Il est important de remarquer que les portes logiques présentées ici sont bien une analogie pour présenter du calcul binaire. Il y a une différence fondamentale avec les circuits numériques et le fonctionnement des transistors qui les composent.
2.3 Ajouter n chiffres
Le montage proposé sur la figure 6 permet d’ajouter deux nombres représentés par 1 seul bit (0 ou 1) et renvoie un nombre codé sur 2 bits.
Comme nous l’avons vu plus haut, il peut être utilisé pour calculer la somme des deux premiers chiffres (\(a_0\) et \(b_0\)) d’un nombre. Mais lorsqu’on ajoute deux nombres de plusieurs chiffres (\(a_n\) et \(b_n\)) il faut pouvoir prendre en compte les retenues (\(c_{n-1}\)). Pour créer un additionneur complet nous avons besoin de trois entrées : \(a_n\), \(b_n\) et \(c_{n-1}\) et de deux sorties : \(c_n\) et \(d_n\).
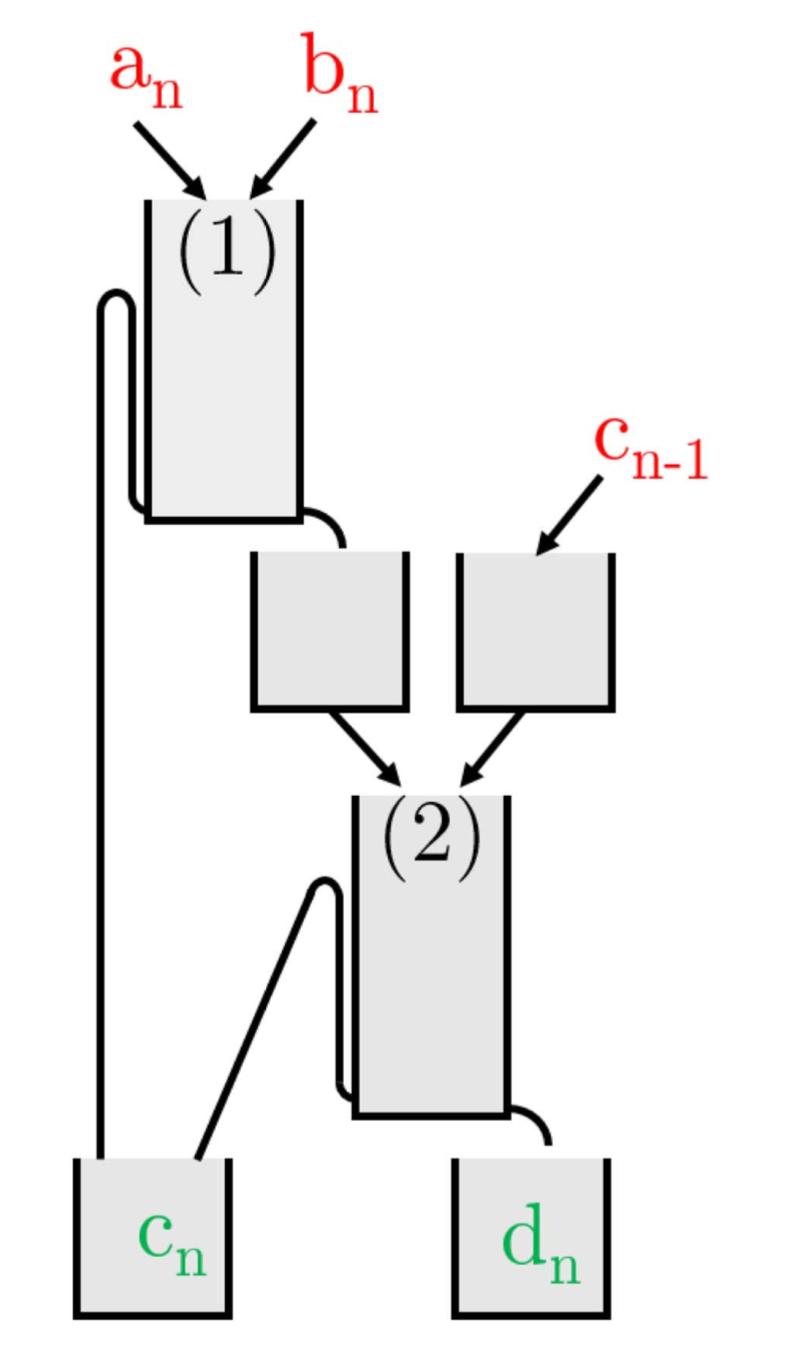
Comme nous l’avons vu avec le premier exemple pour l’addition de 1101 (= 13) avec 1001 (= 9), l’additionneur doit d’abord ajouter les chiffres de même rang ensemble. Leur somme (nième chiffre) obtenue par la fonction XOR doit ensuite être ajoutée à une éventuelle retenue sur le pas précédent (n-1). Cette seconde opération fournit le nième chiffre de la somme (\(d_n\)). Le résultat obtenu par la porte AND renseigne sur la futur retenue. Le montage de l’additionneur complet est présenté sur la figure 7.
Figure 7. Schéma de l'additionneur complet Cet additionneur permet d'ajouter deux chiffres (\(a_n\) et \(b_n\)) et de prendre en compte la retenue (\(c_{n-1}\)) issue du calcul précédent. Le calcul doit être séquencé pour s'assurer que la deuxième opération (2) ne commence qu'une fois que la première (1) est terminée. |
Un point important à surveiller lors du calcul numérique est la capacité à maintenir un très faible taux d’erreur lorsque plusieurs portes logiques sont assemblées en cascade.
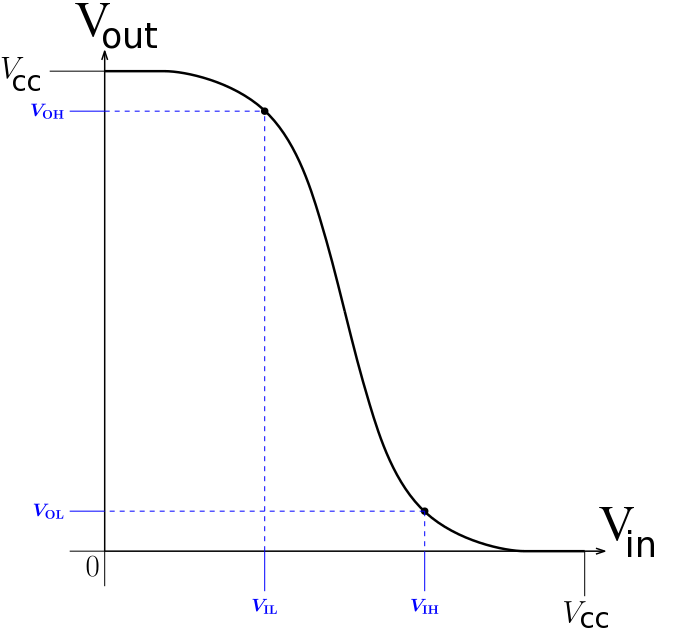
Pour comprendre cela, on peut reprendre l'exemple simple de la porte NOT (NON ou inverseur) qui met en jeu un seul transistor. Dans les circuits logiques, le transistor est utilisé dans un fonctionnement complètement non-linéaire. La fonction de transfert ou courbe de réponse du composant donnant Vout : la tension de sortie, en fonction de Vin la tension d’entrée est présentée figure 8.
Figure 8. Courbe de réponse d'une porte NOT Source : D'après Wikimedia |
Figure 9. Fiche technique du composant SN5405 réalisant la fonction NOT Source : Données tirées d'une datasheet de TI |
Si l'on observe les données constructeurs de la porte NOT donnée en exemple, figure 9, et la courbe de réponse de la porte, on remarque une résistance au bruit (source d'erreur) qui pourrait venir se supperposer au signal. La porte bascule vers une sortie haute VOH (valeur 1) lorsque le signal d'entrée est compris entre 0 V et VIL (pour VIN LOW). De la même manière la porte renvoie une sortie basse VOL (valeur 0) lorsque le signal d'entrée est compris entre VIH (pour VIN HIGH) et VCC (tension d'alimentation de la porte).
Cela permet de lever toute ambiguïté sur la valeur de sortie même si la tension d’entrée peut connaître quelques légères fluctuations.
La réalisation des portes logiques hydrauliques proposée ici est justement aussi basée sur un caractère fortement non-linéaire.
Par exemple, considérons le volume d’eau de la sortie de la porte AND (\(c_0\)) en admettant que le volume d’entrée \(a_0\) est exactement égal à \(V_0\).
Tant que le volume d’eau de l’entrée \(b_0\) est inférieur à \(V_0/2\), le siphon n’est pas enclenché et le volume d’eau dans la sortie est 0. Lorsque le volume devient plus grand que \(V_0/2\), le siphon s’enclenche et et la sortie se remplit très rapidement. Dû à la jauge de trop-plein le volume dans la sortie est exactement \(V_0\). Cette fonction de transfert non-linéaire assure qu’il n’y a pas de propagation d’erreur par le biais de la porte AND.
On peut aussi remarquer que dans la version de l’additionneur proposé ici, il n’y a pas non plus de propagation d’erreur par les portes XOR (pas de propagation de quantité d’eau). En conclusion, le montage proposé ici est robuste aux petites erreurs.
2.4 Fréquence de l'horloge
Lorsqu’on utilise un additionneur complet, il faut faire très attention au temps donné aux opérations. Le premier demi-additionneur (récipient 1 de la figure 7) peut réaliser son calcul dès le début du processus (\(t\) = 0). Mais le deuxième calcul (récipient 2 dans la figure 7 ) doit attendre que toutes les opérations précédentes aient été réalisées. Comme nous l’avons vu plus haut, la sortie de la porte logique AND est obtenue en moins de 5 secondes alors que pour obtenir la sortie de la porte XOR \(T\) = 2 minutes sont nécessaires.
Il faut donc laisser assez de temps avant de commencer les calculs suivants. Ainsi, la seconde opération d’un additionneur complet à \(n\) chiffres doit être réalisé au temps \(t\) = \(n T\).
L’additionneur que nous avons construit fournit une fréquence de calcul de 0,01 Hz, bien en-dessous des fréquences typiques de 1010 Hz des processeurs actuels !
La fréquence de l’horloge de notre additionneur peut être estimée de manière simple. Le temps de vidange le plus long correspond à l'évacuation d'un volume \(V_0\) dans un récipient de diamètre \(D\) à travers un tuyau de diamètre \(d\). D'après la loi de Torricelli si le diamètre \(D\) est plus grand que la longueur capillaire, un temps caractéristique de la vidange peut être donné par :
$$ T=\sqrt{\frac{8 V_0}{\pi D^2 g}} \frac{D^2}{d^2} $$
Où \(g\) est l'accélération de la gravité.
Ainsi, en considérant \(d\) = 700 µm, on obtient \(T\) = 140 s
Il est important de noter que cette fréquence d’horloge ne dépend ni de la viscosité ni de la tension de surface du fluide.
Si l’on garde cette géométrie de l’additionneur, augmenter la fréquence nécessiterait d’augmenter la gravité. Une façon plus pratique d'augmenter la fréquence serait de pressuriser le haut des récipients, mais cela viendrait certainement ajouter d’autres difficultés techniques. Pour des raisons de simplicité, l’additionneur présenté ici ne comprend pas de système de pilotage et repose sur une succession d’ouverture manuelle des valves. On aurait pu aussi le cadencé de manière hydraulique à l'aide de vidanges dont le temps est dont la durée correspond au temps nécessaire pour une opération et avec des système de déplacement de masse qui viennent ouvrir les soupapes.
3. Réalisation pratique
Le récipient central est un tube en plastique de 50 ml, de diamètre \(D\) = 27 mm. Les petits pots (ou unités de mémoire) sont faits avec le même tube mais deux fois moins haut (\(V_0\) = 25 ml).
Le trou correspondant à la vidange lente est percé à l’aide d’une aiguille incandescente et fournit un diamètre \(d\) d’environ 500 microns ± 20%. Le siphon et le trop-plein sont réalisés avec des tuyaux en plastique (5 mm de diamètre).
Avec ce montage, il faut environ 2 minutes pour que le contenu d’un pot (25 ml) se vide lentement dans la porte XOR alors que seulement 5 secondes sont nécessaires pour que le contenu des deux pots (50 ml) s’évacue par le siphon représentant la porte AND. Pour guider l’eau vers la porte XOR un tuyau est collé autour du petit trou. Une soupape réalisée par un petit morceau (5 mm) de caoutchouc est placée au fond de chaque unité de mémoire pour un prochain calcul.
Il faut noter que les effets capillaires peuvent être à la source de différents problèmes : un peu de liquide peut rester piégé dans les tuyaux ou encore l’écoulement par le petit orifice de la vidange lente peut être entravé. Pour surmonter ces problèmes, il est possible de réduire la tension de surface du liquide. Il vaut mieux éviter d'utiliser du savon à cause des bulles ou de la mousse qu’il provoque. Ajouter quelques gouttes d’éthanol dans l’eau permet d’obtenir un bon fonctionnement.
4. Additionneur numérique à 4 bits
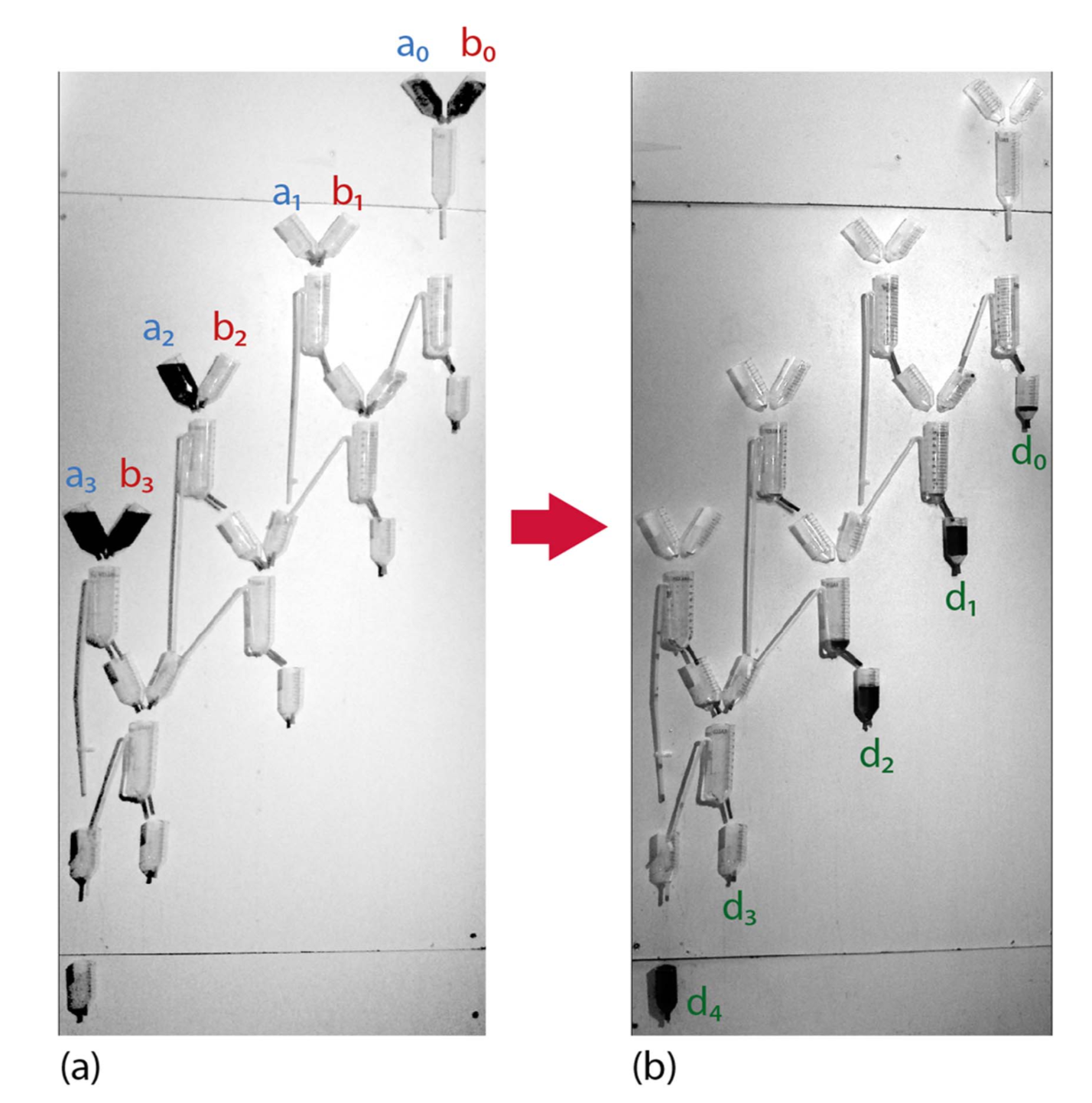
La figure 10 présente un additionneur numérique à 4 bits. Comme nous l’avons vu dans la section 2.3, les unités de mémoire (petits pots) sont vidés dans le récipient central en ôtant un joint en caoutchouc recouvrant un trou de 5 mm placé au fond des pots. Pour plus de visibilité l’eau est colorée en bleu foncé. L’état initial est présenté sur la figure 10a en bleu et rouge
a = 1101 (= 13) et b = 1001 (= 9)
Après 8 minutes, le calcul est terminé et le résultat peut être lu figure 10b, dans les unités de mémoires. En effet, le résultat attendu est bien d = 1011 (= 22).
5. Soustraction
Pour terminer cette présentation de l'additionneur numérique à 4 bits, nous souhaitons montrer qu'il peut aussi être utilisé pour réaliser une soustraction (13 - 9, par exemple). L'idée repose sur l'utilisation d'une méthode connue sous le nom des compléments à deux qui permet d’utiliser des binaires "signés". Le complément à 2 définit le chiffre négatif 9 comme -9 = NOT(9) + 1, auquel par la suite 13 peut être ajouté.
L’opération est présentée dans la table, figure 11.
Figure 11. Calcul de la soustraction : 13 - 9 |
Le résultat ne doit pas être interprété comme un nombre à 5 chiffres, sachant que la différence de deux nombres binaires à 4 chiffres donnera forcément un nombre inférieur à 15.
Par contre, le 5ème chiffre (coloré en orange) renseigne sur le signe. Dans l’exemple donné, figure 11, le résultat 10100 doit être lu comme +4.
L’opération NOT peut être réalisée en utilisant le demi-additionneur présenté dans la section 2.2 sachant que NOT(\(a_n\)) = \(a_n\) XOR 1. On a juste besoin de récupérer le résultat de la porte XOR (vidange lente), le pot b est toujours plein, le résultat de la porte NAND est inutile. L’additionneur 4 bits présenté dans la section 4 pourrait alors être premièrement utilisé pour ajouter 1 à -9, puis être ré-utilisé pour ajouter 13 au résultat !
Pour citer cet article :
TP - Fabrication d'un additionneur numérique hydraulique, Nicolas Taberlet, Quentin Marsal, Jérémy Ferrand, Nicolas Plihon, septembre 2021. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/TP-portes-logiques-hydro.xml