Des électrons vraiment libres ?

Un métal est en première approximation un édifice d'ions positifs ordonnés spatiallement dans un gaz d'électrons libres (modèle proposé par Drude en 1900). Chacun des électrons libres se déplace dans le métal sans être lié à un ion particulier. Ils ont un mouvement aléatoire, une agitation thermique avec une énergie cinétique de l'ordre de kT et subissent des interactions faibles avec les ions et les autres électrons. Ces électrons mobiles sont les électrons de conduction : lorsqu'un champ électrique est appliqué, leur lent déplacement d'ensemble sous l'action de la force électrique constitue le courant électrique, les interactions avec le réseau cristallin étant responsables de la résistivité électrique.

Nous pouvons estimer les forces d'interaction électrostatique et d'interaction gravitationnelle qui s'exercent entre un électron libre et un cation du réseau cristallin, par exemple Cu⁺.

Soit d la distance qui sépare l'électron de masse m_e et de charge électrique q_e = -e d'un cation de masse m_c et de charge électrique q_c. La force d'interaction électrostatique attractive (loi de Coulomb) s'écrit :

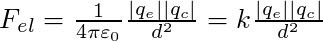
et la force d'interaction gravitationnelle, attractive également (loi de Newton) :

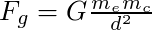
Le rapport de ces deux forces vaut : 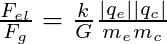et ne dépend pas de la distance électron-cation.

Dans le cas du cuivre, qui possède un électron libre par atome, on considère les interactions entre un électron et un cation Cu⁺ avec 63 nucléons (isotope le plus courant). Avec :

on obtient Fel/Fg = 3,60 x 10³⁷ ! La force d'interaction gravitationnelle électron-cation est complètement négligeable devant la force d'interaction électrostatique entre ces deux espèces chargées.

En considérant que la distance électron libre-cation est approximativement celle de la distance électron-noyau dans l'atome de cuivre isolé, c'est à dire en prenant pour d la valeur du rayon atomique soit 128 pm (d'après la classification périodique des éléments de la Faculty of Chemical Technology, University of Split,Croatia), on estime la valeur de Fel à 1,4 x 10^-8 N.

Calculons maintenant la force d'interaction gravitationnelle entre un électron libre et la Terre, c'est à dire le poids P d'un électron libre. En prenant g = 9,8 N.kg^-1, g étant l'intensité de la pesanteur à la surface de la Terre, on trouve P = m_eg = 8,9 x 10^-30 N, soit 6 x 10^-22 fois moins que Fel.

Bien que très faible, le champ de gravitation agissant sur les électrons libres (et également sur les ions du réseau) modifie (très légèrement) l'organisation d'un solide metallique. Sous l'effet de la pesanteur, le réseau ionique se « tasse » légèrement et les électrons libres se déplacent « vers le bas ». Ce faisant, il se crée des champs électriques induits qui s'opposent aux forces de pesanteur et les compensent. J.-M. Lévy-Leblond et A. Butoli expliquent qu'en faisant l'hypothèse d'un réseau ionique inaffecté, "il suffit pour les électrons de « tomber » de 10^-32 m environ pour être retenus par les ions...".

On peut comparer ce déplacement à la distance interatomique, de l'ordre de 10^-10 m, ou au libre parcours moyen d'un électron de conduction accéléré sous l'effet d'un champ électrique appliqué au métal : dans du cuivre, à température ambiante, ℓ ~ 3 x 10^-8 m. C'est la distance typique parcourue par un électron libre entre deux « collisions » avec des impuretés, des défauts cristallins ou des phonons (mouvements ondulatoires des ions du réseau). On voit que les ordres de grandeurs sont bien différents et que l'effet de la pesanteur est très faible.