Activer le mode zen
Ressource au format PDF
Mots-clés
- tension de surface
- adhérence
- goutte
Classification
Pouvez-vous faire tenir une goutte au plafond ?
06/02/2006
Résumé
Une goutte d'eau sur votre plafond peut-elle ne pas tomber ? Et une goutte d'eau sur une vitre ? Ou sur votre table horizontale ?
Table des matières
Une goutte d'eau sur votre plafond peut-elle ne pas tomber ? Et une goutte d'eau sur une vitre ? Ou sur votre table horizontale ?
Une goutte d'eau sur votre plafond peut-elle ne pas tomber ? Et une goutte d'eau sur une vitre ? Ou sur votre table horizontale ?
Si vous pensez, comme moi, que, oui bien sûr, une goutte d'eau peut tenir sur une table horizontale, prouvez-le !
En effet, appliquons la formule bien connue* donnant la force par unité de longueur s'exerçant sur l'interface entre une goutte de liquide (par exemple de l'eau), un solide (par exemple la table) et l'air :
Ftotale par unité de longueur =γsl +γsg +γlg |
à l'interface liquide-solide est associée la force par unité de longueur γsl, à l'interface solide-gaz la force γsg et à l'interface liquide gaz la force γlg.
* Pour vous rafraîchir la mémoire, vous pouvez allez voir cet article sur les phénomènes d'attraction dus aux forces interfaciales
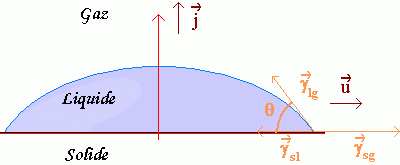
Schéma d'une goutte posée sur une surface horizontale rappelant la direction et le sens de forces interfaciales
Figure 1.
Pour mémoire, si on projette la relation ci-dessus sur le vecteur u, on retrouve l'expression de cos θ en fonction des valeurs des tensions interfactiales.
Mais projetons à présent la relation sur le vecteur vertical j : il nous reste une seule composante : γlg sin θ dirigée vers le haut...
Comment alors la goutte ne "décolle"-t-elle pas de la table?
Si, après réflexion, vous pensez avoir résolu ce problème pour une goutte posée sur une table, penchez-vous sur le cas de la goutte qui serait sur une vitre, ou au plafond... Ces gouttes-là peuvent-elles tenir sur ces surfaces? Savez-vous pourquoi?
La réponse :
On apprend en effet à faire le bilan des forces s'exerçant sur une unité de longueur de la ligne de séparation entre ces trois milieux, et à projeter ce bilan afin de trouver la valeur de l'angle de contact θ de la goutte d'eau avec le solide.

Schéma d'une goutte posée sur une surface horizontale rappelant la direction et le sens des forces interfaciales
Figure 2.
En projetant horizontalement la résultante des forces dessinées sur le schéma ci-dessus, et en écrivant qu'à l'équilibre cette composante horizontale doit être nulle, on trouve - γsl + γsg - γlg cos θ = 0 soit
cos θ = (γsg - γsl)/γlg (relation d'Young) |
Mais que penser de la composante verticale γlg sin θ, non nulle dans le cas général, de la résultante des forces de tension superficielle?
Cette composante verticale est dirigée vers le haut sur ce schéma, et semble tendre à faire "décoller" la goutte du solide sur lequel elle est posée. Pour une goutte suspendue au plafond, elle serait dirigée vers le bas, et semblerait donc tendre là aussi à séparer la goutte du solide.
On pourrait être tenté de croire que cette force est compensée par la gravité, mais :
- on ne pourrait plus invoquer cet argument pour une goutte située au plafond (et une goutte d'humidité au plafond, si son diamètre n'est pas trop important, ne tombe pas nécessairement)
- le calcul de la longueur capillaire (γ/(ρ g))1/2 qui décrit le rapport entre les forces de tension superficielle et l'intensité de la pesanteur (ρ est la masse volumique du liquide) montre que cette-dernière est négligeable devant les effets de tension de surface dès que la goutte d'eau est assez petite, par exemple lorsque son diamètre est de l'ordre du millimètre (cette valeur dépend de la nature des milieux en présence). La gravité ne pourrait donc pas expliquer pourquoi les petites gouttes d'eau ne "décollent" pas de la surface sur laquelle elles sont posées.
En fait, la question "pourquoi la goutte ne décolle-t-elle pas" ne pose problème que parce que l'on ne s'est pas posé un certain nombre de questions essentielles, et tout d'abord, à quoi s'appliquent les forces mises en évidence...
Sur quoi les forces de tension superficielle s'exercent-t-elle?
On dérive généralement l'expression des forces de tension de surface de l'expression de l'énergie γ S associée à une interface de surface S. Le système a tendance à minimiser son énergie donc sa surface. Ce point de vue énergétique équivaut à considérer qu'une force γ, de norme γ, dirigée vers l'intérieur de la surface et tangente à cette-dernière s'exerce sur la limite de l'interface.
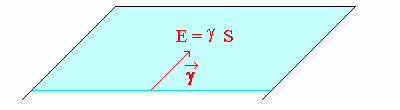
Force de tension superficielle s'exerçant sur l'interface de surface S et d'énergie γ S
Figure 3.
Les forces de tension superficielle dont nous venons de rappeler brièvement l'origine s'appliquent donc à la frontière de l'interface entre deux milieux.
Dans le cas qui nous intéresse, il y a trois forces de tension superficielle qui s'exercent à la frontière de l'interface eau-solide, à la frontière de l'interface eau-air, et à la frontière de l'interface solide-air. Cette frontière est identique pour les trois forces et est la ligne de contact entre l'air, l'eau, et le solide : les forces de tension superficielles décrivent donc une tendance de cette frontière à se déplacer (en l'absence de contrainte supplémentaire) dans la direction déterminée par ces forces.
Ces forces peuvent-elles faire "décoller" cette ligne du solide?
Non, puisque, par définition, cette ligne est la ligne de contact entre les trois milieux, ligne qui appartient à la fois au liquide et au gaz et au solide. La seule façon de voir cette ligne se déplacer vers le haut serait si la surface du solide pouvait se déformer, rendant ainsi un déplacement vertical possible.
Mais, en règle générale, le solide (table, plafond, etc.) "résiste" à la déformation de sa surface : la composante verticale vers le haut de la résultante des forces de tensions superficielle est bien trop faible pour le déformer.
Cette composante verticale ne saurait déterminer une séparation entre la goutte et le solide... Il est possible à une gouttelette d'eau de "tenir" au plafond ou sur une vitre verticale, tout comme sur une surface horizontale. Certes, si les forces de pesanteur deviennent trop importante par rapport aux forces de tension superficielle, la goutte qui se trouve au plafond pourra se décoller. Le calcul de la longueur capillaire pour une surface donnée permet alors de trouver un ordre de grandeur de la taille de goutte au-delà de laquelle les forces de pesanteurs deviennent du même ordre que les forces de tension de surface.
Pour citer cet article :
Pouvez-vous faire tenir une goutte au plafond ?, Gabrielle Bonnet, février 2006. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/QSGoutteDecolle.xml




